机器学习复习＜HENU＞

Chapter1 绪论

基本术语：

监督学习 非监督学习
根据训练数据是否有标记，学习任务可以大致分为监督学习和非监督学习。分类和回归是前者，聚类是后者。

▲何为监督学习、非监督学习？：以西瓜集为例，好瓜坏瓜就是训练集中每一个样本的标记。训练算法过程中通过这个标记不断矫正算法的准确性，这就是监督学习（前面8章学的算法都是监督学习）。反之，训练过程中没有标记的就是非监督学习，比如聚类（就是最后学的k-分类）。

第一章主要是了解一下机器学习大致的东西，了解即可。
学习的种类很多，我们学习监督学习和非监督学习，而二者前者学习的更多，从上面说的章节也可以看出。
监督学习：回归问题、二分类问题
非监督学习：新闻分组等
▲能判断一种算法是监督学习还是非监督学习：

监督学习	非监督学习
线性回归	聚类算法：原型聚类（K均值、学习向量量化、高斯混合聚类）、密度聚类、层次聚类
对数几率回归	降维
决策树	话题分析
支持向量机	图分析
贝叶斯法	/
神经网络	/

机器学习框架：

这个图建议刻画在脑子里

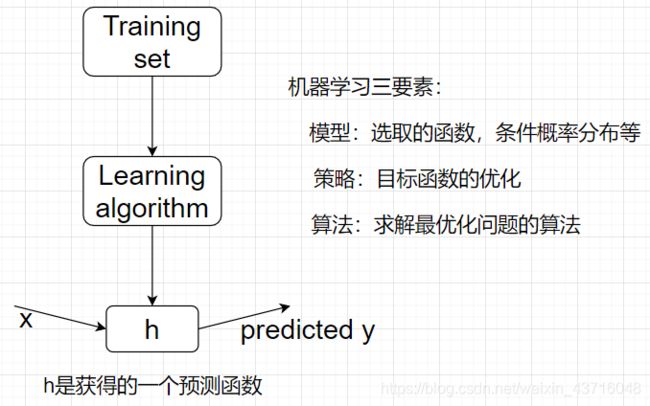
训练集：用来训练算法的样本
测试集：用来测试算法的样本
示例、样例：比如一个题目，给一堆数据集，让你训练一个模型，然后给你一个样例，让你预测一下，这个样例就这个意思
属性、特征；属性值
特征向量：每个样本有很多特征，特征组成一个向量，比如（崔宝,男,18）

训练的目标：学习得到的模型尽可能地适用于新样本。这种适应的能力叫做泛化能力

Chapter2 模型评估与选择

▲怎么评价训练得到的模型的泛化能力：
错误率：分类错误的样本占样本总数的比例
精度：分类正确的样本占样本总数的比例
很明显，错误率+精度=1

---

误差：算法输出值于真实值的差别
_{注意：训练集的所有属性都是已知的，要预测的属性的值也是已知的，比如预测房价，很多因素都会影响房价，如：位置、大小、装修程度等等，想要获得一个预测房价的模型，我们肯定首先知道部分不同位置、不同大小、不同装修程度的房子的价钱，然后基于这些数据来训练模型，预测房价。不清楚的自己找一下ppt看个例子，这个对后面的学习很重要}

训练（经验）误差：训练集上的误差
泛化误差：新样本上的误差

▲训练误差越小越好？
答：不是，如果训练误差越来越小，会导致模型过拟合，则模型不具备很好的泛化能力，则这个模型就差，故训练误差越小越好是错的。

▲泛化误差越小越好
答：是的。我们训练模型的目的就是为了通过模型进行一定的预测，预测的越准确越好，对应的即是泛化误差越小越好。

测试集与训练集应该互斥。互斥即两个集合没有交集。

过拟合：学习到的模型太符合训练集上的特征了。比如说崔宝很丑，结果这个算法认为任何一个男生都很丑。这显然是不合理的。指前半句话
欠拟合：学习到的模型没有把应该考虑进去的属性考虑进去。这个不好举例子，自己体会一下吧

▲减小过拟合的方法：减少特征的数量、数据正则化

▲如果一个模型加入了正则项，这个模型的拟合程度不一定增加。取决于正则化参数入

▲评估模型的方法：掌握交叉验证法（k折交叉验证法）：选择一个k，把数据集分成k份（保持数据分布的一致性），k-1份数据进行训练，剩下一份作测试，一共进行k次，最终取平均值。

留出法：在训练集中选出一部分数据作测试集，注意选择的时候保持数据分布一致性，测试集不能太大不能太小（1/5~1/3）
▲查全率、查准率（课本p30）：

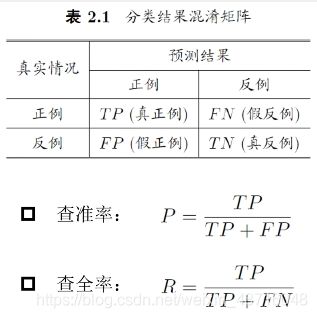
▲查全率查准率的含义：
查准率：预测为正的样本中真正为正的比例
查全率：实际为正的样本中被预测为正的样本的比例
相互矛盾的两个指标

▲均方误差：m个样本求得m个（预测值-真实值）²，相加然后除以m
▲偏差：（预测值-真实值）²。度量了算法预测和真实值的偏离程度，刻画了算法本身的拟合能力
▲方差：度量了同样大小的训练集的变动导致算法性能的变化，刻画了数据扰动带来的影响
偏差和方差度量了和刻画了老师强调了多次。该怎么办不用多说了吧

Chapter3 线性模型

线性模型试图学的一个通过属性的线性组合来进行预测的函数

线性回归

模型的形式f(x) = w1x1+w2x2+…+wdxd+b
向量的形式f(x)=Wx+b

均方误差E(w,b)＝（真实值-预测值） 求和
均方误差后面用的很频繁

优化求解的方法：最小二乘法、梯度下降法

书上给的最小二乘法：通过求导，求极值
▲梯度下降法：

• 三要素：
  假设：先假设一个函数形式，比如f(x)=wx+b
  目标函数：即通过E函数计算损失
  优化算法；给定训练集，如何找到最优参数，使得损失函数最小

▲学习率α对梯度下降的影响：
α如果太小的话，梯度下降算法则会收敛的很慢
α如果太大的话，梯度下降算法则不会收敛，发散或者震荡

对数几率回归

对数几率回归模型：单位跃迁函数数学性质不好，使用对数几率函数替代
解决二分类问题
▲掌握模型的含义:y=P（y=1|x）给出x，估计y=1的可能性

多分类学习:

拆分成若干个二分类求解

拆分策略：
一对多：n个类别，为每一类训练一个罗基分类器，该类作正例，剩下的作为负例，训练分类器的个数n
一对一：n个类别，每次取出两个来训练一个模型。训练分类器的个数n(n-1)/2
多对多：/

Chapter4 决策树

决策树部分不涉及计算题，因为计算过程中牵涉log

划分选择

学习过程：通过对训练样本的分析来确认划分属性。
预测过程：将测试示例从根节点开始，沿着划分属性所构成的”判定测试序列“下行，直到叶结点

▲选择最优划分属性：

• 信息增益:考察这一个
• 增益率
• 基尼指数

▲信息熵：信息熵的值越小，数据集的纯度越高

剪枝处理

剪枝是决策树对付过拟合的主要手段
基本策略：

• 预剪枝：在决策树生成过程中，对每个节点在划分前先进行估计，若当前节点的划分不能带来决策树性能的提升，则停止划分，并将当前节点标记为叶节点
• 后剪枝：先从训练集中生成一颗完整的决策树，然后自底向上对非叶子节点进行考察，若将该节点对应的子树替换为叶子节点能带来决策树泛化性能提升，则将该子树替换为叶节点

预剪枝：提前终止某些分支的生长
后剪枝：生成一颗完全树，再”回头“剪枝
掌握上面的概念

连续的一些概念

连续属性离散化：大于某个数值的作为一类，小于某个数值的作为另外一类
常用二分法
理解连续属性离散化

Chapter5 神经网络

神经元模型

神经网络的概念：很多神经元相连，权重，阈值（偏差）、激活函数
神经网络的学习过程：利用事先提供的训练数据来调整神经元之间的连接权以及每个功能神经元的阈值。

每个神经元都有一个阈值，每条边都有一个权重

感知机与多层网络

感知机
感知机是由两层神经元组成的，输入层和输出层。输入层接受外界信号，输出层输出结果。感知机能够容易地实现或、与、非。
当然，感知机也只能有限的实现这些简单的功能。这些与、或、与、非都是线性问题

感知机要注意了，因为只有输入层输出层，比较简单，会出题。期中测试的时候有一道是感知机的题，通过一些输入输出，让你判断实现了什么功能（与、或、非）
上面这个题老师好像改了，当时激活函数给的好像是sigmoid函数，这里按照sigmoid函数来计算。

怎么实现非线性问题呢？ →多层神经网络
我们学习的都是比较简单的，一般都是三层，即：第一层：输入层、第二层：隐藏层、第三层：输出层

给定一个模型，要会计算有多少个参数

多层神经网络功能比较强大，但是如何得到一个这样的网络呢？→误差逆向传播算法

误差逆向传播算法

即BP算法，基于梯度下降策略。BP算法是一个迭代学习算法，在迭代的每一轮中采用广义的感知机学习规则对参数进行更新估计
不要求掌握公示的推导，不用再愁眉苦脸了。
▲主要掌握BP算法的求解过程，以单隐藏层为例：

1、已知一组数据集（训练集），给定学习率η
2、把所有通过输入层输入获得预测值
3、对于每一个隐藏层到输出层的权重$w_i$，误差E(x)对权重求导，可以得到该权重对误差的影响
4、计算出误差E(x)对所有参数的影响之后，通过更新公式$w_1$ <— $w_1$ - η($\partial L$/$\partial$$w_1$)对所有的参数同时更新
5、迭代3、4，直到满足一定的条件：误差小到一定的程度、达到迭代次数
Tips：更新参数的时候，我记得当时讲的是必须要同时更新，否则如果先更新一部分后，对另外一部分会产生影响。

可以参考另外一篇博客从零训练一个神经网络帮助理解，个人觉得例子比干巴巴的讲理论更加容易理解

BP算法学新能力较强，容易产生过拟合，解决过拟合的办法是：
早停：

• 训练误差连续a轮变化小于b，则停止训练
• 使用验证集，若训练误差降低，经验误差升高，则停止训练

正则化：在误差目标函数中添加一项描述网络复杂度

Chapter6 支持向量机

间隔与支持向量的概念

什么是支持向量？：能够决定最大间隔超平面的点，看ppt或者书上的图可以知道，这些点应该是在正例负例数据的边缘部分，能够决定超平面的选取。后面老师反复讲的那道题给的三个向量就是支持向量，记住就好了， 应付期末考试没问题
什么是间隔？：（正例、负例）支持向量所在的平行面之间的距离就是间隔。γ=2/ ||w|| γ是间隔
上面那个间隔公式怎么来的呢？
有点到平面的距离公式可以得知，正例支持向量到超平面的距离应该是1 / ||w||，负例支持向量应该是|-1| / ||w|| ，两个相加就得到了间隔，即γ=2/ ||w||
掌握点到平面的距离公式:r = |w^Tx+b| / ||w|| （/是除以，markdown分式确实不好写）

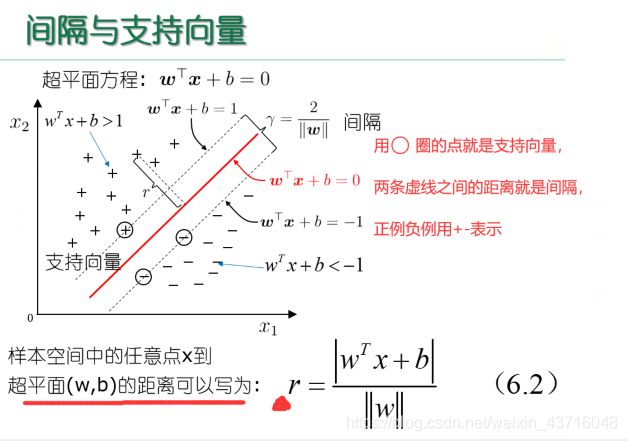
后续的求最大间隔就是求这个γ的值，让其最大。。。
大家应该都知道：求1/n的最大值就是求n的最小值吧？？不知道的话我现在告诉你了，记住就行了。。。。
那求上述的γ的最大值，对应就是求1/γ最小值。这个记好，下面要用

对偶问题

对偶问题必出一道计算题，而且相对较难，建议直接背诵步骤，然后考试直接套上。最下面给出一道例题
求1/γ的最小问题，即arg min $\frac{1}{2}${||w||²}
这里面的公式太多了，我就不手撸了，跟火星文一样太难写了而且理解起来相对较难，我只挑期末考试要用到的说，公式想推导自己可以推导一下。
原问题：arg min $\frac{1}{2}$||w||²
原问题的约束条件是：

▲拉格朗日函数有一下几部分：

• 原函数：即arg min $\frac{1}{2}${||w||²}
• 约束条件的函数：上面那个约束条件，要转化成一个函数≤0的形式，即1-$y_i$(w^T$x_i$+b)<0的形式
• 拉格朗日乘子：${\alpha }_i$，这个很重要，后面就是求这个进而求得w和b的。乘子是非负的，所以接出来的乘子小于零要舍弃，并从区间的端点出取值

拉格朗日函数即：L(w,b,α) = $\frac{1}{2}$||w||²+${\sum }_{i=1}^m$ 1-$y_i$(w^T$x_i$+b)
根据拉格朗日对偶性，原问题的对偶问题就是极大极小问题：
max min L(w,b,α) 其中max是对α，min是对w，b
从内到外求，即先求w，b的极小值，再求α的极大值（其实都是求导，导函数等于0，求得极值）
用L(w,b,α)分别对w，b求导，求出来之后等于0，可以得到
w=${\sum }_{i=1}^m$ ${\alpha }_i{y}_i{X}_i$
0=${\sum }_{i=1}^m$ ${\alpha }_i{y}_i$
上面这两个式子也要记住
得到上面这两个式子之后带入原来的 L(w,b,α)函数得到：
L(w,b,α)=${\sum }_{i=1}^m{\alpha }_i$-$\frac{1}{2}{\sum }_{i=1}^m{\sum }_{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j$
得到这个函数之后，就把给的数据都带进去，然后再求导求出来α。（这里的α是个向量）

---

▲▲▲上面描述了这么多，其实我觉得没有做两道题来的更清楚，下面就基于上述做一下例题：

核函数：用于线性不可分的问题，将样本从原始空间映射到更高维的特征空间，使得样本在这个特征空间内线性可分

正则化

▲清楚$L_p$范数的含义

$L_p$范数是常用的正则化项，其中$L_2$范数$||w|{|}_2$倾向于w的分量取值尽量均衡，即非零个数尽量稠密
而$L_0$范数$||w|{|}_0$和$L_1$范数$||w|{|}_1$则更倾向于w的分量尽量稀疏，即非零分量个数尽量少

• $L_0$范数是指向量中非0的元素的个数
• $L_1$范数是指向量中各元素绝对值 之和
• $L_2$范数是指向量各元素的平方和然后求平方根

Chapter7 贝叶斯分类器

Chapter8 集成学习

Chapter9 聚类