如何从零实现一个神经网络

准备工作

神经元是神经网络必不可少的组成部分，在实现神经网络之前，我们需要先知道什么是神经元

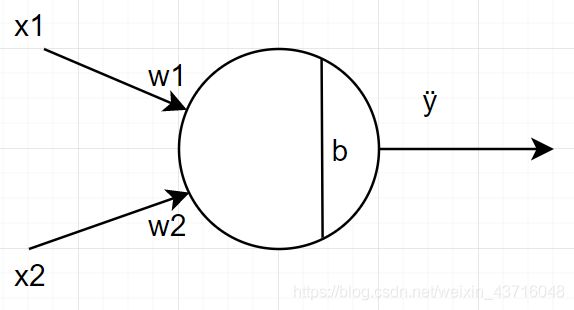
• 神经元是神经网络的基本单元。神经元先获得输入，然后经过一定的数学运算后，产生一个输出。

• 

• 在这个神经元中，有两个输入一个输出，两个输入一共进行了三步运算：
  1、先把两个输入与权重(weights)相乘，：
  x1—>x1*w1
  x2—>x2*w2
  2、把得到的结果相加，再加上偏置(bias)b
  y=x1*w1 + x2*w2 + b
  3、最后经过激活函数处理得到输出
  y=f(x1*w1 + x2*w2 + b)

• 激活函数的作用是将无限制的输入转化为可预测的输出。常用的一个函数是sigmoid函数。
  sigmoid函数的值域在0到1，即在－∞到＋∞中的任意一个输入，经过sigmoid函数之后都可以变成0-1之间的一个数字。

• 基于上述的神经元，我们可以用代码简单实现

# 定义sigmoid函数:f(x)=1/(1+e^(-x))
def sigmoid(x):
    import numpy as np
    return 1/(1+np.exp(-x))

# 定义一个神经元的类
class Neuron:
    def __init__(self, weights, bias):  #传入权重和偏置
        self.weights = weights
        self.bias = bias
    
    def feedforward(self, inputs):     
        total = np.dot(self.weights, inputs)  #数学运算
        return sigmoid(total)   # 返回经过激活函数之后的结果

测试

import numpy as np

weights = np.array([1,0]) 
bias = 2

n = Neuron(weights,bias)   #实例化一个类

test = np.array([3,2])    #创建一个输入

print(n.feedforward(test))   #输出为0.9525741268224334

搭建神经网络

神经网络就是把神经元连接起来，把一个神经元的输出作为下一个神经元的输入。
我们假设这个神经网络中的所有神经元的权重和偏置都是[0,1]、1，激活函数都是sigmoid函数，我们用代码来将这个神经网络表示出来。

class NeuronNetwork:
    def __init__(self):
        weights = np.array([0,1])
        bias = 1
        self.h1 = Neuron(weights,bias)   #h1神经元
        self.h2 = Neuron(weights,bias)   #h2神经元
        self.o1 = Neuron(weights,bias)   #o1神经元
        
    def feedforward(self,x):
        h1 = self.h1.feedforward(x)     #h1神经元的输出
        h2 = self.h2.feedforward(x)     #h2神经元的输出
            
        o1 = self.o1.feedforward([h1,h2])  #o1神经元的输出
            
        return o1

network = NeuronNetwork()

x = np.array([2,3])

print(network.feedforward(x))   #结果为：0.7216325609518421

这样我们就成功的搭建了一个神经网络了，但是这样的输入输出只是为了构建网络，了解他的大致情况，并没有实际意义。

重点

训练神经网络

实际应用中，我们需要神经网络给我们做出合理的预测，即给出一些数据，发现其内在的联系，即根据这些数据，训练出一个神经网络，当有新的数据的时候，可以通过神经网络预测一些我们需要的东西。
比如我们有一个数据集

姓名	身高	体重	性别
a	185	81	男
b	160	48	女
c	178	74	男
d	158	42	女

我们想通过一个人的身高和体重来判断这个人是男是女，那么我们就不能随意的设定权重（weights）和偏置（bais），所以这就需要我们从已经知道的数据出发，找到一个合适的权重和偏置，这样我们就可以通过身高和体重来预测一个人的性别了。

开始

先把数据做一下简答的处理（身高-170，体重-70，1代表男，0代表女）

姓名	身高	体重	性别
a	5	11	1
b	-10	-22	0
c	8	4	1
d	-12	-28	0

我们要有一个标准来定义这个神经网络到底好不好，以便改进。这就是损失（loss）。
一般的，用均方误差来定义损失。

MSE=$\frac{1}{n}$$\sum _{i=1}^n(y_t-y_p{)}^2$

n是样本的数量，从上面可以得知为4
y是预测输出值，即性别，男为1，女为0
$y_t$代表真实的性别，$y_p$代表预测出来的性别
很明显，均方误差越小，预测结果越好。那么我们的目的就是把均方误差降低到最小。将其定义为损失函数。

优化神经网络

使用随机梯度下降的优化算法来训练神经网络。即
$w_1$ <— $w_1$ - η($\partial L$/$\partial$$w_1$)
η是常数，称为学习率，他决定了我们训练网络速率的快慢。这个式子就得到了新的权重$w_1$。
（公式的推导等更新。。。）
训练的流程：
1、从数据集中选择一个样本；
2、计算损失函数对所有权重和偏置的导函数
3、使用更新公式更新每一个权重
4、回到1，直到所有数据集都循环完。
这一步需要用到一定的求偏导的知识，即第2步中计算损失函数对所有权重和偏置的导函数。

import numpy as np

def sigmoid(x):
    return 1/(1+np.exp(-x))

def deriv_sigmoid(x):
    fx = sigmoid(x)
    return fx*(1-fx)

def mse_loss(y_true, y_pred):
    return ((y_true - y_pred)**2).mean()

class NeuralNetwork:
    def __init__(self):
        self.w1 = np.random.normal()
        self.w2 = np.random.normal()        
        self.w3 = np.random.normal()        
        self.w4 = np.random.normal()
        self.w5 = np.random.normal()
        self.w6 = np.random.normal()
        
        self.b1 = np.random.normal()
        self.b2 = np.random.normal()
        self.b3 = np.random.normal()
    def feedforward(self,x):
        h1 = sigmoid(self.w1*x[0] + self.w2*x[1] + self.b1)
        h2 = sigmoid(self.w3*x[0] + self.w4*x[1] + self.b2)
        o1 = sigmoid(self.w5*h1 + self.w6*h2 + self.b3)
        
        return o1
    def train(self, data, all_y_trues):
        
        learn_rate = 0.1
        epochs = 500
        for epochs in range(epochs):
            for x, y_true in zip(data,all_y_trues):
                sum_h1 = self.w1*x[0] + self.w2*x[1] + self.b1
                h1 = sigmoid(sum_h1)
            
                sum_h2 = self.w3*x[0] + self.w4*x[1] + self.b2
                h2 = sigmoid(sum_h2)
            
                sum_o1 = self.w4*h1 + self.w5*h2 + self.b3
                o1 = sigmoid(sum_o1)
                y_pred = o1
            
                d_L_d_y_pred = -2 * (y_true - y_pred)
            
                d_ypred_d_w5 = h1*deriv_sigmoid(sum_o1)
                d_ypred_d_w6 = h2*deriv_sigmoid(sum_o1)
                d_ypred_d_b3 = deriv_sigmoid(sum_o1)
            
                d_ypred_d_h1 = self.w5*deriv_sigmoid(sum_o1)
                d_ypred_d_h2 = self.w6*deriv_sigmoid(sum_o1)
            
                d_h1_d_w1 = x[0]*deriv_sigmoid(sum_h1)
                d_h1_d_w2 = x[1]*deriv_sigmoid(sum_h1)
                d_h1_d_b1 = deriv_sigmoid(sum_h1)
            
                d_h2_d_w3 = x[0]*deriv_sigmoid(sum_h2)
                d_h2_d_w4 = x[1]*deriv_sigmoid(sum_h2)
                d_h2_d_b2 = deriv_sigmoid(sum_h2)
            
                self.w1 -= learn_rate*d_L_d_y_pred*d_ypred_d_h1*d_h1_d_w1
                self.w2 -= learn_rate*d_L_d_y_pred*d_ypred_d_h1*d_h1_d_w2
                self.b1 -= learn_rate*d_L_d_y_pred*d_ypred_d_h1*d_h1_d_b1
                
                self.w3 -= learn_rate*d_L_d_y_pred*d_ypred_d_h2*d_h2_d_w3
                self.w4 -= learn_rate*d_L_d_y_pred*d_ypred_d_h2*d_h2_d_w4
                self.b2 -= learn_rate*d_L_d_y_pred*d_ypred_d_h2*d_h2_d_b2
            
                self.w5 -= learn_rate*d_L_d_y_pred*d_ypred_d_w5
                self.w6 -= learn_rate*d_L_d_y_pred*d_ypred_d_w6
                self.b3 -= learn_rate*d_L_d_y_pred*d_ypred_d_b3

训练神经网络由于时间问题来不及一下更新完，会挤时间时间更新