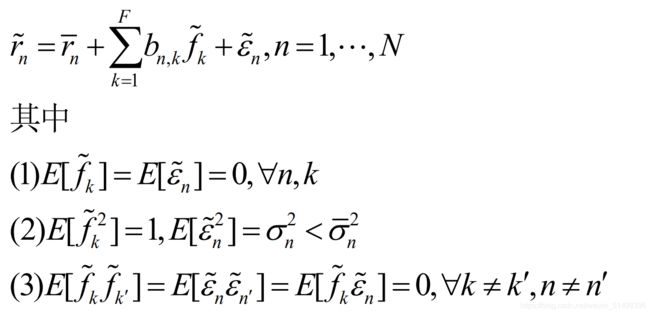金融经济学(王江)期末梳理第十四章 APT定价理论
套利定价理论
- Introduction
- 两种思想的区别(博迪)
- 14.1 线性因子模型
-
- 14.1.1 模型结构
- 14.1.2 模型解释
- 14.1.3 记号
- 14.2 精确因子模型
-
- 14.2.1 单因子模型: r ~ n = r ‾ n + b n f ~ \tilde r_n=\overline r_n+ b_n\tilde f r~n=rn+bnf~
-
- 1、存在一个无风险组合和一个因子载荷为1的组合
-
- (1)构建组合
- (2)无风险组合
- (3)定义λ
- (4)因子组合
- 2、单因子模型
-
- (1)理论: r ‾ n = r F + b n λ \overline r_n=r_F+b_nλ rn=rF+bnλ
- (2)理解:
- (3)与CAPM关系:
- (4)实证分析**:计量经济学估计组合的期望收益率
- 14.2.2 精确F因子模型: r ~ = r ‾ l + b f ~ \tilde r=\overline rl+b\tilde f r~=rl+bf~ 其中E f ~ = 0 \tilde f=0 f~=0
-
- 1 套利组合
- 2 F因子模型 r ‾ = λ 0 l + ∑ k b k λ k \overline r=λ_0l+\sum_kb_kλ_k r=λ0l+∑kbkλk
- 14.3 极限套利(统计套利)
-
- 14.3.1 基本思想
-
- 1、极限套利机会
- 2、APT定价理论适用条件
-
- 两个条件
-
- 一个条件:不存在极限套利机会
- 14.3.2 无极限套利和无套利
- 14.1 作为均衡结果的APT
-
- 定理:均衡结果
Introduction
CAPM依赖于均值-方差假设将证券风险分解为两部分有溢价的市场风险和无溢价的剩余风险,虽然依赖于偏好或支付的强条件,但是这种风险结构的分解具有普遍的经济意义,这一章将摒弃偏好的假设,直接从风险结构出发,基于无套利假设,提出套利定价理论(Ross)
两种思想的区别(博迪)
均值-方差框架中,当均衡价格被打破时,投资者将在一定程度上改变他们的投资组合,这取决于他们的风险厌恶程度。这些有限的投资组合改变的加总会产生大量的买卖行为,从而重建均衡价格。
在无套利原理中,当套利机会存在时,每个投资者都愿意尽可能多的持有头寸,因此不需要很多投资者就会使价格恢复平衡,显然后者更具有经济意义。
14.1 线性因子模型
14.1.1 模型结构
14.1.2 模型解释
套利定价理论将证券的收益率分为三个部分:
第一部分期望收益率 r ‾ n = E [ r ~ n ] \overline r_n=E[\tilde r_n] rn=E[r~n]
第二部分是其主要观点:资产收益率由F个共同风险因子决定,即反映了系统风险,每个风险因子前的系数 b k b_k bk表示第k个因子风险的大小,因此也叫第k个风险因子的载荷,共同因子无多重共线性。
第三部分是与共同风险因子无关的剩余风险 ε n \varepsilon_n εn,并且假定各种资产的剩余风险因子是不相关的,否则就是共同因子,剩余风险的协方差阵为对角阵。
特别的,只有当因子F 为了记号的方便,我们用 r ~ \tilde r r~表示收益率向量(N维向量) r ‾ \overline r r为期望收益率向量。 f ~ \tilde f f~为风险因子向量(F维向量)b为因子载荷矩阵(N×F) 那么可以把上述因子模型写成向量模式: r ~ = r ‾ + b f ~ + ε ~ \tilde r=\overline r+b\tilde f+\tilde \varepsilon r~=r+bf~+ε~ (2) E [ f ~ f ~ ′ ] = I , E [ ε ~ ε ~ ′ ] = ∑ E[\tilde f\tilde f']=I,E[\tilde\varepsilon \tilde\varepsilon']=\sum E[f~f~′]=I,E[ε~ε~′]=∑(因子方差为1,特殊风险为对角阵) (3) E [ f ~ ε ~ ′ ] = 0 E[\tilde f\tilde \varepsilon']=0 E[f~ε~′]=0 (无相关) 我们先考虑不存在剩余风险的情况,证明是线性因子。 证明:假设由两个资产i和j,并且对于单因子模型中的载荷 b i ≠ b j b_i \not=b_j bi=bj且均不为0. 考虑两个资产构成的组合** r ~ p = w r ~ i + ( 1 − w ) r ~ j \tilde r_p=w\tilde r_i+(1-w)\tilde r_j r~p=wr~i+(1−w)r~j 其中 r ~ i = r ‾ i + b i f ~ \tilde r_i=\overline r_i +b_i\tilde f r~i=ri+bif~ , r ~ j = r ‾ j + b j f ~ \tilde r_j=\overline r_j+b_j\tilde f r~j=rj+bjf~ 所以 r ~ p = w ( r ‾ i + b i f ~ ) + ( 1 − w ) ( r ‾ j + b j f ~ ) \tilde r_p=w(\overline r_i +b_i\tilde f)+(1-w)(\overline r_j+b_j\tilde f) r~p=w(ri+bif~)+(1−w)(rj+bjf~) = w r ‾ i + ( 1 − w ) r ‾ j + [ w b i + ( 1 − w ) b j ] f =w\overline r_i+(1-w)\overline r_j+[wb_i+(1-w)b_j]f =wri+(1−w)rj+[wbi+(1−w)bj]f 取 w b i + ( 1 − w ) b j = 0 wb_i+(1-w)b_j=0 wbi+(1−w)bj=0**, 则无风险组合 r ~ 0 = w r ‾ i + ( 1 − w ) r ‾ j \tilde r_0=w\overline r_i+(1-w)\overline r_j r~0=wri+(1−w)rj 其中w= b j b j − b i b_j\over b_j-b_i bj−bibj,带入上式有 r ~ 0 = \tilde r_0= r~0= b j b j − b i b_j\over b_j-b_i bj−bibj r ‾ i − \overline r_i- ri− b j b j − b i b_j\over b_j-b_i bj−bibj r ‾ j = r F \overline r_j=r_F rj=rF r ‾ j − r F b j \overline r_j-r_F\over bj bjrj−rF= r ‾ i − r F b i \overline r_i-r_F\over bi biri−rF= r ‾ j − r i b j − b i \overline r_j-r_i\over b_j-b_i bj−birj−ri=λ**,所以不论资产为什么都有这个关系。 具有单位因子得组合也叫做因子组合,选择w使得因子载荷为1 即 w b i + ( 1 − w ) b j = 1 wb_i+(1-w)b_j=1 wbi+(1−w)bj=1**, 得w= 1 − b j b i − b j 1-b_j\over b_i-b_j bi−bj1−bj 带入原式有 r ~ 1 = \tilde r_1= r~1= 1 − b j b i − b j 1-b_j\over b_i-b_j bi−bj1−bj r ‾ i − \overline r_i- ri− 1 − b i b i − b j 1-b_i\over b_i-b_j bi−bj1−bi r ‾ j \overline r_j rj+ f ~ \tilde f f~= r ‾ i − r ‾ j b i − b j \overline r_i-\overline r_j\over b_i-b_j bi−bjri−rj+ b i r ‾ j − b j r ‾ i b i − b j b_i\overline r_j-b_j\overline r_i\over b_i-b_j bi−bjbirj−bjri= λ + r F λ+r_F λ+rF+ f ~ \tilde f f~ 两边同时取期望: 即用因子组合的风险溢价替代了因子的影响。 1、可以用无套利原理证明:相同的因子载荷具有相同的超额回报率,因为对于所有资产因子价格都是因子组合的溢价。 我们得到了因子组合后,取与证券n风险特征相同的一个组合 b n b_n bn单位的因子组合和1- b n b_n bn单位的无风险证券,那么未来支付为 组合: b n ( 1 + r ~ 1 ) + ( 1 − b n ) ( 1 + r F ) = b n ( 1 + λ + r F b_n(1+\tilde r_1)+(1-b_n)(1+r_F)=b_n(1+λ+r_F bn(1+r~1)+(1−bn)(1+rF)=bn(1+λ+rF+ f ~ ) \tilde f) f~) + ( 1 − b n ) ( 1 + r F ) = ( 1 + r F ) + b n λ + b n f ~ +(1-b_n)(1+r_F)=(1+r_F)+b_nλ+b_n\tilde f +(1−bn)(1+rF)=(1+rF)+bnλ+bnf~ 证券n:1+ r ~ n = 1 + r ‾ n + b n f ~ \tilde r_n=1+\overline r_n+ b_n\tilde f r~n=1+rn+bnf~ 两者收益相等: r ‾ n = r F + b n λ \overline r_n=r_F+b_nλ rn=rF+bnλ 所以因子用λ替代,是线性的。 2、可以用λ恒等式证明: r ‾ j − r F b j \overline r_j-r_F\over bj bjrj−rF= r ‾ i − r F b i \overline r_i-r_F\over bi biri−rF= r ‾ j − r i b j − b i \overline r_j-r_i\over b_j-b_i bj−birj−ri=λ 那么对于任意资产n有: r ‾ n = r F + b n λ \overline r_n=r_F+b_nλ rn=rF+bnλ (1) 由因子组合 λ = r ‾ 1 − r F λ=\overline r_1-r_F λ=r1−rF r ‾ n = r F + b n ( r ‾ 1 − r F ) \overline r_n=r_F+b_n(\overline r_1-r_F) rn=rF+bn(r1−rF) 这样我们就得到了一个结论: 任意资产的风险溢价取决于它负载的因子风险。因子风险大小由因子载荷度量,其中因子载荷为1的风险溢价λ为因子风险的价格,所以风险溢价为bλ,这就是单因子模型下的套利定价理论。 式(1)基于无套利原理:如果存在一个资产n,不满足(1)式,假设 r ‾ n > r F + b n λ \overline r_n>r_F+b_nλ rn>rF+bnλ r ‾ n = r F + b n λ \overline r_n=r_F+b_nλ rn=rF+bnλ 对因子组合 r ~ 1 = λ + r F \tilde r_1=λ+r_F r~1=λ+rF+ f ~ \tilde f f~两边取期望得到 λ= r ‾ 1 − r F \overline r_1-r_F r1−rF将其带入单因子模型 r ‾ n − r F = b n ( r ‾ 1 − r F ) \overline r_n-r_F=b_n(\overline r_1-r_F) rn−rF=bn(r1−rF) 当因子是市场超额收益率时,单因子模型和CAPM具有相同的形式。 计算一个组合的期望收益 需要知道,β,无风险利率,市场组合的期望收益所以CAPM要估计市场组合收益(N个证券的期望收益率),β(N个收益率的方差,N(N-1)/2个协方差) 单因子模型: r ~ n = r ‾ n + b n f ~ + ε n \tilde r_n=\overline r_n+ b_n\tilde f+\varepsilon_n r~n=rn+bnf~+εn 收益率的方差为: σ i 2 = b n 2 σ f 2 + σ 2 ( ε n ) σ_i^2=b_n^2σ_f^2+ σ^2(\varepsilon_n) σi2=bn2σf2+σ2(εn) 显然在单因子模型下参数大大优化了(主要是对β的估计) 考虑一个套利组合z, z T l = 0 z^Tl=0 zTl=0,根据无套利原理,其期望收益也应该为0.如果 z T b = 0 z^Tb=0 zTb=0,显然有 z T r ~ = 0 z^T\tilde r=0 zTr~=0,如果组合的载荷为0,那么组合收益率也为0. 假设: r ~ = r ‾ + b f ~ \tilde r=\overline r+b\tilde f r~=r+bf~ 其中E f ~ = 0 \tilde f=0 f~=0 给定收益的F因子模型,根据无套利原理有 r ‾ = λ 0 l + ∑ k b k λ k \overline r=λ_0l+\sum_kb_kλ_k r=λ0l+∑kbkλk, 其中k表示第k个因子。 证明:任意 { z : z T l = 0 , z T b = 0 , k = 1 , 2 , … , F } \{z: z^Tl=0,z^Tb=0,k=1,2,…,F\} { z:zTl=0,zTb=0,k=1,2,…,F} 意味着 z T r ~ = 0 z^T\tilde r=0 zTr~=0,即零成本和零风险因子的组合期望收益也为0.否则就可以套利 所以 r ‾ \overline r r与 l 和 b 共 线 l和b共线 l和b共线,即线性表出,可以写成 r ‾ = λ 0 l + ∑ k b k λ k \overline r=λ_0l+\sum_kb_kλ_k r=λ0l+∑kbkλk 如果至少有F+1个资产的收益率是线性无关的,那么上述定理成立,也就是说存在无风险证券和F个因子组合且 λ 0 = r F λ_0=r_F λ0=rF。 事实上,对于F个风险因子,可以构造F个因子组合,求出对应的λ。 在精确因子模型中,我们可以用F个因子和无风险证券来复制其他资产的收益,从而由无套利原理得到APT定价关系。 极限套利:如果因子的个数远小于资产的个数,那么我们可以使用多个资产构造组合以分散每个资产的特殊风险,如果特殊风险被分散的足够小,那么资产组合几乎只有因子风险,那么我们的精确因子模型就可以应用了。 给定资产 n = 1 , 2 … n=1,2… n=1,2…由前n个资产构成套利组合序列 z n z^n zn,下面n都表示序列,而不是次数. 剩余风险有界、不存在极限套利机会。 而 λ 0 + b i λ λ_0+biλ λ0+biλ为精确因子模型定价关系 两者相减类似残差平方和的意思,上式的意思就是使残差平方和小于某个值,即使得n趋于无穷大时,所有资产的定价误差有限。 证明: 0,且与共同风险不相关。我们要证明n→∞时, Q ( n ) = η ( n ) T η ( n ) < A Q^{(n)}=\eta^{(n)T}\eta^{(n)}Q(n)=η(n)Tη(n)<A. step2:反证法 假设n→∞时, Q ( n ) = η ( n ) T η ( n ) → ∞ Q^{(n)}=\eta^{(n)T}\eta^{(n)}→∞ Q(n)=η(n)Tη(n)→∞,同样找到一个因子风险和成本为0的组合,证明其支付大于0即可。 考虑套利组合 z ( n ) = h ( n ) η ( n ) z^{(n)}=h^{(n)}\eta^{(n)} z(n)=h(n)η(n),使得 h ( n ) η ( n ) l = 0 h^{(n)}\eta^{(n)}l=0 h(n)η(n)l=0; h ( n ) η ( n ) b ( n ) = 0 h^{(n)}\eta^{(n)}b^{(n)}=0 h(n)η(n)b(n)=0 step4:求组合的期望收益和方差 E [ h ( n ) η ( n ) T r ~ ( n ) ] = h ( n ) η ( n ) T r ‾ ( n ) E[h^{(n)}\eta^{(n)T}\tilde r^{(n)}]=h^{(n)}\eta^{(n)T}\overline r^{(n)} E[h(n)η(n)Tr~(n)]=h(n)η(n)Tr(n) 将初始条件带入 (2)方差: V a r [ h ( n ) η ( n ) T r ~ ( n ) ] = V a r [ h ( n ) η ( n ) T e ~ ( n ) ] = ( h ( n ) ) 2 η ( n ) T ∑ η ( n ) Var[h^{(n)}\eta^{(n)T}\tilde r^{(n)}]=Var[h^{(n)}\eta^{(n)T}\tilde e^{(n)}]= (h^{(n)})^2\eta^{(n)T}\sum\eta^{(n)} Var[h(n)η(n)Tr~(n)]=Var[h(n)η(n)Te~(n)]=(h(n))2η(n)T∑η(n) = ( h ( n ) ) 2 ∑ i σ i 2 η i 2 < σ ‾ 2 ( h ( n ) ) 2 ∑ i η i 2 =(h^{(n)})^2\sum_i\sigma_i^2\eta_i^2<\overline \sigma^2(h^{(n)})^2\sum_i\eta_i^2 =(h(n))2∑iσi2ηi2<σ2(h(n))2∑iηi2 = σ ‾ 2 ( h ( n ) ) 2 η ( n ) T η ( n ) = σ ‾ 2 ( h ( n ) ) 2 Q ( n ) =\overline\sigma^2(h^{(n)})^2\eta^{(n)T}\eta^{(n)}=\overline\sigma^2(h^{(n)})^2Q^{(n)} =σ2(h(n))2η(n)Tη(n)=σ2(h(n))2Q(n) 其中 ( ∑ ) n = σ n 2 < σ ‾ 2 (\sum)_n=\sigma_n^2<\overline \sigma^2 (∑)n=σn2<σ2即剩余风险有限,而且是对角阵 (3)取 h ( n ) = ( Q ( n ) ) ( − 2 / 3 ) h^{(n)}=(Q^{(n)})^{(-2/3)} h(n)=(Q(n))(−2/3): E = h ( n ) Q ( n ) = ( Q ( n ) ) ( 1 / 3 ) → ∞ E=h^{(n)}Q^{(n)}=(Q^{(n)})^{(1/3)}→∞ E=h(n)Q(n)=(Q(n))(1/3)→∞ V a r = σ ‾ 2 ( h ( n ) ) 2 Q ( n ) = ( Q ( n ) ) ( − 1 / 3 ) → 0 Var =\overline\sigma^2(h^{(n)})^2Q^{(n)}=(Q^{(n)})^{(-1/3)}→0 Var=σ2(h(n))2Q(n)=(Q(n))(−1/3)→0 显然,这是一个极限套利组合,所以假设不成立。 这是只有少部分资产APT是无效的。 无套利是均衡条件,而无极限套利则不是均衡条件(实际上包含着对偏好的假定如常数绝对风险厌恶的负指数效用函数)类似前面正态分布求解过程(与书上答案不同?)解出价格向量之后,即可计算收益率,发现收益率只与残差项有关,即只有剩余风险,但是其收益率显著不为0,显然违反了APT套利定价理论。 APT只是近似的定价效果:在不存在极限套利机会时,效果较好。这一部分对经济结构进行限制后,APT套利定价关系是一般均衡的结果。 市场结构:1只无风险证券和N只风险证券,证券市场具有因子结构,其中有一个是无风险证券:即支付因子载荷为0。 x ~ = x ‾ + b x f ~ + ε ~ \tilde x=\overline x +b_x\tilde f +\tilde \varepsilon x~=x+bxf~+ε~ E [ ε ∣ f ~ ] = 0 E[\varepsilon|\tilde f]=0 E[ε∣f~]=0, 独立 6条假设下,APT是均衡的结果:14.1.3 记号
其中:
(1) E [ f ~ ] = E [ ε ~ ] = 0 E[\tilde f]=E[\tilde \varepsilon]=0 E[f~]=E[ε~]=0 (回归到均值收益率)14.2 精确因子模型
14.2.1 单因子模型: r ~ n = r ‾ n + b n f ~ \tilde r_n=\overline r_n+ b_n\tilde f r~n=rn+bnf~
1、存在一个无风险组合和一个因子载荷为1的组合
(1)构建组合
(2)无风险组合
(3)定义λ
(4)因子组合
r ‾ 1 = λ + r F \overline r_1=λ+r_F r1=λ+rF则 λ = r ‾ 1 − r F λ=\overline r_1-r_F λ=r1−rF2、单因子模型
(1)理论: r ‾ n = r F + b n λ \overline r_n=r_F+b_nλ rn=rF+bnλ
具有单位因子得组合也叫做因子组合,它的风险溢价λ叫做因子溢价,也就是风险因子得风险价格。下面我们看λ定义式:(2)理解:
考虑套利组合:买入一单位资产n,卖出 b n b_n bn单位因子组合以及1- b n b_n bn单位无风险资产。(初始投资为0)未来支付为
r ‾ n − b n ( λ + r F ) − ( 1 − b n ) r F = r ‾ n − b n λ − r F > 0 \overline r_n-b_n(λ+r_F)-(1-b_n)r_F=\overline r_n-b_nλ-r_F>0 rn−bn(λ+rF)−(1−bn)rF=rn−bnλ−rF>0
这是一个套利机会。因此如果不存在套利机会,(1)式必须成立。(3)与CAPM关系:
(4)实证分析**:计量经济学估计组合的期望收益率
1、因子的期望也需要估计1
2、估计市场收益率需要: N个证券的期望收益率
3、估计协差阵需要:N个b,N个残差方差,1因子方差。估计β,
协方差被简化: C o v ( r i , r j ) = b i b j σ f 2 Cov(r_i,r_j)=b_ib_jσ_f^2 Cov(ri,rj)=bibjσf214.2.2 精确F因子模型: r ~ = r ‾ l + b f ~ \tilde r=\overline rl+b\tilde f r~=rl+bf~ 其中E f ~ = 0 \tilde f=0 f~=0
1 套利组合
2 F因子模型 r ‾ = λ 0 l + ∑ k b k λ k \overline r=λ_0l+\sum_kb_kλ_k r=λ0l+∑kbkλk
14.3 极限套利(统计套利)
在一般因子模型中,F个因子只能复制一个资产的因子风险,不能消除或复制特殊风险即非系统性风险,所以通过无套利原理,无法达到严格的套利定价关系,此时,我们必须考虑极限套利,过去时间涨得慢的股票,未来可能涨的快。14.3.1 基本思想
1、极限套利机会
当n→∞时,有 ( z n ) T r ‾ n → δ > 0 且 V a r [ ( z n ) T r ~ n ] → 0 (z^n)^T\overline r^n→\delta>0且Var[(z^n)^T\tilde r^n]→0 (zn)Trn→δ>0且Var[(zn)Tr~n]→0
即具有平稳的收益率序列,向均值回归于一个正常数,则称这个套利组合序列为极限套利机会。2、APT定价理论适用条件
两个条件

解释:
其中 r ‾ i \overline r_i ri时,资产i的真实期望收益率
step1:问题描述
假设存在剩余风险,则有:n个证券,F个因子
根据,剩余风险假定,有 η ( n ) T l = 0 , η ( n ) T b ( n ) = 0 \eta^{(n)T}l=0, \eta^{(n)T}b^{(n)}=0 η(n)Tl=0,η(n)Tb(n)=0即剩余风险期望为
step3: 寻找零因子风险和零成本的组合
(1)期望:
有: E [ h ( n ) η ( n ) T r ~ ( n ) ] = h ( n ) η ( n ) T E[h^{(n)}\eta^{(n)T}\tilde r^{(n)}]=h^{(n)}\eta^{(n)T} E[h(n)η(n)Tr~(n)]=h(n)η(n)T r ‾ ( n ) = h ( n ) η ( n ) T η ( n ) = h ( n ) Q ( n ) \overline r^{(n)}=h^{(n)}\eta^{(n)T}\eta^{(n)}=h^{(n)}Q^{(n)} r(n)=h(n)η(n)Tη(n)=h(n)Q(n)一个条件:不存在极限套利机会
14.3.2 无极限套利和无套利
另一方面:建立与无风险头寸相反的风险头寸即成本为0但是组合期望和方差满足极限套利组合,说明存在极限套利机会。(简单解释为其风险厌恶系数不变,无论财富多少,对风险溢价的要求相同,反映在市场上会使得证券的价值偏高)14.1 作为均衡结果的APT
定理:均衡结果
(1)证券支付具有因子结构,且其中存在无风险证券,0因子载荷
(2)每个因子都可由证券支付线性表出
(3)参与者的1期消费可由证券支付线性表出
(4)参与者的1期总禀赋可由因子线性表出
(5)参与者是严格厌恶风险的
(6)均衡配置是内部解
类似CAPM 10个假设,了解即可