LeetCode初级算法之数组:预测买卖股票的最佳时机II
题目描述:
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
初步思路
这个题拿到之后,没有想那么多,直接考虑局部最大化,即假如我发现后面一天比当前股票的价格高,那我就买,这就是买的时间。 而啥时候卖呢? 买的前提是后面一天的价格比当前价格高,当天买, 那我后一天就卖吗? 不是,我判断了一下后一天的后一天,如果还大,那么我就一直往后找,直到一个波峰的位置我才卖,这时候,肯定保证了这只股票赚的局部最大。所以初步代码如下:
class Solution {
public:
int maxProfit(vector<int>& prices) {
int maxprofit = 0; // 统计最高的利润,也就是最后的返回值
int days = prices.size();
int stock[days+1];
// 把向量中的数存放到数组中,便于后面的操作
vector <int> ::iterator it;
int cou = 0;
for (it=prices.begin(); it!=prices.end(); it++)
{
stock[cou++] = *it;
}
// 接下来遍历数组
int saletime, buytime;
int p, q;
buytime = 0; //第一天的股票价格
while (buytime<days-1)
{
p = buytime+1;
if (p<days && stock[p]<=stock[buytime]) //股票价格下跌,此时不买前面那个,buytime后移
{
buytime++;
}
else if(p<days) //此时,股票价格上涨,要往后找到涨的最高峰,这个时候是最佳卖的时间
{
q = p+1;
while (q<days && stock[q]>stock[p])
{
p = q;
q = q + 1;
}
if (q<=days) // 找到了涨的最高峰,p指向了,这时候,就是最佳卖出去的时候
{
saletime = p;
maxprofit += (stock[saletime]-stock[buytime]);
buytime = q;
}
}
}
return maxprofit;
}
};
// 测试代码
int main()
{
int arr[] = {
7, 6, 4, 3, 1};
vector<int> price(arr, arr+5);
Solution s;
cout << s.maxProfit(price);
return 0;
}
于是就遍历一遍数组,让buytime指向当前数组的第一个位置,在buytime小于最后一个位置的时候,遍历,p指向buytime的下一个元素,
- 如果p小于buytime位置的元素,那么就是后一天比前一天价格少,股票跌了,那么我就不买,buytime指针后移。 然后再重复上面。
- 但是如果p大于buytime位置的元素,那么说明股票价格涨了,我就想办法找到涨的最高的位置(因为p后面还可能一直涨),怎么做呢? 于是一个指针q指向p后面的位置,然后判断是否大于p位置的元素,如果大于,那么p,q交替移动,往后找涨的最后位置(类似于找最长子序列),如果发现q比p的元素小了, 那么卖的时间就是p,saletime指向,然后计算出这时候的利润,stock[saletime]-stock[buytime]。然后buytime指向q, 重复上面的过程即可。
改进思路1 - 峰谷思路
上面的思路原来是一种波峰波谷的思路,类似这样,假设给定的数组为:[7, 1, 5, 3, 6, 4], 如果我们在图表上绘制给定数组中的数字,我们将会得到
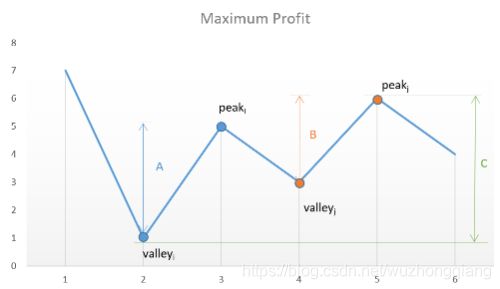
看这个图就一目了然了,上面我求的,就是波谷-波峰,所有的加和,
数学表达如下:
![]()
PS: 我们需要考虑到紧跟谷的每一个峰值以最大化利润。如果我们试图跳过其中一个峰值来获取更多利润,那么我们最终将失去其中一笔交易中获得的利润,从而导致总利润的降低。(例如,在上述情况下,如果我们跳过 peak_i 和 valley_j,试图通过考虑差异较大的点以获取更多的利润,获得的净利润总是会小与包含它们而获得的静利润,因为 C 总是小于 A+B。)
简化的代码如下:
class Solution {
public:
int maxProfit(vector<int>& prices) {
int days = prices.size();
int stock[days+1];
//cout << days << endl;
// 把向量中的数存放到数组中,便于后面的操作
vector <int> ::iterator it;
int cou = 0;
for (it=prices.begin(); it!=prices.end(); it++)
{
stock[cou++] = *it;
}
// for (int i=0; i
// cout << stock[i] << " ";
// cout << endl;
// 接下来遍历数组
int saleprice = stock[0];
int buyprice = stock[0];
int maxprofit = 0; // 统计最高的利润,也就是最后的返回值
int i = 0;
while (i<days-1)
{
while (i<days-1 && stock[i]>=stock[i+1])
i++;
buyprice = stock[i];
while (i<days-1 && stock[i]<=stock[i+1])
i++;
saleprice = stock[i];
maxprofit += (saleprice-buyprice);
}
return maxprofit;
}
};
这个其实和我第一次的思路一样,只不过是代码写的更加简洁了。
时间复杂度 O(n) 遍历一次
空间复杂度O(n) 因为又重新开辟了空间存放数组,C++里面没法获取直接获取数组的长度,所以形参还是用vector,然后又存了一遍,有点麻烦。
改进思路2 - 贪心思路
该解决方案遵循峰谷思路的解题逻辑,但是有一些轻微的变换。 这种情况下,我们可以简单的继续在斜坡上并持续增加从连续交易中获得的利润,而不是在谷之后寻找每个峰值。 因为题目中可以当天买,当天卖,那么我就可以每天连续的买卖,只要后一天的价格比当前的价格大,那我就买,后一天接着卖, 依次往后推,我只考虑这个局部最优,这样我肯定保证稳赚不赔。
数学表示:
就是把那个连续上涨的那段给拆开:

看下图可能更加形象些:
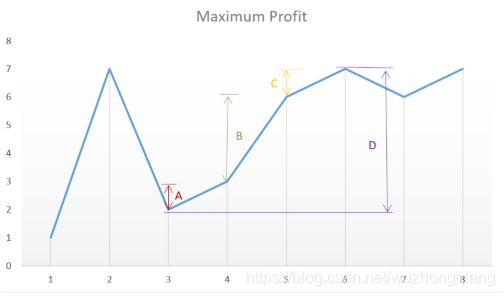
如果后一个数比前一个数大,那么我们就可以尽可能的获得其中的利润。在A处买入,B处值比A大,抛出获得(B-A)的利润,C处值比B大,所以B处买入C处抛出,以此类推,直到D点,分段卖卖的利润和谷买峰卖的利润是相同的,从而避免了峰值和谷值的循环查找。而且代码也很简洁。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int days = prices.size();
int stock[days+1];
//cout << days << endl;
// 把向量中的数存放到数组中,便于后面的操作
vector <int> ::iterator it;
int cou = 0;
for (it=prices.begin(); it!=prices.end(); it++)
{
stock[cou++] = *it;
}
int maxprofit = 0;
// 接下来遍历数组
for (int i=1; i<days; i++)
{
if (stock[i]>stock[i-1])
maxprofit += (stock[i]-stock[i-1]);
}
return maxprofit;
}
};
这个代码是比较简洁的,速度也很快,目前发现的最好的思路了吧。
总结
这个题可能容易陷入的思考误区就是不知道如何确定买卖的时间。
比如[7, 1, 5, 6] 第二天买入,第四天卖出,收益最大(6-1),所以一般人可能会想,怎么判断不是第三天就卖出了呢?
这里就把问题复杂化了,根据题目的意思,当天卖出以后,当天还可以买入,所以其实可以第三天卖出,第三天买入,第四天又卖出((5-1)+ (6-5) === 6 - 1)。所以算法可以直接简化为只要今天比昨天大,就卖出。
所以有时候,不要先考虑全局最优,找最佳的,可以先尝试的采用贪心的策略,每一步去找个最优的,说不定到了最后就是最好的。
PS:
我发现LeetCode上,用C++写代码,数组部分,形参需要使用一个动态的向量先存,然后再往一个数组中写,再操作,有些麻烦,但是目前没有找到比较好的办法,因为如果直接把形参改成数组的时候,不知道数组的长度。
所以,找了一些C++获取数组长度的方式和向量的知识:
- c++中计算数组的长度。以及c++中向量的长度的计算的方式。
- c++ vector数组的使用