第二章 Python NLP实战-核心技术与算法----中文分词技术

---

前言

自然语言中每句话都由若干个词语组成，相较于英文而言，中文的分词显然难上许多。中文的词语之间没有像英文的空格一样的标记符来区分词语，此外，中文词语的开放性也使得中文分词很难有一个统一的标准，如何提高分词的正确率，已成为当下研究的一个焦点。

这篇博客将会介绍迄今为止一些主流的分词算法及相关的代码实现。文章较长，请按需阅读。废话不多说，以下是本篇文章正文内容。

---

一、中文分词的痛点

1.1 中文的歧义性

举两个例子，例如在这句话中“南京市长江大桥”，我们即可划分为“南京市/长江大桥”，也可划分为“南京/市长/江/大桥”。又或者是这样一句话：“羽毛球拍卖光了”，即可划分为“羽毛球拍/卖/光了”，也可以划分为“羽毛球/拍卖/光了”。很显然，在没有具体语境的情况下，两种划分都是可行的。这就给中文分词的歧义消除带来了很大的麻烦。

1.2 识别未登录词

首先介绍一下什么是未登录词，未登陆词是指没有收录到词典中的词。传统的分词方法都是基于规则的匹配分词方法。首先会有一个收录了大量词语的中文词典，然后利用正向匹配或是逆向匹配算法进行词语划分。但是随着人们语言的需要，新的词组接连不断的出现在语料中。如果未登录词没有出现在词典中，就会导致错分或者漏分，使得最终的分词准确率大大降低。因此，未登录词识别是提高分词效率的重点之一。

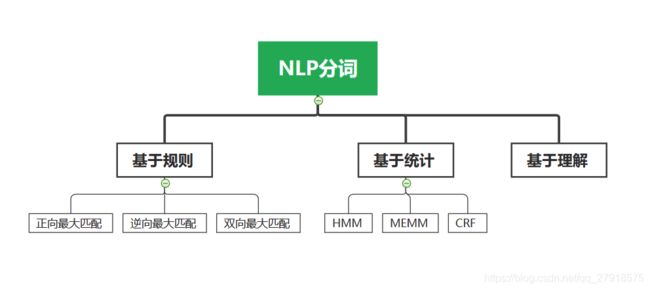
二、基于规则的分词算法

在中文分词中，通过将待分词的句子与词典中的词语进行逐一匹配，进而将句子划分为多个词的分词方法，我们称之为基于规则的分词方法（或基于词典的分词方法、机械分词方法）。

2.1 切分方式

按照匹配词语的切分方式，主要可以分为正向匹配法、逆向匹配法以及双向匹配法。

2.1.1 正向匹配法

顾名思义，正向匹配法就是按照句子的正向序列，从句子的第一个字符开始，逐一进行匹配。正向匹配法中，以正向最大匹配法（Maximum Match Method，MM法）最为典型。其基本思想为：假设分词词典中的最长词有i个字符，则利用被处理句子中的前i个字作为匹配字段，查找字典。若字典中存在这样的词，则匹配成功，匹配字段被切分出来；若不匹配，则将匹配字段的最后一个字去掉，重新进行匹配，重复下去，直到匹配成功，即切分出一个词或剩下的长度为0为止，这样就完成了一轮匹配。然后取下一个长度为i的字符串进行匹配处理，直到文档被扫描完为止。

2.1.2 逆向匹配法

同理，逆向匹配法就是从句子的最后一个字符开始，逐一进行匹配。由于汉语中偏正结构较多，若从后向前匹配，可以适当的提高京都。所以逆向最大匹配法（Reverse Maximun Match Method）比正向最大匹配法的误差要小一点。

2.1.3 双向匹配法

双向最大匹配法（Bi-direction Match Method）则是结合了正向和逆向匹配，选取其中匹配结果串数目少的作为最终的匹配结果。当然，值得注意的是， 当匹配结果切分串数目相同时，则选取切分串中，单字最少的为最终结果。

话不多说，下面是简单的demo演示：

# 正向最大匹配算法
class MM(object):
    def __init__(self):
        self.window_size = 4

    def search(self,text,dic):
        result = []
        index = 0
        text_length = len(text)
        while text_length > index:
            for size in range (self.window_size + index , index , -1) :
                piece = text[index:size]
                if piece in dic:
                    index=size-1
                    break
            index = index +1
            result.append(piece)
        return result

# 逆向最大匹配算法
class RMM(object):
    def __init__(self):
        self.window_size = 4

    def search(self,text,dic):
        result=[]
        index = len(text)
        text_length = len(text)
        while index > 0 :
            for size in range(index-self.window_size,index,1):
                piece = text[size:index]
                if piece in dic :
                    index = size + 1
                    break
            index = index - 1
            result.append(piece)
        result.reverse()
        return result

#双向最大匹配法
class  BiMM(object):
    def __init__(self):
        self.mm = MM()
        self.rmm = RMM()

    def search(self,text,dic):
        result = []
        temp1 = self.mm.search(text,dic)
        temp2 = self.rmm.search(text,dic)
        if len(temp1)>len(temp2):
            result = temp2
        elif len(temp1) len_single_temp2:
                    result = temp2
                else:
                    result = temp1
        return result





if __name__ == '__main__':
        text1 = '南京市长江大桥'
        text2 = '研究生命的起源'
        dic = ['南京市', '长江大桥', '南京', '市长', '江', '大桥','研究','研究生','生命','命','的','起源']

        tokenizerMM = MM()
        tokenizerRMM = RMM()
        tokenizerBiMM = BiMM()
        print('token : 南京市长江大桥')
        print('MM : ')
        print(tokenizerMM.search(text1,dic))
        print('RMM : ')
        print(tokenizerRMM.search(text1, dic))
        print('BiMM : ')
        print(tokenizerBiMM.search(text1,dic))
        print('----------------------------')
        print('token : 研究生命的起源')
        print('MM : ')
        print(tokenizerMM.search(text2, dic))
        print('RMM : ')
        print(tokenizerRMM.search(text2, dic))
        print('BiMM : ')
        print(tokenizerBiMM.search(text2, dic))

下面是算法的执行结果：

token : 南京市长江大桥
MM : 
['南京市', '长江大桥']
RMM : 
['南京市', '长江大桥']
BiMM : 
['南京市', '长江大桥']
----------------------------
token : 研究生命的起源
MM : 
['研究生', '命', '的', '起源']
RMM : 
['研究', '生命', '的', '起源']
BiMM : 
['研究', '生命', '的', '起源']

研究表明，99%的中文句子在使用匹配算法进行切分时，必定有一个是正确的，只有不到1%的切分结果是错误的。这也正是双向匹配算法在中文信息处理系统中得以广泛应用的原因。

2.2 词典机制

机械的分词算法中第二个重点就是词典机制。词典的结构机制会直接影响到基于词典的分词算法的匹配效率。为了提高分词效率，设计一个‘优秀’的词典机制是十分重要的。当然建立一个‘优秀’的词典，也不是一件容易的事。下面简单介绍一下部分研究成果。

清华大学孙茂松教授等通过实验对比了整词二分，Trie索引术及逐字二分这3种典型的分词词典机制，结果表明，基于逐字二分的分词词典机制是一种简洁、高效的词典阻止模式；李庆虎等在3种典型的词典基础上，提出一种双字哈希的词典机制，进一步提高了自动分词的时间效率。赵欢等提出了一种改进的双数组Trie索引树分词算法。莫建文等对中文分词词典的双字哈希结构及最大匹配算法进行改进，在一定程度上增加了正向最大匹配的正确率。此外，在词典中建立词长度索引表也可以大大减少匹配次数，提高了分词效率。

词典是中文分词不可或缺的一部分。尽管经过学者的不断完善和改进，提高了分词的效率。但是，单独依赖现有的词典，在各个领域上进行分词明显存在缺陷，尤其是歧义消除和未登录词的识别问题难以得到解决。

---

三、基于统计的分词算法

随着大规模语料库的建立，统计机器学习方法的研究和发展，基于统计的中文分词算法开始逐渐成为主流。

首先介绍一下何为基于统计的分词算法。在中文句子中，虽然没有任何的分词标记符，但是词由汉字组成，相邻的汉字或者相邻的词能否组合成词，可以利用相邻汉字在语料库中出现的频率来计算概率，作为判断的依据。基于统计的分词算法通过训练大量已经过人工分词的语料库获取经验信息，建立一个能反映响铃汉字间互信度的概率模型，从而来识别词并进行词语的划分。

这里介绍两种经典的基于统计的分词模型和其代码实现：

3.1 HMM（Hidden Markov Model，隐马尔可夫模型）

3.1.1 HMM概念及推导

隐马尔可夫模型是一种具有隐含状态的马尔可夫模型，它是相较于马尔可夫模型来说的。我们将句子中的每一个单词作一个隐含状态划分，其隐含状态集合为O，包含4种隐藏状态信息（O：{B,M,E,S}，其中B表示词首，M表示词中，E表示词尾，S表示单独成词）。比如有如下句子：“我爱自然语言处理”，我们标记出其隐含状态则是：“我/S 爱/S 自/B 然/M 语/M 言/M 处/M 理/E”。如果在统计学角度来看这个问题，用数学抽象表示如下：用$\lambda ={\lambda }_1{\lambda }_2...{\lambda }_n$来表示输入的句子，n为句子的长度，${\lambda }_i$表示第i个字，$o=o_1{o}_2...o_n$表示输出状态序列，那么理想的输出就是：$$max=maxP(o_1{o}_2...o_n|{\lambda }_1{\lambda }_2...{\lambda }_n)$$，其表示在句子序列为$\lambda$时，最有可能的输出序列$o$。则通过这个语言模型，原问题则转化为求max$P(o|\lambda )$的问题。

需要注意的是，$P(o|\lambda )$是关于2n个变量的条件概率，且n是不固定的，因此，几乎无法进行精确计算。此时我们引入贝叶斯公式：将P进行如下变换：$$P(o|\lambda )=\frac{P(o,\lambda )}{P(\lambda )}=\frac{P(\lambda |o)P(o)}{P(\lambda )}$$其中：
          $P(o,\lambda )$为联合概率，即状态$o$和$\lambda$同时出现的概率；

          $P(\lambda )$为句子$\lambda$在语料库中出现的概率，我们可以用频率代替概率，可以看做是常量；

所以：原公式则转换为求：$$P(\lambda |o)P(o)$$

这里，我们针对$P(\lambda |o)$作观测独立性假设得到：$$P(\lambda |o)=P({\lambda }_1|o_1)P({\lambda }_2|o_2)...P({\lambda }_n|o_n)$$

同时，针对$P(o)$作齐次马尔科夫假设：t时刻的状态o，仅与其前一个状态有关，于是得到：$$P(o)=P(o_1)P(o_2|o_1)P(o_3|o_2)...P(o_n|o_{n-1})$$
代入原式得到HMM模型：$$P(\lambda |o)P(o)=P({\lambda }_1|o_1)P({\lambda }_2|o_2)...P({\lambda }_n|o_n)P(o_1)P(o_2|o_1)P(o_3|o_2)...P(o_n|o_{n-1})$$
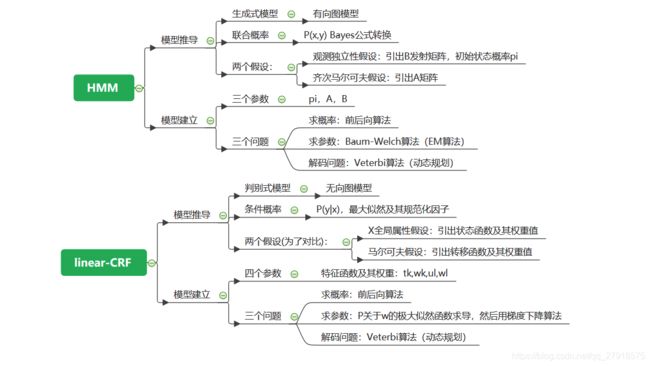
在HMM模型中，将$P({\lambda }_k|o_k)$称谓发射概率，由发射概率组成的矩阵称为发射矩阵，我们用B来表示；将$P(o_k|o_{k-1})$称为状态转移概率，其组成的矩阵为状态转移矩阵，我们用A来表示；$P(o_1)$我们称之为初始状态概率，由$\pi$来表示；由此，我们的HMM模型则可以表示为：HMM = $\lambda (\pi ,A,B)$，其中三个系数分别为初始状态概率，状态转移概率矩阵，发射概率矩阵。值得说的是，HMM模型为二元语言模型，也就是我们在求解$P(o)$时采用的是齐次马尔科夫假设，也就是t 时刻的状态$o_i$仅仅与其前一个状态$o_{i-1}$有关；若将这里假设换为：t 时刻的状态$o_i$与其前两个状态$o_{i-1}和o_{i-2}$有关，则产生的语言模型为三元语言模型；同理，若t 时刻的状态$o_i$与其前n个状态都有关系（或者说前i个状态，这里用n代替），则得到n元语言模型，也就是我们常说的n-gram模型。

3.1.2 HMM求解中文分词问题

经过上面的推导，我们知道HMM的三个参数分别为$\lambda (\pi ,A,B)$，如果我们将句子中的文字看作是观测序列，将句子中每个字的词位置符号序列看作是隐藏状态序列，则分词问题可以化为已知观测序列，求其最大概率的状态序列，可以用隐马尔科夫模型求解。求解步骤一般分为三个步骤：

（1）训练：利用语料库，训练HMM的三个参数。

（2）预测：已知观测序列$\lambda$和已经训练好的HMM，求解其最大概率的状态序列$o$。

（3）分词：利用状态序列$o$，对原句子进行词语划分。

下面我们对每一个步骤进行相关算法的解释和代码实现。

3.1.2.1 训练

在训练阶段，我们利用语料库中的大量的中文文本信息，进行HMM的训练，最终的到HMM的三个参数 $\lambda (\pi ,A,B)$。

HMM的参数求解可以分为两种，第一种：已知D个长度为N的观测序列和其对应的隐藏状态序列，即$\{({\lambda }_1,o_1),({\lambda }_2,o_2)...({\lambda }_D,o_D)\}$是已知的。我们可以很容易的用最大似然法来求解模型参数，即利用频率来代替概率。但是很多时候我们只能得到语料库中的对应的观测序列 $\lambda$ ，并不能得到其对应的隐藏状态序列$o$。这就是第二种情况：已知$\{({\lambda }_1),({\lambda }_2)...({\lambda }_D)\}$，求解HMM参数问题。这里就需要用到Baum-Welch算法（鲍姆-韦尔奇算法），其实也就是基于EM算法的求解。

Baum-Welch算法详细推导笔记：请移步刘建平老师的博文：
隐马尔科夫模型HMM（三）鲍姆-韦尔奇算法求解HMM参数

Baum-Welch算法流程（注意这里的观测序列和隐含状态变量叫法和上面的不同）：
（1）确定输入输出：观测序列 $O$ ,及其隐含状态 $I$ （状态未知），求模型参数$\pi ，A，B$；
（2）随机初始化参数$\pi ，A，B$，注意初始化的时候必须满足其概率分布；
（3）EM算法的E步：针对固定的参数$\pi ，A，B$，求 $O,I$ 联合分布条件概率期望；
（4）EM算法的M步：对于其条件概率期望求极大值。因为其期望表达式为$\pi$，$a_{ij}$ ，$b_{j}k$的函数，所以分别对其函数表达式求极大值则得到对应的$\pi$，$a_{ij}$ ，$b_{j}k$。
（5）判断$\pi$，$a_{ij}$ ，$b_{j}k$是否收敛，若收敛，则退出；否则重复第三步；

3.1.2.2 预测

在预测阶段，利用已经建模好的HMM模型，对每一个输入的观测序列O，输出其隐藏状态序列。即已知$\lambda (\pi ,A,B)$和O，求$I$。常用的求解方法时Veterbi（维特比）算法。它时一种动态规划方法，其核心思想是：如果最终的最优路径经过某个$o_i$，那么从初始节点到$o_{i-1}$的路径也是最优路径，因为每个节点只会影响前后两个$P(o_{i-1}|o_i)$和$P(o_i|o_{i+1})$。（请区分动态规划和贪心的概念，不要混淆）

Veterbi算法详细推导笔记：请移步刘建平老师的博文：
隐马尔科夫模型HMM（四）维特比算法解码隐藏状态序列

Veterbi算法流程：
（1）初始化$t_0$时刻的局部状态：$${\delta }_1(i)={\pi }_i{b}_i(o_1)，i=1,2...N$$ $${\psi }_1(i)=0，i=1,2...N$$其中：${\delta }_1(i)$为该时刻的隐藏状态概率函数，以其最大值为局部最优解；${\psi }_1(i)$为隐藏状态记录函数，记录局部最优解所选用的隐藏状态信息。

（2）进行动态规划递推时刻$t=1,2,...T$时刻的局部状态，并记录每个局部状态的最优路径选择的节点，记录为：$${\delta }_t(i)=b_i(o_t)ma{x}_{1\le j\le N}[{\delta }_{t-1}(j)a_{ji}]，i=1,2...N$$ $${\psi }_t(i)=argma{x}_{1\le j\le N}[{\delta }_{t-1}(j)a_{ji}]，i=1,2...N$$

（3）计算最终时刻T最大的${\delta }_T(i)$值作为最可能的隐藏状态序列出现的概率。计算T时刻最大的$\psi (i)$，即为T时刻最可能的隐藏状态；

（4）利用T时刻的隐藏状态$\psi (i)$开始回溯，对于$t=T-1,T-2,...,1$；$$i_t^{\ast }={\psi }_{t+1}(i_{t+1}^{\ast })$$

（5）最终得到最有可能的隐藏状态序列$I$。$$I^{\ast }=\{i_1^{\ast },i_2^{\ast },...i_T^{\ast }\}$$

值得注意的是：Veterbi算法是利用动态规划算法的思想来求解全最短路径问题，即将隐藏序列$I$看作一个整体，先求$P(I|O)$的最大值，然后再利用记录函数 $\psi$ 来回溯所经过的节点。这与基于贪心算法的求解过程是有区别的。

3.1.2.3 分词

在分词阶段，经过Veterbi算法，我们已经得到了观测序列$O$对应的隐藏状态序列 $I$，分词阶段的任务则是利用 $I$ 对句子进行划分。一般情况下，我们使用从左到右的最大匹配模式进行词语划分，这个比较简单，这里就不再赘述。

3.1.3 HMM代码实践

暂无

3.2 CRF（Conditional Randow Field，条件随机场）

3.2.1 CRF的概念及推导

要理解条件随机场，首先我们得理解什么是随机场。

随机场：是由若干个位置组成的整体，当给每一个位置中按照某种分布随机赋予一个值后，其全体就叫做随机场。

马尔可夫随机场：某个位置的值仅仅与其相邻位置的值有关，（即一前一后），与其他位置都没有关系，这样的随机场叫做马尔可夫随机场。

条件随机场：只有两种变量$X,Y$，则称条件概率$P(X|Y)$为条件随机场。以分词为例：变量$X$为给定的观测序列$O$,变量$Y$则表示对应的隐藏状态$(S,M,B,E)$。
对于CRF，我们给出准确的数学语言描述则是：设X与Y是随机变量，$P(Y|X)$是给定X时Y的条件概率分布，若随机变量Y构成的是一个马尔科夫随机场，则称条件概率分布$P(Y|X)$是条件随机场。

线性链条件随机场（linear-CRF）：CRF的定义中，并没有指定X和Y必须具有相同的结构，而现实中，我们一般都假设X和Y具有相同的结构，即$$X=(X_1,X_2,...,X_n)$$ $$Y=(Y_1,Y_2,...,Y_n)$$于是得出线性链条件随机场的定义：
设$X=(X_1,X_2,...,X_n)$,$Y=(Y_1,Y_2,...,Y_n)$均为线性链表示的随机变量序列，在给定随机变量序列X的情况下，随机变量Y的条件概率分布$P(Y|X)$构成条件随机场，即满足马尔科夫性：
$P(Y_i|X,Y_1,Y_2,...Y_n)=P(Y_i|X,Y_{i-1},Y_{i+1})$，则称$P(Y|X)$为线性链条件随机场。

CRF推导：
首先我们来看看HMM和CRF的结构图：

不难发现，HMM的结构是一个有向图，其节点之间的变换我们可以由HMM中的参数A来表示转换概率，而且同一时间 $t$ 内，Y与X之间的映射我们可以由HMM中的参数B来表示发射概率。

在CRF结构图中，节点之间构成一个无向图。当前节点的状态不仅于前一个状态有关，而且与其后一个状态也有关系，这个时候我们仅仅使用状态转移概率矩阵是不能表示无向图的结构特性的。于是我们利用一系列的状态转移函数来表示 $t$ 时刻的节点与 $t-1$时刻节点之间的转移关系，这一系列的转移函数，我们用$t_k(y_{i-1},y_i,i),k=1,2,...K$(K为转移函数数目)来表示。同理，对于HMM模型中的发射矩阵B，我们也用一组状态函数$s_l(y_i,X,i),l=1,2,...,L$(L为状态函数的数目)，注意这里的X没有写作$x_i$，其原因是因为CRF中的状态函数是一组具有全局性质的函数，这与作观测独立性假设的HMM有所不同。 我们统称这两种函数为CRF特征函数。特征函数的取值为1或者0，表示符不符合该条规则的约束，同时，我们对每一个特征函数定义其权重值$w_i$，表示对这个特征函数的信任程度。假设$t_k$的权重为${\lambda }_k$，$s_l$的权重为${\mu }_l$，则CRF模型由所有的$t_k,{\lambda }_k,s_l,{\mu }_l$共同决定。

在HMM模型中，我们求解$P(Y|X)$是将它看做联合概率分布，即$P(Y,X)$,并且利用贝叶斯公式进行转换，然后针对转换后的公式做观测独立性假设和一阶马尔可夫假设（齐次马尔可夫假设）。但是在CRF模型中，我们将Y与X之间的分布看作条件概率分布$P(Y|X)$，对无向图进行建模，模型参数为$t_k,{\lambda }_k,s_l,{\mu }_l$，最后我们得到的CRF参数化形式如下：

$$P(y|x)=\frac{1}{Z(x)}exp(\sum _{i,k}{\lambda }_k{t}_k(y_{i-1},y_i,i)+\sum _{i,l}{\mu }_l{s}_l(y_i,X,i))$$

其中：$$Z(x)=\sum _{y}exp(\sum _{i,k}{\lambda }_k{t}_k(y_{i-1},y_i,i)+\sum _{i,l}{\mu }_l{s}_l(y_i,X,i))$$Z(x)为规范化因子，其求和操作是在所有可能的输出序列上做的。

由于上式比较复杂，因为转移函数和状态函数其本质都是特征函数，所以将其表达式和权重系数用一个统一函数来表示：则简化后的CRF表示为：$$P(y|x)=\frac{1}{Z(x)}exp(\sum _j\sum _i{w}_j{f}_j(y_{i-1},y_i,x,i))$$其规范化因子Z(x)为：$$Z(x)=\sum _{y}exp(\sum _j\sum _i{w}_j{f}_j(y_{i-1},y_i,x,i))$$其中：$f_j(y_{i-1},y_i,x,i)$为特征函数的统一表示，其展开为为：$$f_j(y_{i-1},y_i,x,i)={\{}_{s_l(y_i,X,i)j=K+1,K+2,...,K+L}^{t_k(y_{i-1},y_i,i)j=1,2,...,K}$$ $w_j$为权重的统一表示，其展开为：$$w_j={\{}_{{\mu }_{l}j=K+1,K+2,...,K+L}^{{\lambda }_{k}j=1,2,...,K}$$

3.2.2 CRF求解中文分词问题

同样的，在利用CRF求解中文分词问题时，也于无监督的HMM模型一样，需要经过三个步骤。分别为训练，预测和分词。下面详细讲解其中所用到的算法。

3.2.2.1 训练

在训练阶段，我们的数据输入为语料库中的中文句子Y，和一系列已经定义好的特征函数$f_i$，输出为特征函数对应的最优权重值$w_i$。加入权重的条件概率$P_w$可以表示为：$$P_w(y|x)=\frac{1}{Z_w(x)}exp(\sum _{k=1}^K{w}_k{f}_k(x,y))=\frac{exp({\sum }_{k=1}^K{w}_k{f}_k(x,y)}{{\sum }_{y}exp({\sum }_{k=1}^K{w}_k{f}_k(x,y)}$$我们的目标则是寻找最优的$w$是的$P_w(y|x)$最大，求解的算法有许多，如梯度下降法，牛顿法，拟牛顿法。
简单的说一下梯度下降法求解CRF参数的算法过程：
（1）写出极大化条件分布$P_w(y|x)$的对数似然函数$L(P_w)$；
（2）令$f(w)=-L(P_w)$，并对$f$进行极小化；
（3）对$f$的极小化公式对$w$进行求导操作，得到求导后的表达式；
（4）利用表达式，用梯度下降法来迭代求解最优的$w$。注意在迭代过程中，每次更新$w$后，需要同步更新$P_w(x,y)$,以用于下一次迭代的梯度计算。

详细算法的推导过程请移步：
条件随机场CRF(三) 模型学习与维特比算法解码；
梯度下降（Gradient Descent）小结

3.2.2.2 预测

在预测阶段，我们的数据输入为观测序列X和CRF模型参数，输出为$argmaxP(y|x)$，也就是$X$条件下取$P(y|x)$的最大值时的隐藏状态序列$I$。这步和HMM的求解过程一样，也是用到了Veterbi算法，只不过将在计算局部最优解时，HMM计算的是：$${\delta }_t(i)=b_i(o_t)ma{x}_{1\le j\le N}[{\delta }_{t-1}(j)a_{ji}]，i=1,2...N$$而CRF则计算的是：$${\delta }_i(l)=ma{x}_{1\le j\le m}\{{\delta }_{i-1}+\sum _{k=1}^K{w}_k{f}_k(y_{i-1}=j,y_i=l,x,i-1)\}，l=1,2...m$$同样的，其记录函数为：$${\psi }_i(l)=argmax({\delta }_i(l))$$通过初始状态，一步一步递推到 $l=m$，然后取最大值的$\psi$，再回溯到初始状态。最终得到观测序列$Y$。

3.2.2.3 分词

与HMM一样，详细请见3.1.2.3章节

3.2.3 CRF代码实践

暂无

---

四、分词知识树结构

---

总结

主要介绍NLP领域常见的分词算法及其对应的推导过程。详细介绍了HMM和CRF统计模型的原理及其相关推导和计算。

---

参考文献：

系列文章目录

第一章 Python NLP实战-核心技术与算法----NLP基础
第二章 Python NLP实战-核心技术与算法----中文分词技术

---