机器学习-白板推导系列笔记（九）-概率图模型

此文章主要是结合哔站shuhuai008大佬的白板推导视频：概率图模型_297min

全部笔记的汇总贴：机器学习-白板推导系列笔记

PS：本次课程所提及的内容，在后面的章节都有讲解，可以先跳过，然后在看完粒子滤波这一章的时候进行回顾复习，我到时候也会在那一章的最后放一个传送门过来的。

一、概述

（一）概率图模型的知识体系

$$概率图\{\begin{array}{c}Representation(表示)\{\begin{array}{c}有向图BeyesianNetwork\\ 高斯图（连续）\{\begin{array}{c}GaussianBN\\ GaussianMN\end{array}\\ 无向图MarkovNetwork\end{array}\\ Inference(推断)\{\begin{array}{c}精确推断\\ 近似推断\{\begin{array}{c}确定性近似（变分推断）\\ 随机近似（MCMC）\end{array}\end{array}\\ Learning(学习)\{\begin{array}{c}参数学习\{\begin{array}{c}完备数据\{\begin{array}{c}有向\\ 无向\end{array}\\ 隐变量\to EM\end{array}\\ 结构学习\end{array}\end{array}$$

（二）基本规则

概率图模型使用图的形式来表示概率分布，下面是几个随机变量分布的一些规则：

$$\begin{gathered} SumRule:p(x_1)=\int p(x_1,x_2)\mathrm{d}{x}_2 \\ ProductRule:p(x_1,x_2)=p(x_1|x_2)p(x_2) \\ ChainRule:p(x_1,x_2,\cdots ,x_p)=\prod _{i=1}^{p}p(x_i|x_{i+1},x_{i+2},\cdots ,x_p) \\ BayesianRule:P(x_2|x_1)=\frac{P(x_1,x_2)}{P(x_1)}=\frac{P(x_1,x_2)}{\int P(x_1,x_2)\mathrm{d}{x}_2}=\frac{P(x_2)P(x_1|x_2)}{\int P(x_2)P(x_1|x_2)\mathrm{d}{x}_2} \end{gathered}$$

（三）简化运算假设

在链式规则中如果数据的维度过高，就会出现计算复杂的困境，因此我们需要对此做出一些简化：

$①$相互独立的假设：$P(x_1,x_2,\cdots ,x_p)={\prod }_{i=1}^{p}P(x_i)$，
朴素贝叶斯中的条件独立性假设：$P(x|y)={\prod }_{i=1}^{p}P(x_i|y)$；
$②$ $MarkovProperty:x_j\perp x_{i+1}|x_i,j<i$，HMM中的齐次Markov假设；
$③$条件独立性假设：$x_A\perp x_B|x_C,x_A、x_B、x_C$是集合，且不相交。

二、有向图-贝叶斯网络

（一）基本结构

已知联合概率分布中各个随机变量的依赖关系，可以根据拓扑排序（依赖关系）得到一个有向图。而如果已知一个有向图，可以直接得到联合概率分布的因子分解：

$$P(x_1,x_2,\cdots ,x_p)=\prod _{i=1}^{p}P(x_i|x_{parent(i)})$$

在局部的任何三个节点，可以有以下三种结构：

• head to tail
  

这种结构满足：

$$A\perp C|B\iff 若B被观测，则路径被阻塞$$

通过因子分解和链式规则可以进行证明：

$$\begin{gathered} P(A,B,C)=\underset{因子分解}{P(A)P(B|A)P(C|B)}=\underset{链式法则}{P(A)P(B|A)P(C|B,A)} \\ \Rightarrow P(C|B)=P(C|B,A) \\ \Rightarrow P(C|B)P(A|B)=P(C|A,B)P(A|B) \\ \Rightarrow P(C|B)P(A|B)=P(C,A|B) \\ \Rightarrow C\perp A|B \end{gathered}$$

• tail to tail
  
  这种结构满足：

$$A\perp C|B\iff 若B被观测，则路径被阻塞$$

通过因子分解和链式规则可以进行证明：

$$\begin{gathered} P(A,B,C)=\underset{因子分解}{P(A|B)P(B)P(C|B)}=\underset{链式法则}{P(B)P(A|B)P(C|A,B)} \\ \Rightarrow P(C|B)=P(C|A,B) \\ \Rightarrow P(C|B)P(A|B)=P(C|A,B)P(C|B) \\ \Rightarrow P(C|B)P(A|B)=P(A,C|B) \\ \Rightarrow C\perp A|B \end{gathered}$$

• head to head
  

这种结构满足：

默认情况下，$A\perp C$，路径是阻塞的。
若$B$被观测，则路径是通的。
如果$B$仍然有后继节点，则如果后继节点被观测，路径也是通的。

通过因子分解和链式规则可以进行证明：

$$\begin{gathered} P(A,B,C)=\underset{因子分解}{P(A)P(C)P(B|A,C)}=\underset{链式法则}{P(A)P(C|A)P(B|A,C)} \\ \Rightarrow P(C)=P(C|A) \\ \Rightarrow A\perp C \end{gathered}$$

（二）其他图

（可以直接看（三），这一小节以（一）为基础，作一些相关图概念的补充知识）
对于团，

团，最大团：图中节点的集合，集合中的节点之间全部互相连接的叫做团，如果不能再添加任何节点，就叫做最大团。

最大团的概念可以参考数据结构中的极大连通子图。

1、道德图

我们常常想将有向图转为⽆向图，从⽽应⽤更⼀般的表达式。对于有向图中的三种结构，有不同的转换方法：

• head to tail

显然可以看出A，B和B，C是团，因此可以直接去掉箭头：

• tail to tail

可以看出A，B和B，C是团，因此可以直接去掉箭头：

• head to head
  说明A，B，C是一个团，需要在A，C之间加一条线：

我们可以得出结论，这三种基本的有向图结构转化为无向图，分为以下两步：

• ①将每个节点的⽗节点两两相连
• ②将有向边替换为⽆向边

得到的无向图就是道德图

2、因子图

对于⼀个有向图，可以通过引⼊环的⽅式，可以将其转换为⽆向图（Tree-like graph），这个图就叫做道德图。但是我们上⾯的 BP 算法只对⽆环图有效，通过因⼦图可以变为⽆环图。

联合概率的因子图分解方法为：

$$P(x)=\prod _S{f}_S(x_S)$$

其中：

• ①$S$：图的节点子集
• ②$x_S:S$的随机变量子集

有以下无向图：

可以将其转换成一个简单的因子图：

其中$f=f(a,b,c)$，对比无向图的因子分解$P(x)=\frac{1}{Z}\psi (a,b,c)$，我们可以看到因子分解本身对应一个特殊的因子图。
因子图不是唯一的，可以看做对因子分解的进一步分解，比如以下分解：

对应的计算公式为$P(x)=f_1(a,b)f_2(a,c)f_3(b,c)f_a(a)f_b(b)f_c(c)$，因式分解不是唯一的，只需要保证乘积等于概率$P(x)$即可。在上面的因式分解中我们可以看做这个因子图分为两层：

也就是说因子图可以做到随机变量节点之间不直接相连，只与因子节点相连，因子节点只与变量节点相连。

（三）$D$划分（D-Seperation）

对于3个集合$A、B、C$，判断其是否满足条件独立性假设（$x_A\perp x_B|x_C,x_A、x_B、x_C$是集合，且不相交。）可以通过$D$划分这种方法。

$D$划分是一种判定的方式，其规则是对于上述head to tail以及tail to tail的关系，引入集合$A、B$，那么满足$x_A\perp x_B|x_C$的$C$集合中的元素与$A、B$中的元素的关系满足head to tail或tail to tail的关系，而满足head to head关系的元素不在C中。

（四）马尔可夫毯（Markov Blanket）

形象一点说，把一个随机变量全集$U$分成互斥的三部分，变量$A$以及集合$C$和$B$，三个子集没有交集，并集即为全集$U$；如果说给定集合$C$时，变量$A$与集合$B$没有任何关系，则称集合$C$为变量$A$的马尔可夫毯。

（五）具体模型

实际应⽤的模型中，对这些条件独⽴性作出了假设，从单⼀到混合，从有限到⽆限（时间，空间）可以分为：

$$\{\begin{array}{c}单一：NaiveBayes\\ 混合：GMM\\ 时间：\{\begin{array}{c}MarkovChain\\ GaussianProcess\end{array}\\ 连续：GaussianBayesianNetwork\end{array}$$

GMM 与时序（$t$）结合的动态模型：

• HMM（离散）
• 线性动态系统 LDS（Kalman 滤波）
• 非线性动态系统 粒⼦滤波（⾮⾼斯，⾮线性）

三、无向图-马尔可夫网络（马尔可夫随机场）

（一）马尔可夫性

马尔可夫随机场的条件独立性体现在三个方面：

• ①全局马尔可夫性
• ②局部马尔可夫性
• ③成对马尔可夫性

全局、局部、成对马尔可夫性是相互等价的，也就是说可以相互推出来。

1、全局马尔可夫性

在无向图中给定三个集合$A、B、C$，在无向图中如果满足给定$x_C$的条件下，$x_A$和$x_B$相互独立，即$x_A\perp x_B|x_C$，则满足全局马尔可夫性。

从图中的判定方法为从$A$中节点到$B$中节点的任何路径上都至少有一个位于$C$中的节点。

2、局部马尔可夫性

局部马尔可夫性是指给定一个变量$x$的所有邻接变量，则$x$独立于任何其他变量，即：

$$x\perp (X-Neighbor(x)-x)|Neighbor(x)$$

对于上图，$a\perp \left\{e,f\right\}|\left\{b,c,d\right\}$：

3、成对马尔可夫性

成对马尔可夫性是指给定所有其他变量，两个非邻接变量条件独立，即：

$$x_i\perp x_j|x_{-i-j}，i\ne j，x_i、x_j不相邻$$

（二）因子分解

将概率无向图模型的联合概率分布表示为其最大团上的随机变量的函数的乘积形式的操作，称为概率无向图模型的因子分解。

给定概率无向图模型，$C_i,i=1,2,\cdots$ ,$k$为无向图模型上的最大团，则$x$的联合概率分布$P(x)$可以写为：

$$P(x)=\frac{1}{Z}\prod _{i=1}^k\psi (x_{C_i})$$
$C_i$：最大团
$x_{C_i}$：最大团随机变量集合
$\psi (x_{C_i})$：势函数，必须为正
$$Z=\sum _x\prod _{i=1}^k\psi (x_{C_i})=\sum _{x_1}\sum _{x_2}\cdots \sum _{x_p}\prod _{i=1}^k\psi (x_{C_i})$$

对于势函数，通常使用$\psi (x_{C_i})=exp\left\{-E(x_{C_i})\right\}$，当使用这个势函数时，$P(x)=\frac{1}{Z}{\prod }_{i=1}^k\psi (x_{C_i})$就叫做吉布斯分布（Gibbs Distribution），或者玻尔兹曼分布（Boltzmann Distribution）。进一步观察一下这个分布：

$$\begin{gathered} P(x)=\frac{1}{Z}\prod _{i=1}^k\psi (x_{C_i}) \\ =\frac{1}{Z}\prod _{i=1}^{k}exp\left\{-E(x_{C_i})\right\} \\ =\underset{指数族分布形式}{\frac{1}{Z}exp\left\{-\sum _{i=1}^{k}E(x_{C_i})\right\}} \end{gathered}$$

也就是说吉布斯分布满足指数族分布的形式，于是满足最大熵原理。

四、概率图模型的推断

总的来说，推断的任务就是求概率。假如我们知道联合概率$P(x)=P(x_1,x_2,\cdots ,x_p)$，我们需要使用推断的方法来求：

边缘概率：$P(x_i)={\sum }_{x_1}\cdots {\sum }_{x_{i-1}}{\sum }_{x_{i+1}}\cdots {\sum }_{x_p}P(x)$
条件概率：$P(x_A|x_B),x=x_A\cup x_B$
$MAPInference：\hat{z}=\underset{z}{\mathrm{argmax}}P(z|x)\propto \underset{z}{\mathrm{argmax}}P(z,x)$

推断方法：

• ①精确推断：

Variable Elimination(VE,变量消除法)(针对树结构)；
Belief Propagation(BP,信念传播,Sum-Product Algo)(针对树结构)；
Junction Tree Algorithm(针对图结构)

• ②近似推断：

Loop Belief Propagation(针对有环图)；
Mente Carlo Inference(例如Importance Sampling,MCMC)；
Variational Inference

五、Variable Elimination（变量消除法）

（一）变量消除法

对于上述图结构，假如我们希望求边缘概率$P(d)$，我们就可以应用变量消除法：

$$\begin{gathered} P(d)=\sum _{a,b,c}P(a,b,c,d) \\ =\underset{因子分解}{\sum _{a,b,c}P(a)P(b|a)P(c|b)P(d|c)} \\ =\sum _{b,c}P(c|b)P(d|c)\underset{{\varphi }_a(b)}{\sum _{a}P(a)P(b|a)} \\ =\sum _{c}P(d|c)\underset{{\varphi }_b(c)}{\sum _{b}P(c|b){\varphi }_a(b)} \\ =\sum _{c}P(d|c){\varphi }_b(c) \\ ={\varphi }_c(d) \end{gathered}$$

（二）枚举法解释

我们可以通过观察直接将$P(d)$展开计算的形式来理解变量消除法的作用。首先我们假设$a，b，c，d$都是离散的二值随机变量，只能取$0$和$1$两个值，然后直接将$P(d)$展开：

$$\begin{gathered} P(d)=\sum _{a,b,c}P(a,b,c,d) \\ =\sum _{a,b,c}P(a)P(b|a)P(c|b)P(d|c) \\ =P(a=0)P(b=0|a=0)P(c=0|b=0)P(d|c=0) \\ +P(a=0)P(b=0|a=0)P(c=1|b=0)P(d|c=1) \\ +P(a=0)P(b=1|a=0)P(c=0|b=1)P(d|c=0) \\ +P(a=0)P(b=1|a=0)P(c=1|b=1)P(d|c=1) \\ +P(a=1)P(b=0|a=1)P(c=0|b=0)P(d|c=0) \\ +P(a=1)P(b=0|a=1)P(c=1|b=0)P(d|c=1) \\ +P(a=1)P(b=1|a=1)P(c=0|b=1)P(d|c=0) \\ +P(a=1)P(b=1|a=1)P(c=1|b=1)P(d|c=1) \\ =8\cdot 因子积 \end{gathered}$$

如果直接计算上式中的每一项再加起来就会需要相当大的计算量，而且上式只是每个变量都是二值变量的情况下，如果每个变量能取更多的值就会有更大的计算量。变量消除法就是根据某些节点只与图中自己的邻接节点有关这一特性来简化计算，相当于应用了乘法分配律（$ab+ac=a(b+c)$）来避免计算每一项在加起来。变量消除法在上式中的计算过程为：

$$\begin{gathered} P(d)=(将与a有关的放到一起) \\ =P(c=0|b=0)P(d|c=0)\cdot P(a=0)P(b=0|a=0) \\ +P(c=1|b=0)P(d|c=1)\cdot P(a=0)P(b=0|a=0) \\ +P(c=0|b=1)P(d|c=0)\cdot P(a=0)P(b=1|a=0) \\ +P(c=1|b=1)P(d|c=1)\cdot P(a=0)P(b=1|a=0) \\ +P(c=0|b=0)P(d|c=0)\cdot P(a=1)P(b=0|a=1) \\ +P(c=1|b=0)P(d|c=1)\cdot P(a=1)P(b=0|a=1) \\ +P(c=0|b=1)P(d|c=0)\cdot P(a=1)P(b=1|a=1) \\ +P(c=1|b=1)P(d|c=1)\cdot P(a=1)P(b=1|a=1) \\ (应用乘法分配律) \\ =P(c=0|b=0)P(d|c=0)\cdot {\varphi }_a(b=0) \\ +P(c=1|b=0)P(d|c=1)\cdot {\varphi }_a(b=0) \\ +P(c=0|b=1)P(d|c=0)\cdot {\varphi }_a(b=1) \\ +P(c=1|b=1)P(d|c=1)\cdot {\varphi }_a(b=1) \\ (将与b有关的放到一起) \\ =P(d|c=0)\cdot P(c=0|b=0){\varphi }_a(b=0) \\ +P(d|c=1)\cdot P(c=1|b=0){\varphi }_a(b=0) \\ +P(d|c=0)\cdot P(c=0|b=1){\varphi }_a(b=1) \\ +P(d|c=1)\cdot P(c=1|b=1){\varphi }_a(b=1) \\ (应用乘法分配律) \\ =P(d|c=0)\cdot {\varphi }_b(c=0) \\ +P(d|c=1)\cdot {\varphi }_b(c=1) \\ ={\varphi }_c(d) \end{gathered}$$

（二）变量消除法的缺点

变量消除的缺点很明显：
①计算步骤⽆法存储：每次计算一个边缘概率就要重新计算一遍整个图；
②消除的最优次序是⼀个$NP-hard$问题：对于复杂的图来说，想要找到一个最优的消除次序是困难的。

六、Belief Propagation（信念传播算法）

（一）Variable Elimination算法的计算重复问题

对于上述马尔可夫链结构，我们已知联合概率：

$$P(a,b,c,d,e)=P(a)P(b|a)P(c|b)P(d|c)P(e|d)$$

我们在计算$e$的边缘概率时，使用变量消除法的步骤如下：

$$\begin{gathered} P(e)=\sum _{a,b,c,d}P(a,b,c,d,e) \\ =\sum _{a,b,c,d}P(a)P(b|a)P(c|b)P(d|c)P(e|d) \\ =\underset{m_{d\to e}(e)}{\sum _{d}P(e|d)\underset{m_{c\to d}(d)}{\sum _{c}P(d|c)\underset{m_{b\to c}(c)}{\sum _{b}P(c|b)\underset{m_{a\to b}(b)}{\sum _{a}P(b|a)P(a)}}}} \end{gathered}$$

我们在计算$c$的边缘概率时，使用变量消除法的步骤如下：

$$\begin{gathered} P(c)=\sum _{a,b,d,e}P(a,b,c,d,e) \\ =\sum _{a,b,d,e}P(a)P(b|a)P(c|b)P(d|c)P(e|d) \\ =(\sum _{b}P(c|b)\sum _{a}P(b|a)P(a))\cdot (\sum _{c}P(d|c)\sum _{d}P(e|d)) \end{gathered}$$

我们发现在计算$c$的边缘概率时的前一部分与在计算$e$的边缘概率时的一部分重复了，可以想象在求其他边缘概率的分布时也会有大量的重复，而Belief Propagation算法就是来解决这个问题。

（二）Belief Propagation的引出

上面我们一直计算的是有向图的马尔可夫链，现在我们将问题从链结构引申到树结构，从有向图引申到无向图（Belief Propagation只针对树状结构）。举例来说，有如下无向树：

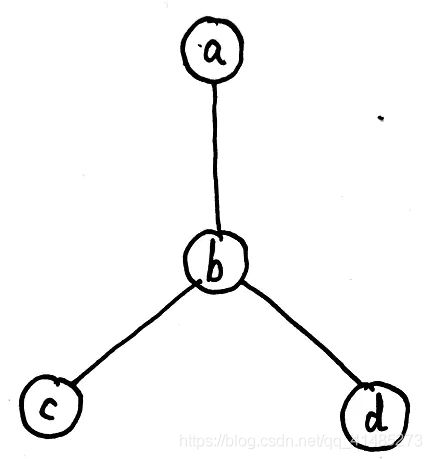
现在我们知道该联合概率的因子分解可以写为：

$$P(a,b,c,d)=\frac{1}{Z}{\psi }_a(a){\psi }_b(b){\psi }_c(c){\psi }_d(d)\cdot {\psi }_{ab}(a,b){\psi }_{bc}(b,c){\psi }_{bd}(b,d)$$

我们要求解边缘概率$P(a)$，也要应用到变量消除法，大体步骤是先消去$c$和$d$，然后再消去$b$，该过程如下所示：

$$p(a)={\psi }_a\underset{m_{b\to a}(a)}{\sum _b{\psi }_b\cdot {\psi }_{ab}(\underset{m_{c\to b}(b)}{\sum _c{\psi }_c\cdot {\psi }_{bc}})(\underset{m_{d\to b}(b)}{\sum _d{\psi }_d\cdot {\psi }_{bd}})}$$

我们可以看到求解的过程主要就是求以下两项（这里写得规范一些，比如$a$写作$x_a$）：

$$\{\begin{array}{c}{m}_{b\to a}(x_a)={\sum }_{x_b}{\psi }_{ab}\cdot {\psi }_b\cdot m_{c\to b}(x_b)\cdot m_{d\to b}(x_b)\\ p(x_a)={\psi }_a\cdot m_{b\to a}(x_a)\end{array}$$

现在我们可以将求解$x_a$边缘概率的过程抽象出来得到求解$x_i$边缘概率的过程：

$$\{\begin{array}{c}{m}_{j\to i}(x_i)={\sum }_{x_j}{\psi }_{ij}\cdot {\psi }_j\cdot {\prod }_{k\in Neighbor(j)-i}{m}_{k\to j}(x_j)\\ p(x_i)={\psi }_i\cdot {\prod }_{k\in Neighbor(j)}{m}_{k\to i}(x_i)\end{array}$$

我们可以继续观察求解$x_i$边缘概率的公式，并对一些部分做一下定义：

$$\{\begin{array}{c}{m}_{j\to i}(x_i)={\sum }_{x_j}{\psi }_{ij}\cdot \underset{belief(x_j)}{\underset{self}{{\psi }_j}\cdot \underset{children}{\prod _{k\in Neighbor(j)-i}{m}_{k\to j}(x_j)}}\\ p(x_i)={\psi }_i\cdot {\prod }_{k\in Neighbor(j)}{m}_{k\to i}(x_i)\end{array}$$

因此求解$m_{j\to i}(x_i)$需要两步：

$$\{\begin{array}{c}belief(x_j)=self\cdot children\\ m_{j\to i}(x_i)={\sum }_{x_j}{\psi }_{ij}\cdot belief(x_j)\end{array}$$

可以想象，在求其他边缘概率时势必会有很多重复的消去过程，但是由于我们已经有了计算$m_{j\to i}(x_i)$的通项，我们就可以利用这个公式来消除计算上的重复，而Belief Propagation算法正是利用了这个通项解决了这个问题。

（三）Belief Propagation

Belief Propagation算法的思想是：

不要直接求$P(a)、P(b)、P(c)、P(d)$，只需求所有的$m_{j\to i}$。

Belief Propagation算法首先求所有的信息传递（收集或分发）的过程得到所有的$m_{j\to i}$（图的遍历），然后套用公式计算边缘概率，总的来说也就是$BP=VE+Caching$。
Belief Propagation算法遍历图的一种方法（Sequential Implementation）如下：

• ①Get root，assume a is root；
• ②Collect Message：

for $x_i$ in Neighbor(Root):
  collectMsg($x_i$)

• ③Distribute Message：

for $x_i$ in Neighbor(Root):
  distributeMsg($x_i$)

还有另外一种遍历的方法（Parellel Implementation），这是一种应用在分布式计算中的方法，可以并行计算。

（四）Max-product

事实上，信念传播算法分为Max-product和 Sum-product，上面讲的属于Sum-product，与Sum-product不同的是Max-product只需要将把求和符号换成求最大值$max$的符号即可。

Max-product是 Sum-Product算法的改进，也是在HMM中应用到的 Viterbi算法的推⼴。

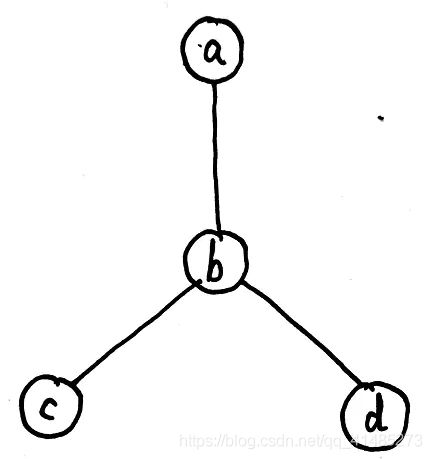
仍然拿上面这种图结构来举例，只画出了要求解的节点（$a，b，c，d$），其他节点（$E$）未画出。
Max-product的作用是用来求一个序列来使得后验概率最大，也就是：

$$(x_a^{\ast },x_b^{\ast },x_c^{\ast },x_d^{\ast })=\underset{x_a,x_b,x_c,x_d}{\mathrm{argmax}}P(x_a,x_b,x_c,x_d|E)$$

求解过程如下：

$$\begin{gathered} ①m_{c\to b}=\underset{x_c}{\max }{\psi }_c\cdot {\psi }_{bc} \\ ②m_{d\to b}=\underset{x_d}{\max }{\psi }_d\cdot {\psi }_{bd} \\ ③m_{b\to a}=\underset{x_b}{\max }{\psi }_b\cdot {\psi }_{ab}\cdot m_{c\to b}\cdot m_{d\to b} \\ ④maxP(x_a,x_b,x_c,x_d)=\underset{x_a}{\max }{\psi }_a\cdot m_{b\to a} \end{gathered}$$

与Sum-product不同的是，在求解$maxP(x_a,x_b,x_c,x_d)$这个过程中我们不需要求$m_{a\to b}、m_{b\to c}、m_{b\to d}$，因为我们需要的是$maxP(x_a,x_b,x_c,x_d)$概率的值和$x_a^{\ast }，x_b^{\ast }，x_c^{\ast }，x_d^{\ast }$这个序列。

下一章传送门：白板推导系列笔记（十）-期望最大算法

参考文章
概率图模型-表示|机器学习推导