Quasi-Newton拟牛顿法（共轭方向法）

1. Introduction

拟牛顿法可以理解为使用迭代的方法近似Hessian矩阵，但是拟牛顿法本质上其实是共轭方向法，所以用共轭方向法来理解拟牛顿法更加贴切。

本文的主要内容来自于《最优化导论》（《An introduction to optimization》）

2. 牛顿法

牛顿法在很多地方都有详细的说明，就不在这里赘述了。

2.1 不能保证收敛

一般的非线性函数，牛顿法不能保证从任意起始点都可以收敛到极小值点。结果可能会随着迭代在极小值附件震荡，甚至越走越远。这就要求我们设置合理的步长。

2.2 Hessian计算复杂

另外牛顿法中Hessian矩阵计算十分复杂，于是就引入了拟牛顿法，可以设计近似矩阵来代替复杂的Hessian矩阵。

3. 共轭方向法

共轭方向法的求解的主要是n维的二次型函数：

通过找到关于Q的一系列共轭方向d，然后分别从每个共轭方向上优化，最终可以在n步之内得到结果。

同时为了更方便的找到共轭方向，引入使用迭代求出共轭方向的方法，如下的共轭梯度法：

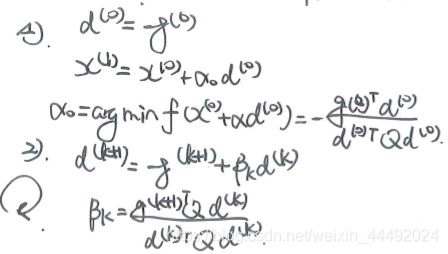
为了说明清楚，我们需要：

• 定义共轭方向
• 通过朝共轭方向更新x，可以收敛到极小值
• 共轭梯度法构造得到的是共轭方向

3.1 共轭方向

共轭方向的定义如下，Q是上面所述的二次型函数中的表达。

关于共轭方向还有一个重要引理：

3.2 共轭方向上可以收敛到极小

3.3 共轭梯度法得到的是Q上的共轭方向

这个可以通过数学归纳法证明，证明可以参见原书。我们只需要知道共轭梯度法得到的d确实是Q的共轭方向。

3.4 算法效果

• 共轭方向法的效率在最速下降法和牛顿法之间。
• 对n维的二次型问题，n步之内可以得到结果。
• 不需要计算Hessian矩阵。
• 也不需要存储n*n的矩阵，不需要求逆运算。

Matlab compare example

%block preconditioning solution
clear all;
ex_blockprecond;

A_full = full(A);
fprintf('\nStarting dense direct solve ...\n');
time_start = cputime;
x_star_dense = A_full\b;
time_end = cputime;
relres_dense = norm(A*x_star_dense - b)/norm(b);
fprintf('Relative residual: %e\n', relres_dense);
fprintf('Dense direct solve done.\nTime taken: %e\n',...
time_end - time_start);

fprintf('\nStarting sparse direct solve ...\n');
time_start = cputime;
x_star_sparse = A\b;
time_end = cputime;
relres_sparse = norm(A*x_star_dense - b)/norm(b);
fprintf('Relative residual: %e\n', relres_sparse)
fprintf('Sparse direct solve done.\nTime taken: %e\n\n',...
time_end - time_start);

fprintf('\nStarting CG ...\n');
time_start = cputime;
[x,flag,relres,iter,resvec] = pcg(A,b,1e-4,200);
time_end = cputime;
fprintf('CG done. Status: %d\nTime taken: %e\n', flag,...
time_end - time_start);
figure; semilogy(resvec/norm(b), '.--'); hold on;
set(gca,'FontSize', 16, 'FontName', 'Times');
xlabel('cgiter'); ylabel('relres');

time_start = cputime;
L = chol(A_blk)';
time_end = cputime;
tchol = time_end - time_start;
fprintf('\nCholesky factorization of A blk. Time taken: %e\n', tchol);

fprintf('\nStarting CG with block preconditioning ...\n');
time_start = cputime;
[x,flag,relres,iter,resvec] = pcg(A,b,1e-8,200,L,L');
time_end = cputime;
fprintf('PCG done. Status: %d\nTime taken: %e\n', flag,...
time_end - time_start);

semilogy(resvec/norm(b), 'k.-'); hold on;
print('-depsc', 'ex_blockprecond_relres.eps');
fprintf('Total time block preconditioned PCG: %e\n',...
tchol+time_end - time_start);

4. 拟牛顿法

逆牛顿法的主要步骤如下，它实质上是一致共轭方向法。可以发现，它其实是构造了一系列共轭方向，然后用共轭方向法更新变量x。

4.1 拟牛顿法构造的是Q的共轭方向

• 拟牛顿法是共轭方向法，可以在n此迭代内得到结果。
• 拟牛顿法是通过H迭代构造共轭方向，H的构造则有很多方法，下面介绍几个常用的。

4.2 确定Hk - 秩1修正公式

4.2 确定Hk - DFP

4.3 确定Hk - BFGS

由于我们在运算中使用的都是H的逆，于是BFGS只关注H的逆（记为B）。

4.4 BFGS ceres

BFGS ceres 代码可以在这里找到ceres中实现BFGS的代码步骤。
为了理解代码，我们先写出BFGS的另一种表达方式，并且证明它与上面的表达式是等价的。

      // Efficient O(num_parameters^2) BFGS update [2].
      //
      // Starting from dense BFGS update detailed in Nocedal [2] p140/177 and
      // using: y_k = delta_gradient, s_k = delta_x:
      //
      //   \rho_k = 1.0 / (s_k' * y_k)
      //   V_k = I - \rho_k * y_k * s_k'
      //   H_k = (V_k' * H_{k-1} * V_k) + (\rho_k * s_k * s_k')
      //
      // This update involves matrix, matrix products which naively O(N^3),
      // however we can exploit our knowledge that H_k is positive definite
      // and thus by defn. symmetric to reduce the cost of the update:
      //
      // Expanding the update above yields:
      //
      //   H_k = H_{k-1} +
      //         \rho_k * ( (1.0 + \rho_k * y_k' * H_k * y_k) * s_k * s_k' -
      //                    (s_k * y_k' * H_k + H_k * y_k * s_k') )
      //
      // Using: A = (s_k * y_k' * H_k), and the knowledge that H_k = H_k', the
      // last term simplifies to (A + A'). Note that although A is not symmetric
      // (A + A') is symmetric. For ease of construction we also define
      // B = (1 + \rho_k * y_k' * H_k * y_k) * s_k * s_k', which is by defn
      // symmetric due to construction from: s_k * s_k'.
      //
      // Now we can write the BFGS update as:
      //
      //   H_k = H_{k-1} + \rho_k * (B - (A + A'))

      // For efficiency, as H_k is by defn. symmetric, we will only maintain the
      // *lower* triangle of H_k (and all intermediary terms).

如上面的ceres的描述中描述的，对BFGS中的参数做了进一步标记：


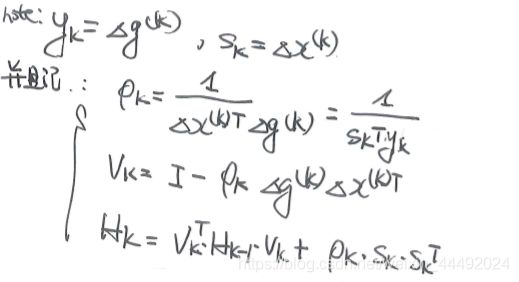
然后可以自然的得到下面的代码：

      const double rho_k = 1.0 / delta_x_dot_delta_gradient;

      // Calculate: A = s_k * y_k' * H_k
      Matrix A = delta_x * (delta_gradient.transpose() *
                            inverse_hessian_.selfadjointView());

      // Calculate scalar: (1 + \rho_k * y_k' * H_k * y_k)
      const double delta_x_times_delta_x_transpose_scale_factor =
          (1.0 + (rho_k * delta_gradient.transpose() *
                  inverse_hessian_.selfadjointView() *
                  delta_gradient));
      // Calculate: B = (1 + \rho_k * y_k' * H_k * y_k) * s_k * s_k'
      Matrix B = Matrix::Zero(num_parameters_, num_parameters_);
      B.selfadjointView().
          rankUpdate(delta_x, delta_x_times_delta_x_transpose_scale_factor);

      // Finally, update inverse Hessian approximation according to:
      // H_k = H_{k-1} + \rho_k * (B - (A + A')).  Note that (A + A') is
      // symmetric, even though A is not.
      inverse_hessian_.triangularView() +=
          rho_k * (B - A - A.transpose());
    }

    *search_direction =
        inverse_hessian_.selfadjointView() *
        (-1.0 * current.gradient);