初识微积分一
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "last_expr"
import numpy as np
from matplotlib import pyplot as plt
变化率
对于函数 y = f ( x ) {y = f(x)} y=f(x) 定义变化率为:
r o c = Δ y Δ x roc = \frac{\Delta{y}}{\Delta{x}} roc=ΔxΔy
代入函数曲线上的两点,可以计算 m {m} m :
r o c = f ( x 2 ) − f ( x 1 ) x 2 − x 1 roc = \frac{f(x_{2}) - f(x_{1})}{x_{2} - x_{1}} roc=x2−x1f(x2)−f(x1)
例如 f ( x ) = x 2 + x {f(x) = x^{2} + x} f(x)=x2+x
def f(x):
return (x)**2 + x
x = np.array(range(0, 11))
y = np.array([0,10])
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.plot(x, f(x), color='g')
plt.plot(y, f(y), color='m')
plt.show()
极限
例:
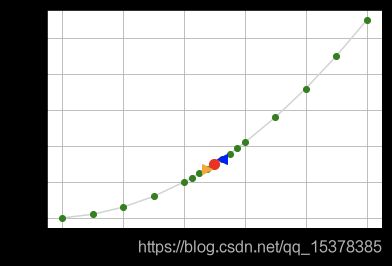
l i m x → 5 f ( x ) lim_{x \to 5} f(x) limx→5f(x)
%matplotlib widget
x = [*range(0,5), *np.arange(4.25, 6, 0.25), *range(6, 11)]
y = [f(i) for i in x]
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid()
plt.plot(x,y, color='lightgrey', marker='o', markeredgecolor='green', markerfacecolor='green')
plt.plot(5, f(5), color='red', marker='o', markersize=10)
plt.plot(5.25, f(5.25), color='blue', marker='<', markersize=10)
plt.plot(4.75, f(4.75), color='orange', marker='>', markersize=10)
plt.show()
FigureCanvasNbAgg()
连续性
对函数 g ( x ) = − ( 12 2 x ) 2 , x ≠ 0 {g(x) = -(\frac{12}{2x})^{2},\;\; x \ne 0} g(x)=−(2x12)2,x=0 画出图形
%matplotlib widget
def g(x):
if x != 0:
return -(12/(2*x))**2
x = range(-20, 21)
y = [g(a) for a in x]
plt.xlabel('x')
plt.ylabel('g(x)')
plt.grid()
plt.plot(x,y, color='g')
xy = (0,g(1))
plt.annotate('O',xy, xytext=(-0.7, -37),fontsize=14,color='b')
plt.show()
FigureCanvasNbAgg()
函数 h ( x ) = 2 x , x ≥ 0 {h(x) = 2\sqrt{x},\;\; x \ge 0} h(x)=2x,x≥0 是不连续的。
%matplotlib inline
def h(x):
if x >= 0:
import numpy as np
return 2 * np.sqrt(x)
x = range(-20, 21)
y = [h(a) for a in x]
plt.xlabel('x')
plt.ylabel('h(x)')
plt.grid()
plt.plot(x,y, color='g')
plt.plot(0, h(0), color='g', marker='o', markerfacecolor='g', markersize=10)
plt.show()
函数 k ( x ) = { x + 20 , if x ≤ 0 , x − 100 , otherwise { k(x) = \begin{cases} x + 20, & \text{if } x \le 0, \\ x - 100, & \text{otherwise }\end{cases}} k(x)={ x+20,x−100,if x≤0,otherwise 是不连续的。
%matplotlib inline
def k(x):
import numpy as np
if x <= 0:
return x + 20
else:
return x - 100
x1 = range(-20, 1)
x2 = range(1, 20)
y1 = [k(i) for i in x1]
y2 = [k(i) for i in x2]
plt.xlabel('x')
plt.ylabel('k(x)')
plt.grid()
plt.plot(x1,y1, color='g')
plt.plot(x2,y2, color='g')
plt.plot(0, k(0), color='g', marker='o', markerfacecolor='g', markersize=10)
plt.plot(0, k(0.0001), color='g', marker='o', markerfacecolor='w', markersize=10)
plt.show()
无穷
对
d ( x ) = 4 x − 25 , x ≠ 25 d(x) = \frac{4}{x - 25},\;\; x \ne 25 d(x)=x−254,x=25
当 x → 25 {x \to 25} x→25 时:
%matplotlib inline
def d(x):
if x != 25:
return 4 / (x - 25)
x = [*range(-100, 24), *np.arange(24.9, 25.2, 0.1), *range(26, 101)]
y = [d(i) for i in x]
plt.xlabel('x')
plt.ylabel('d(x)')
plt.grid()
plt.plot(x,y, color='purple')
plt.show()
l i m x → 2 5 + d ( x ) = ∞ lim_{x \to 25^{+}} d(x) = \infty limx→25+d(x)=∞
l i m x → 2 5 − d ( x ) = − ∞ lim_{x \to 25^{-}} d(x) = -\infty limx→25−d(x)=−∞
对函数 e ( x ) = { 5 , if x = 0 , 1 + x 2 , otherwise {e(x) = \begin{cases} 5, & \text{if } x = 0, \\ 1 + x^{2}, & \text{otherwise } \end{cases}} e(x)={ 5,1+x2,if x=0,otherwise 求 x → 0 { {x\to0}} x→0 时的极限:
lim x → 0 a ( x ) ≠ a ( 0 ) \lim_{x \to 0} a(x) \ne a(0) x→0lima(x)=a(0)
lim x → 0 a ( x ) = 1 \lim_{x \to 0} a(x) = 1 x→0lima(x)=1
%matplotlib inline
def e(x):
if x == 0:
return 5
else:
return 1 + x**2
x= [-1, -0.5, -0.2, -0.1, -0.01, 0.01, 0.1, 0.2, 0.5, 1]
y =[e(i) for i in x]
plt.xlabel('x')
plt.ylabel('e(x)')
plt.grid()
plt.plot(x, y, color='m')
plt.scatter(0, e(0), color='m')
plt.plot(0, 1, color='m', marker='o', markerfacecolor='w', markersize=10)
plt.show()
对函数
g ( x ) = x 2 − 1 x − 1 , x ≠ 1 g(x) = \frac{x^{2} - 1}{x - 1}, x \ne 1 g(x)=x−1x2−1,x=1
求 x → 1 {x \to 1} x→1 时的极限:
l i m x → a g ( x ) = ( x − 1 ) ( x + 1 ) x − 1 lim_{x \to a} g(x) = \frac{(x-1)(x+1)}{x - 1} limx→ag(x)=x−1(x−1)(x+1)
l i m x → a g ( x ) = x + 1 lim_{x \to a} g(x)= x+1 limx→ag(x)=x+1
l i m x → 1 g ( x ) = 2 lim_{x \to 1} g(x) = 2 limx→1g(x)=2
类似的,对函数
h ( x ) = x − 2 x − 4 , x ≠ 4 and x ≥ 0 h(x) = \frac{\sqrt{x} - 2}{x - 4}, x \ne 4 \text{ and } x \ge 0 h(x)=x−4x−2,x=4 and x≥0
求 x → 4 {x \to 4} x→4 时的极限:
l i m x → a h ( x ) = 1 x + 2 lim_{x \to a}h(x) = \frac{1}{ {\sqrt{x} + 2}} limx→ah(x)=x+21
l i m x → 4 h ( x ) = 1 4 + 2 = 1 4 lim_{x \to 4}h(x) = \frac{1}{ {\sqrt{4} + 2}} = \frac{1}{4} limx→4h(x)=4+21=41
极限的算术运算
l i m x → a ( j ( x ) + l ( x ) ) = lim x → a j ( x ) + lim x → a l ( x ) lim_{x \to a} (j(x) + l(x)) = \lim_{x \to a} j(x) + \lim_{x \to a} l(x) limx→a(j(x)+l(x))=x→alimj(x)+x→aliml(x)
l i m x → a ( j ( x ) − l ( x ) ) = lim x → a j ( x ) − lim x → a l ( x ) lim_{x \to a} (j(x) - l(x)) = \lim_{x \to a} j(x) - \lim_{x \to a} l(x) limx→a(j(x)−l(x))=x→alimj(x)−x→aliml(x)
l i m x → a ( j ( x ) ⋅ l ( x ) ) = lim x → a j ( x ) ⋅ lim x → a l ( x ) lim_{x \to a} (j(x) \cdot l(x)) = \lim_{x \to a} j(x) \cdot \lim_{x \to a} l(x) limx→a(j(x)⋅l(x))=x→alimj(x)⋅x→aliml(x)
l i m x → a j ( x ) l ( x ) = lim x → a j ( x ) lim x → a l ( x ) lim_{x \to a} \frac{j(x)}{l(x)} = \frac{\lim_{x \to a} j(x)}{\lim_{x \to a} l(x)} limx→al(x)j(x)=limx→al(x)limx→aj(x)
l i m x → a ( j ( x ) ) n = ( lim x → a j ( x ) ) n lim_{x \to a} (j(x))^{n} = \Big(\lim_{x \to a} j(x)\Big)^{n} limx→a(j(x))n=(x→alimj(x))n