SVM分类与回归
SVM(支撑向量机模型)是二(多)分类问题中经常使用的方法,思想比较简单,但是具体实现与求解细节对工程人员来说比较复杂,如需了解SVM的入门知识和中级进阶可点此下载。本文从应用的角度出发,使用Libsvm函数库解决SVM模型的分类与回归问题。
说明:libsvm是实现svm的便捷开源工具,应用广泛,由国立台湾大学Chih-Chung Chang和Chih-Jen Lin编写,可以实现基于SVM的分类和回归。
1.分类
在Matlab下下载测试数据heart_sacle
运行程序:
load heart_scale; train_data = heart_scale_inst(1:150,:); train_label = heart_scale_label(1:150,:); test_data = heart_scale_inst(151:270,:); test_label = heart_scale_label(151:270,:); train_data=sparse(train_data); test_data=sparse(test_data); libsvmwrite('traindata',train_label,train_data); libsvmwrite('testdata',test_label,test_data);
这样得到的traindata和testdata中的数据结构和heart_scale_c相同。
训练部分:
[xlabel,xdata]=libsvmread('traindata'); xdata=full(xdata); model=svmtrain(xlabel,xdata);%%具体参数可以参见svmtrain.c
返回模型的参数:
结构[Parameters, nr_class, totalSV, rho, Label, ProbA, ProbB, nSV, sv_coef, SVs]
model.Parameters参数意义从上到下依次为:
-s svm类型:SVM设置类型(默认0)
-t 核函数类型:核函数设置类型(默认2)
-d degree:核函数中的degree设置(针对多项式核函数)(默认3)
-g r(gama):核函数中的gamma函数设置(针对多项式/rbf/sigmoid核函数) (默认类别数目的倒数)
-r coef0:核函数中的coef0设置(针对多项式/sigmoid核函数)((默认0)
model.nr_class表示数据集中有多少类别;= 2 for regression/one-class svm
model.Label表示数据集中类别的标签都是什么
model.totalSV代表总共的支持向量的数目
model.nSV表示每类样本的支持向量的数目
model.ProbA和model.ProbB
使用-b参数时才能用到,用于概率估计。
-b probability_estimates: whether to train a SVC or SVR model for probability estimates,0 or 1 (default 0)
可以参见《A note on Platt’s probabilistic outputs for support vector machines》论文
model.sv_coef是一个totalSV*1的矩阵,承装的是totalSV个支持向量在决策函数中的系数
model.SVs是一个totalSV×维度的稀疏矩阵,承装的是totalSV个支持向量
model.rho是决策函数中的常数项的相反数
测试部分:
[clabel,cdata]=libsvmread('testdata'); cdata=full(cdata); [predict_label, accuracy, dec_values] = svmpredict(clabel, cdata, model);
返回参数:
predict_label是预测标签向量
accuracy从上到下依次的意义分别是:
-分类准率(分类问题中用到的参数指标)
-平均平方误差(MSE (mean squared error))[回归问题中用到的参数指标]
-平方相关系数(r2 (squared correlation coefficient))[回归问题中用到的参数指标]
dec_values是一个包含decision值或概率估计(-b 1)的矩阵,如果k个类,对于decision值,每行包含k(k-1)/2个二分类问题的结果;对于概率,每列包含k个属于每类的概率值
改变参数后:
model2=svmtrain(xlabel,xdata,'-c 1024 -g 0.001953125'); [predict_label2, accuracy2, dec_values2] = svmpredict(clabel, cdata, model2); 或 model2=svmtrain(xlabel,xdata,'-c 8 -g 0.03125 -b 1'); [b_label, b_accuracy, prob_estimates] = svmpredict(clabel, cdata, model2, '-b 1');
附加注意事项:
1.缩放训练和测试数据(上例Matlab数据已缩放)
应用SVM之前,缩放是非常重要的。缩放的最主要优点是能够避免大数值区间的属性过分支配了小数值区间的属性。另一个优点能避免计算过程中数值复杂度。因为关键值通常依赖特征向量的内积(inner products),例如,线性核和多项式核力,属性的大数值可能会导致数值问题。我们推荐将每个属性线性缩放到区间[-1,+1]或者[0, 1]。
当然,我们必须使用同样的方法缩放训练数据和测试数据。例如,假设我们把训练数据的第一个属性从[-10, +10]缩放到[-1, +1],那么如果测试数据的第一个属性属于区间[-11, +8],我们必须将测试数据转变成[-1.1, +0.8]。
svm-scale [options] data_filename
范围用-l, -u 指定,通常是[0,1],或是[-1,1]。(文本分类一般选[0,1])。
示例程序:训练集合测试集被分别缩放到[0,1]区间
$ ../svm-scale -l 0 -s range4 svmguide4 > svmguide4.scale $ ../svm-scale -r range4 svmguide4.t > svmguide4.t.scale $ python easy.py svmguide4.scale svmguide4.t.scale rem(libsvm中tools的程序) Accuracy = 89.4231% (279/312) (classification)
2.采用交叉验证选择最佳参数C与g(径向基核函数)
不同的参数(最常用的就是g和c)条件下会训练出不同的SVM,那怎么选取使SVM最好的参数呢,grid.py就是做这个的。
因此,这里要先用grid选取合适的C和g值。
Usage: grid.py [-log2c begin,end,step] [-log2g begin,end,step] [-v fold][-svmtrain pathname] [-gnuplot pathname] [-out pathname] [-png pathname][additional parameters for svm-train] dataset
一般log2c -10,10,1 ;log2g 10,-10,-1, -v 5即可
示例:
python grid.py -log2c -10,10,1 -log2g 10,-10,-1 trainset.scale
返回best-c和best-g,还同时还返回准确率。
3.上述Matlab操作在cmd命令窗口下也可完成,详见《A Practical Guide to Support Vector Classi cation》
2.回归
步骤:使用Libsvm中的Windows版本的工具svmscale.exe进行训练和测试数据的归一化,svmtrain.exe进行模型训练,svmpredict.exe进行预测
1.svmtrtrain.exe训练模型(归一化数据和分类问题类似)
svmtrain.exe -s 3 -p 0.0001 -t 2 -g 32 -c 0.53125 feature.scaled
-s用来指定的SVM的类型(default 0)
0 – C-SVC
1 – nu-SVC
2 – one-class SVM
3 – epsilon-SVR
4 – nu-SVR
对于回归来说,只能选3或者4,3表示epsilon-support vector regression, 4表示nu-support vector regression。-t是选择核函数,通常选用RBF核函数,原因在“A Practical Guide support vector classification”中已经简单介绍过了。-p尽量选个比较小的数字。需要仔细调整的重要参数是-c和-g。除非用gridregression.py来搜索最优参数,否则只能自己慢慢试了。
用gridregression.py搜索最优参数的方法如下:
python.exe gridregression.py -svmtrain H:\SVM\libsvm-2.81\windows\svmtrain.exe -gnuplot C:\gp373w32\pgnuplot.exe -log2c -10,10,1 -log2g -10,10,1 -log2p -10,10,1 -v 10 -s 3 -t 2 H:\SVM\libsvm-2.81\windows\feature.scaled > gridregression_feature.parameter
注意:-svmtrain是给出svmtrain.exe所在路径,一定要是完整的全路径
-gnuplot是给出pgnuplot.exe所在路径。这里要用pgnuplot.exe这种命令行形式的,不要用wgnupl32.exe,这个是图形界面的。
-log2c是给出参数c的范围和步长
-log2g是给出参数g的范围和步长
-log2p是给出参数p的范围和步长
上面三个参数可以用默认范围和步长
-s选择SVM类型,也是只能选3或者4
-t是选择核函数
-v 10 将训练数据分成10份做交叉验证。默认为5
最后给出归一化后训练数据的全路径
搜索最优参数的过程写入文件gridregression_feature.parameter(注意别少了这个>符号啊)
打开gridregression_feature.parameter,下面最后一行分别为c,g,p,mse。其中mse没有用,其实这个值越小越好。
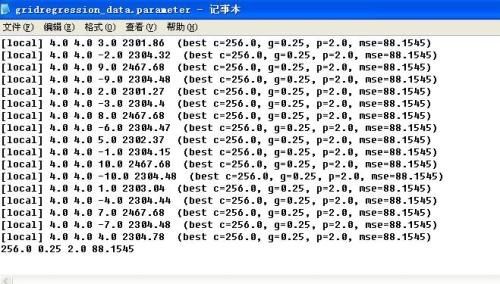
根据搜索到的3个参数进行训练修改feature.scaled.model中的参数。
2.用svmpredict.exe进行预测
svmpredict.exe feature_test.scaled feature.scaled.model feature_test.predicted
其中feature_test.scaled是归一化后的测试特征文件名,feature.scaled.model是训练好的模型,SVM预测的值在feature_test.predicted中。
3.使用libsvm解决回归问题,入门视频详见http://www.tudou.com/programs/view/o0Xn1RzFhOw/