python3 实现狄克斯特拉(Dijkstra)算法 实现加权最短路径规划

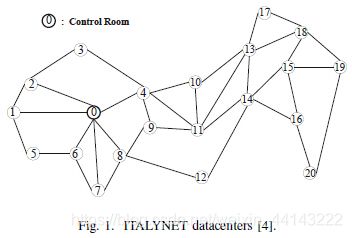
狄克斯特拉算法大致思路是，把每个坐标节点都命一个名(本代码中是1-20)，以及列出每个节点的相邻节点，和到相邻节点的长度(权值)，通过计算得出最短的路径。
实现代码：具体思路详见代码注释

from collections import defaultdict
from heapq import *


def dijkstra_raw(edges, from_node, to_node):
    g = defaultdict(list)
    for l, r, c in edges:
        g[l].append((c, r))
    q, seen = [(0, from_node, ())], set()
    while q:
        (cost, v1, path) = heappop(q)
        if v1 not in seen:
            seen.add(v1)
            path = (v1, path)
            if v1 == to_node:
                return cost, path
            for c, v2 in g.get(v1, ()):
                if v2 not in seen:
                    heappush(q, (cost + c, v2, path))
    return float("inf"), []


def dijkstra(edges, from_node, to_node):
    len_shortest_path = -1
    ret_path = []
    length, path_queue = dijkstra_raw(edges, from_node, to_node)
    if len(path_queue) > 0:
        len_shortest_path = length  ## 1. 先求长度
        ## 2. 分解path_queue，以获得最短路径中的传递节点
        left = path_queue[0]
        ret_path.append(left)  ## 2.1 首先记录目标节点;
        right = path_queue[1]
        while len(right) > 0:
            left = right[0]
            ret_path.append(left)  ## 2.2 记录其他节点，直到源节点。
            right = right[1]
        ret_path.reverse()  ## 3. 最后反转列表，使其成为正常序列。
    return len_shortest_path, ret_path


### ====================给一个所有节点的列表
list_nodes_id = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20];
### ==================== 给一个拓扑的常数矩阵.
M = 99999  # 这代表一段很长的距离。这意味着没有联系。
### M_topo是表示拓扑的二维邻接矩阵
M_topo = [
    [M, 2.9, 2.5, M, 2, M, 1.8, 3, 1.8, M, M, M, M, M, M, M, M, M, M, M, M],  # 0
    [2.9, M, 1.3, M, M, 1.7, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M],  # 1
    [1, 1, M, 1, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M],  # 2
    [M, M, 1, M, 1, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M],  # 3
    [1, M, M, 1, M, M, M, M, M, 1, 1, 1, M, M, M, M, M, M, M, M, M],  # 4
    [M, 1, M, M, M, M, 1, M, M, M, M, M, M, M, M, M, M, M, M, M, M],  # 5
    [1, M, M, M, M, 1, M, 1, M, M, M, M, M, M, M, M, M, M, M, M, M],  # 6
    [1, M, M, M, M, M, 1, M, 1, M, M, M, M, M, M, M, M, M, M, M, M],  # 7
    [1, M, M, M, M, M, M, 1, M, 1, M, M, 1, M, M, M, M, M, M, M, M],  # 8
    [M, M, M, M, 1, M, M, M, 1, M, M, 1, M, M, M, M, M, M, M, M, M],  # 9
    [M, M, M, M, 1, M, M, M, M, M, M, 1, M, 1, M, M, M, M, M, M, M],  # 10
    [M, M, M, M, 1, M, M, M, M, 1, 1, M, M, 1, 1, M, M, M, M, M, M],  # 11
    [M, M, M, M, M, M, M, M, 1, M, M, M, M, M, 1, M, M, M, M, M, M],  # 12
    [M, M, M, M, M, M, M, M, M, M, 1, 1, M, M, 1, M, M, 1, 1, M, M],  # 13
    [M, M, M, M, M, M, M, M, M, M, M, 1, 1, 1, M, 1, 1, M, M, M, M],  # 14
    [M, M, M, M, M, M, M, M, M, M, M, M, M, M, 1, M, 1, M, 1, 1, M],  # 15
    [M, M, M, M, M, M, M, M, M, M, M, M, M, M, 1, 1, M, M, M, M, 1],  # 16
    [M, M, M, M, M, M, M, M, M, M, M, M, M, 1, M, M, M, M, 1, M, M],  # 17
    [M, M, M, M, M, M, M, M, M, M, M, M, M, 1, M, 1, M, 1, M, 1, M],  # 18
    [M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, 1, M, M, 1, M, 1],  # 19
    [M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, 1, M, M, 1, M],  # 20
]

### --- 读取拓扑，并生成给定拓扑中的所有边。
edges = []
for i in range(len(M_topo)):
    for j in range(len(M_topo[0])):
        if i != j and M_topo[i][j] != M:
            edges.append((i, j, M_topo[i][j]))  ### (i,j) 是一个链接;M_topo[i][j]这里是1，链接的长度(i,j).

start = int(input("请输入起始点："))
end = int(input("请输入终点："))
print("=== Dijkstra算法 ===")
print("找从 %s 到 %s的最短路径:" % (start, end))
length, Shortest_path = dijkstra(edges, start, end)
print('长度 = ', length)
print('最短路径是 ', Shortest_path)

运行效果如图所示：