2020年7月B组C++蓝桥杯真题试水
哇!刚刚突然发现我的那篇扩展欧几里得达到了500+的阅读量,开森森~ 看起来努力就是有回报的嘛!用心写的文章和不用心写的文章相信广大程序员萌都一眼看得出来撒~
快乐!你们的关注和点赞是我最大的动力嗷!┗|`O′|┛

好了,闲话不多说~ 正片开始!
A.跑步训练
这个题个人不建议写程序,直接手算就好了,但是要注意的是,每一轮-600然后+300,就相当于-300,但是!一定要记得这-300的时间是120s,而不是60s,手算党千万要小心!检查检查再检查,这个分丢得相当不值得。
结果:3880
B.纪念日

日期题目年年有,一点都不稀奇~关键在于快速A,听说C++算日期很麻烦,谁要咱也不是Java选手呢,害,鱼和熊掌⑧可兼得嘛,祭上大杀器——计算器!
 结果:52038720
结果:52038720
C.合并检测

这个题,数学功底相当强 懒得写程序的我,直接手算!

结果:10
D.REPEAT程序

先说好啊,这玩意不是按照样例算的,实战的时候人家是给了数据的,是一个txt文件,那玩意长的,保证你放弃硬写出这些个循环的想法。
我重新梳理了一遍带佬的思路,然后附上了详细注释
#include 结果:241830
E.矩阵

这题很容易让人想起我们之前做过的那一道DP+打表的题目,有人说DP本质就是打表,我觉得可以这么说,起码以目前我不太高深的实力,可以这么理解。
首先我们自己列出小数据表格,然后根据列出的表格找规律并且写代码。
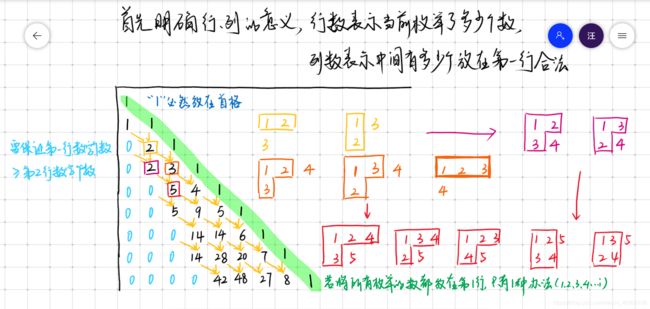
这样的填表莫名让我想起了小学课本上的那个找国王要米的人,在棋盘上堆米直到堆成山。。
其实自己在草稿纸上画一画很容易发现规律——也就是我们要的递推式。
代码就很好写了~~
#include F.整除序列

苦等了这么久终于来了一道签到题!/(ㄒoㄒ)/~~
蓝桥是不是变了呜呜呜
#include G.解码

签到×2!果然不会让咱们太难看哈~
我呵呵呵我又不审题!我把字母l看成了1,哭晕。。我难看了,对八七!我反省!我以后一定好好审题!
// #include H.走方格
#include I.整数拼接

这题,确实没思路,要是暴力肯定炸,于是瞪着带佬没有注释的代码看了一个小时,终于。。懂了,现在给亲爱的读者朋友们奉上注释~
#include 为什么(m-x%m)和x%m是契合的呢?
我们来研究一个案例就清楚了——
45为什么可以整除3?
因为40%3=1(这一部分余三多一),而3-5%3也=1(这一部分余三少一),刚刚好,一拍即合!加起来就可以整除3。这也就是ans += cnt[len][(m-x%m)%m]的理由。
J.网络分析
最后一题拖了三天了QWQ,效率太低了(废物哇的一声哭出来)


这题,不是裸的并查集,注意标黄部分。
每次新的结点加入之后,之前集合中的点加上的值是不能算在新人头上的,洗澡的时候想到了,每次新人加入的时候,就问问自己的父亲现在手上有多少值,然后自己的结点就要减去前人积累(也就是加入的时候父亲的值)的值,最后在输出的时候检查是否是根结点,如果不是就要加上父亲的值,等于新人加入之后的值之和。
本来想的是每个点都标记前人的值,后来借鉴了带佬的思路,每次在merge的时候减去根结点的值,然后再在最后加回来,就是加入之后的值,还是觉得这样比较简单。
#include 


