特征工程阅读笔记(第三章)
特征工程–思维导图
- KNN算法
- K-means算法
KNN算法
算法过程
-
计算待分类观察值与其他观察值之间的距离
x k 是 点 X 的 坐 标 ( x 1 , x 2 , . . . , x n ) x_k 是点X的坐标(x_1,x_2,...,x_n) xk是点X的坐标(x1,x2,...,xn)
y k 是 点 Y 的 坐 标 ( y 1 , y 2 , . . . , y n ) y_k 是点Y的坐标(y_1,y_2,...,y_n) yk是点Y的坐标(y1,y2,...,yn)
欧氏距离:
d ( x , y ) = ∑ k = 1 n ( x k − y k ) 2 d(x,y)=\sqrt{\sum_{k=1}^n(x_k-y_k)^2} d(x,y)=k=1∑n(xk−yk)2
曼哈顿距离:
d ( x , y ) = ∑ k = 1 n ∣ x k − y k ∣ d(x,y)=\sqrt{\sum_{k=1}^n|x_k-y_k|} d(x,y)=k=1∑n∣xk−yk∣ -
将以上求得的距离按照递增关系排序
-
选取距离最小的K个点,列出他们所在的类标签
-
确定每个标签的出现次数
-
选择出现次数最多的类标签为待分类观察值的类标签
代码示例
/**
*计算两点之间的欧氏距离
* @function distance
* @param {[Number, Number]} x
* @param {[Number, Number]} y
* @return {Number} dt
*/
let distance = (x, y) => {
let dt = 0;
for (let i = 0; i < 2; i++) {
dt += (x[i] - y[i]) * (x[i] - y[i]);
}
return {
distance: Math.sqrt(dt), category: y[2] };
};
/**
* 冒泡排序,两两比较,每次都将最大值放在最右边的过程
* @function Bubblesort
* @param {[Dict]} disSet
* @returns {[Dict]}
*/
let Bubblesort = (disSet) => {
let len = disSet.length;
//大循环是来回检查,检查了len-1次
for (let i = 0; i < len - 1; i++) {
//小循环是排序,小循环每次都会把最大的放在最右边[所以小循环只要比较len-i次]
for (let j = 0; j < len - 1 - i; j++) {
if (disSet[j].distance > disSet[j + 1].distance) {
let temp = disSet[j + 1];
disSet[j + 1] = disSet[j];
disSet[j] = temp;
}
}
}
return disSet;
};
/**
* 选择排序,每次都遍历最小的放在最左边
* @function selectionSort
* @param {[Dict]} disSet
* @returns {[Dict]}
*/
let selectionSort = (disSet) => {
let len = disSet.length;
let minIndex, temp;
//大循环: i是从左到右的位置
for (let i = 0; i < len - 1; i++) {
minIndex = i;
//小循环用来确定最小值的索引
for (let j = i + 1; j < len; j++) {
if (disSet[j].distance < disSet[minIndex].distance) {
minIndex = j;
}
}
temp = disSet[i];
disSet[i] = disSet[minIndex];
disSet[minIndex] = temp;
}
return disSet;
};
/**
* 插入排序
* @function insertionSort
* @param {[Dict]} disSet
* @returns {[Dict]}
*/
let insertionSort = (disSet) => {
let len = disSet.length;
let preIndex, current;
//从第二个开始比较
for (let i = 1; i < len; i++) {
preIndex = i - 1;
current = disSet[i];
//比如当前是第五个,current = disSet[4],要比较从3->0的距离
while (preIndex >= 0 && disSet[preIndex].distance > current.distance) {
//只要前边的某个值比第五个大,就将这个值向后移一位
disSet[preIndex + 1] = disSet[preIndex];
//同时指针再往前移动一位
preIndex--;
}
//最终preIndex往前移到了第1位,发现第五位大于第一位,则将第五位安插在第二位的位置
disSet[preIndex + 1] = current;
}
return disSet;
};
/**
* 希尔排序,利用插入排序的优点:有序程度越高,效率越高
* @function shellSort
* @param {[Dict]} disSet
* @returns {[Dict]}
*/
let shellSort = (disSet) => {
let len = disSet.length,
j,
temp,
gap = 1;
/**
* gap(n+1) = 3 * gap(n) + 1
* Z变换可解gap为幂次函数
* 设len = 16,则gap = 13, 4, 1
*/
while (gap < len / 3) {
gap = gap * 3 + 1;
}
while (gap > 0) {
for (let i = gap; i < len; i++) {
//若disSet.length = 15
//第一次外循环当gap=13,则i=13, 14
//第二次外循环当gap=4,则i=4,5,6,7,8,9,10,11,12,13,14
//第三次外循环当gap=1,则i=1,2,3,4,5,6,7,8,9,10,11,12,13,14
temp = disSet[i];
//第一次外循环j=0, 1
//第二次外循环j=0,1,2,3,4,5,6,7,8,9,10,11
//第三次外循环j=0,1,2,3,4,5,6,7,8,9,10,11,12,13
j = i - gap;
//第一次:若d[0].distance > temp.distance = d[13].distance
//...
while (j >= 0 && disSet[j].distance > temp.distance) {
/**
* 若gap=4,i=10,则j=6时的循环为
* 第一圈内循环: temp=disSet[10],如果j=6>0&&disSet[6].distance > temp.distance = disSet[10].distance,则disSet[10] = disSet[6],j=2
* 第二圈内循环: temp=disSet[10],如果j=2>0&&disSet[2].distance > temp.distance = disSet[10].distance,则disSet[6] = disSet[2],j=-2
*/
disSet[j + gap] = disSet[j];
j = j - gap;
}
/**
* 接着上边的例子,小循环之后,j=-2,则j+gap=2,所以disSet[2]=disSet[10]
* 如果在第一圈循环后,就退出循环体,则j=2, j+gap=6,所以disSet[6]=disSet[10]
*/
disSet[j + gap] = temp;
}
//若len=14,则gap=13,4,1
gap = Math.floor(gap / 3);
}
return disSet;
};
let main = (trainSet, testSet, k) => {
let len = trainSet.length,
categoryHash = {
};
disList = [];
for (let i = 0; i < len; i++) {
disList.push(distance(testSet, trainSet[i]));
}
let sortList = shellSort(disList);
let categoryList = sortList.map((s) => s.category).slice(0, k);
categoryHash = countTimes(categoryList);
const sortKNN = Object.keys(categoryHash).sort(function (a, b) {
return categoryHash[b] - categoryHash[a];
});
console.log("It belongs to the category:", sortKNN.length > 0 ? sortKNN[0] : "unknown");
};
/**
* 统计每个元素在all中出现的次数
* @param {[any]} all
*/
function countTimes(all) {
return all.reduce((temps, ele) => {
temps[ele] = temps[ele] ? ++temps[ele] : 1;
return temps;
}, {
});
}
const trainSet = [
[1, 2, "dog"],
[3, 4, "dog"],
[5, 6, "cat"],
[7, 9, "cat"],
[9, 10, "bird"],
[11, 12, "bird"],
[13, 14, "bear"],
[15, 16, "bear"],
[17, 18, "bear"],
[19, 20, "tiger"],
];
const testSet = [3, 9];
main(trainSet, testSet, 5);
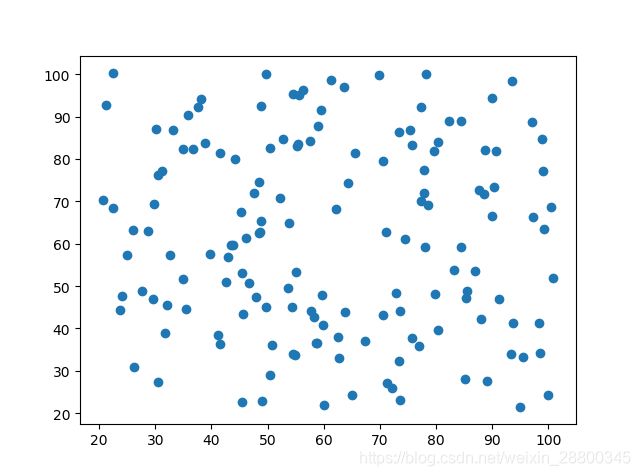
k-means算法
算法过程
- 取k值,假定分为k个簇,并随机取k个聚类中心
- 计算每个样本与这k个中心的距离,将样本划归到最近的中心点
- 计算一次计算的k个类的样本均值,并将该均值作为新的中心
- 重复迭代2-3步骤N次(N自取,尽量大)
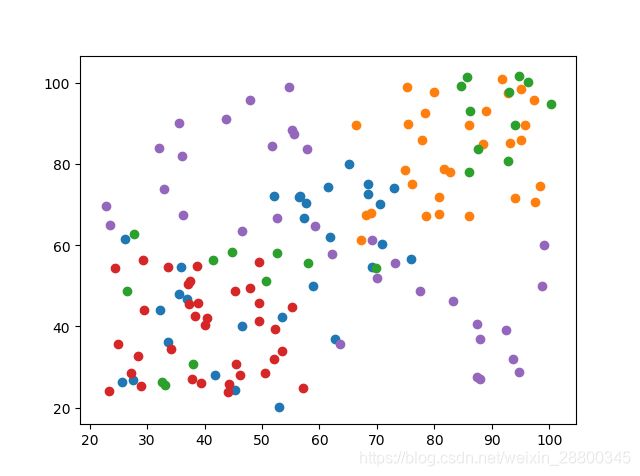
- 输出最终得聚类中心和每个样本所属得类别
代码示例
/**
*计算两点之间的欧氏距离
* @function distance
* @param {[Number, Number]} x
* @param {[Number, Number]} y
* @return {Number} dt
*/
let distance = (x, y) => {
let dt = 0;
for (let i = 0; i < 2; i++) {
dt += (x[i] - y[i]) * (x[i] - y[i]);
}
return Math.sqrt(dt);
};
/**
* 希尔排序,利用插入排序的优点:有序程度越高,效率越高
* @function shellSort
* @param {[Dict]} disSet
* @returns {[Dict]}
*/
let shellSort = (disSet) => {
let len = disSet.length,
j,
temp,
gap = 1;
/**
* gap(n+1) = 3 * gap(n) + 1
* Z变换可解gap为幂次函数
* 设len = 16,则gap = 13, 4, 1
*/
while (gap < len / 3) {
gap = gap * 3 + 1;
}
while (gap > 0) {
for (let i = gap; i < len; i++) {
//若disSet.length = 15
//第一次外循环当gap=13,则i=13, 14
//第二次外循环当gap=4,则i=4,5,6,7,8,9,10,11,12,13,14
//第三次外循环当gap=1,则i=1,2,3,4,5,6,7,8,9,10,11,12,13,14
temp = disSet[i];
//第一次外循环j=0, 1
//第二次外循环j=0,1,2,3,4,5,6,7,8,9,10,11
//第三次外循环j=0,1,2,3,4,5,6,7,8,9,10,11,12,13
j = i - gap;
//第一次:若d[0].distance > temp.distance = d[13].distance
//...
while (j >= 0 && disSet[j].distance > temp.distance) {
/**
* 若gap=4,i=10,则j=6时的循环为
* 第一圈内循环: temp=disSet[10],如果j=6>0&&disSet[6].distance > temp.distance = disSet[10].distance,则disSet[10] = disSet[6],j=2
* 第二圈内循环: temp=disSet[10],如果j=2>0&&disSet[2].distance > temp.distance = disSet[10].distance,则disSet[6] = disSet[2],j=-2
*/
disSet[j + gap] = disSet[j];
j = j - gap;
}
/**
* 接着上边的例子,小循环之后,j=-2,则j+gap=2,所以disSet[2]=disSet[10]
* 如果在第一圈循环后,就退出循环体,则j=2, j+gap=6,所以disSet[6]=disSet[10]
*/
disSet[j + gap] = temp;
}
//若len=14,则gap=13,4,1
gap = Math.floor(gap / 3);
}
return disSet;
};
/**
* 计算离该点距离最小类的索引
* @param {[Number, Number]} x
* @param {[[Number, Number]]} ys
*/
function minDistanceIndex(x, ys) {
let disVector = [];
for (let i = 0; i < ys.length; i++) {
disVector.push({
distance: distance(x, ys[i]), category: i });
}
let sorts = shellSort(disVector);
return sorts[0].category;
}
/**
* 计算坐标(x, y)均值
*/
function mean(array) {
let total = array.length;
let xSum = 0,
ySum = 0;
for (let i = 0; i < total; i++) {
xSum += array[i][0];
ySum += array[i][1];
}
return [xSum / total, ySum / total];
}
/**
* 计算新的质心
* @param {*} categoryDict
*/
function calculateKernal(categoryDict) {
let averages = [];
for (let i = 0; i < Object.keys(categoryDict).length; i++) {
averages.push(mean(categoryDict[i]));
}
return averages;
}
/**
* 迭代更新质心和类
* @param {*} centerPixel
* @param {*} cluster
* @param {*} k
*/
function iterCenterVector(centerPixel, cluster, k) {
//每个点都要计算5次,然后排序,然后选择出该点应该在的类
let resDict = {
};
for (let j = 0; j < k; j++) {
resDict[j] = [];
}
for (let i = 0; i < cluster.length; i++) {
let index = minDistanceIndex(cluster[i], centerPixel);
resDict[index].push(cluster[i]);
}
//计算每一簇的质心
let kernal = calculateKernal(resDict);
return [kernal, resDict];
}
/**
* @function 聚类算法
* @param {[Number]} cluster 原始数据集
* @param {Number} k 聚成k类
* @param {Number} iter 迭代次数
* @param {Number} threshold 阈值
* @returns {Dict}
*/
let kmeans = (cluster, k, iter) => {
let len = cluster.length;
let count = 0,
center = 0,
centerPoint = [];
//初始化k个中心
while (count !== k) {
center = Math.floor(Math.random() * len);
if (centerPoint.indexOf(center) === -1) {
centerPoint.push(center);
count++;
}
}
let centerPixel = centerPoint.map((c) => cluster[c]);
while (iter !== 0) {
//一次更新中心向量
centerPixel = iterCenterVector(centerPixel, cluster, k)[0];
iter--;
}
return iterCenterVector(centerPixel, cluster, k)[1];
};
let cluster = [[37.11,53.49], [22.77,73.11], [61.91,46.52], [57.89,99.08], [65.06,25.68], [44,55.18], [46.5,69.08], [70.49,32.27], [94.67,44.81], [69,74.87], [57.72,35.84],
[68.08,88.39], [93.17,82.72], [86.15,37.96], [86.09,41.41], [87.58,57.93], [100.24,33.16], [38.9,28.44], [40.07,46.14], [36.33,77.43], [54.63,83.23],
[32.16,70.1], [78.53,78.45], [75.27,86.01], [81.62,98.44], [94.12,52.59], [32.96,87.4], [80.76,94.06], [38.67,52.06], [59.3,87.91], [48,93.65],
[52.59,87.93], [66.4,95.16], [43.76,87.34], [55.54,62.22], [51.81,94.8], [84.71,50.76], [52.17,33.61], [35.59,92.46], [29.24,38.41], [70.91,52.89],
[85.61,32.67], [88.95,97.53], [61.54,27.48], [96.24,69.85], [23.56,98.7], [24.9,44.19], [24.43,29.4], [37.53,37.26], [56.53,53.48], [76.19,91.72],
[36.07,63.63], [37.75,49.45], [80.83,92.8], [49.52,52.32], [67.17,97.37], [55.2,69.7], [23.37,57.14], [72.9,45.24], [85.99,79.99], [75.45,77.83],
[47.83,45.26], [69.17,58.85], [92.99,26.47], [68.51,62.74], [57.29,41.9], [55.6,83.79], [60.05,63.56], [75.85,37.02], [61.32,67.37], [56.47,26.12],
[95.82,95.01], [67.95,78.52], [67.41,84.84], [33.6,34.13], [85.04,78.03], [67.06,92.46], [48.6,98.9], [39.43,45.55], [50.59,40.38], [46.18,83.94],
[68.44,35.48], [98.84,89.59], [27.23,28.96], [92.76,27.68], [61.93,40.17], [80.01,26.24], [78.81,74.44], [67.58,71.64], [89.53,98.33], [70.17,43.91],
[101.67,58.42], [92.99,70.69], [70.46,54.49], [49.48,50.4], [33.98,23.84], [93.11,30.85], [77.89,56.39], [51.83,73.75], [44.71,45.83], [83.58,55.61],
[32.66,40.3], [40.53,64.67], [75.06,100.96], [27.99,54.79], [32.03,56.41], [42.43,35.7], [72.08,36.07], [25.78,54.25], [94.87,25.67], [26.96,95.77],
[71.78,97.53], [43.95,51.07], [89.6,58.12], [61.29,95.8], [60.26,20.19], [74.28,26.71], [45.62,27.06], [72.02,42.22], [74.01,24.39], [67.21,97.81],
[54.69,49.96], [99.07,51.09], [32.03,66.56], [89.86,85.9], [101.37,26.37], [41.3,45.7], [100.08,54.34], [39.32,24.11], [36.77,91.1], [75.08,36.79],
[89.47,85.98], [66.74,27.94], [27.47,87.37], [57.93,84.35], [24.88,49.41], [56.56,46.65], [48.81,54.51], [71.88,61.5], [97.61,48.71], [28.79,90.14],
[34.52,26.1], [72.56,47.89], [39.17,65.03], [30.84,28.49], [49.91,82.05], [42.11,28.59], [80.64,62.62], [25.38,55.88], [35.57,88.42]];
console.log(kmeans(cluster, 5, 500));