php算法求出一个数可以被分解成多少个_程序员的算法趣题！

计算机的世界每天都在发生着深刻的变化。新操作系统的发布、CPU性能的提升、智能手机和平板电脑的流行、存储介质的变化、云的普及……这样的变化数不胜数。

在这样日新月异的时代中，“算法”是不变的重要基石。要编写高效率的程序，就需要优化算法。无论开发工具如何进化，熟识并能灵活运用算法仍然是对程序员的基本要求。

本文为那些已经学习过排序、搜索等知名算法，并想要学习更多有趣的算法，进一步提升编程技巧的工程师准备了四道数学谜题形式的问题。这四道趣题分入门、初级、中级、高级，四种级别。

100%的程序员都想挑战这四道有【等级区别】算法趣题。

在挑战之前，先听小编介绍下问题的具体形式：

每个问题大致分为“问题”和“详解”两部分。请各位先通读问题描述，并动手编写程序尝试解题。在这个过程中，具体的实现方法是其次，更重要的是思考“通过哪些步骤来实现才能够解决问题”。每个问题都有思路讲解和源代码示例。请留意自己编程时在处理速度、可读性等方面进行的优化，和本文的源代码示例有什么不同。如果事先看了思路讲解和答案，就会失去解题的乐趣，所以这里建议大家先编程解题，再看讲解。小编为了大家更好的享受解题乐趣，把“详解”和“答案”放在了最后。

准备好了吗？我们开始答题吧！

Q1：入门——尝试用编程解决问题

难度系数：★

优秀的扫地机器人（IQ：80 目标时间：20分钟）

现在有很多制造商都在卖扫地机器人，它非常有用，能为忙碌的我们分担家务负担。不过我们也很难理解为什么扫地机器人有时候会反复清扫某一个地方。

假设有一款不会反复清扫同一个地方的机器人，它只能前后左右移动。举个例子，如果第1 次向后移动，那么连续移动3 次时，就会有以下9 种情况（ 图6 ）。又因为第1 次移动可以是前后左右4 种情况，所以移动3 次时全部路径有9×4 ＝ 36 种。

※ 最初的位置用0 表示，其后的移动位置用数字表示。

问题：

求这个机器人移动12 次时，有多少种移动路径？

Q2：初级——解决简单问题体会算法效果

难度系数：★★

朋友的朋友也是朋友吗（IQ：90 目标时间：25分钟）

“六度空间理论”非常有名。大概的意思是1 个人只需要通过6 个中间人就可以和世界上任何1 个人产生间接联系。本题将试着找出数字的好友（这里并不考虑亲密指数）。

假设拥有同样约数（不包括1）的数字互为“好友”，也就是说，如果两个数字的最大公约数不是1，那么称这两个数互为好友。

从1~N 中任意选取一个“合数”，求从它开始，要经历几层好友，才能和其他所有的数产生联系（所谓的“合数”是指“有除1 以及自身以外的约数的自然数”）。

举个例子，N ＝ 10 时，1~10 的合数是4、6、8、9、10 这5 个。

如果选取的是10，那么10 的好友数字就是公约数为2 的4、6、8这3 个。而9 是6 的好友数字（公约数为3），所以10 只需要经过2 层就可以和9 产生联系（图5 ）。如果选取的是6，则只需经过1 层就可以联系到4、8、9、10 这些数字。因此N ＝ 10 时，无论最初选取的合数是什么，最多经过2 层就可以与其他所有数产生联系。

问题：

求从1~N 中选取7 个合数时，最多经过6 层就可以与其他所有数产生联系的最小的N。

Q3：中级——优化算法实现高速处理

难度系数：★★★

优雅的IP 地址（IQ：100 目标时间：30分钟）

可能大部分读者都清楚，IPv4 中的IP 地址是二进制的32 位数值。不过，这样的数值对我们人类而言可读性比较差，所以我们通常会以8 位为1 组分割，用类似192.168.1.2 这种十进制数来表示它（ 图12 ）。

这里，我们思考一下十进制数0~9 这10 个数字各出现1 次的IP 地址（像正常情况一样，省略每组数字首位的0。也就是说，不能像192.168.001.002 这样表示，而要像192.168.1.2 这样来表示）

问题：

求用二进制数表示上述形式的IP 地址时，能使二进制数左右对称的IP 地址的个数（用二进制数表示时不省略0，用完整的32 位数表示）。

Q4：高级——改变思路让程序速度更快

难度系数：★★★★

异性相邻的座次安排

（IQ：130 目标时间：60分钟）

回想起学生时期调座位的时候，我们的心里总是会小鹿乱撞。想必很多人都对谁会坐自己旁边这件事莫名地激动吧？

这里我们考虑一种“前后左右的座位上一定都是异性”的座次安排。也就是说，像图26 右侧那样，前后左右都是同性的座次安排是不符合要求的（男生用蓝色表示，女生用灰色表示）。

问题：

假设有一个男生和女生分别有15 人的班级，要像图26 那样，排出一个6×5的座次。求满足上述条件的座次安排共多少种（前后或者左右镜像的座次也看作不同的安排。另外，这里不在意具体某个学生坐哪里，只看男生和女生的座次安排）？

答案及解析：Q1-Q4

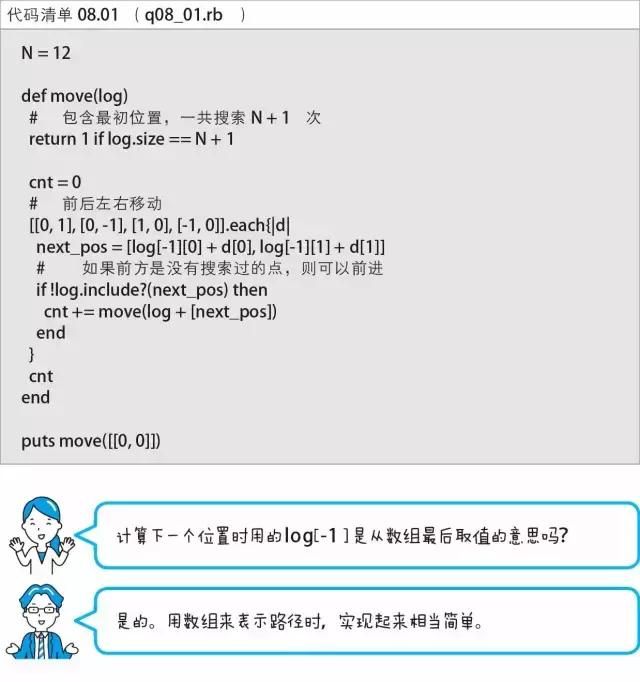
Q1解题思路

用坐标(0, 0) 表示最初的位置。从这个原点开始，避开已经走过的坐标，使机器人前进。用深度优先搜索就可以实现逻辑，如代码清单08.01 所示。

Q1答案

324932种。

——————————————————

Q2解题思路

要解决这个问题，首先要正确理解问题中出现的词。首先是“合数”。

其次是“公约数”这个词。小学的时候，我们就做过求最大公约数的题。公约数的意思就是“共同的约数”。这里，拥有共同约数的数字互为“好友”，那么就需要求最大公约数非1 的情况。

从1~N 中选取7 个合数，且“最多经过6 层”，那么可以得知，我们要找的是“由2 个数相乘得到的数字”的组合。这样的话，乘法运算中的这2 个数就会成为公约数。

举个例子，选出a~h 这些数。简单地说就是，当7 个数字分别是以下的形式时，经过6 层就能与其他所有数产生联系。

a × b, b× c, c× d, d × e, e × f, f× g, g ×h

※这里a~h 这些数字必须“互质”。

Point！

更进一步考虑，也可以像本题中的例子一样，把第1 个数字设置成“平方数”（即4），也就是说变成下面这样的组合更好。

a × a, a × b, b × c, c × d, d × e, e × f, f × g

末尾如果同样设置成平方数就会变得更小，也就是变成下面这样的组合。

a × a, a × b, b × c, c × d, d × e, e × f, f × f

用Ruby 可以像代码清单19.01 这样实现。

Q2答案

55

满足条件的组合为：

[4, 26, 39, 33, 55, 35, 49]

————————————————

Q3解题思路

按照题意，用十进制数表示时要使用0~9 这10 个数字各1 次，那么最高位是除0 以外的9 种情况，而其他各个数位可分别使用0~9 这10个数字各1 次，其排列组合一共9!（9 的阶乘）种，所以总共要遍历9×9! 种，也就是3265920 种情况。

要想求左右对称的二进制数，可以通过把16 位的二进制数逆序排列，并将结果与该16 位的二进制数本身拼合，即生成32 位数来求得。因为是16 位，所以全量搜索时只需要遍历65536 种情况即可。

然后，把这个二进制数转换成十进制数，分别使用0~9 这10 个数字各1 次即可。

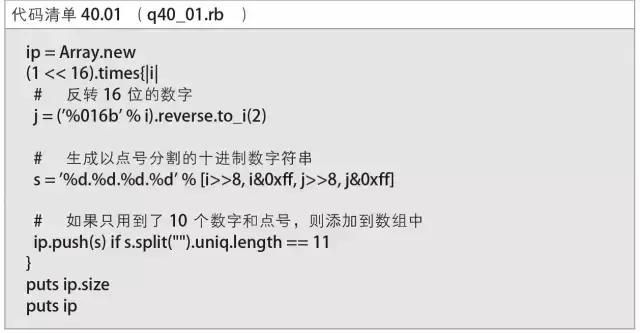
用Ruby 实现时，代码如代码清单40.01 所示。

执行程序可得到正确答案“8”，因而符合条件的IP 地址有8 个，如表4 所示。

Point！

用十进制数表示的时候，如果以点号分割的各部分左右对称，那么整体也就左右对称，因而只需要调查0~255 这些数对应的二进制数中左右对称的数就可以了。也就是说，A.B.C.D 这种形式中，A 要和D 对称，B 要和C 对称。

下面我们试着找出A~D 的各种组合中，0~9 这10 个数字各使用1次的组合。每组（A, D）,（ B, C）生成的IP地址有8 种情况，所以用组合数乘以8 就可以求出结果。

用Ruby 实现时，代码如代码清单40.02 所示。

Q3答案

8个。

————————————————

Q4解题思路

如果完全按照问题描述实现，只需要遍历30 个座位中15 个男生的座次，满足条件就OK 了。如果不考虑可扩展性、处理速度等，只需要把不符合条件的情况排除就可以了，并不是很难。

这里，我们事先准备好要排除的座次安排，统计不在这个范围内的座次安排即可。用Ruby 实现时，如代码清单68.01 所示。

要想改善处理速度，就要考虑“如何缩小搜索范围”。基本的办法不外乎“剪枝”和“内存化”。

这里，我们事先准备前2 排的座次安排，然后生成下一排可能的安排，并递归地搜索下去。同时，把已经搜索过的结果保存到内存中，避免重复搜索（代码清单68.02）。

上面这个程序可以在2 秒左右求出正确答案。

Q4答案

13374192种。

————————————————

最后介绍一下文中出场人物：

《程序员的算法趣题》

作者：增井敏克
1979年生于奈良，毕业于大阪府立大学研究生院。增井IT工程师事务所代表、注册工程师（信息工程学方向）。从事旨在“将商务、数学和IT结合以正确、高效使用计算机”的技能提升指导、软件开发以及信息安全咨询等工作。掌握C/C++、C#、Java、PHP和Ruby等20多种编程语言。著作有《在家就能学会的安全基础》等。目前在面向IT工程师提供业务技能评估服务的平台CodeIQ上负责人气栏目“每周算法”的出题和评审工作。 译者：绝云
毕业于清华软院。曾在日本创意公司KAYAC从事即时通信软件和手游的开发工作，现供职于蚂蚁金服，专攻数据可视化方向。译作有《图解简单算法》《自制编译器》等，曾参与《像外行一样思考，像专家一样实践（修订版）》的审校。

定价：55.00元

• 2016日本IT技术图书大赏获奖作品
• 日本人气算法训练栏目“每周算法”精选辑录
• 140,000程序员挑战过的算法PUZZLE

为什么要读这本书？

本书是一本解谜式的趣味算法书，包含69道数学谜题形式的问题。从实际应用出发，通过趣味谜题的解谜过程，引导读者在愉悦中提升思维能力、掌握算法精髓。

此外，本书作者在谜题解答上，通过算法的关键原理讲解，从思维细节入手，发掘启发性算法新解，并辅以Ruby、JavaScript等不同语言编写的源代码示例，使读者在算法思维与编程实践的分合之间，切实提高编程能力。

更多算法相关书：

http://mp.weixin.qq.com/s/EFdcPaFsYnjKiH9zNDNyzg

目录

第1章　入门篇★尝试用编程解决问题

二进制和十进制

Q01　回文十进制数

Q02　数列的四则运算

Q03　翻牌

Q04　切分木棒

Q05　还在用现金支付吗

Q06　（改版）考拉兹猜想

Q07　日期的二进制转换

Q08　优秀的扫地机器人

Q09　落单的男女

Q10　轮盘的最大值

第2章　初级篇★解决简单问题　体会算法效果

性价比意识

Q11　斐波那契数列

Q12　平方根数字

Q13　有多少种满足字母算式的解法

Q14　世界杯参赛国的国名接龙

Q15　走楼梯

Q16　3根绳子折成四边形

Q17　挑战30人31足

Q18　水果酥饼日

Q19　朋友的朋友也是朋友吗

Q20　受难立面魔方阵

Q21　异或运算三角形

Q22　不缠绕的纸杯电话

Q23　二十一点通吃

Q24　完美的三振出局

Q25　鞋带的时髦系法

Q26　高效的立体停车场

Q27　禁止右转也没关系吗

Q28　社团活动的最优分配方案

Q29　合成电阻的黄金分割比

Q30　用插线板制作章鱼脚状线路

第3章　中级篇★★★优化算法　实现高速处理

时间复杂度记法和计算量

Q31　计算最短路径

Q32　榻榻米的铺法

Q33　飞车与角行的棋步

Q34　会有几次命中注定的相遇

Q35　0和7的回文数

Q36　翻转骰子

Q37　翻转7段码

Q38　填充白色

Q39　反复排序

Q40　优雅的IP 地址

Q41　只用1个数字表示1234

Q42　将牌洗为逆序

Q43　让玻璃杯水量减半

Q44　质数矩阵

Q45　排序交换次数的最少化

Q46　唯一的○×序列

Q47　格雷码循环

Q48　翻转得到交错排列

Q49　欲速则不达

Q50　完美洗牌

Q51　同时结束的沙漏

Q52　糖果恶作剧

Q53　同数包夹

Q54　偷懒的算盘

Q55　平分蛋糕

第4章　高级篇★★★★改变思路　让程序速度更快

编码风格

Q56　鬼脚图中的横线

Q57　最快的联络网

Q58　丢手绢游戏中的总移动距离

Q59　合并单元格的方式

Q60　分割为同样大小

Q61　不交叉, 一笔画下去

Q62　日历的最大矩形

Q63　迷宫会合

Q64　麻烦的投接球

Q65　图形的一笔画

Q66　设计填字游戏

Q67　不挨着坐是一种礼节吗

Q68　异性相邻的座次安排

Q69　蓝白歌会