概念&&介绍
贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解。所以说只有证明局部最优解在全局最优解序列中,才能通过贪心算法得到问题的全局最优解。也就是说选择的贪心策略必须具备无后效性,即某个状态以后的过程不会影响以前的状态,只与当前状态有关。所以对所采用的贪心策略一定要仔细分析其是否满足无后效性。
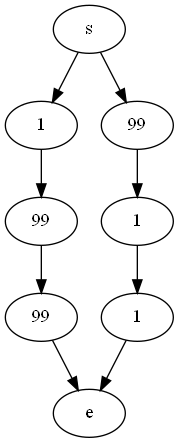
如图0.0所示,我们从$s$点出发到达点$e$,如果我们想要在经过的路径中累计数值最大,我们可以采取在每个分支处选择数值最大的点的贪心策略。但显然我们会选择的$99\rightarrow1\rightarrow1$路径,但实际上正解是路径,这是$1\rightarrow99\rightarrow99$由于我们的选择是具有后效性的,当前选择的点会影响到后面可选择的点,所以会导致我们不能得到全局最优解。
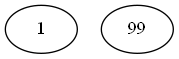
如图0.1所示,我们选择三次,每次从两点中选择一个点并累加它的数值,如果我们想要使累计的数值最大,我们可以选择三次点$99$,并且我们最后得出的解是正解。这是由于我们的选择不具有后效性,当前选择的点并不会影响到后面可选择的点,所以我们可以得到全局最优解。
算法流程
- 把求解的问题分成若干个子问题。
- 对每一子问题求解,得到子问题的局部最优解。
- 把子问题的解局部最优解合成原来解问题的一个解。
适用问题
局部最优策略能导致产生全局最优解。或者将贪心算法进行修改以求出全局最优解
深入理解&&例题
如果前面的两个小例子不能使你透彻地理解贪心算法,那么我们可以来看看下面的几个小例题,通过它们来深入理解贪心算法以及贪心算法使用的场景。
删数问题
读入一个高精度整数$n$,去掉其中$s$个数字后剩下的数字按照原来的次序组成一个新的正整数。寻求一种方案,使得最后组成的数最小。
分析题目,我们可以设计一种贪心策略:进行$s$轮删数,每轮删除最大的一个数,如果数值相同则删除靠前的一个。
我们可以对这个贪心策略进行证明:每轮删除的数字并不会影响后面可删除的数字,因此这种贪心策略不具有后效性,且$s$次删数后剩余所有数字组成的数即为问题的可行解,因此这种贪心策略可行。
#include
using namespace std;
int s,len;
char n[241];
int main(){
cin>>n;
cin>>s;
len=strlen(n);
while(s--){
int p,q;
p=0,q=n[0];
for(int i=1;iq){
q=n[i];
p=i;
}
}//找到目标数
for(int i=p+1;i 均分纸牌
如图3.0所示,有$n$堆纸牌,编号分别为$1,2,3,...,n$。每堆上有若干张,但纸牌总数必为$n$的倍数。可以在任一堆上取若于张纸牌,然后移动。移牌规则:编号为$1$堆上取的纸牌,只能移到编号为$2$的堆上;编号为$n$的堆上取的纸牌,只能移到编号为$n-1$的堆上;其他堆上取的纸牌,可以移到相邻左边或右边的堆上。现在要求找出一种移动方法,用最少的移动次数使每堆上纸牌数都一样多。
分析题目,我们可以得知:要想使移动次数最少,就要把移动的浪费降到最低。例如在相邻的两堆间移动$\ge2$次就是一种浪费,因为这$\ge2$次移动都可以合并成$\le1$次。
因此,我们可以采用移动一次使得一堆牌数达到平均值的贪心策略:先把每堆的牌数减去平均数,然后由左而右的顺序移动纸牌。若第$i$堆纸牌的张数$a[i]$不为$0$,则将值移动到下一堆。如图3.1所示,所有堆的纸牌平均数为$6$,我们可以先将每堆减掉平均数。
然后遍历每堆纸牌,如图3.2所示,纸牌数不为$0$则向下一堆移动,每次移动将移动次数$+1$,最后得到图3.3。
这种贪心策略类似于“把不足平均值的责任推给下一堆,直至多于平均值的纸牌堆来弥补”。通过求解两个纸牌堆之间的最优子解,把所有子解合并得到问题的一个可行解。
#include
using namespace std;
int n,a[101],sum,ans;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
sum+=a[i];
}
sum/=n;
for(int i=1;i<=n;i++){
a[i]-=sum;
}
for(int i=1;i<=n;i++){
if(a[i]!=0){
a[i+1]+=a[i];
ans++;
}
}
printf("%d\n",ans);
return 0;
} 糖果传递
有$n$个小朋友坐成一圈,每人有$a[i]$个糖果。每人只能给左右两人传递糖果。每人每次传递一个糖果代价为$1$。求使所有人获得均等糖果的最小代价。
和均分纸牌类似,现在假设编号为$i$的人初始有$a[i]$个糖果。对于$1$号来说,他给了$n$号$x[1]$个糖果,还剩$a[1]-x[1]$个;但是因为$2$号给了他$x[2]$个糖果,所以最后还剩$a[1]-x[1]+x[2]$个糖果。根据题设,该金币数等于$m$。换句话说,我们得到了一个方程:$m=a[1]-x[1]+x[2]$。
同理,对于第$2$个人,有$m=a[2]-x[2]+x[3]$。最终,我们可以得到$n$个方程,一共$n$个变量,是不是可以直接解方程组了呢?很可惜,还不行。因为从前$n-1$个方程可以推导出最后一个方程。所以,实际上只有$n-1$个方程是有用的。
尽管无法直接解出答案,我们还是可以尝试着用$x[1]$表示出其他的$x[i]$,则本题就变成了单变量的极值问题。
对于第$1$个人,$a[1]-x[1]+x[2]=m\rightarrow x[2]=m-a[1]+x[1]=x[1]-c[1]$(令$c[1]=a[1]-m$,下面类似)
对于第$2$个人,$a[2]-x[2]+x[3]=m\rightarrow x[3]=m-a[2]+x[2]=2m-a[1]-a[2]+x[1]=x[1]-c[2]$($c[2]=c[1]+a[2]-m$)
对于第$3$个人,$a[3]-x[3]+x[4]=m\rightarrow x[4]=m-a[3]+x[3]=3m-a[1]-a[2]-a[3]+x[1]=x[1]+c[3]$
......
对于第$1$个人,$a[n]-x[n]+x[1]=m$。这是一个多余的等式,并不能给我们更多的信息。我们希望所有的$x[i]$的绝对值之和尽量小,即$|x[1]|+|x[1]-c[1]|+|x[1]-c[2]|+...+|x[1]-c[n]-1|$要最小。注意到$|x[i]-c[i]|$的集合意思是数轴上点$x[i]$到$c[i]$的距离,所以问题变成了:给定数轴上的$n$个点,找出一个到它们的距离之和尽量小的点。
结论:给定数轴上的$n$个点,在数轴上的所有点中,中位数离所有顶点的距离之和最小。凡是能转化为这个模型的题目都可以用中位数求解。
#include
#define maxn 1000001
using namespace std;
int n,a[maxn];
long long c[maxn],sum,ans;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]),sum+=a[i];
}
sum/=n;
for(int i=1;i<=n;i++){
c[i]+=sum-a[i]+c[i-1];
}
sort(c+1,c+n+1);
int mid=c[n/2];
for(int i=1;i<=n;i++){
ans+=abs(mid-c[i]);
}
printf("%lld",ans);
return 0;
} 进阶习题
- 洛谷 P1223 排队接水 题目链接
- 洛谷 P1803 凌乱的yyy / 线段覆盖 题目链接
- 洛谷 P3817 小A的糖果 题目链接
- 洛谷 P1478 陶陶摘苹果(升级版)题目链接
- 洛谷 P5019 铺设道路 题目链接
- 洛谷 P1208 混合牛奶 题目链接
- 洛谷 P1094 纪念品分组 题目链接
- 洛谷 P1090 合并果子 题目链接
- 洛谷 P4447 分组 题目链接
- 洛谷 P1080 国王游戏 题目链接
- POJ P3262 Protecting the Flowers 题目链接
- POJ P1716 Integer Intervals 题目链接
参考资料
- 贪心算法 百度百科
- 贪心策略取得最优解的条件_常用算法之贪心算法 CSDN @weixin_39799825
- 贪心算法的最优解条件 CSDN @逆羽飘扬
- 贪心算法-例题讲解 博客园 @In'f