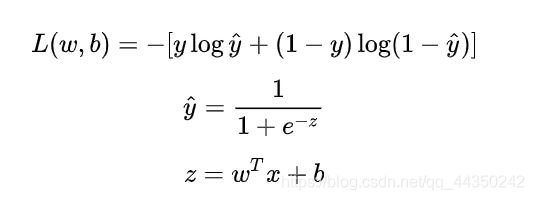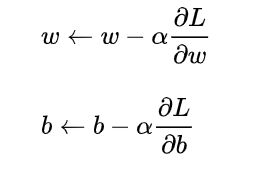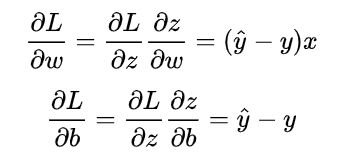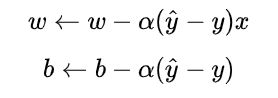机器学习(超详细讲解):利用Logistic Regression(逻辑回归)实现多分类
机器学习:利用Logistic Regression(逻辑回归)实现多分类
文章目录
- 机器学习:利用Logistic Regression(逻辑回归)实现多分类
-
- 1.Logistic Regression的引入
- 2.损失函数
- 3.梯度下降法
- 4.参数更新
- 5 多分类器介绍
-
-
- 5.1 一对一分类器(OvO)
- 5.1 一对其余分类器(OvR)
-
- 6 Python实战(Iris数据集准确率93%)
-
- 6.1 读取数据集(划分训练集和测试集)
- 6.2 二分类任务
- 6.3 采用OVO方式训练多分类器
- 6.4 测试模型准确率
- 7.完整代码
本文章利用逻辑回归来实现多分类问题,对于大部分数据集,其准确率可以达到90%以上。
源代码和数据集点此
1.Logistic Regression的引入
在介绍Logistic Regression(对数几率回归)之前,我们先来介绍Liner Regression(线性回归),简单的来说,线性回归的目标就是要寻找合适的W和B使得式1.1的误差最小。对于误差,我们可以使用损失函数来衡量。对于W和B的寻找,我们可以使用牛顿迭代法,梯度下降法等,后面我们将重点介绍梯度下降法。
Z = W T X + B Z=W^TX+B Z=WTX+B
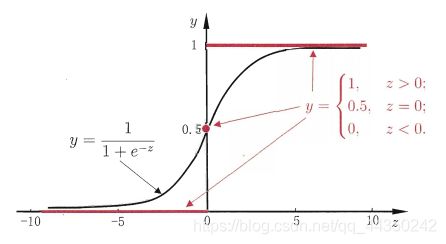
对于Logistic Regression而言,我们要完成二分类任务,实际上就是要在线性模型输出的基础上,将输出Z映射到两个区域内,比如我们可以将输出映射为数字 0 或 1,那么我们就可以将输出为 0 的作为一类,输出为 1 的作为另一类,这样就完成了二分类任务。那么我们应该选择什么样的函数作为Z的映射函数呢?最简单的我们可以选择单调越阶函数:
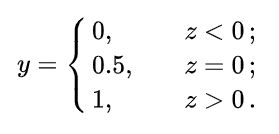
当线性模型输出Z<0时,将其映射为 0 ;当输出Z>0时,将其映射为 1;输出Z=0时不做处理。但是单调越阶函数的数学性质并不好(譬如单调性,连续性,可导性等)。故我们选择Sigmoid函数作为映射函数,Sigmoid函数具有非常好的数学性质。
2.损失函数
谈到机器学习,首要目标是要确定损失函数,对于Logistic Regression,我们选用如下式子作为损失函数( y ^ \hat{y} y^为推测值, y {y} y为实际值):
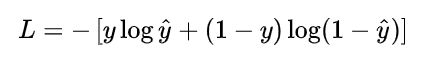
我们不难发现当实际值 y {y} y 为 0 时,推测值 y ^ \hat{y} y^ 越接近真实值 0 ,函数L的值越小;当实际值 y {y} y为 1 时,推测值 y ^ \hat{y} y^越接近真实值1,函数L的值越小。由此可见,函数L可以作为损失函数。
3.梯度下降法
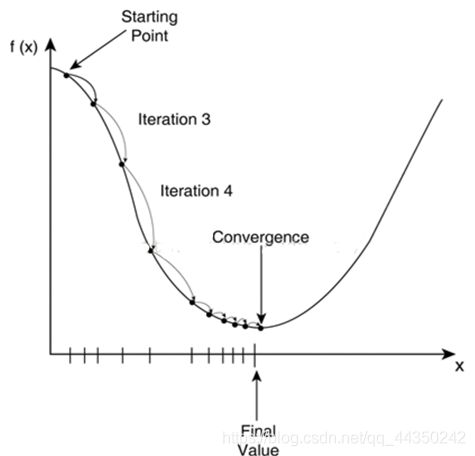
梯度下降法的目标是寻找函数的最小值。其本质为不断调整参数 x 使得代价函数 f (x) 取得最小值。从直观上理解,就是在碗状结构的凸函数上取一个初始值,然后挪动这个值一步步靠近最低点的过程。从数学上理解,为了找到最小值点,就应该朝着下降速度最快的方向(导函数/偏导方向)迈进,每次迈进一小步,再看看此时的下降最快方向是哪,再朝着这个方向迈进,直至最低点。
对于函数上的某一点而言,导函数/偏导数的方向为其下降最快的方向,故我们每次向导函数的方向迈出一小步,至于这一步有多小取决于我们设定的学习率 α \alpha α。
4.参数更新
确定损失函数后,我们就要思考如何利用损失函数来更行优化参数值W和B,损失函数本质上是随着W和B变化的函数:
现在我们的问题转化为寻找合适的w和b,使得函数L(w,b)的值最小,这就将问题转化为一个二元函数的最小值问题了,对于二元函数的最小值问题,我们采用已经介绍过的梯度下降法,于是我们可以得到参数更新公式:
对于上诉式子作进一步推导:
于是参数更新公式变成:
即下一次的参数 = 上一次的参数 减去 学习率 x 输入 x 误差
至此,我们可以利用上诉结论来实战操作
5 多分类器介绍
已经介绍了如何通过Logistic Regression进行二分类,但我们的目标是解决多分类问题,自然而然,想到用多个二分类器去构建多分类器。在构建多分类模型时,我们介绍两种方法,一对一策略(OvO)和一对其余策略(OvR),在Python实战中,我们将用到OvO。
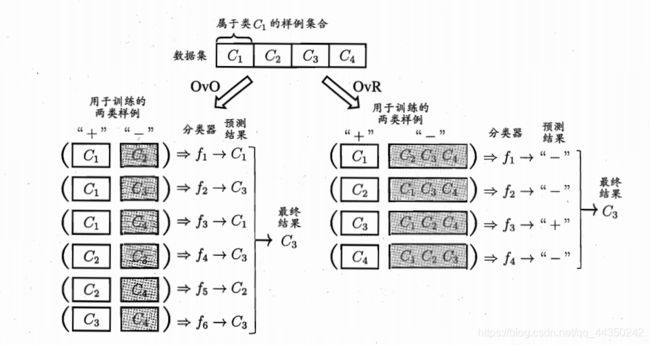
5.1 一对一分类器(OvO)
对于OvO策略,我们将训练样本中的 N 个类别两两配对,从而产生 N(N-1)/2 个分类任务(如上图左所示)。我们每次拿其中的两类去训练一个分类器,最终将训练出 N(N-1)/2 个分类器。当预测一组数据时,分别用这 N(N-1)/2个分类器进行预测,最终的结果为所有预测结果中最多的那一个(即投票选出结果)。
5.1 一对其余分类器(OvR)
对于OvR策略,枚举每一种类别,将枚举到的类别作为正例而其他的统一作为反例,这样只需要训练 N N N 个分类器(如上图右所示)。当预测一组数据时,分别用这 N N N 个分类器进行预测,选取结果为正例 (只可能有一个为正例) 的类别作为最终结果。
6 Python实战(Iris数据集准确率93%)
源代码和数据集点此
6.1 读取数据集(划分训练集和测试集)
def getdata():
# 读取数据集 并且把数据集分为测试集和训练集,奇数项为测试集,偶数项为训练集
dataSet = []
labels = []
f = open('watermelon_3a.csv')
flag = 1 # 设置flag来跳过第一行
for line in f.readlines():
if(flag == 1):
flag = 0
continue
str_data = line.strip().split(",")[1:]
labels.append(str_data[-1])
for k in range(len(str_data)-1):
str_data[k] = float(str_data[k])
str_data.insert(0, 1.0)
dataSet.append(str_data)
train_data = []
test_data = []
train_label = []
dataset = dataSet
# 归一化处理优点:1.加快求解速度 2.可能提高精度
for j in range(1, len(dataset[0])-1):
l_sum = 0
all_sum = 0
for i in range(len(dataset)):
l_sum += dataset[i][j]
# 计算期望
average = l_sum/len(dataset)
# 计算标准差
for i in range(len(dataset)):
all_sum += pow(dataset[i][j]-average, 2)
standard_deviation = math.sqrt(all_sum/(len(dataset)-1))
# 对每列数据进行归一化,减均值,除方差
for i in range(len(dataset)):
dataset[i][j] = (dataset[i][j]-average)/standard_deviation
for i in range(len(dataSet)):
if i % 2 == 0:
train_data.append(dataSet[i])
train_label.append(labels[i])
else:
test_data.append(dataSet[i])
#返回参数中,dataSet为全部数据,便于西瓜数据集画图,train_data为训练集,test_data为数据集
return dataSet, labels, train_data, test_data, train_label
6.2 二分类任务
def get_weight(data, label):
matrix_data = mat(data) # m行n列
matrix_label = mat(label).transpose() # m行
m, n = shape(matrix_data)
learn_rate = 0.00001 # 学习率
max_cycles = 60000 # 迭代次数
weights = ones((n, 1)) # 初始化权值矩阵
# 利用梯度下降法进行权重更新
for k in range(max_cycles):
estimate_result = sigmoid(matrix_data*weights)
error = matrix_label-estimate_result
weights = weights+learn_rate*matrix_data.transpose()*error
return weights
6.3 采用OVO方式训练多分类器
最 终 的 训 练 结 果 形 式 : [ [ 分 类 器 1 ] , [ 分 类 器 2 ] , [ 分 类 器 3 ] . . . ] 最终的训练结果形式:[ [分类器1],[分类器2],[分类器3]...] 最终的训练结果形式:[[分类器1],[分类器2],[分类器3]...]
def train_model(data, labels):
# 最终的训练结果形式:[ [分类器1],[分类器2],[分类器3]...]
# 把第i类作为正类,其他作为负类
result_weight = []
uniqueVals = list(set(labels))
for i in range(len(uniqueVals)):
for k in range(i+1, len(uniqueVals)):
train_data = []
train_label = []
for j in range(len(data)):
if(data[j][-1] == uniqueVals[i]):
train_label.append(1.0)
train_data.append(data[j][:-1])
elif(data[j][-1] == uniqueVals[k]):
train_label.append(0.0)
train_data.append(data[j][:-1])
re = get_weight(train_data, train_label).tolist()
re.append(uniqueVals[i])
re.append(uniqueVals[k])
result_weight.append(re)
return result_weight
6.4 测试模型准确率
def predict(pre_data, result_weight, label):
pre_data = mat(pre_data)
uniqueVals = list(set(label))
result = []
for i in range(len(result_weight)):
estimate_result = sigmoid(pre_data*mat(result_weight[i][:-2]))
if(estimate_result >= 0.5):
# 正例
result.append(result_weight[i][-2])
else:
# 反例
result.append(result_weight[i][-1])
return get_mostfeature(result)
def test_rate(test_data):
postive = 0
total = len(test_data)
for i in range(total):
pre_data = test_data[i][:-1]
result = predict(pre_data, result_weight, train_label)
if(result == test_data[i][-1]):
postive = postive+1
return postive/total
7.完整代码
import matplotlib.pyplot as plt
import numpy as np
import time
from numpy import *
# 定义sigmoid函数
def sigmoid(n):
return 1.0/(1+exp(-n))
def getdata():
# 读取数据集 并且把数据集分为测试集和训练集,奇数项为测试集,偶数项为训练集
dataSet = []
labels = []
f = open('watermelon_3a.csv')
flag = 1 # 设置flag来跳过第一行
for line in f.readlines():
if(flag == 1):
flag = 0
continue
str_data = line.strip().split(",")[1:]
labels.append(str_data[-1])
for k in range(len(str_data)-1):
str_data[k] = float(str_data[k])
str_data.insert(0, 1.0)
dataSet.append(str_data)
train_data = []
test_data = []
train_label = []
dataset = dataSet
# 归一化处理优点:1.加快求解速度 2.可能提高精度
for j in range(1, len(dataset[0])-1):
l_sum = 0
all_sum = 0
for i in range(len(dataset)):
l_sum += dataset[i][j]
# 计算期望
average = l_sum/len(dataset)
# 计算标准差
for i in range(len(dataset)):
all_sum += pow(dataset[i][j]-average, 2)
standard_deviation = math.sqrt(all_sum/(len(dataset)-1))
# 对每列数据进行归一化,减均值,除方差
for i in range(len(dataset)):
dataset[i][j] = (dataset[i][j]-average)/standard_deviation
for i in range(len(dataSet)):
if i % 2 == 0:
train_data.append(dataSet[i])
train_label.append(labels[i])
else:
test_data.append(dataSet[i])
#返回参数中,dataSet为全部数据,便于西瓜数据集画图,train_data为训练集,test_data为数据集
return dataSet, labels, train_data, test_data, train_label
def get_mostfeature(lt):
index1 = 0 # 记录出现次数最多的元素下标
max = 0 # 记录最大的元素出现次数
for i in range(len(lt)):
flag = 0 # 记录每一个元素出现的次数
for j in range(i+1, len(lt)): # 遍历i之后的元素下标
if lt[j] == lt[i]:
flag += 1 # 每当发现与自己相同的元素,flag+1
if flag > max: # 如果此时元素出现的次数大于最大值,记录此时元素的下标
max = flag
index1 = i
return lt[index1]
def get_weight(data, label):
matrix_data = mat(data) # m行n列
matrix_label = mat(label).transpose() # m行
m, n = shape(matrix_data)
learn_rate = 0.00001 # 学习率
max_cycles = 60000 # 迭代次数
weights = ones((n, 1)) # 初始化权值矩阵
# 利用梯度下降法进行权重更新
for k in range(max_cycles):
estimate_result = sigmoid(matrix_data*weights)
error = matrix_label-estimate_result
weights = weights+learn_rate*matrix_data.transpose()*error
return weights
# 训练分类器
def train_model(data, labels):
# 把第i类作为正类,其他作为负类
result_weight = []
uniqueVals = list(set(labels))
for i in range(len(uniqueVals)):
for k in range(i+1, len(uniqueVals)):
train_data = []
train_label = []
for j in range(len(data)):
if(data[j][-1] == uniqueVals[i]):
train_label.append(1.0)
train_data.append(data[j][:-1])
elif(data[j][-1] == uniqueVals[k]):
train_label.append(0.0)
train_data.append(data[j][:-1])
re = get_weight(train_data, train_label).tolist()
re.append(uniqueVals[i])
re.append(uniqueVals[k])
result_weight.append(re)
return result_weight
def predict(pre_data, result_weight, label):
pre_data = mat(pre_data)
uniqueVals = list(set(label))
result = []
for i in range(len(result_weight)):
estimate_result = sigmoid(pre_data*mat(result_weight[i][:-2]))
if(estimate_result >= 0.5):
# 正例
result.append(result_weight[i][-2])
else:
# 反例
result.append(result_weight[i][-1])
return get_mostfeature(result)
def test_rate(test_data):
postive = 0
total = len(test_data)
for i in range(total):
pre_data = test_data[i][:-1]
result = predict(pre_data, result_weight, train_label)
if(result == test_data[i][-1]):
postive = postive+1
return postive/total
print("开始时间:", time.strftime("%Y-%m-%d %H:%M:%S", time.localtime()))
# 获取训练集
all_data, all_labels, train_data, test_data, train_label = getdata()
print("训练中...")
# 训练模型
result_weight = train_model(train_data, train_label)
print("训练成功!训练结果为:", result_weight)
print("正在测试准确率...")
# 预测
rate = test_rate(test_data)
print("准确率:", rate)
ticks2 = time.time()
print("结束时间:", time.strftime("%Y-%m-%d %H:%M:%S", time.localtime()))
'''
#画图,只有西瓜数据集(二维)才能画图,大于二维的数据集不能画图
weights = train_model(all_data, all_labels)
data_arr=array(all_data)
p=shape(data_arr)[0]
#print(p)
x1=[]
y1=[]
x2=[]
y2=[]
for i in range(p):
if int(all_labels[i])==1:
x1.append(float(data_arr[i,1]))
y1.append(float(data_arr[i,2]))
else:
x2.append(float(data_arr[i,1]))
y2.append(float(data_arr[i,2]))
fig=plt.figure()
ax=fig.add_subplot(111)
ax.scatter(x1,y1,s=30,c='red',marker='s')
ax.scatter(x2,y2,s=30,c='green')
x=arange(-1.5,1.5,0.1)
# print(x)
y=(-weights[0][0][0]-weights[0][1][0]*x)/weights[0][2][0]
ax.plot(x,y)
plt.show()
'''