基于python利用熵权法计算数据权重——一个简单的图形用户界面编程

简介

师弟又催我给他公众号写文了，这次还点名要这个题目……所以我就先到自己的博客里写写练练手……
（下面是正式的简介）
根据信息熵的定义，对于某项指标，可以用熵值来判断某个指标的离散程度，其信息熵值越小，指标的离散程度越大， 该指标对综合评价的影响（即权重）就越大，如果某项指标的值全部相等，则该指标在综合评价中不起作用。因此，可利用信息熵这个工具，计算出各个指标的权重，为多指标综合评价提供依据。
（上段直接拷贝自百度百科）

技术流程

参考相关的文献，我们知道要做熵值法赋权，首先要进行标准化，把所有指标的数据拉到一个尺度然后才有对比的价值。因此，第一步就是对数据进行标准化处理。在此之上，我们第二步再开始进行熵值法的赋权计算。
（其实本来应该分三步的，即第一步是数据标准化，第二步是求各指标信息熵，第三步是求各指标权重，但是由于之前写代码我把后两部合并了，所以……两步到位吧……）
然后，基于这个技术流程，我们会写两个GUI。为什么是两个呢，因为我其他工作也用到了数据标准化处理，所以我把数据标准化处理的GUI单独写了一个（我的锅）。

数据

我拿我上上篇文章（基于python的机器学习回归：可视化、预测及预测结果保存（附代码））的数据删掉target就当作这次的实验示范数据吧！
数据长下面这个样子：

一共551行，共计550条数据，10个指标：

然后我们的目的就是算出这10个指标的熵权，熵权总和必须为1。

代码：极差标准化

又到了喜闻乐见的代码部分。
首先，我们先写一个极差标准化的代码，预处理一下我们的数据。（这边就不多介绍极差标准化了，看了公式就明白什么意思了）

import tkinter as tk
from tkinter.filedialog import *
from tkinter.messagebox import *
import xlrd
import xlwt



# 极差标准化部分
##########1.读取Excel文件##########
def load_data(FilePath,ExcelSheet):
    workbook = xlrd.open_workbook(str(FilePath))       #excel路径
    sheet = workbook.sheet_by_name(ExcelSheet)             #sheet表
    return sheet

##########2.极差标准化运算########
def normalization(sheet,StartCol,EndCol,StartRow,EndRow,ConverseCol,SavePath):           #起始列，终止列，起始行，终止行，逆向指标所在列（列表格式），保存路径
    #######创建一个workbook########
    workbook = xlwt.Workbook(encoding = 'utf-8')    # 创建一个workbook 设置编码
    worksheet = workbook.add_sheet('Sheet')    # 创建一个worksheet
    #######读取行列，并计算极差标准化值#######
    for j in range(StartCol-1,EndCol):         #获取列代码
        Cols = sheet.col_values(j)
        #ColsName = Cols[0]         #获取列名并删除
        del Cols[0]            #删除列名
        ColsMax = max(Cols)                  #获取整列的最大值，最小值
        ColsMin = min(Cols)
        ExtremeSub = ColsMax - ColsMin         #计算极差
        for i in range(StartRow-1,EndRow):       #获取行代码
            PreValue = sheet.cell(i,j).value     #获取对应行列单元格里数据
            Value = (PreValue-ColsMin)/ExtremeSub
            for Conve in ConverseCol:           #计算逆向指标
                if j == Conve-1:       #如果是逆向指标列，采用另一种计算方法
                    Value = (ColsMax-PreValue)/ExtremeSub   #逆向指标值计算
            worksheet.write(i , j , label=Value)             #写入对应单元格
    workbook.save(str(SavePath))      #保存



# GUI相关函数
# 初始文件路径
def Get_FilePath():
	file_get = askopenfilename()  # 选择打开什么文件，返回文件名
	file_path.set(file_get)             # 设置变量filename的值

# 获取保存路径
def Get_SavePath():
	save_get = asksaveasfilename(defaultextension='.xls')   # 设置保存文件，并返回文件名，指定文件名后缀为.xls
	save_path.set(save_get)             # 设置变量filename的值

# 极差标准化执行模块
def exe_norma():
	try:
		Sheet = load_data(str(file_path.get()),str(read_sheet_name.get()))          #读取Sheet
		normalization(Sheet,int(start_col.get()),int(end_col.get()),int(start_row.get()),int(end_row.get()),eval(converse_col.get()),
		str(save_path.get()))          #极差标准化与保存Sheet
		#从上面读取的sheet，起始列，终止列，起始行，终止行，逆向指标所在列（列表格式），保存路径
		showinfo(title='执行完毕', message=f'极差标准化计算成功，结果保存在{str(save_path.get())}')
	except:
		showwarning(title='执行出错', message='无法执行极差标准化计算，请检查所输入的信息')



# GUI界面部分
root = tk.Tk()
root.title('极差标准化工具')
root.geometry('800x380')
file_path = tk.StringVar()
save_path = tk.StringVar()

# 选择文件、获取路径
tk.Label(root, text='选择文件：').place(x=10,y=20)
tk.Entry(root, textvariable=file_path, width=90).place(x=80,y=20)
tk.Button(root, text='打开文件', command=Get_FilePath).place(x=730,y=15)

# 读取的sheet名称
tk.Label(root, text='读取sheet：').place(x=10,y=70)
read_sheet_name = tk.Entry(root, width=90)
read_sheet_name.place(x=80,y=70)

# 起始、终止行列
tk.Label(root, text='起始列：').place(x=10,y=120)
start_col = tk.Entry(root, width=13)
start_col.place(x=80,y=120)
tk.Label(root, text='终止列：').place(x=190,y=120)
end_col = tk.Entry(root, width=13)
end_col.place(x=260,y=120)
tk.Label(root, text='起始行：').place(x=370,y=120)
start_row = tk.Entry(root, width=13)
start_row.place(x=440,y=120)
tk.Label(root, text='终止行：').place(x=550,y=120)
end_row = tk.Entry(root, width=13)
end_row.place(x=620,y=120)

# 逆向指标所在列
tk.Label(root, text='逆向指标列：').place(x=10,y=170)
converse_col = tk.Entry(root, width=30)
converse_col.place(x=80,y=170)
tk.Label(root, text='用中括号"[ ]"括起，列号用英文输入下的逗号","分隔，如无逆向指标输入"[]"').place(x=310,y=170)

# 保存路径
tk.Label(root, text='保存路径：').place(x=10,y=220)
tk.Entry(root, textvariable=save_path, width=90).place(x=80,y=220)
tk.Button(root, text='选择目录', command=Get_SavePath).place(x=730,y=215)

# 运行按钮
tk.Button(root, text='开始进行极差标准化计算', command=exe_norma, width=30, height=2).place(x=290,y=280)

root.mainloop()

之前的文章里代码我一般不会解释的，更何况这里我们写的是GUI~都在注释里惹。
想直接用的朋友们可以直接拷贝，然后运行就行了（只要该有的import包你都有，基本上没有什么问题）。
运行出来会出现一个界面，长这个样子：

剩下具体的操作在后面再说。

代码：熵权法赋权

与上一节相同，这里仍然是GUI界面，所以我直接贴代码。
把代码拷贝到另一个.py文件里运行就行了。

import tkinter as tk
from tkinter.filedialog import *
from tkinter.messagebox import *
import xlrd
import xlwt
from math import log



# 熵值法处理数据部分
##########1.读取Excel文件##########
def load_data(FilePath,ExcelSheet):
    workbook = xlrd.open_workbook(str(FilePath))       #excel路径
    sheet = workbook.sheet_by_name(ExcelSheet)             #sheet表
    return sheet

##########2.熵值法运算########
def get_entropy(sheet,StartCol,EndCol,StartRow,EndRow,SavePath):           #起始列，终止列，起始行，终止行，保存路径
    #######创建一个workbook########
    workbook = xlwt.Workbook(encoding = 'utf-8')    # 创建一个workbook 设置编码
    worksheet = workbook.add_sheet('Sheet')    # 创建一个worksheet
    ######获取样本数和指标数######
    m = EndCol+1-StartCol       #指标数
    n = EndRow+1-StartRow       #样本数
    ColBlank = StartCol - 1     #前面的空列数
    #####获取计算熵值法需要的元素#######
    AbovePartList = []
    LCLSBVS = []
    for j in range(StartCol-1,EndCol):         #获取列代码
        ColLSBV = []
        Cols = sheet.col_values(j)
        #ColsName = Cols[0]         #获取列名并删除
        del Cols[0]            #删除列名
        EachSampleInThisIndicatorSum = sum(Cols)   #每个样本的该列指标求和
        for i in range(StartRow-1,EndRow):
            PreValue = sheet.cell(i,j).value
            if PreValue == 0:
                PreValue = 0.000000001
            LnSumBracketVar = (PreValue/EachSampleInThisIndicatorSum) * log(PreValue/EachSampleInThisIndicatorSum)
            ColLSBV.append(LnSumBracketVar)
        ColLSBVSum = sum(ColLSBV)       #计算括号内的和
        LnCLSBVS = ColLSBVSum / log(n)   #除以 ln(n)
        LCLSBVS.append(LnCLSBVS)
    #########熵值法公式上下部分######
        AbovePart = 1 + LnCLSBVS       #上半部分
        AbovePartList.append(AbovePart)   #把上半部分存为列表
    LCLSBVSSum = sum(LCLSBVS)
    BelowPart = m + LCLSBVSSum         #下半部分固定值
    ##########写入#############
    for j in range(0,m):     #指标数
        Value = AbovePartList[j] / BelowPart    #值等于上半部分除以下半部分
        worksheet.write(StartRow-1 , j+ColBlank , label=Value)   #写入
    workbook.save(str(SavePath))      #保存



# GUI相关函数
# 初始文件路径
def Get_FilePath():
	file_get = askopenfilename()  # 选择打开什么文件，返回文件名
	file_path.set(file_get)             # 设置变量filename的值

# 获取保存路径
def Get_SavePath():
	save_get = asksaveasfilename(defaultextension='.xls')   # 设置保存文件，并返回文件名，指定文件名后缀为.xls
	save_path.set(save_get)             # 设置变量filename的值

# 极差标准化执行模块
def exe_norma():
	try:
		Sheet = load_data(str(file_path.get()),str(read_sheet_name.get()))          #读取Sheet
		get_entropy(Sheet,int(start_col.get()),int(end_col.get()),int(start_row.get()),int(end_row.get()),
        str(save_path.get()))          #极差标准化与保存Sheet
		#从上面读取的sheet，起始列，终止列，起始行，终止行，逆向指标所在列（列表格式），保存路径
		showinfo(title='执行完毕', message=f'熵值法处理数据成功，结果保存在{str(save_path.get())}')
	except:
		showwarning(title='执行出错', message='无法执行熵值计算，请检查所输入的信息')



# GUI界面部分
root = tk.Tk()
root.title('熵值法处理工具')
root.geometry('800x330')
file_path = tk.StringVar()
save_path = tk.StringVar()

# 选择文件、获取路径
tk.Label(root, text='选择文件：').place(x=10,y=20)
tk.Entry(root, textvariable=file_path, width=90).place(x=80,y=20)
tk.Button(root, text='打开文件', command=Get_FilePath).place(x=730,y=15)

# 读取的sheet名称
tk.Label(root, text='读取sheet：').place(x=10,y=70)
read_sheet_name = tk.Entry(root, width=90)
read_sheet_name.place(x=80,y=70)

# 起始、终止行列
tk.Label(root, text='起始列：').place(x=10,y=120)
start_col = tk.Entry(root, width=13)
start_col.place(x=80,y=120)
tk.Label(root, text='终止列：').place(x=190,y=120)
end_col = tk.Entry(root, width=13)
end_col.place(x=260,y=120)
tk.Label(root, text='起始行：').place(x=370,y=120)
start_row = tk.Entry(root, width=13)
start_row.place(x=440,y=120)
tk.Label(root, text='终止行：').place(x=550,y=120)
end_row = tk.Entry(root, width=13)
end_row.place(x=620,y=120)

# 保存路径
tk.Label(root, text='保存路径：').place(x=10,y=170)
tk.Entry(root, textvariable=save_path, width=90).place(x=80,y=170)
tk.Button(root, text='选择目录', command=Get_SavePath).place(x=730,y=165)

# 运行按钮
tk.Button(root, text='开始进行熵值法处理计算', command=exe_norma, width=30, height=2).place(x=290,y=230)

root.mainloop()

运行了也会出现一个界面，长这个样子：

具体的操作依然在后面。

实验操作与流程

首先，我们现在手上已经get到数据了。是一个10个指标的，550条的数据集合（10列，550行）。把这个数据的excel文件放在我们找得到的地方。
然后打开极差标准化GUI的代码，运行之。把该写的信息写上。如下图：

选择文件，点右边的打开文件然后找到你的文件双击就行了。
读取sheet，就是看你excel里sheet的名称是什么。
起始列终止列，就是你的指标列，我们是10个指标，并且从第1列放到第10列，所以写1和10就行。
起始行终止行，就是你数据条，因为第一行是label，所以我们就从2开始到551。
逆向指标列，就是那种值越小最后的数值越好的指标（相反我们常用的正向指标列是值越大越好）。比如说我之前做的一个城市评价体系，其中有一个是人口老龄化占比，这个就是典型的逆向指标；而什么城镇人口，GDP这些就是正向指标。因为实验中我们没逆向指标，所以就直接填[]；如果有的话，比如第4列第5列是逆向指标，那么我们填[4, 5]
保存路径，就是你要保存的位置，这个打开方式和选择文件一样。
最后，我们点击下面的大按钮“开始进行极差标准化计算”。就会出现这么一个窗口：

到它说的这个位置，就会看到一个新的excel。打开它，大概长这样：

同样是10列，550行，只不过这里我们第一行没了label。这个就是我们数据的极差标准化后的结果，两个excel单元格是一一对应的。
然后我们接下来打开熵权法赋权的GUI的.py文件，运行之。与上面一样，填上该填的信息。如下图：

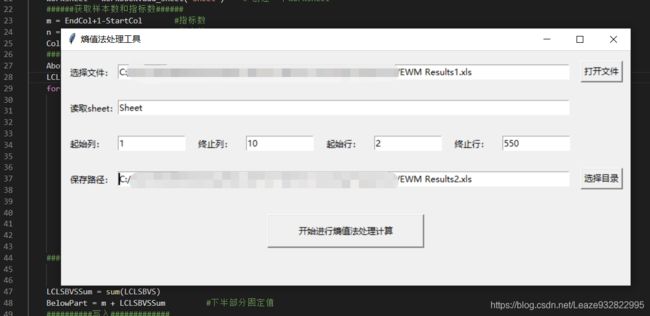
选择文件，我们就选我们极差标准化处理后的文件（一定不要选到一开始那个数据文件，不然权重会出错的！！！）。
读取sheet，填入sheet名。
起始列终止列，起始行终止行，和前面一样。
保存路径，这个计算后就是最终的结果了，选一个你找得到的想保存的路径。
最后，点击下面的“开始运行熵值法处理计算”。弹出这么一个窗口：

打开生成的excel文件，这个就是它的权重了。

然后我们把一开始的那个数据的label贴上去，并且求和看看：

一一对应！破费科特！

关于数据获取

虽然这篇文章用到的样本集数据获取是免费的，但是还是球球大家让我恰点钱吧QAQ~（二维码在下面）。
需要数据的小伙伴们可以在csdn私信我或者联系我邮箱（[email protected]）。虽然但是，还是建议大家邮箱联系，因为亲测csdn私信的bug还挺多的……

另外我及不及时回复比较随缘了，我尽量一天看一次邮箱。

希望大家能打赏支持一下（我的乞讨码在下面）~
-----------------------分割线（以下是乞讨内容）-----------------------