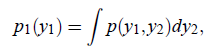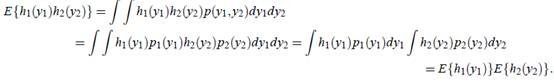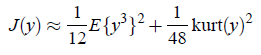ICA扩展描述
7. ICA算法扩展描述
上面介绍的内容基本上是讲义上的,与我看的另一篇《Independent Component Analysis:
Algorithms and Applications》(Aapo Hyvärinen and Erkki Oja)有点出入。下面总结一下这篇文章里提到的一些内容(有些我也没看明白)。
首先里面提到了一个与“独立”相似的概念“不相关(uncorrelated)”。Uncorrelated属于部分独立,而不是完全独立,怎么刻画呢?
第二个不相关的条件要比第一个独立的条件“松”一些。因为独立能推出不相关,不相关推不出独立。
证明如下:
反过来不能推出。
比如,![]() 和
和![]() 的联合分布如下(0,1),(0,-1),(1,0),(-1,0)。
的联合分布如下(0,1),(0,-1),(1,0),(-1,0)。
上面提到过,如果![]() 是高斯分布的,A是正交的,那么
是高斯分布的,A是正交的,那么![]() 也是高斯分布的,且
也是高斯分布的,且![]() 与
与![]() 之间是独立的。那么无法确定A,因为任何正交变换都可以让
之间是独立的。那么无法确定A,因为任何正交变换都可以让![]() 达到同分布的效果。但是如果
达到同分布的效果。但是如果![]() 中只有一个分量是高斯分布的,仍然可以使用ICA。
中只有一个分量是高斯分布的,仍然可以使用ICA。
那么ICA要解决的问题变为:如何从x中推出s,使得s最不可能满足高斯分布?
中心极限定理告诉我们:大量独立同分布随机变量之和满足高斯分布。
我们一直假设的是![]() 是由独立同分布的主元
是由独立同分布的主元![]() 经过混合矩阵A生成。那么为了求
经过混合矩阵A生成。那么为了求![]() ,我们需要计算
,我们需要计算![]() 的每个分量
的每个分量![]() 。定义
。定义![]() ,那么
,那么![]() ,之所以这么麻烦再定义z是想说明一个关系,我们想通过整出一个
,之所以这么麻烦再定义z是想说明一个关系,我们想通过整出一个![]() 来对
来对![]() 进行线性组合,得出y。而我们不知道得出的y是否是真正的s的分量,但我们知道y是s的真正分量的线性组合。由于我们不能使s的分量成为高斯分布,因此我们的目标求是让y(也就是
进行线性组合,得出y。而我们不知道得出的y是否是真正的s的分量,但我们知道y是s的真正分量的线性组合。由于我们不能使s的分量成为高斯分布,因此我们的目标求是让y(也就是![]() )最不可能是高斯分布时的w。
)最不可能是高斯分布时的w。
那么问题递归到如何度量y是否是高斯分布的了。
一种度量方法是kurtosis方法,公式如下:
如果y是高斯分布,那么该函数值为0,否则绝大多数情况下值不为0。
但这种度量方法不怎么好,有很多问题。看下一种方法:
负熵(Negentropy)度量方法。
我们在信息论里面知道对于离散的随机变量Y,其熵是
连续值时是
在信息论里有一个强有力的结论是:高斯分布的随机变量是同方差分布中熵最大的。也就是说对于一个随机变量来说,满足高斯分布时,最随机。
定义负熵的计算公式如下:
也就是随机变量y相对于高斯分布时的熵差,这个公式的问题就是直接计算时较为复杂,一般采用逼近策略。
这种逼近策略不够好,作者提出了基于最大熵的更优的公式:
之后的FastICA就基于这个公式。
另外一种度量方法是最小互信息方法:
这个公式可以这样解释,前一个H是![]() 的编码长度(以信息编码的方式理解),第二个H是y成为随机变量时的平均编码长度。之后的内容包括FastICA就不再介绍了,我也没看懂。
的编码长度(以信息编码的方式理解),第二个H是y成为随机变量时的平均编码长度。之后的内容包括FastICA就不再介绍了,我也没看懂。
8. ICA的投影追踪解释(Projection Pursuit)
投影追踪在统计学中的意思是去寻找多维数据的“interesting”投影。这些投影可用在数据可视化、密度估计和回归中。比如在一维的投影追踪中,我们寻找一条直线,使得所有的数据点投影到直线上后,能够反映出数据的分布。然而我们最不想要的是高斯分布,最不像高斯分布的数据点最interesting。这个与我们的ICA思想是一直的,寻找独立的最不可能是高斯分布的s。
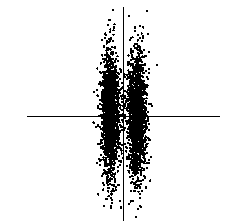
在下图中,主元是纵轴,拥有最大的方差,但最interesting的是横轴,因为它可以将两个类分开(信号分离)。
9. ICA算法的前处理步骤
1、中心化:也就是求x均值,然后让所有x减去均值,这一步与PCA一致。
2、漂白:目的是将x乘以一个矩阵变成![]() ,使得
,使得![]() 的协方差矩阵是
的协方差矩阵是![]() 。解释一下吧,原始的向量是x。转换后的是
。解释一下吧,原始的向量是x。转换后的是![]() 。
。
其中使用特征值分解来得到E(特征向量矩阵)和D(特征值对角矩阵),计算公式为
下面用个图来直观描述一下:
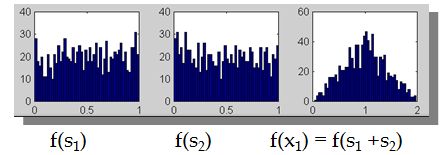
假设信号源s1和s2是独立的,比如下图横轴是s1,纵轴是s2,根据s1得不到s2。
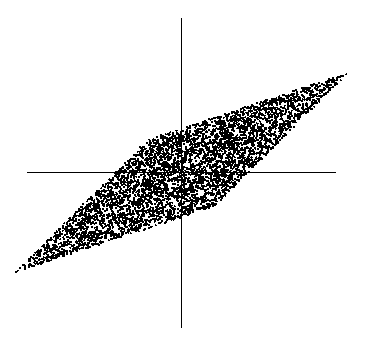
我们只知道他们合成后的信号x,如下
此时x1和x2不是独立的(比如看最上面的尖角,知道了x1就知道了x2)。那么直接代入我们之前的极大似然概率估计会有问题,因为我们假定x是独立的。
因此,漂白这一步为了让x独立。漂白结果如下:
然而这时x分布很好的情况下能够这样转换,当有噪音时怎么办呢?可以先使用前面提到的PCA方法来对数据进行降维,滤去噪声信号,得到k维的正交向量,然后再使用ICA。
10. 小结
ICA的盲信号分析领域的一个强有力方法,也是求非高斯分布数据隐含因子的方法。从之前我们熟悉的样本-特征角度看,我们使用ICA的前提条件是,认为样本数据由独立非高斯分布的隐含因子产生,隐含因子个数等于特征数,我们要求的是隐含因子。
而PCA认为特征是由k个正交的特征(也可看作是隐含因子)生成的,我们要求的是数据在新特征上的投影。同是因子分析,一个用来更适合用来还原信号(因为信号比较有规律,经常不是高斯分布的),一个更适合用来降维(用那么多特征干嘛,k个正交的即可)。有时候也需要组合两者一起使用。这段是我的个人理解,仅供参考。