基于安全多方计算(MPC)的隐私计算技术(一)

前面文章讲到了通过可信执行环境(TEE，Trusted Execution Environment)技术可以达到隐私计算的目的。

TEE是通过硬件的方式保护参与计算数据的隐私性，但基于TEE的隐私计算并不是建立在参与方间完全无信任环境下的，实际上会有一个各参与方都认可的可信根，一般而言，这个可信根是TEE的制造厂商。

现在比较成熟的TEE技术就是英特尔的SGX，如果是通过SGX做隐私计算，由于要去英特尔的服务器上做远程认证，则需要各个参与方都信任英特尔。因此基于TEE的隐私计算对于某些安全性要求更高场景并不适用。

除了基于TEE的隐私计算外，安全多方计算技术（MPC或SMPC，Secure multi-party computation）也可以做隐私计算。安全多方计算技术则是基于密码学的多种技术纯软件实现的隐私计算。各参与方之间无需可信根，更加安全。但由于包含了复杂的密码学操作，相较于基于TEE的隐私计算而言，效率会低一些。

安全多方计算简介

安全多方计算是指在无可信第三方的情况下，多个参与方协同计算一个约定的函数，并且保证每一方仅获取自己的计算结果，无法通过计算过程中的交互数据推测出其他任意一方的输入和输出数据（除非函数本身可以由自己的输入推测出其他参与方的输入和输出）。

安全多方计算可抽象概括为数学模型，其公式如下：

安全多方计算于1986 年由姚期智院士通过姚氏百万富翁问题提出：两个百万富翁街头邂逅，他们都想炫一下富，比一比谁更有钱，但是出于隐私，都不想让对方知道自己到底拥有多少财富，如何在不借助第三方的情况下，让他们知道谁更有钱。姚氏“百万富翁问题”后经发展，成为现代密码学中非常活跃的研究领域，即安全多方计算。
安全多方计算组成

安全多方计算技术并不是一个单一的技术，它本身是由一些列技术组成的协议栈。按层次可为2层，如下图所示：

支撑技术层

支撑技术层提供构建MPC的基础技术实现，包含常用的加密解密、hash函数、密钥交换、同态加密（HE，Homomorphic Encryption）、伪随机函数等，还包含MPC中的基础工具：秘密分享（SS，Secret Sharing）、不经意传输协议(OT，Oblivious Transfer)、不经意为随机函数（OPRF，Oblivious Pseudorandom Function）等；

具体MPC算法层

具体MPC算法是利用支撑技术组合构造的MPC协议。

构造的MPC协议又分为两大类，专用算法和通用框架。

专用算法是指为解决特定问题所构造出的特殊MPC协议，由于是针对性构造并进行优化，专用算法的效率会比基于混淆电路（GC ，Garbled Circuit）的通用框架高很多，包含四则运算，比较运算，矩阵运算，隐私集合求交集，隐私数据查询，差分隐私等等；

通用框架是指可以满足大部分计算逻辑的通用MPC协议，主要基于混淆电路实现，可将计算逻辑编译成电路，然后混淆执行，支持大部分计算逻辑，但对于复杂计算逻辑，混淆电路的效率会有不同程度的降低。

专用算法和通用框架是解决隐私计算问题的两种不同思路，专用算法为特定隐私计算逻辑设计，效率更高，但只能支持单一计算逻辑；通用框架可以支持大部分隐私计算逻辑，由于支持更多的计算逻辑，与专用算法相比效率会有很大的差距（约10~100倍）。

安全多方计算基础技术

秘密分享

秘密分享（SS，Secret Sharing）是指数据拆散成多个无意义的数，并将这些数分发到多个参与方那里。每个参与方拿到的都是原始数据的一部分，一个或少数几个参与方无法还原出原始数据，只有把各自的数据凑在一起时才能还原出真实数据。

秘密分享的一种经典方案，1979年Shamir提出了阈值秘密分享方案，该方案支持n个参与方中的任意t个可以联合解开秘密数据，具体方案如下：

秘密分享技术本身可以直接构造安全多方计算协议，在计算时，各参与方将自己的输入数据通过秘密分享的方式将数据的分片分发到各参与方，各参与方用自己收到的每个数据分片进行计算，并且在适当的时候交换一些数据（交换的数据本身看起来也是随机的，不包含关于原始数据的信息），将计算结束后的结果发到发起方，发起方将所有参与方返回的结果进行聚合。

通过基于数据分片进行计算，可以保护每个参与方的输入，但在最后聚合时，可以还原出真实的计算结果。

Shamir的阈值秘密分享是线性的，即满足加法同态，因此可以通过该方案实现多方加法运算。接下来介绍通过Shamir的阈值秘密分享三方求和。

假设三方A，B，C分别有数据a，b，c，有数据需求方想要计算a+b+c。

不经意传输
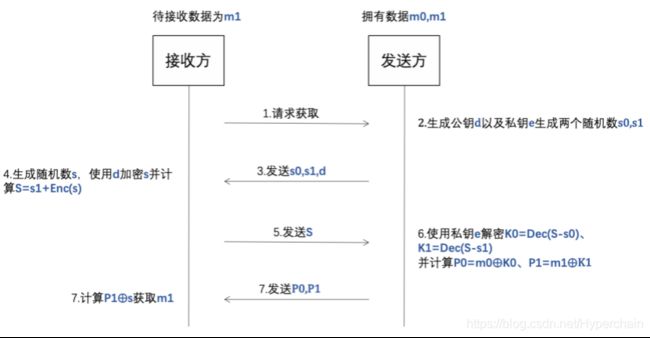
不经意传输(OT，Oblivious Transfer)是指数据发送方有n个数据，数据接收方接收其中的一个数据，且数据接收方不能获取其他的数据，数据发送方不知道接收方选择接收的数据具体是哪一个。

接下来介绍“2选1”的OT方案：

混淆电路

混淆电路（GC，Garbled Circuit）是指将一参与方安全多方计算协议的计算逻辑编译成布尔电路，然后将布尔电路中的每一个门进行加密并打乱加密顺序完成混淆操作。

完成混淆后，该参与方将加密电路以及与其输入相关的标签（另一方无法从标签中反推输入的信息）发送给另一参与方。另一方（作为接收方）通过不经意传输(OT)按照其输入选取标签，并在此基础上对混淆电路进行解密获取计算结果。

假设两个参与方A和B的输入分别是x（0），y（1），计算逻辑是与门


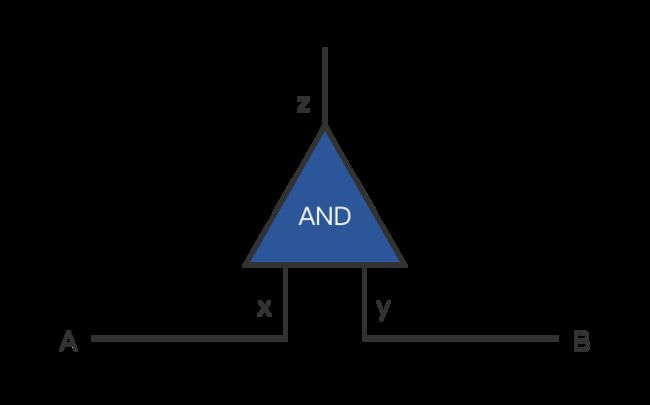
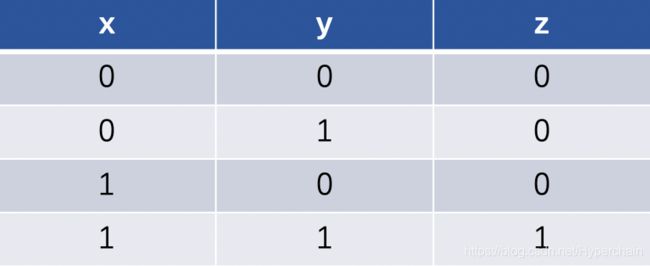
真值表

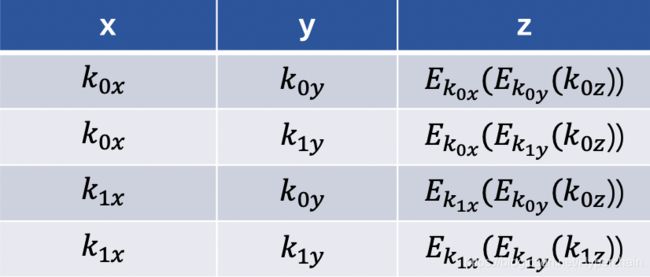
加密后真值表

整个过程中通过OT协议，A无法感知B的输入，通过加密输出并打乱顺序，B无法知道A的输入。

由于大部分计算逻辑都可以表示成布尔电路或算术电路，因此基于混淆电路技术可以构造出通用的安全多方计算协议。

同态加密

同态加密（HE，Homomorphic Encryption）是指对密文计算后的结果再解密和直接对明文计算的结果一致，同态加密按照其满足的运算类型可分为加法同态（Paillier同态加密），乘法同态（RSA同态加密），以及加法乘法都满足的全同态加密（Gentry同态加密）。

通过同态加密也可以直接构造安全多方计算协议。每个参与方的输入数据都通过同态加密后发送给计算方，计算方在本地基于密文进行计算，将计算结果返回各需求方并解密获得真实的计算结果。由于各参与方的输入都是加密后进行计算，可以保证各参与方输入的隐私性。

接下来介绍一种通过Paillier加法同态实现三方加法的方案。

假设两方A，B，C分别有数据a，b，c，有数据需求方想要获取a+b+c。

1. 数据需求方基于Paillier算法生成公私钥对（Pk，Sk），并将Pk发给A，B，C。

2. A，B，C分别使用收到的公钥加密a，b，c。然后B，C分别将Enc(b)， Enc©发送给A。

3. A收到Enc(b)，Enc©后计算Enc(a)+Enc(b)+Enc©= Enc(a+b+c)，并将计算后的结果发送给数据需求方。

4. 数据需求方解密收到的数据，获取a+b+c。

Dec(Enc(a)+Enc(b)+Enc©)=Dec(Enc(a+b+c))=a+b+c

总结

本文介绍了安全多方计算的整体技术体系以及用于构造安全多方计算协议的基础技术。

通过安全多方计算技术可以很好的解决各机构间不愿共享数据，不敢共享数据的问题，在保证各方数据安全的前提下，进行多方数据的联合计算，可以在一定程度上打消各机构共享私密数据的顾虑，愿意共享出自己的数据，联合挖掘数据价值，拓宽数据的使用维度。

作者简介
刘敬
数据网格实验室算法工程师
致力于研究MPC通用和专用算法