一起学python-opencv三（numpy数组广播和一些其它操作）

numpy广播

 

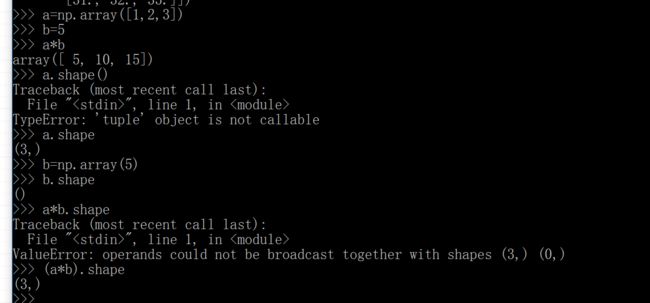
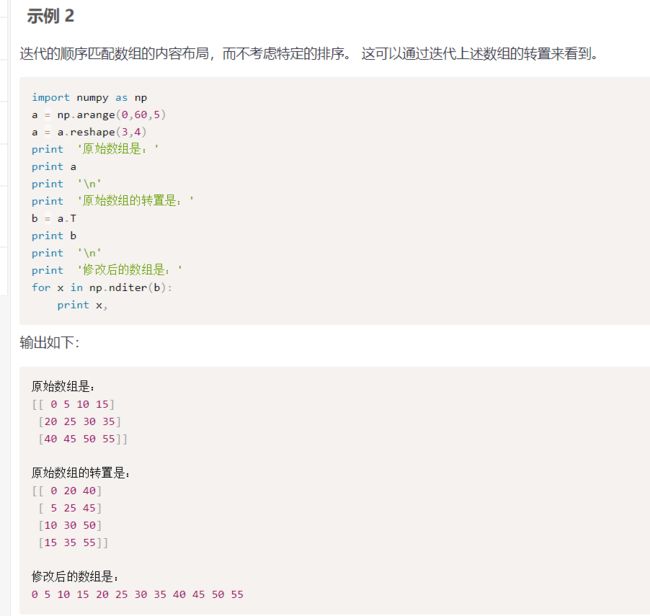
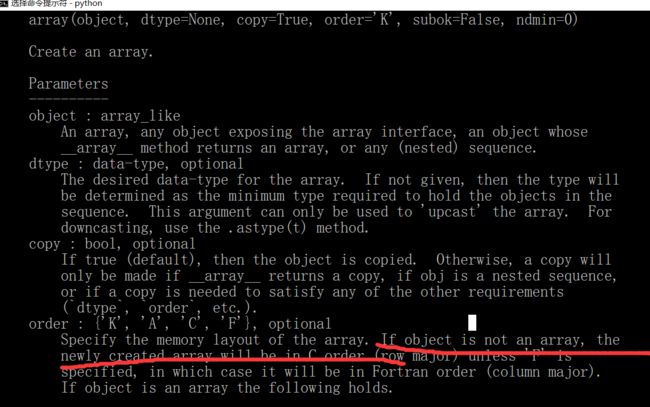
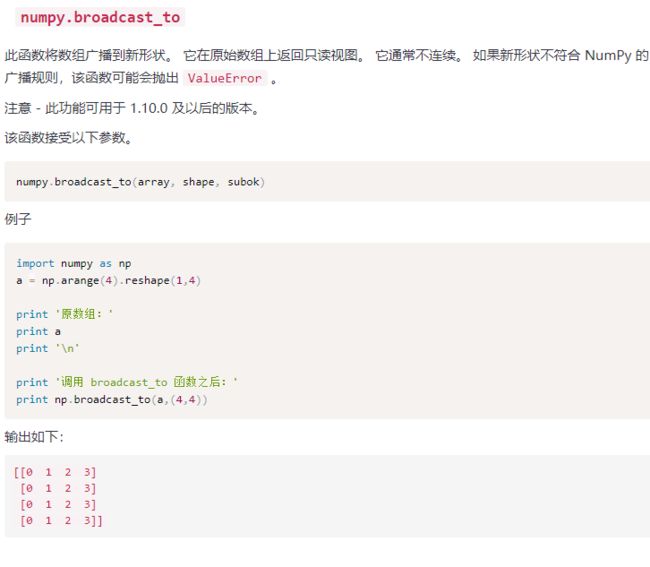
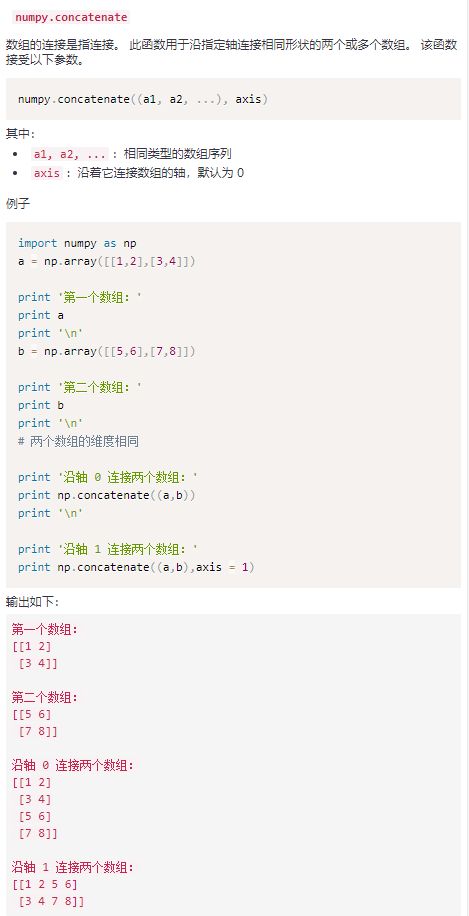
看上面的叙述还是有点懵，因为我感觉它是机器翻译过来的。还是得实际试验体会，先看一看提供的例子：

 

 

 

这个例子我们看到了，就是要把维度小的强行扩充到和维度大的数组一样的维度。上面的图示还是比较清晰地展示了这个过程。这个乘号有点像MATLAB里的.*，这种运算都是对元素而言的，不是按照我们在线性代数里面学的矩阵的运算法则。不过我们需要再看点别的资料：参考了https://www.cnblogs.com/yangmang/p/7125458.html。

 

这个例子用的IDE是anaconda自带的一个spider软件。感觉这个说的还不是很清楚，又参考了https://blog.csdn.net/yangnanhai93/article/details/50127747

 

 

 

 

 

a的shape是(3,)补齐之后是（1，3）也就是一行三列，为什么在前面补呢？因为规则里面写着啊。

 

b.shape是()，补齐之后是（1，1），根据规则二，最后输出的维度应该是(1,3)，shape显示的是（3，）。

 

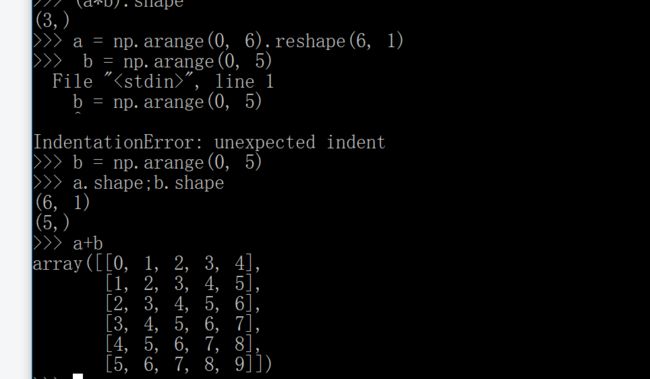
这个(5,)会补成（1，5），然后根据规则二，最后的输出是(6,5)。

 

这个是(3,)补成了(1,3)，最后结果是(4,3)。我就不再试了，这个还是二维的。下面来理解一下三维的情况。

 

 

 

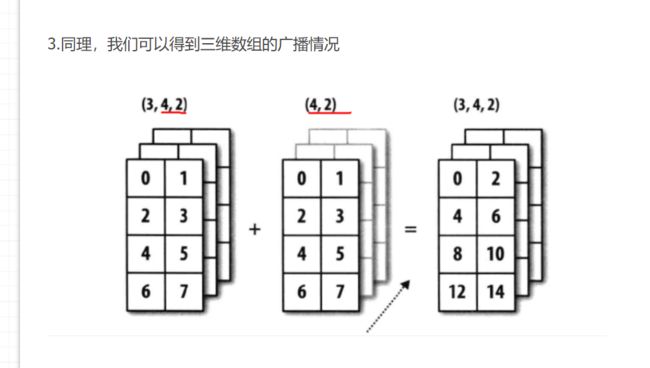
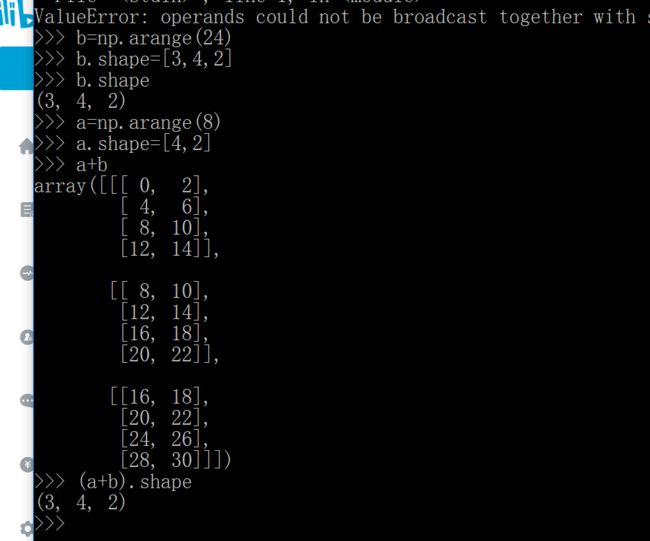
对于这个，我的理解是这样的，(4,2)会补成（1，4，2），然后就可以广播了。

那么看了这么多资料，我总结一下：

1. shape补全法则：统一把两个数组的维度补全为ndim大的数组的，如果不够，shape要在前面补1，注意不是后面补1，是前面。

2. 广播法则：两个数组能发生广播的条件是：两个数组的按照补全法则的shape完全一样（当然其实这个就不叫广播了）或者不一样的维度对应的值必须有一个是1。

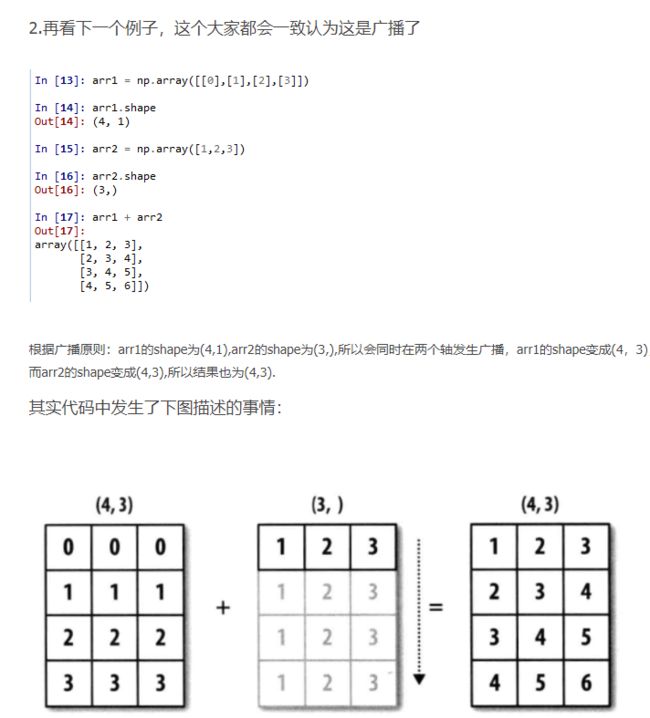
借用一下别人的例子：

 

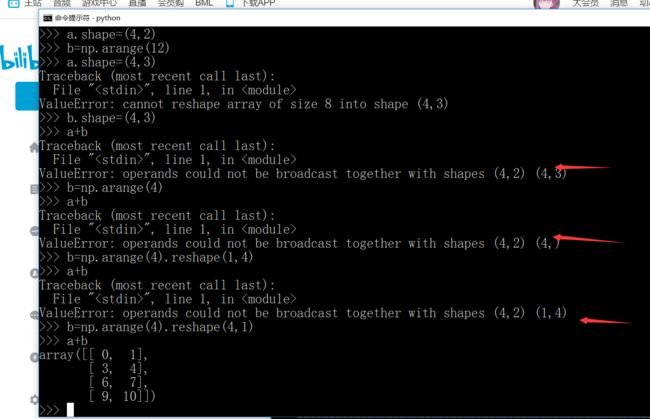
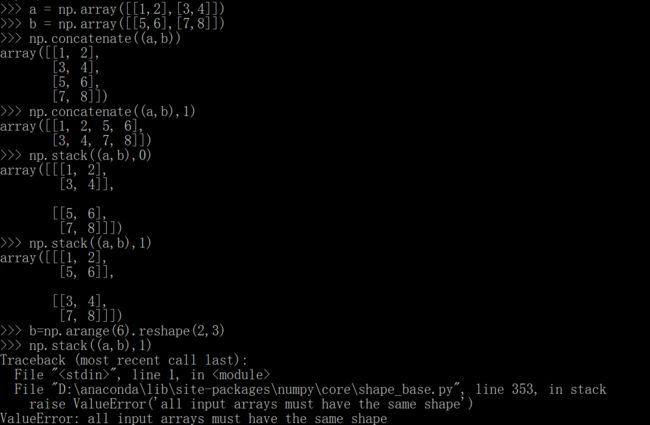
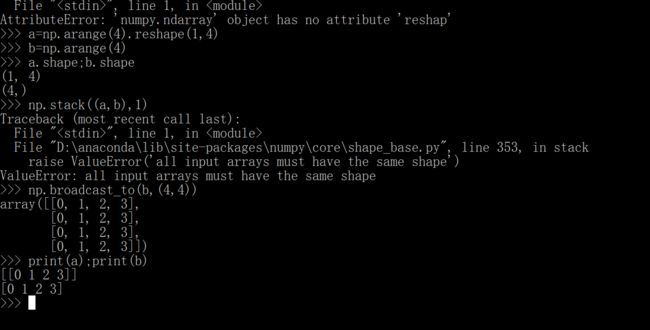
第一次出错时因为(4,3)和(1,4)肯定不行啊，主要原因是在第二个维度的3和4，既不一样，又没有一个是1，第二次（4，3）和(4,1)肯定没问题啊，因为4一样，第二个维度虽然不一样但是又一个是1。再举一个例子：

 

(4,2)和（4，3）是因为2和3不一样，(4,2)和(4,)是因为补全之后是(4,2)和(1,4)主要原因事2和4不相等，又没有1，最后(4,2)和(4,1)成功是因为1和2虽然不一样，但是有1。

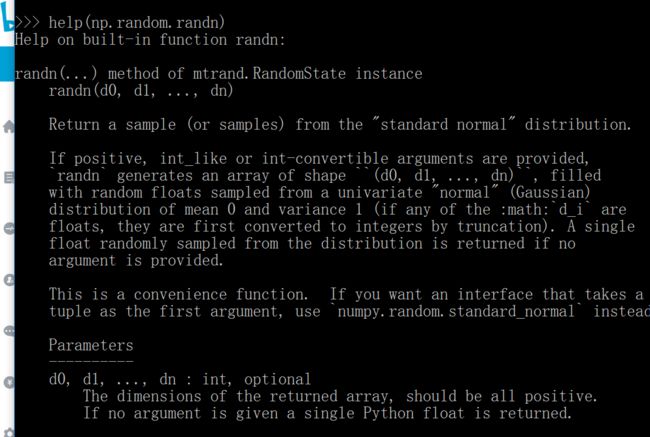
上面有一些np的函数,np.random.randn。

 

 

 

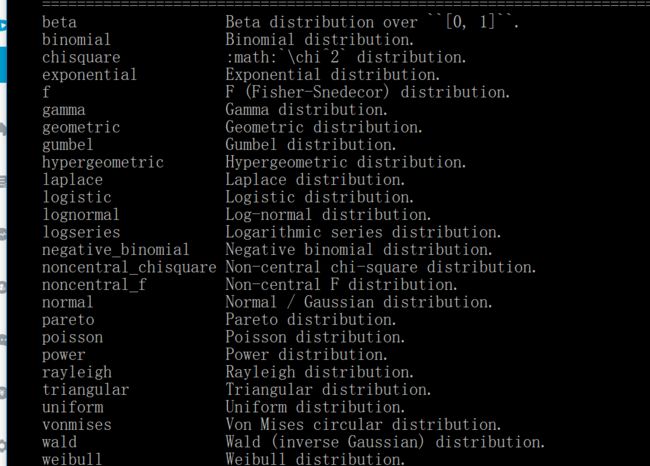
这个randn是根据标准正态分布来产生随机数的，n就是normal的意思，正态分布也叫高斯分布。这个函数MATLAB里面也有，python的random模块好像也有。不加n的，也就是rand就是平均分布，randint就是平均整数分布。还有很多种分布：binomial是二项式分布。exponential是指数分布。

 

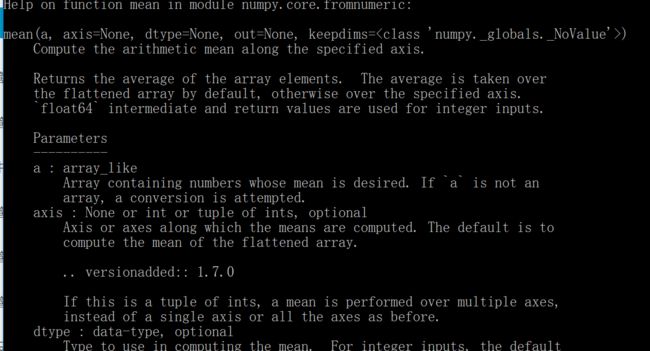
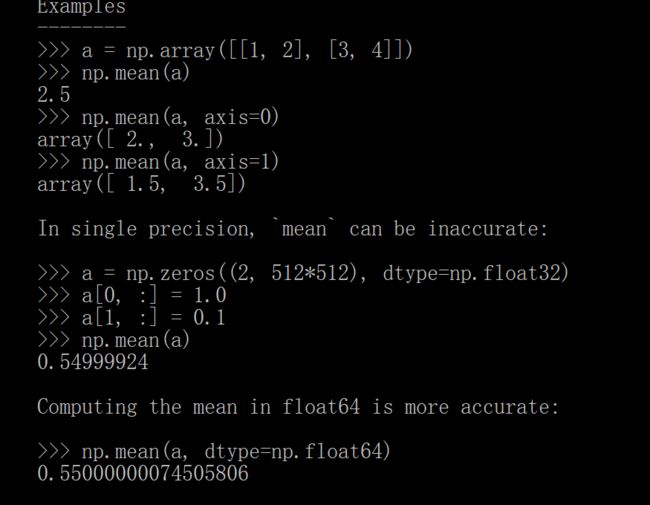
还有一个mean函数，这个函数事求平均值的。

 

虽然可以输入很多参数，不过我们可能用不到这么多，aixs=0的时侯是计算列的平均值，axis=1的时候是计算行的平均值。

 

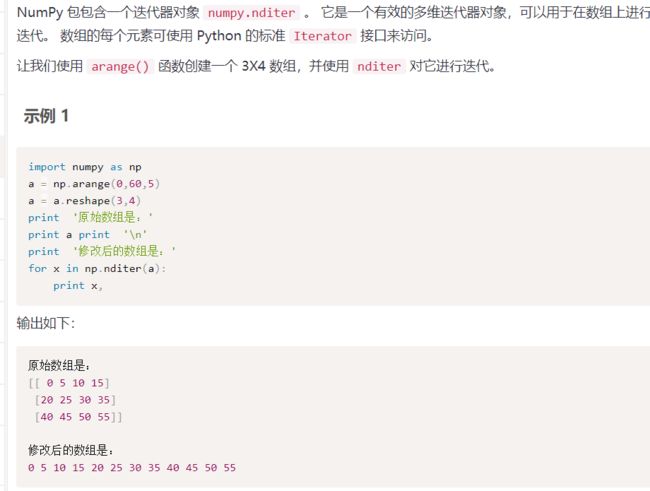
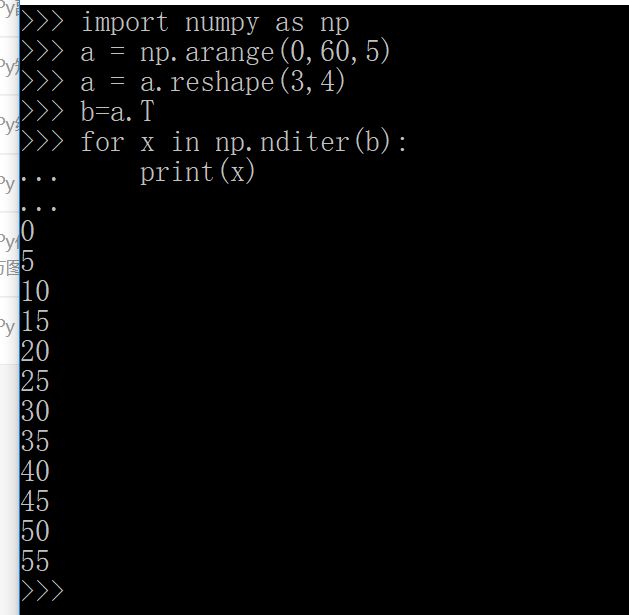
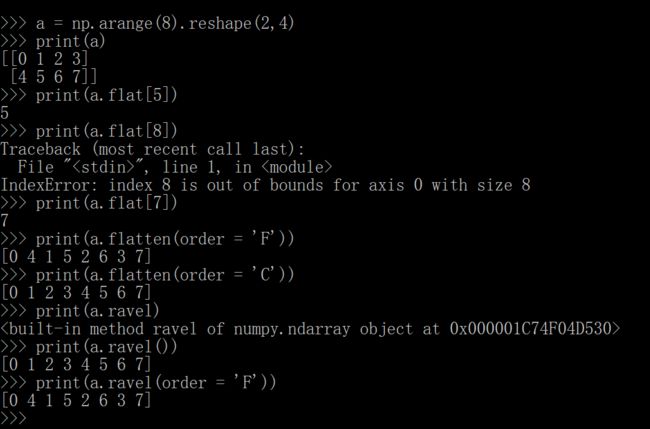
数组上的迭代

 

 

 

 

 

 

 

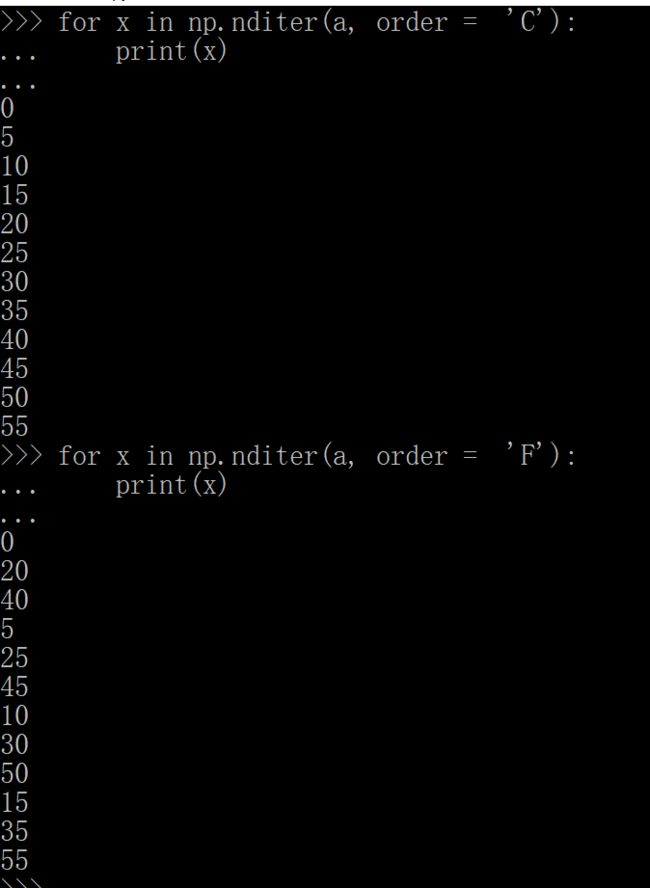
关于迭代顺序：

 

 

 

 

 

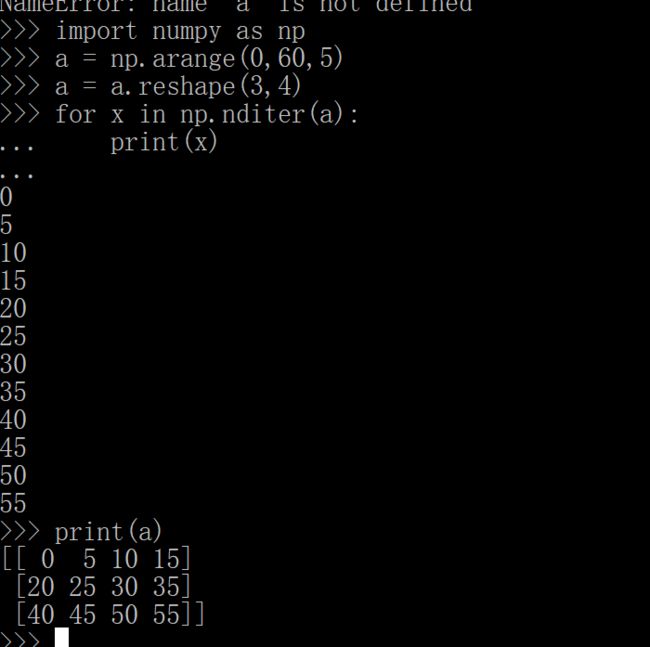
enmmm，按理说默认的order是C风格的，

 

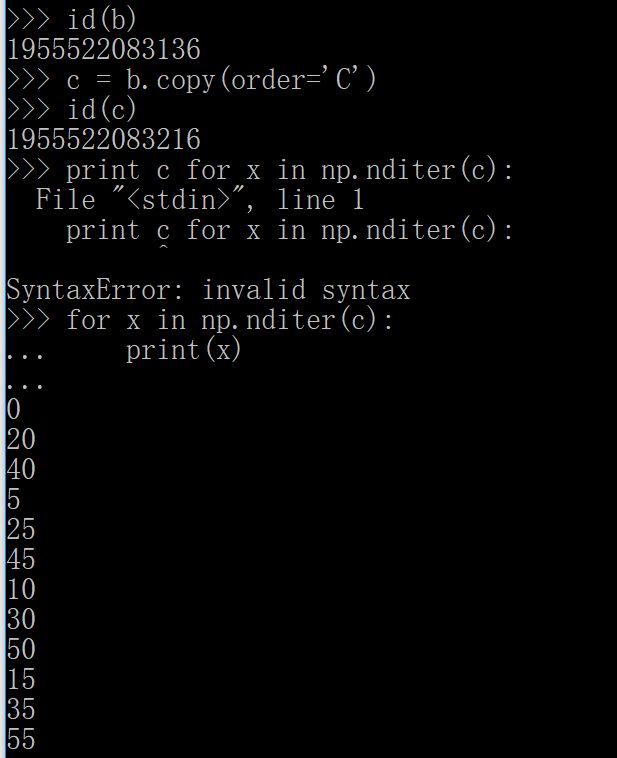
那么b和c都应该是C风格的，但是不知道为什么输出不一样。这里不作为重点吧，就看看吧。

 

 

 

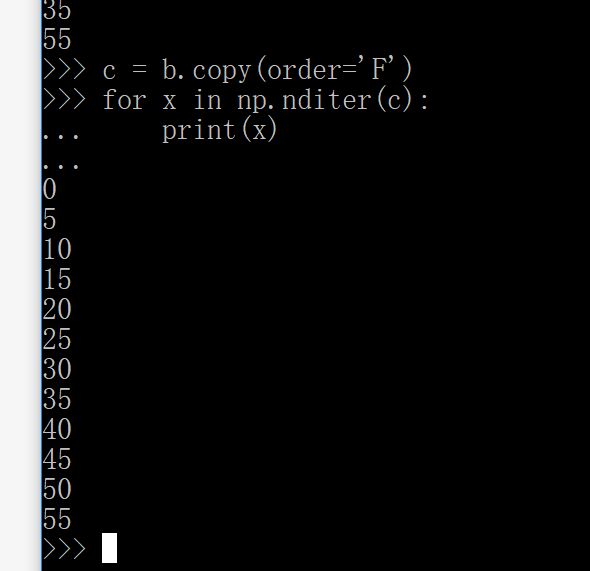
前面也介绍过，C和F一个是按照行存储，一个是存储，打印出来应该是按照这个顺序的，但是这个解释不了b=a.T输出为什么不变，可能是因为T一下，C风格也变成F风格了。

 

 

 

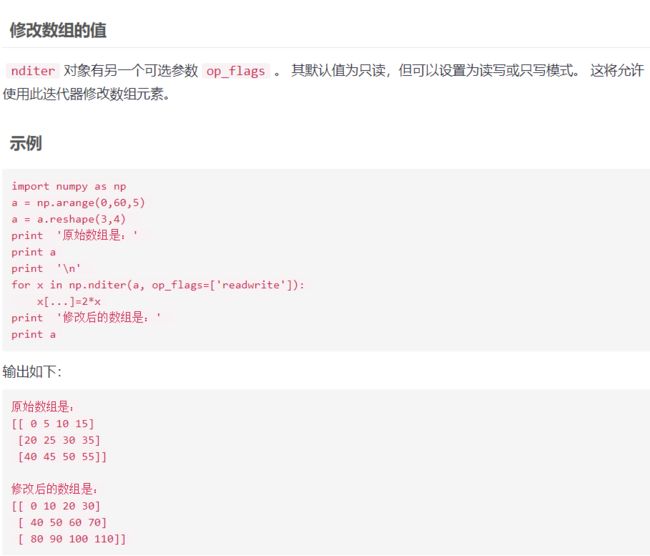
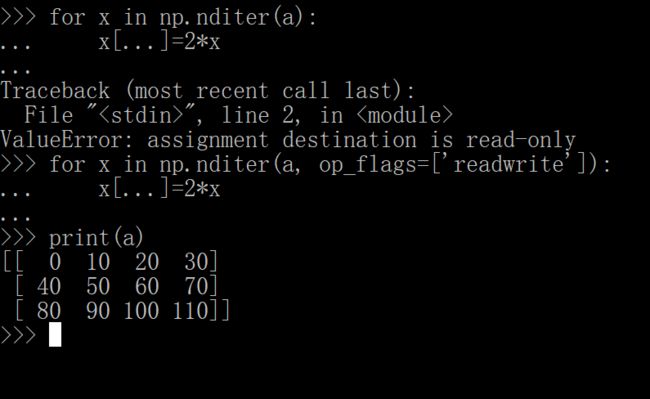
可以明显看出来确实是改变，不过这个似乎没什么用，我们直接a=a*2也可以得到相同的效果。

 

 

 

 

 

enmm这块也没什么问题吧，继续往下：

数组操作

 

这个我们还是比较熟悉的，只不过我们是直接用的a.shape这种格式，这有点像python类的实例化对象调用函数，这两种格式都可以。

 

 

 

 

 

 

 

这个没什么难理解的地方。

 

 

 

 

 

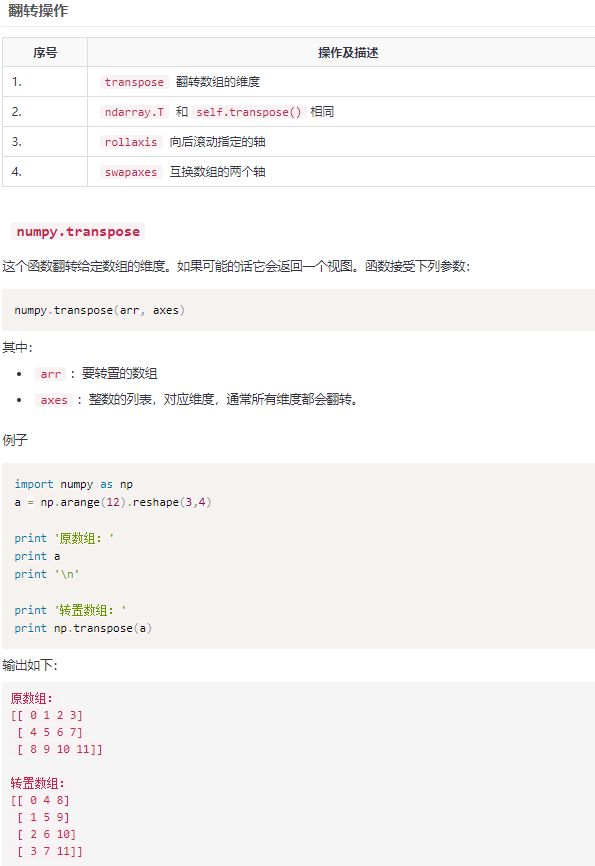
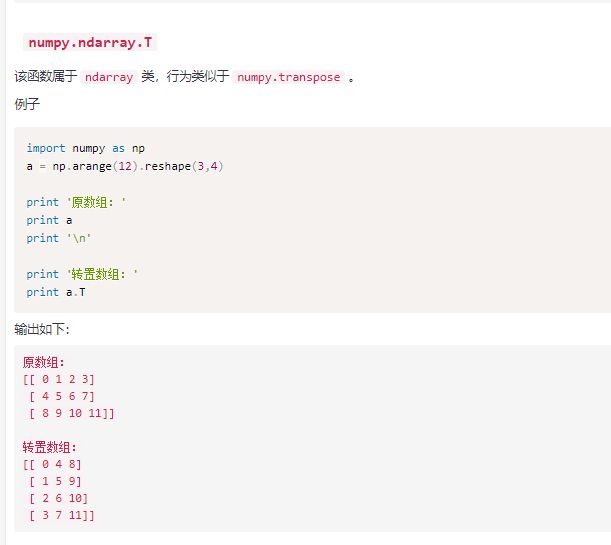
转置的两种方法吧，T再MATLAB里面也有转置，还有'也是转置的意思。不过复数有点特殊，分为共轭转置和转置，

 

conj就是求共轭的。

 

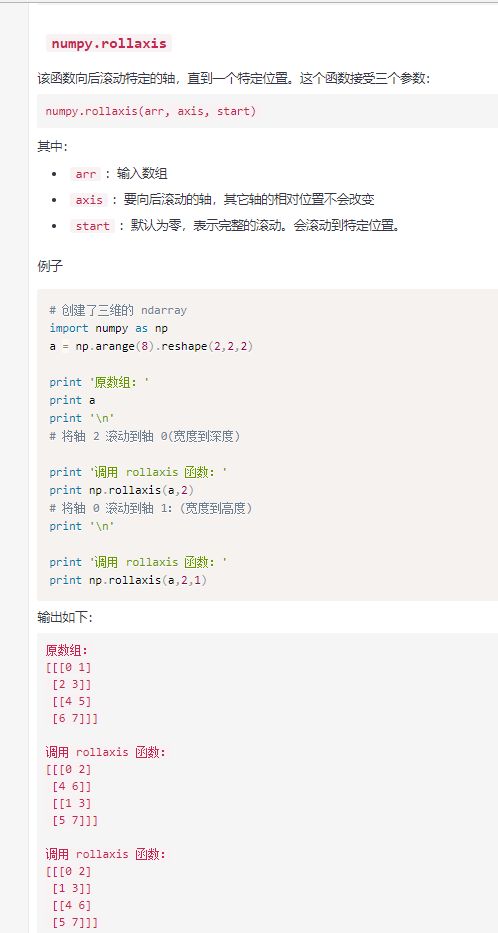
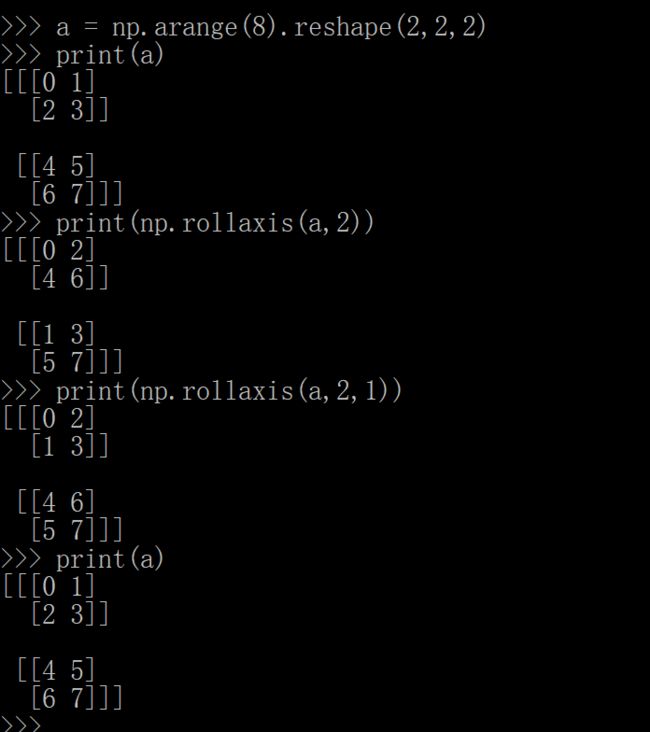
0,1,2轴的顺序就是从最层的中括号开始的，最外面是0轴，依次向里增加。

 

这个是不会影响原来的数组的。(a,2,1)应该是从2转到1，上面写错了。

 

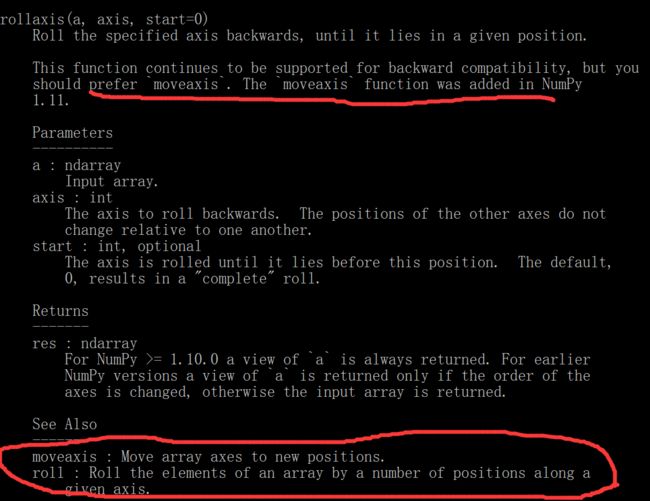
但是这个怎么转的我还是比较蒙，轴2转到轴1好理解，但是。我help了一下。

 

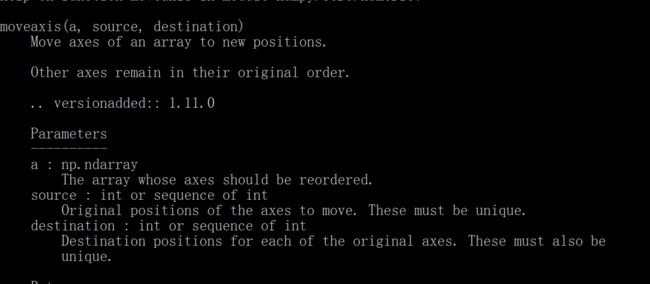
官方给出的建议是用moveaxis函数。这个其它的轴的位置是不会变的。

 

 

 

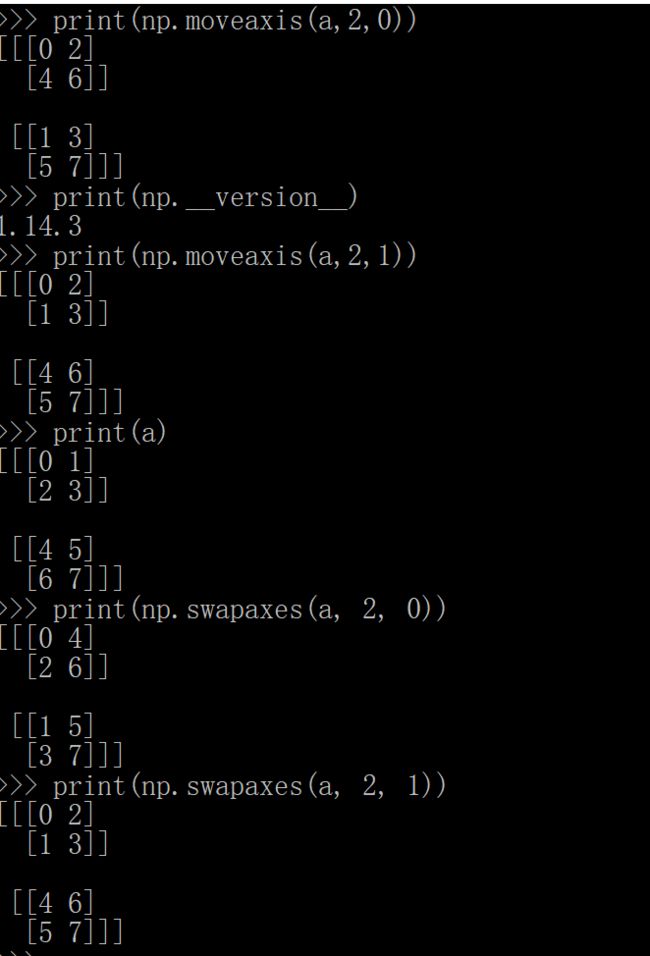
这个函数看来还没有加到np.ndarray类的方法里面去，不过我还是看不懂（2，0）为什么要这么转，为什么1轴要动呢？到实用的时候我们再看看。

 

 

 

这个1轴确实是没有动，这个是比较好理解的。

 

 

 

感觉这个有点没用啊。

 

 

 

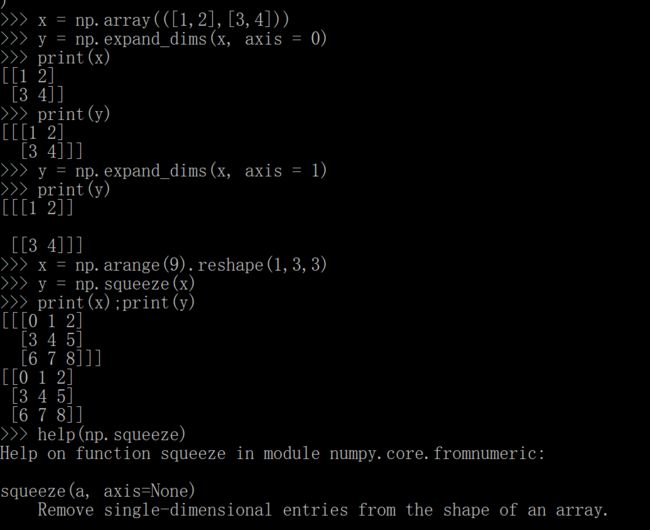
这里的符合广播规则其实就是说，必须在shape补全之后有一个维度的值是1才可以。

 

 

 

 

 

 

 

 

 

 

 

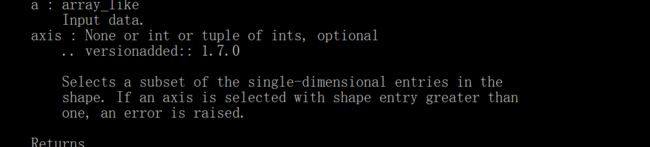
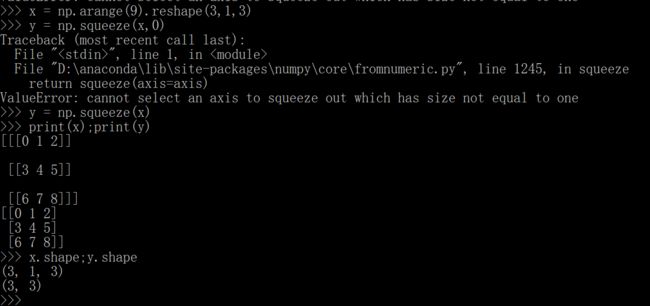
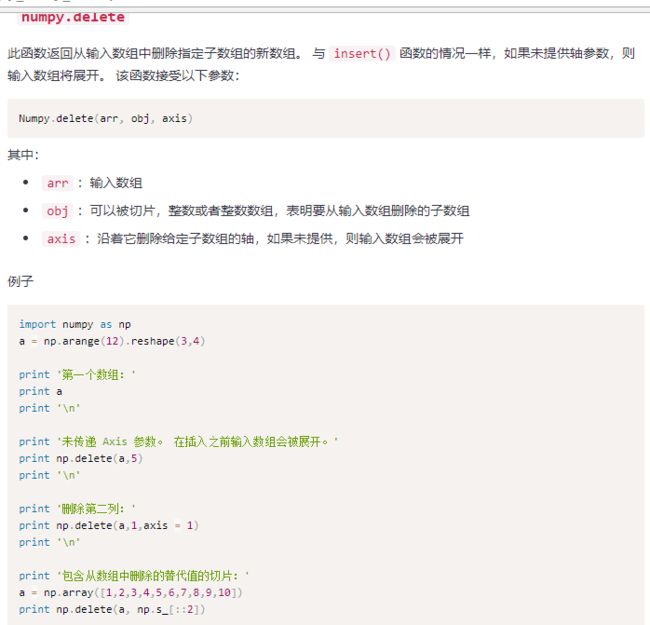
这个删除某一个维度的前提是那个维度上的值为1，不是1就会报错，如果不指定轴的话，就是会把维度对应的值为1的维度删掉，如果没有维度为1的，则数组不变。

 

 

 

 

 

这两个功能一样，值得提醒的是，这里没有广播机制，数组的形状必须完全一样才可以。

 

说到完全一样，有一个地方需要注意，这个地方是不补全shape的，也就是说(1,4)和(4,)是不一样的，其实打印出来看一看就知道，或者一看其实就知道一个是一维数组，一个是二维数组（维数就看中括号的对数吗，我觉得我们还是不要拿矩阵的角度来看numpy的数组，还是就看做n维数组吧），明显不一样，只有在广播体系中，它们才被看做一样，因为广播的时候会补全。   

 

 

 

 

 

 

 

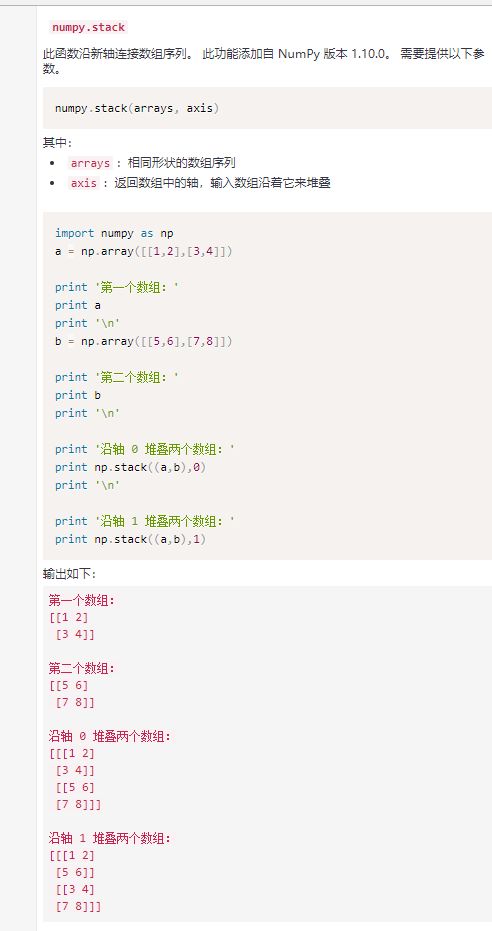
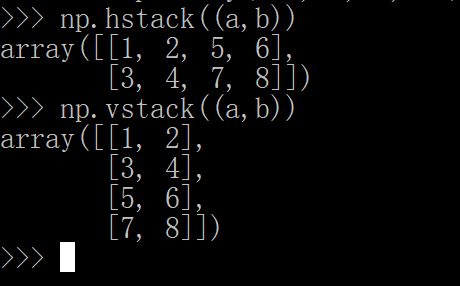
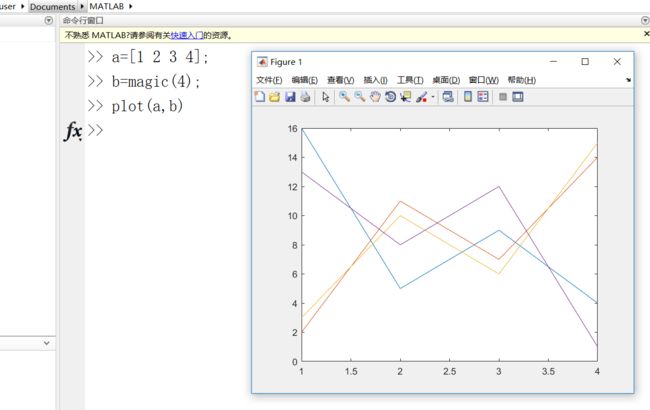
这两个其实上面用stack就可以实现。在这里我要对比一下MATLAB里面的矩阵连接，比较简单一些。看一个例子：

 

空格或者逗号事横着拼接，分号是竖着拼接。不过矩阵，其实一维的我们更习惯叫向量，矩阵或者向量的形状肯定是要一样的。MATLAB里面有没有广播机制呢？其实也有，在plot(x,y)的时候，如果x是一个(1,4)的，而y是一个(4,4)的，那么就会画出来四条曲线，这个也算一种广播吧。

 

 

 

 

 

 

 

 

 

 

 

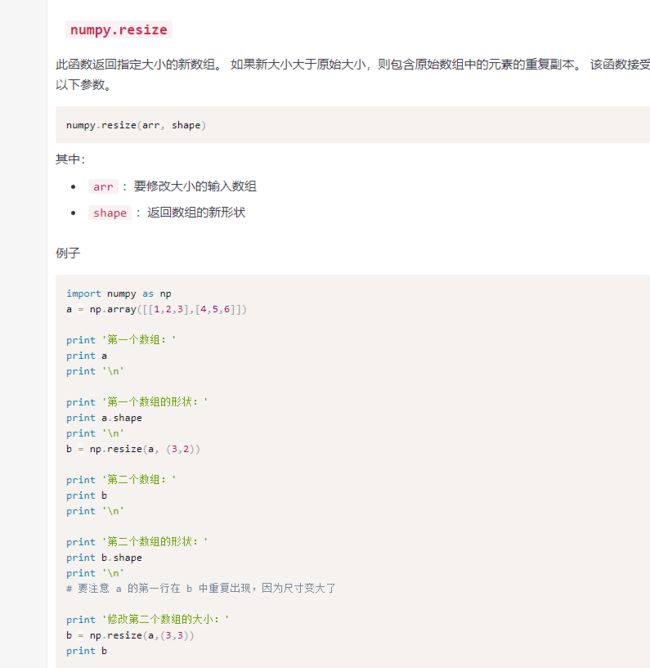
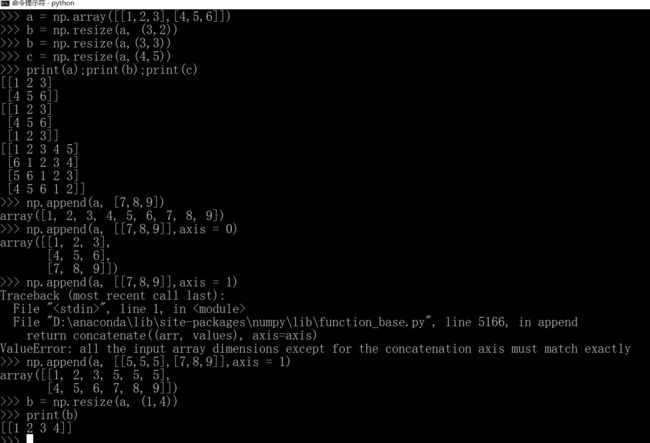
resize和reshape的区别在上面也可以看到，就是resize可以缺少或者补充元素，但是reshape不可以。append如果不输入轴，会被展开，生成一个flatten的格式的数组。

 

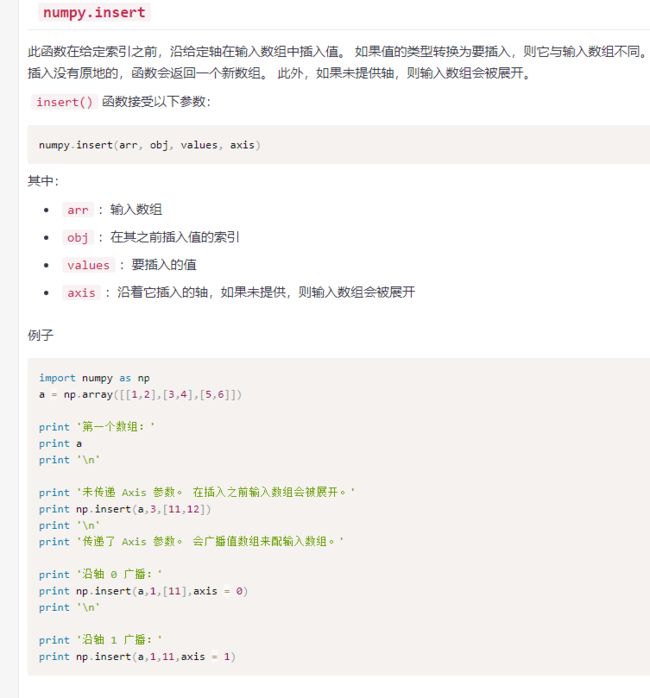
insert是有广播体系的。

 

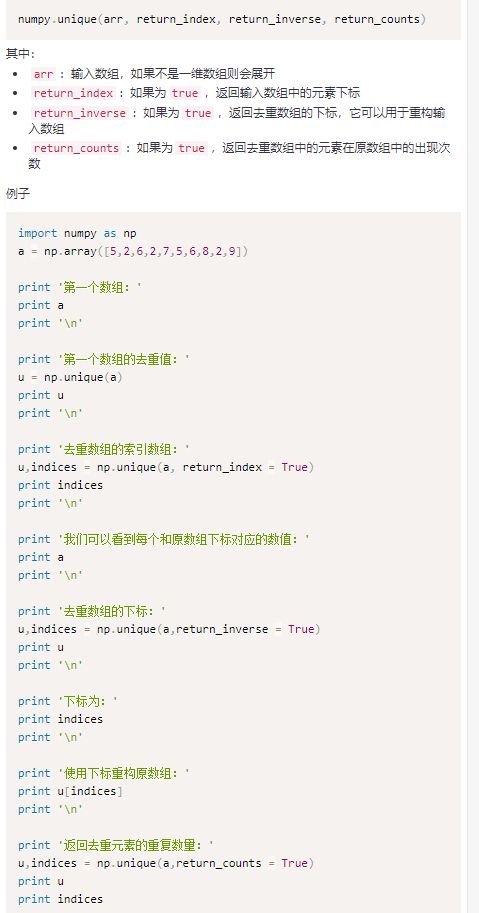
numpy.unique

此函数返回输入数组中的去重元素数组。 该函数能够返回一个元组，包含去重数组和相关索引的数组。 索引的性质取决于函数调用中返回参数的类型。

 

 

 

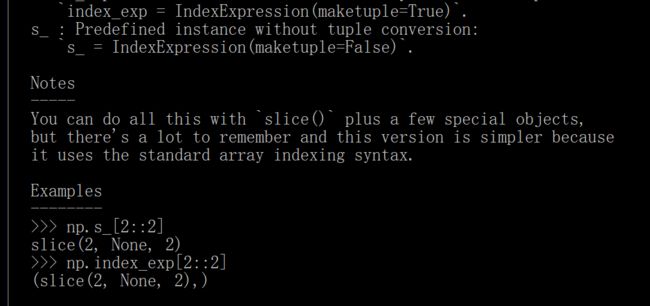
s_就类似一个切片操作。s_[::2]就是步长为2。

 

unique在MATLAB里面也是有的，在linux里面其实也是有的。

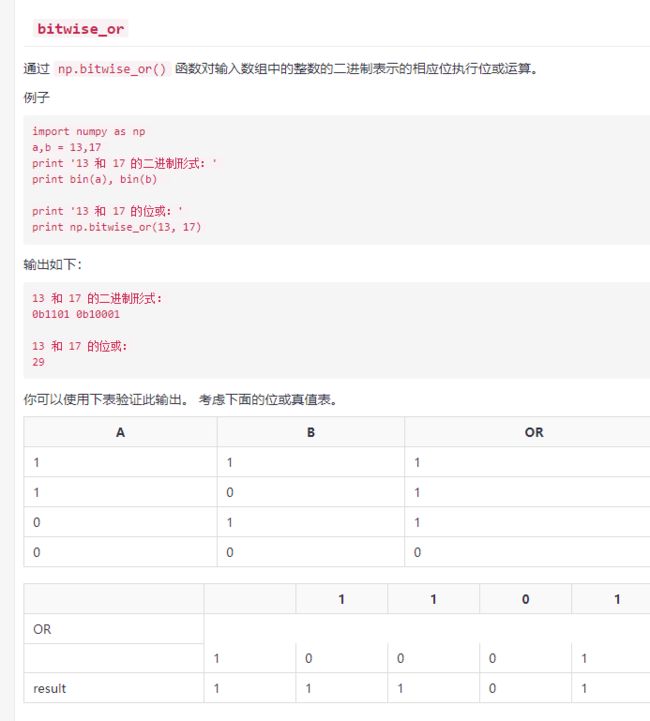
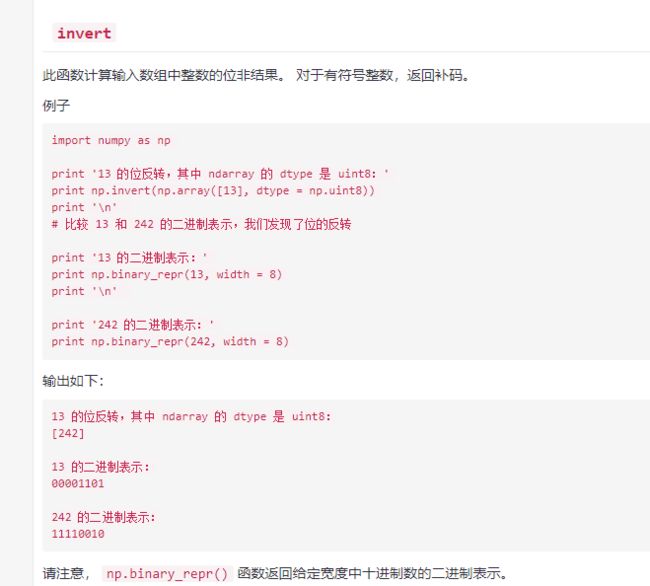
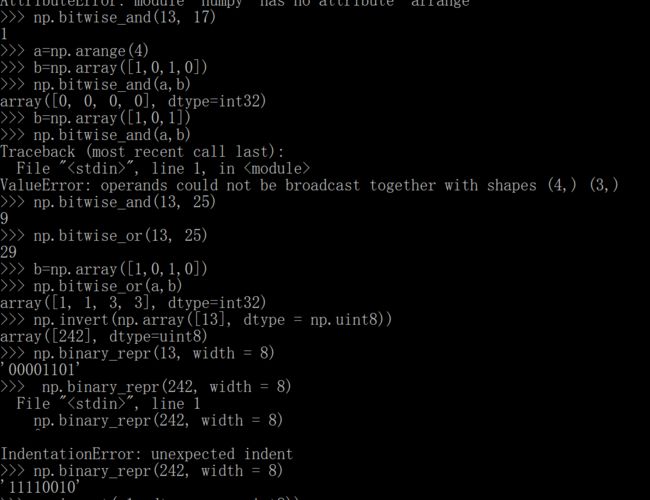
位操作

 

 

 

 

 

 

 

 

 

 

 

 

 

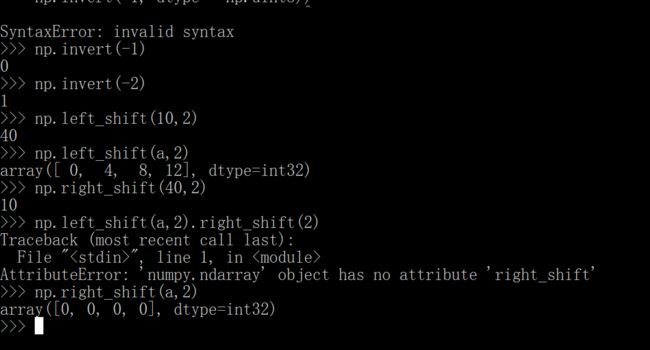
-1的原码是10000001，补码是11111111，那么按位取反就是00000000就是0，-2的原码是10000010，补码是11111110，再按位取反就是00000001，就是1。

这一讲内容挺杂的。