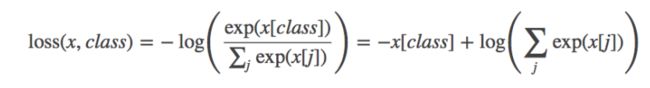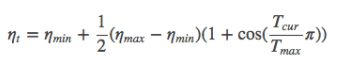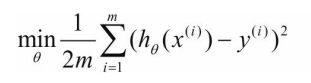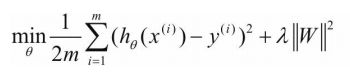pytorch深度学习和入门实战（四）神经网络的构建和训练

前言

1.前言

构建神经网络的话，应该对于深度学习有个基本的了解，知道什么是卷积、步幅、dropout、batch_size等，了解一下基本DNN/CNN/.RNN网络基本结构， 认知一下CV/NLP等方向基本内容等等。如果可以的话，最好去看一下吴恩达的视频（入门技巧，相关视频），有一个初步的入门。
如果时间紧张的话，那可以参见一下我前面总结的深度学习概览
深度学习知识梳理（干货满满详解DNN/CNN/RNN）之神经网络基础（一）
深度学习知识梳理（干货满满详解DNN/CNN/RNN）之深度学习网络结构（二）
深度学习知识梳理（干货满满详解DNN/CNN/RNN）之深度学习网络模型（三）
深度学习知识梳理（干货满满详解DNN/CNN/RNN）之模型训练（四）
深度学习知识梳理（干货满满详解DNN/CNN/RNN）之评估与调参（五）

神经网络概述

2.神经网络概述

神经网络看起来很复杂，节点很多，层数多，参数更多。但核心部分或组件不多，把这些组件确定后，这个神经网络基本就确定了。

2.1 核心组件包括：

1）层：神经网络的基本结构，将输入张量转换为输出张量。
2）模型：层构成的网络。
3）损失函数：参数学习的目标函数，通过最小化损失函数来学习各种参数。
4）优化器：如何使损失函数最小，这就涉及优化器。

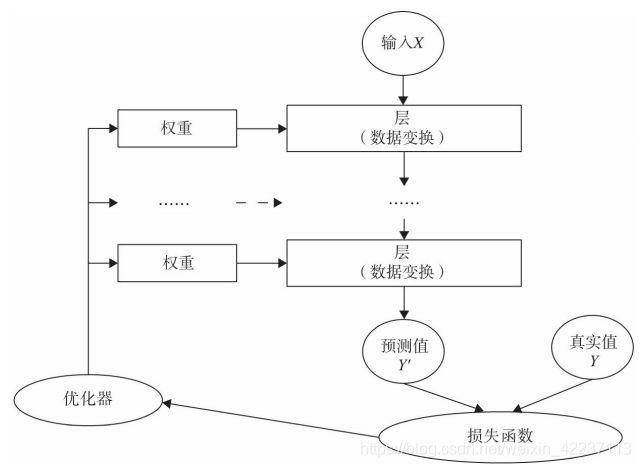
当然这些核心组件不是独立的，它们之间，以及它们与神经网络其他组件之间有密切关系。为便于理解，我们可以把这些关键组件及相互关系，用下图表示

说明：
多个层链接在一起构成一个模型或网络，

输入数据通过这个模型转换为预测值，然后损失函数把预测值与真实值进行比较，得到损失值（损失值可以是距离、概率值等），该损失值用于衡量预测值与目标结果的匹配或相似程度，

优化器利用损失值更新权重参数，从而使损失值越来越小。

这是一个循环过程，当损失值达到一个阀值或循环次数到达指定次数，循环结束。

伪代码表示：
Target ：

minimize  loss  <--- (loss / accuracy requirement  or certain  numbers of iterations)

Methods：

loop if not meet loss requirement:
	ouput <---  model(input)
	loss <---  loss_funtion(output , ground_truth)
	optimizer(loss) <--- Wi - Lr* d(loss)/d(Wi)

Result：

	reduce model losss,  improve accuracy and robost

2.2 核心过程

前向传播的过程:
数据的输入（input）➩ 定义的模型(model) ➩ 预测输出(output)

反向传播过程：
将ground truth和预测输出output, 送入损失函数function，计算loss。
最后通过优化器optimizer, 利用链式法则进行权重的反向更新（反向传播过程Back Propagation）。

说明:
在了解了pytorch神经网络组件基本模块和模型构成方法后，大致可以搭建出来forward的过程（有一个网络模型结构）。

但是， 你是否也有以下疑问：
对于不同的问题，是否有什么网络层是能帮助模型快速收敛或者提升精度的？
采用什么样的损失函数计算loss？
不同情况采用什么optimizer函数能提高优化检测效果和准确度？
相关的学习率是否可以在训练过程有计划性改变？
反向传播过程是否能自动执行、有没有必要清除gradent？等等

所以，带着如是问题，
我们下面将进一步了解一下如何搭建神经网络模型 ;
以及s在前向传播、反向传播过程中模型的参数设置、
模型各种层的提高模型精度和收敛性的trick和通用函数选择、
分布式训练过程等。

神经网络模型构建

3.构建神经网络模型

使用PyTorch构建神经网络使用的主要工具（或类）及相互关系,如下图所示：

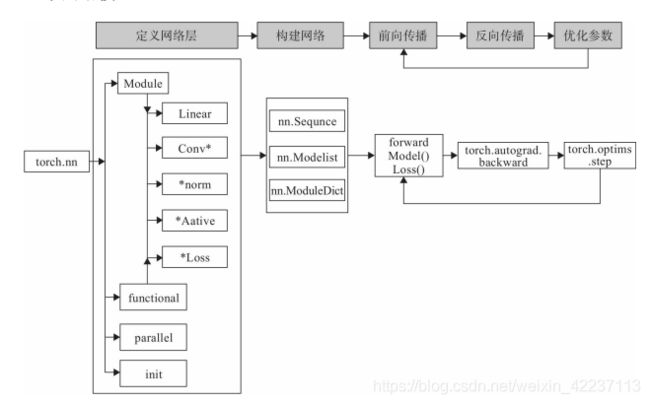
3.1构建网络层（Layer ➨ Model）

首先，定义类的时候，必须继承 nn.Module 这个父类，要让 PyTorch 知道这个类是一个 Module。

其次，在__init__(self)中设置好需要的“组件"(如 conv、pooling、Linear、BatchNorm等)。

最后，在 forward(self, x)中用定义好的“组件”进行组装，就像搭积木，把网络结构搭建出来，这样一个模型就定义好了

特别说明：
构建网络层可以基于Module类或函数（nn.functional）。nn中的大多数层（Layer）在functional中都有与之对应的函数。nn.functional中函数与nn.Module中的Layer的主要区别是后者继承Module类，会自动提取可学习的参数。而nn.functional更像是纯函数。两者功能相同，且性能也没有很大区别，那么如何选择呢？
像卷积层、全连接层、Dropout层等因含有可学习参数，一般使用继承nn.Module，使用其中的子类进行表示；
而激活函数、池化层不含可学习参数，可以使用nn.functional中对应的函数表示。

下面举例说明：

import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):
    def __init__(self):
    #初始化网络架构
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.pool1 = nn.MaxPool2d(2, 2)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.pool2 = nn.MaxPool2d(2, 2)
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    # 前向传播
    def forward(self, x):
        x = self.pool1(F.relu(self.conv1(x)))
        x = self.pool2(F.relu(self.conv2(x)))
        x = x.view(-1, 16 * 5 * 5)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    # 定义权值初始化
    def initialize_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                torch.nn.init.xavier_normal_(m.weight.data)
                if m.bias is not None:
                    m.bias.data.zero_()
            elif isinstance(m, nn.BatchNorm2d):
                m.weight.data.fill_(1)
                m.bias.data.zero_()
            elif isinstance(m, nn.Linear):
                torch.nn.init.normal_(m.weight.data, 0, 0.01)
                m.bias.data.zero_()

代码说明：

（1）第一行是初始化，往后定义了一系列组件，如由 Conv2d 构成的 conv1，有 MaxPool2d
构成的 poo1l，这些操作均由 torch.nn 提供，torch.nn 中的操作可查看文档：
https://PyTorch.org/docs/stable/nn.html#。

（2）定义好每层后，最后还需要通过前向传播的方式把这些串起来。这就是涉及如何定义forward函数的问题。forward函数的任务需要把输入层、网络层、输出层链接起来，实现信息的前向传导。该函数的参数一般为输入数据，返回值为输出数据。

x 为模型的输入，第一行表示，x 经过 conv1，然后经过激活函数 relu，再经过 pool1 操作；
第二行于第一行一样；第三行，表示将 x 进行 reshape，为了后面做为全连接层的输入；
第四，第五行的操作都一样，先经过全连接层 fc，然后经过 relu；
第六行，模型的最终输出是 fc3 输出。

（3）至此，一个模型定义完毕，接着就可以在后面进行使用。
例如，实例化一个模型 net = Net()，然后把输入 inputs 扔进去，outputs = net(inputs)，就可
以得到输出 outputs。

3.2 torch.nn.Sequential的3大使用方法

类似于keras中的序贯模型，当一个模型较简单的时候，我们可以使用torch.nn.Sequential类来实现简单的顺序连接模型。这个模型也是继承自torch.nn.Module类的。

常用3种使用方法：

(1) 最简单的序贯模型

import torch.nn as nn
model = nn.Sequential(
                  nn.Conv2d(1,20,5),
                  nn.ReLU(),
                  nn.Conv2d(20,64,5),
                  nn.ReLU()
                )
 
print(model)
print(model[2]) # 通过索引获取第几个层

'''运行结果为：
Sequential(
  (0): Conv2d(1, 20, kernel_size=(5, 5), stride=(1, 1))
  (1): ReLU()
  (2): Conv2d(20, 64, kernel_size=(5, 5), stride=(1, 1))
  (3): ReLU()
)
Conv2d(20, 64, kernel_size=(5, 5), stride=(1, 1))
'''

注意：

这样做有一个问题，每一个层是没有名称，默认的是以0、1、2、3来命名，从上面的运行结果也可以看出.

(2) 给每一个层添加名称

import torch.nn as nn
from collections import OrderedDict

model = nn.Sequential(OrderedDict([
                  ('conv1', nn.Conv2d(1,20,5)),
                  ('relu1', nn.ReLU()),
                  ('conv2', nn.Conv2d(20,64,5)),
                  ('relu2', nn.ReLU())
                ]))
 
print(model)
print(model[2]) # 通过索引获取第几个层

'''运行结果为：
Sequential(
  (conv1): Conv2d(1, 20, kernel_size=(5, 5), stride=(1, 1))
  (relu1): ReLU()
  (conv2): Conv2d(20, 64, kernel_size=(5, 5), stride=(1, 1))
  (relu2): ReLU()
)
Conv2d(20, 64, kernel_size=(5, 5), stride=(1, 1))
'''

注意：

从上面的结果中可以看出，这个时候每一个层都有了自己的名称，但是此时需要注意，我并不能够通过名称直接获取层，依然只能通过索引index，即
model[2] 是正确的
model[“conv2”] 是错误的
这其实是由它的定义实现的，看上面的Sequenrial定义可知，只支持index访问。

(3) Sequential的第三种实现

import torch.nn as nn
from collections import OrderedDict
model = nn.Sequential()
model.add_module("conv1",nn.Conv2d(1,20,5))
model.add_module('relu1', nn.ReLU())
model.add_module('conv2', nn.Conv2d(20,64,5))
model.add_module('relu2', nn.ReLU())
 
print(model)
print(model[2]) # 通过索引获取第几个层

熟悉keras的小伙伴在这里一定特别熟悉，这不就是keras的做法嘛，的确是的，但是Sequential里面好像并没有这么定义add_module()方法啊，
实际上，这个方法是定义在它的父类Module里面的，Sequential继承了而已，它的定义如下：

def add_module(self, name, module):

总结：

上面的3种定义顺序模型的方法是较为常见的，但是我们说了Sequential除了本身可以用来定义模型之外，它还可以包装层，把几个层包装起来像一个块一样。参见（4）

(4) 举一个复杂的例子：Resnet34
这部分代码从 github：
https://github.com/yuanlairuci110/PyTorch-best-practice-master/blob/master/models/ResNet34.py上获取.

class ResidualBlock(nn.Module):
 '''
 实现子 module: Residual Block
 '''
 def __init__(self, inchannel, outchannel, stride=1, shortcut=None):
 	super(ResidualBlock, self).__init__()
 	self.left = nn.Sequential(
 		nn.Conv2d(inchannel, outchannel, 3, stride, 1, bias=False),
 		nn.BatchNorm2d(outchannel),
		nn.ReLU(inplace=True),
 		nn.Conv2d(outchannel, outchannel, 3, 1, 1, bias=False),
 		nn.BatchNorm2d(outchannel))
 	self.right = shortcut
 def forward(self, x):
 	out = self.left(x)
 	residual = x if self.right is None else self.right(x)
 	out += residual
 return F.relu(out)

class ResNet34(BasicModule):
 '''
 实现主 module：ResNet34
 ResNet34 包含多个 layer，每个 layer 又包含多个 Residual block
 用子 module 来实现 Residual block，用_make_layer 函数来实现 layer
 '''
 def __init__(self, num_classes=2):
 	super(ResNet34, self).__init__()
 	self.model_name = 'resnet34'
 	# 前几层: 图像转换
 	self.pre = nn.Sequential(
 		nn.Conv2d(3, 64, 7, 2, 3, bias=False),
 		nn.BatchNorm2d(64),
 		nn.ReLU(inplace=True),
 		nn.MaxPool2d(3, 2, 1))
 	# 重复的 layer，分别有 3，4，6，3 个 residual block
 	self.layer1 = self._make_layer(64, 128, 3)
 	self.layer2 = self._make_layer(128, 256, 4, stride=2)
 	self.layer3 = self._make_layer(256, 512, 6, stride=2)
 	self.layer4 = self._make_layer(512, 512, 3, stride=2)

 	# 分类用的全连接
 	self.fc = nn.Linear(512, num_classes)
 def _make_layer(self, inchannel, outchannel, block_num, stride=1):
 '''
 构建 layer,包含多个 residual block
 '''
 	shortcut = nn.Sequential(
 		nn.Conv2d(inchannel, outchannel, 1, stride, bias=False),
 		nn.BatchNorm2d(outchannel))
 	layers = []
 	layers.append(ResidualBlock(inchannel, outchannel, stride, shortcut))
 	for i in range(1, block_num):
 		layers.append(ResidualBlock(outchannel, outchannel))
 	return nn.Sequential(*layers)
 def forward(self, x):
 	x = self.pre(x)
 	x = self.layer1(x)
 	x = self.layer2(x)
 	x = self.layer3(x)
 	x = self.layer4(x)
 	x = F.avg_pool2d(x, 7)
 	x = x.view(x.size(0), -1)
 	return self.fc(x)

代码说明:
还是从三要素出发看看是怎么定义 Resnet34 的：
首先，继承 nn.Module；
其次，看__init__()函数，在__init__()中，定义了这些组件，self.pre，self.layer1-4,
self.fc ；
最后，看 forward()，分别用了在__init__()中定义的一系列组件，并且用了
torch.nn.functional.avg_pool2d 这个操作

另外，torch.nn.Sequential 其实就是 Sequential 容器，该容器将一系列操作按先后顺序给包起来，并且将多个layer包装成block，方便重复使用。

至此，网络构建部分完成

3.3.神经网络模型构建总结

模型的定义就是先继承，再构建组件，最后组装。
像卷积层、全连接层、Dropout层等因含有可学习参数，一般使用继承nn.Module，使用其中的子类进行表示；
而激活函数、池化层不含可学习参数，可以使用nn.functional中对应的函数表示.
同时为了方便重复使用组件，可以使用 Sequential 容器将一系列组件包起来，最后在 forward()函数中将这些组件组装成你的模型

损失函数和优化器

我们准备好数据，设计好模型，接下来就是选择合适的损失函数，并且采用合适的优化器进行优化(训练)模型。

4. pytorch中18种损失函数

4.1 概述

损失函数（Loss Function）在机器学习中非常重要，因为训练模型的过程实际就是优化损失函数的过程。

损失函数对每个参数的偏导数就是梯度下降中提到的梯度，防止过拟合时添加的正则化项也是加在损失函数后面。
损失函数用来衡量模型的好坏，损失函数越小说明模型和参数越符合训练样本。
任何能够衡量模型预测值与真实值之间的差异的函数都可以叫作损失函数。

在机器学习中常用的损失函数有两种，即交叉熵(Cross Entropy)和均方误差（Mean squared error，MSE），分别对应机器学习中的分类问题和回归问题。

具体举例来说，对分类问题的损失函数一般采用交叉熵，交叉熵反应的两个概率分布的距离（不是欧氏距离）。分类问题进一步又可分为多目标分类，如一次要判断100张图是否包含10种动物，或单目标分类。
回归问题预测的不是类别，而是一个任意实数。在神经网络中一般只有一个输出节点，该输出值就是预测值。反应的预测值与实际值之间的距离可以用欧氏距离来表示，所以对这类问题通常使用均方差作为损失函数。

4.2 损失函数类表

针对不同的问题，可以直接调用现有的损失函数。18种损失函数如下：

类	算法名称	适用场景	说明
torch.nn.L1Loss()	平均绝对值误差损失	回归问题	计算 output 和 target 之差的绝对值，可选返回同维度的 tensor 或者是一个标量。
torch.nn.MSELoss()	均方误差损失	回归	计算 output 和 target 之差的平方，可选返回同维度的 tensor 或者是一个标量。
torch.nn.CrossEntropyLoss()	交叉熵损失	多分类	将输入经过 softmax 激活函数之后，再计算其与 target 的交叉熵损失。即该方法将nn.LogSoftmax()和 nn.NLLLoss()进行了结合。
nn.CTCLoss（）	连接时序分类	时序分类问题	这个方法主要是解决神经网络label 和output 不对齐的问题，其优点是不用强制对齐标签且标签可变长，仅需输入序列和监督标签序列即可进行训练主要适用场景文本识别、语音识别/及手写字识别等工程场景
torch.nn.NLLLoss()	负对数似然函数损失	多分类	loss(input, class) = -input[class_index]
nn.PoissonNLLLoss（）	泊松损失	分类问题	用于 target 服从泊松分布的分类任务
torch.nn.KLDivLoss()	KL散度损失	回归	计算 input 和 target 之间的 KL 散度( Kullback–Leibler divergence)
torch.nn.BCELoss()	二分类交叉熵损失	二分类	二分类任务时的交叉熵计算函数。此函数可以认为是 nn.CrossEntropyLoss 函数的特例。其分类限定为二分类，y 必须是{0,1}。还需要注意的是，input 应该为概率分布的形式，这样才符合交叉熵的应用
torch.nn.BCEWithLogitsLoss（）	二分类交叉熵损失(output进行sigmoid概率化)	二分类问题	将 Sigmoid 与 BCELoss 结合，类似于 CrossEntropyLoss(将 nn.LogSoftmax()和 nn.NLLLoss()进行结合）。即 input 会经过 Sigmoid 激活函数，将 input 变成概率分布的形式。
torch.nn.MarginRanKingLoss()	评价相似度的损失	------	计算两个向量之间的相似度，当两个向量之间的距离大于 margin，则 loss 为正，小于margin，loss 为 0。
torch.nn.HingeEmbeddingLoss()	合页损失	通常用于学习非线性嵌入或半监督学习。	为折页损失的拓展，主要用于衡量两个输入是否相似
torch.nn.MultiLabelMarginLoss()	多标签分类的损失	多标签分类	用于一个样本属于多个类别时的分类任务
torch.nn.SmoothL1Loss()	平滑的L1损失	回归	计算平滑 L1 损失，属于 Huber Loss 中的一种
torch.nn.SoftMarginLoss()	多标签二分类问题的损失	多标签二分类	创建一个标准，优化输入张量xx和目标张量yy（包含1或-1）之间的两类分类逻辑损失
torch.nn.MultiLabelSoftMarginLoss	多标签二分类问题的损失	多标签二分类	SoftMarginLoss 多标签版本
torch.nn.CosineEmbeddingLoss()	embeding 方式之一	通常用于学习非线性嵌入或半监督学习	用 Cosine 函数来衡量两个输入是否相似
torch.nn.MultiMarginLoss（）	多分类合页损失	分类问题	计算多分类的折页损失
torch.nn.TripletMarginLoss()	三元损失	人脸分类问题	计算三元组损失，人脸验证中常用。

详细的api和参数内容，以官方api为准： Loss Functions

4.3 举例说明

基本使用，实例代码，以交叉熵为例说明：

类参数：

torch.nn.CrossEntropyLoss(weight: Optional[torch.Tensor] = None, size_average=None, ignore_index: int = -100, reduce=None, reduction: str = 'mean')

计算公式

参数说明：

• weight(Tensor)-为每个类别的loss设置权值，常用于类别不均衡问题。weight必须是float类型的tensor，其长度要与类别C一致，即每一个类别都要设置weight。
  带weight的公式如下：
  
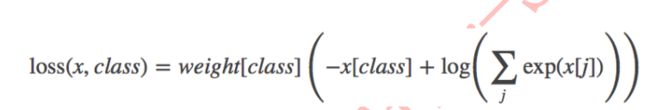
• size_average(bool)- 当 reduce=True 时有效。为 True 时，返回的 loss 为平均值；为 False
  时，返回的各样本的 loss 之和。
• reduce(bool)- 返回值是否为标量，默认为 True
• ignore_index(int)- 忽略某一类别，不计算其 loss，其 loss 会为 0，并且，在采用
  size_average 时，不会计算那一类的 loss，除的时候的分母也不会统计那一类的样本

Example1

import torch
import torch.nn as nn
torch.manual_seed(10)
loss = nn.CrossEntropyLoss()
#假设类别数为5
input = torch.randn(3, 5, requires_grad=True)
#每个样本对应的类别索引,其值范围为[0,4]
target = torch.empty(3, dtype=torch.long).random_(5)
output = loss(input, target)
output.backward()

Example2

# coding: utf-8

import torch
import torch.nn as nn
import numpy as np
import math

# ----------------------------------- CrossEntropy loss: base

loss_f = nn.CrossEntropyLoss(weight=None, size_average=True, reduce=False)
# 生成网络输出 以及 目标输出
output = torch.ones(2, 3, requires_grad=True) * 0.5      # 假设一个三分类任务，batchsize=2，假设每个神经元输出都为0.5
target = torch.from_numpy(np.array([0, 1])).type(torch.LongTensor)

loss = loss_f(output, target)

print('--------------------------------------------------- CrossEntropy loss: base')
print('loss: ', loss)
print('由于reduce=False，所以可以看到每一个样本的loss，输出为[1.0986, 1.0986]')


# 熟悉计算公式，手动计算第一个样本
output = output[0].detach().numpy()
output_1 = output[0]              # 第一个样本的输出值
target_1 = target[0].numpy()

# 第一项
x_class = output[target_1]
# 第二项
exp = math.e
sigma_exp_x = pow(exp, output[0]) + pow(exp, output[1]) + pow(exp, output[2])
log_sigma_exp_x = math.log(sigma_exp_x)
# 两项相加
loss_1 = -x_class + log_sigma_exp_x
print('---------------------------------------------------  手动计算')
print('第一个样本的loss：', loss_1)


# ----------------------------------- CrossEntropy loss: weight

weight = torch.from_numpy(np.array([0.6, 0.2, 0.2])).float()
loss_f = nn.CrossEntropyLoss(weight=weight, size_average=True, reduce=False)
output = torch.ones(2, 3, requires_grad=True) * 0.5  # 假设一个三分类任务，batchsize为2个，假设每个神经元输出都为0.5
target = torch.from_numpy(np.array([0, 1])).type(torch.LongTensor)
loss = loss_f(output, target)
print('\n\n--------------------------------------------------- CrossEntropy loss: weight')
print('loss: ', loss)  #
print('原始loss值为1.0986, 第一个样本是第0类，weight=0.6,所以输出为1.0986*0.6 =', 1.0986*0.6)

# ----------------------------------- CrossEntropy loss: ignore_index

loss_f_1 = nn.CrossEntropyLoss(weight=None, size_average=False, reduce=False, ignore_index=1)
loss_f_2 = nn.CrossEntropyLoss(weight=None, size_average=False, reduce=False, ignore_index=2)

output = torch.ones(3, 3, requires_grad=True) * 0.5  # 假设一个三分类任务，batchsize为2个，假设每个神经元输出都为0.5
target = torch.from_numpy(np.array([0, 1, 2])).type(torch.LongTensor)

loss_1 = loss_f_1(output, target)
loss_2 = loss_f_2(output, target)

print('\n\n--------------------------------------------------- CrossEntropy loss: ignore_index')
print('ignore_index = 1: ', loss_1)     # 类别为1的样本的loss为0
print('ignore_index = 2: ', loss_2)     # 类别为2的样本的loss为0

output:

--------------------------------------------------- CrossEntropy loss: base loss: tensor([1.0986, 1.0986], grad_fn=)
由于reduce=False，所以可以看到每一个样本的loss，输出为[1.0986, 1.0986]
--------------------------------------------------- 手动计算 第一个样本的loss： 1.0986122886681098

--------------------------------------------------- CrossEntropy loss: weight loss:
tensor([0.6592, 0.2197], grad_fn=)
原始loss值为1.0986, 第一个样本是第0类，weight=0.6,所以输出为1.0986*0.6 = 0.65916

--------------------------------------------------- CrossEntropy loss: ignore_index ignore_index = 1:tensor([1.0986, 0.0000, 1.0986],
grad_fn=) ignore_index = 2: tensor([1.0986, 1.0986, 0.0000], grad_fn=)

5. 优化器

5.1 optimizer基类及其方法

5.1.1 概述

优化器基类 Optimizer
PyTorch 中所有的优化器(如：optim.Adadelta、optim.SGD、optim.RMSprop 等)均是Optimizer 的子类，Optimizer 中定义了一些常用的方法，有 zero_grad()、step(closure)、state_dict()、load_state_dict(state_dict)和add_param_group(param_group)等。

5.1.2 API

class torch.optim.Optimizer(params, defaults)
Base class for all optimizers.

参数：

params (iterable) —— Variable 或者 dict的iterable。指定了什么参数应当被优化。
defaults —— (dict)：包含了优化选项默认值的字典（一个参数组没有指定的参数选项将会使用默值）。

optim包含的方法：
(1)add_param_group(param_group)

功能：给 optimizer 管理的参数组中增加一组参数，
可为该组参数定制 lr, momentum, weight_decay 等，在 finetune 中常用。
例如：optimizer_1.add_param_group({'params': w3, 'lr': 0.001, 'momentum': 0.8})

(2)load_state_dict(state_dict)

功能：将 state_dict 中的参数加载到当前网络，常用于 finetune

(3)state_dict()

功能：获取模型当前的参数，以一个有序字典形式返回。
这个有序字典中，key 是各层参数名，value 就是参数

(4)step(closure)

功能：执行一步权值更新, 其中可传入参数 closure（一个闭包）。如，当采用 LBFGS
优化方法时，需要多次计算，因此需要传入一个闭包去允许它们重新计算 loss

Example:

for input, target in dataset: 
	def closure(): 
		optimizer.zero_grad() 
		output = model(input) 
		loss = loss_fn(output, target) 
		loss.backward() 
		return loss 
	optimizer.step(closure)

(5)zero_grad()

功能：将梯度清零。由于 PyTorch 不会自动清零梯度，所以在每一次更新前会进行此操作。

5.2 pytorch的10大优化器

torch.optim.SGD
torch.optim.ASGD
torch.optim.Rprop
torch.optim.Adagrad
torch.optim.Adadelta
torch.optim.RMSprop
torch.optim.Adam(AMSGrad)
torch.optim.Adamax
torch.optim.SparseAdam
torch.optim.LBFGS

后续有时间可能需要单独开篇详解optim，暂时可参见：
官方api， 详见 https://pytorch.org/docs/stable/optim.html
PyTorch 学习笔记（七）：PyTorch的十个优化器

以下动态图，各个optim的性能可见一斑：
（1）收敛的可视化对比

（2）有鞍点收敛的对比

（3）收敛速度对比

5.3 优化器选择

优化算法有很多，如随机梯度下降法、自适应优化算法等，那么具体使用时该如何选择呢？
RMSprop、Adadelta和Adam被认为是自适应优化算法，因为它们会自动更新学习率。而使用SGD时，必须手动选择学习率和动量参数，通常会随着时间的推移而降低学习率。

有时可以考虑综合使用这些优化算法，如采用先使用Adam，然后使用SGD的优化方法，这个想法，实际上是由于在训练的早期阶段SGD对参数调整和初始化非常敏感。因此，我们可以通过先使用Adam优化算法来进行训练，这将大大地节省训练时间，且不必担心初始化和参数调整，一旦用Adam训练获得较好的参数后，就可以切换到SGD+动量优化，以达到最佳性能。

神经网络核心过程调优

6 前向传播（Forward Propagation）

定义好每层后，最后还需要通过前向传播的方式把这些串起来。这就是涉及如何定义forward函数的问题。forward函数的任务需要把输入层、网络层、输出层链接起来，实现信息的前向传导。该函数的参数一般为输入数据，返回值为输出数据。

在forward函数中，有些层来自nn.Module，也可以使用nn.functional定义。来自nn.Module的需要实例化（使用super(xxx_Net, self).__init__()继承，可以避免实例、直接使用），而使用nn.functional定义的可以直接使用。

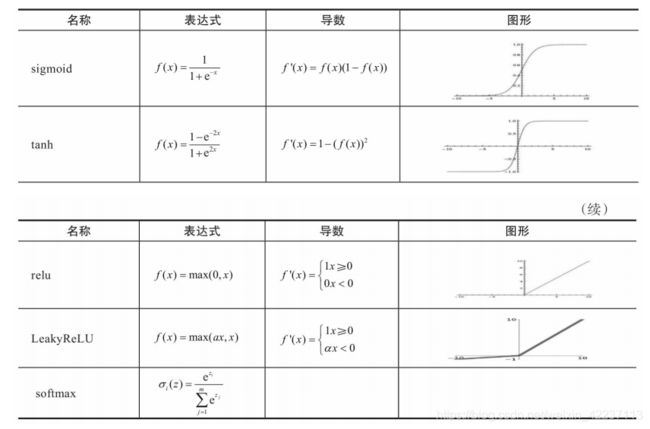
6.1 选择合适激活函数

激活函数在神经网络中作用有很多，主要作用是给神经网络提供非线性建模能力。如果没有激活函数，那么再多层的神经网络也只能处理线性可分问题。常用的激活函数有sigmoid、tanh、relu、softmax等。它们的图形、表达式、导数等信息如下图所示：

在搭建神经网络时，如何选择激活函数？

情况	选择激活函数	备注说明
如果搭建的神经网络层数不多	选择sigmoid、tanh、relu、softmax都可以	------
搭建比较深的神经网络时	relu类	此时一般不宜选择sigmoid、tanh激活函数，因它们的导数都小于1，尤其是sigmoid的导数在[0,1/4]之间，多层叠加后，根据微积分链式法则，随着层数增多，导数或偏导将指数级变小。所以层数较多的激活函数需要考虑其导数不宜小于1当然也不能大于1，小于1则容易梯度消失、大于1将导致梯度爆炸，导数为1最好，而激活函数relu正好满足这个条件。
多分类神经网络输出层	softmax	将输出转化为占比百分比，代表各类别的概率

6.2 权值初始化的十种方法

6.2.1 深度学习为何要初始化？

传统机器学习算法中很多并不是采用迭代式优化，因此需要初始化的内容不多。但深度学习的算法一般采用迭代方法，而且参数多、层数也多，所以很多算法不同程度上会受到初始化的影响。

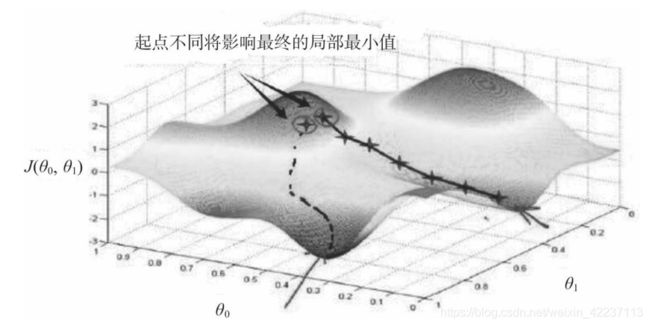
初始化对训练有哪些影响？初始化能决定算法是否收敛，如果算法的初始化不适当，初始值过大可能会在前向传播或反向传播中产生爆炸的值；如果太小将导致丢失信息。对收敛的算法适当的初始化能加快收敛速度。初始值的选择将影响模型收敛局部最小值还是全局最小值，如下图所示，因初始值的不同，导致收敛到不同的极值点。另外，初始化也可以影响模型的泛化.

6.2.2 如何对权重、偏移量进行初始化？初始化这些参数是否有一般性原则？

常见的参数初始化有零值初始化、随机初始化、均匀分布初始、正态分布初始和正交分布初始等。一般采用正态分布或均匀分布的初始值，实践表明 正态分布、正交分布、均匀分布的初始值能带来更好的效果。

继承nn.Module的模块参数都采取了较合理的初始化策略，一般情况使用其缺省初始化策略就足够了。

当然，如果想要修改，PyTorch也提供了nn.init模块，该模块提供了常用的初始化策略，如xavier、kaiming等经典初始化策略，使用这些初始化策略有利于激活值的分布呈现出更有广度或更贴近正态分布。

xavier一般用于激活函数是S型（如sigmoid、tanh）的权重初始化，而kaiming则更适合于激活函数为ReLU类的权重初始化.

6.2.2 api

PyTorch 在 torch.nn.init 中提供了常用的初始化方法函数，大致分为3大类：

1. Xavier 系列；
2. kaiming系列；
3. 其他方法分布

具体可以参见
Xavier 初始化方法，论文在《Understanding the difficulty of training deep feedforward neural networks》
官方api，参见https://pytorch.org/docs/stable/nn.init.html
PyTorch 学习笔记（四）：权值初始化的十种方法

6.2.3 举个栗子

参见本章中 3.2 ---->def initialize_weights(self)

6.3 Batch Normalization

参见 Batch Normalization基本原理详解

6.4 dropout正则化

参见 dropout基本原理详解

7 反向传播（Back Propagation）

前向传播函数定义好以后，接下来就是梯度的反向传播。这里关键是利用复合函数的链式法则。深度学习中涉及很多函数，如果要自己手工实现反向传播，比较费时。好在PyTorch提供了自动反向传播的功能，使用nn工具箱，无须我们自己编写反向传播，直接让损失函数（loss）调用backward()即可，非常方便和高效！

7.1 pytorch中六种学习率调整方法

具体用法，可以参见：
官网api

在模型训练的优化部分，调整最多的一个参数就是学习率，合理的学习率可以使优化器快速收敛。
一般在训练初期给予较大的学习率，随着训练的进行，学习率逐渐减小。学习率什么时候减小，减小多少，这就涉及到学习率调整方法。pytorch中提供了六种方法供大家使用，下面将一一介绍，最后对学习率调整方法进行总结。

7.1.1. lr_scheduler.StepLR

class torch.optim.lr_scheduler.StepLR(optimizer, 
									 step_size,
									 gamma=0.1, 
									 last_epoch=-1)

功能：

等间隔调整学习率，调整倍数为gamma倍，调整间隔为step_size。间隔单位是step。需要注意的是，step通常是指epoch，不要弄成iteration了。

参数：

step_size(int)- 学习率下降间隔数，若为30，则会在30、60、90…个step时，将学习率调整为lr*gamma。
gamma(float)- 学习率调整倍数，默认为0.1倍，即下降10倍。
last_epoch(int)- 上一个epoch数，这个变量用来指示学习率是否需要调整。当last_epoch符合设定的间隔时，就会对学习率进行调整。当为-1时，学习率设置为初始值。

7.1.2. lr_scheduler.MultiStepLR

class torch.optim.lr_scheduler.MultiStepLR(optimizer, 
										milestones, 
										gamma=0.1, 
										last_epoch=-1)

功能：

按设定的间隔调整学习率。这个方法适合后期调试使用，观察loss曲线，为每个实验定制学习率调整时机。

参数：

milestones(list)- 一个list，每一个元素代表何时调整学习率，list元素必须是递增的。如 milestones=[30,80,120]
gamma(float)- 学习率调整倍数，默认为0.1倍，即下降10倍。
last_epoch(int)- 上一个epoch数，这个变量用来指示学习率是否需要调整。当last_epoch符合设定的间隔时，就会对学习率进行调整。当为-1时，学习率设置为初始值。

7.1.3. lr_scheduler.ExponentialLR

class torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma, last_epoch=-1)

功能：

按指数衰减调整学习率，调整公式: lr = lr * gammaepoch

参数：

gamma- 学习率调整倍数的底，指数为epoch，即 gammaepoch
last_epoch(int)- 上一个epoch数，这个变量用来指示学习率是否需要调整。当last_epoch符合设定的间隔时，就会对学习率进行调整。当为-1时，学习率设置为初始值。

7.1.4.lr_scheduler.CosineAnnealingLR

class torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, 
												T_max, 
												eta_min=0, 
												last_epoch=-1)

功能：

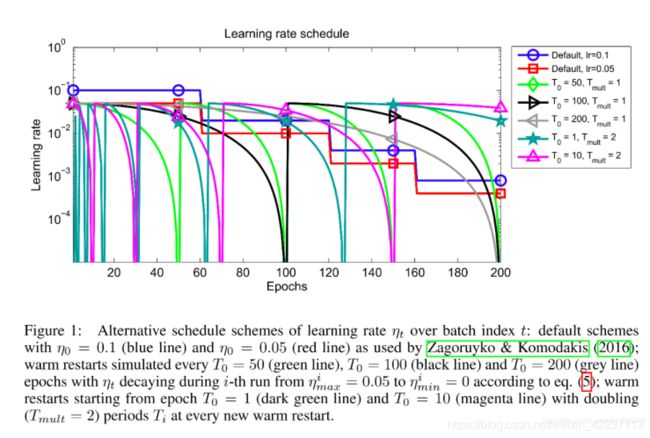
以余弦函数为周期，并在每个周期最大值时重新设置学习率。具体如下图所示

详细请阅读论文《 SGDR: Stochastic Gradient Descent with Warm Restarts》(ICLR-2017)：https://arxiv.org/abs/1608.03983

参数：

T_max(int)- 一次学习率周期的迭代次数，即T_max个epoch之后重新设置学习率。
eta_min(float)- 最小学习率，即在一个周期中，学习率最小会下降到eta_min，默认值为0。

学习率调整公式为：

可以看出是以初始学习率为最大学习率，以2*Tmax为周期，在一个周期内先下降，后上升。

实例：

T_max = 200, 初始学习率 = 0.001, eta_min = 0

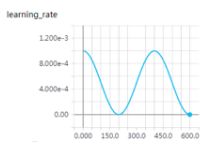
7.1.5.lr_scheduler.ReduceLROnPlateau

class torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, 
                                                mode=‘min’, 
                                                factor=0.1, 
                                                patience=10, 
                                                verbose=False,
                                                threshold=0.0001,
                                                threshold_mode=‘rel’, 
                                                cooldown=0, 
                                                min_lr=0,
                                                eps=1e-08)

功能：

当某指标不再变化（下降或升高），调整学习率，这是非常实用的学习率调整策略。例如，当验证集的loss不再下降时，进行学习率调整；或者监测验证集的accuracy，当accuracy不再上升时，则调整学习率。

参数：

• mode(str)- 模式选择，有 min和max两种模式，min表示当指标不再降低(如监测loss)，max表示当指标不再升高(如监测accuracy)。
• factor(float)- 学习率调整倍数(等同于其它方法的gamma)，即学习率更新为 lr = lr * factor
• patience(int)- 直译——“耐心”，即忍受该指标多少个step不变化，当忍无可忍时，调整学习率。注，可以不是连续5次。
• verbose(bool)- 是否打印学习率信息， print(‘Epoch {:5d}: reducing learning rate’ ’ of group {} to {:.4e}.’.format(epoch, i, new_lr))
• threshold(float)- Threshold for measuring the new optimum，配合threshold_mode使用，默认值1e-4。作用是用来控制当前指标与best指标的差异。
• threshold_mode(str)- 选择判断指标是否达最优的模式，有两种模式，rel和abs。
  当threshold_mode = rel，并且mode = max时，dynamic_threshold = best * ( 1 + threshold )；
  当threshold_mode = rel，并且mode = min时，dynamic_threshold = best * ( 1 - threshold )；
  当threshold_mode = abs，并且mode = max时，dynamic_threshold = best + threshold ；
  当threshold_mode = rel，并且mode = max时，dynamic_threshold = best - threshold
  cooldown(int)- “冷却时间“，当调整学习率之后，让学习率调整策略冷静一下，让模型再训练一段时间，再重启监测模式。
• min_lr(float or list)- 学习率下限，可为float，或者list，当有多个参数组时，可用list进行设置。
• eps(float)- 学习率衰减的最小值，当学习率变化小于eps时，则不调整学习率。

7.1.6.lr_scheduler.LambdaLR

class torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda, last_epoch=-1)

功能：

为不同参数组设定不同学习率调整策略。调整规则为，lr = base_lr * lmbda(self.last_epoch) 。

参数：

lr_lambda(function or list)- 一个计算学习率调整倍数的函数，输入通常为step，当有多个参数组时，设为list。
last_epoch(int)- 上一个epoch数，这个变量用来指示学习率是否需要调整。当last_epoch符合设定的间隔时，就会对学习率进行调整。当为-1时，学习率设置为初始值。

例如：

ignored_params = list(map(id, net.fc3.parameters()))
base_params = filter(lambda p: id§ not in ignored_params, net.parameters())
optimizer = optim.SGD([
{
     ‘params’: base_params},
{
     ‘params’: net.fc3.parameters(), ‘lr’: 0.001*100}], 0.001, momentum=0.9, weight_decay=1e-4)
lambda1 = lambda epoch: epoch // 3
lambda2 = lambda epoch: 0.95 ** epoch
scheduler = torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda=[lambda1, lambda2])
for epoch in range(100):
scheduler.step()
print('epoch: ', i, 'lr: ', scheduler.get_lr())
train(…)
validate(…)

输出：

epoch: 0 lr: [0.0, 0.1]
epoch: 1 lr: [0.0, 0.095]
epoch: 2 lr: [0.0, 0.09025]
epoch: 3 lr: [0.001, 0.0857375]
epoch: 4 lr: [0.001, 0.081450625]
epoch: 5 lr: [0.001, 0.07737809374999999]
epoch: 6 lr: [0.002, 0.07350918906249998]
epoch: 7 lr: [0.002, 0.06983372960937498]
epoch: 8 lr: [0.002, 0.06634204312890622]
epoch: 9 lr: [0.003, 0.0630249409724609]

为什么第一个参数组的学习率会是0呢？ 来看看学习率是如何计算的。
第一个参数组的初始学习率设置为0.001, lambda1 = lambda epoch: epoch // 3,
第1个epoch时，由lr = base_lr * lmbda(self.last_epoch)，可知道 lr = 0.001 * (0//3) ，又因为1//3等于0，所以导致学习率为0。
第二个参数组的学习率变化，就很容易看啦，初始为0.1，lr = 0.1 * 0.95^epoch ，当epoch为0时，lr=0.1 ，epoch为1时，lr=0.1*0.95。

7.2 学习率调整小结及step源码阅读

7.2.1 学习率调整小结

Pytorch提供了六种学习率调整方法，可分为三大类，分别是

• 有序调整；
• 自适应调整；
• 自定义调整。

第一类，依一定规律有序进行调整，这一类是最常用的，分别是等间隔下降(Step)，按需设定下降间隔(MultiStep)，指数下降(Exponential)和CosineAnnealing。这四种方法的调整时机都是人为可控的，也是训练时常用到的。
第二类，依训练状况伺机调整，这就是ReduceLROnPlateau方法。该法通过监测某一指标的变化情况，当该指标不再怎么变化的时候，就是调整学习率的时机，因而属于自适应的调整。
第三类，自定义调整，Lambda。Lambda方法提供的调整策略十分灵活，我们可以为不同的层设定不同的学习率调整方法，这在fine-tune中十分有用，我们不仅可为不同的层设定不同的学习率，还可以为其设定不同的学习率调整策略，简直不能更棒！

7.2.2 step源码阅读

在pytorch中，学习率的更新是通过scheduler.step()，而我们知道影响学习率的一个重要参数就是epoch，而epoch与scheduler.step()是如何关联的呢？这就需要看源码了。
源码在torch/optim/lr_scheduler.py，step()方法在_LRScheduler类当中，该类作为所有学习率调整的基类，其中定义了一些基本方法，如现在要介绍的step()，以及最常用的get_lr()，不过get_lr()是一个虚函数，均需要在派生类中重新定义函数。
看看step()

def step(self, epoch=None):
	if epoch is None:
		epoch = self.last_epoch + 1
		self.last_epoch = epoch
	for param_group, lr in zip(self.optimizer.param_groups, self.get_lr()):
		param_group[‘lr’] = lr

函数接收变量epoch，默认为None，当为None时，epoch = self.last_epoch + 1。从这里知道，last_epoch是用以记录epoch的。上面有提到last_epoch的初始值是-1，因此，第一个epoch的值为 -1+1 =0。接着最重要的一步就是获取学习率，并更新。
由于pytorch是基于参数组的管理方式，这里需要采用for循环对每一个参数组的学习率进行获取及更新。这里需要注意的是get_lr()，get_lr()的功能就是获取当前epoch，该参数组的学习率。

这里以StepLR()为例，介绍get_lr()，请看代码：

def get_lr(self):
	return [base_lr * self.gamma ** (self.last_epoch // self.step_size) for base_lr in self.base_lrs]

由于pytorch是基于参数组的管理方式，可能会有多个参数组，因此用for循环，返回的是一个list。list元素的计算方式为

base_lr * self.gamma ** (self.last_epoch // self.step_size)

看完代码，可以知道，在执行一次scheduler.step()之后，epoch会加1，因此scheduler.step()要放在epoch的for循环当中执行。

7.3 权重正则化

如何解决过拟合问题呢？正则化是其中一个有效方法。正则化不仅可以有效地降低高方差，还有利于降低偏差。
传统意义上的正则化一般分为L0、L1、L2、L∞等。
PyTorch如何实现正则化呢？
这里以实现L2为例，神经网络的L2正则化称为权重衰减（Weight Decay）。torch.optim集成了很多优化器，如SGD、Adadelta、Adam、Adagrad、RMSprop等，这些优化器自带的一个参数weight_decay，用于指定权值衰减率，相当于L2正则化中的λ参数，也就是下式中的λ。

原式：

正则化：

模型训练过程

8. 模型训练和保存

8.1 总体训练过程

层、模型、损失函数和优化器等都定义或创建好，接下来就是训练模型。
训练模型时需要注意使模型处于训练模式，即调用model.train()。调用model.train()会把所有的module设置为训练模式。
如果是测试或验证阶段，需要使模型处于验证阶段，即调用model.eval()，调用model.eval()会把所有的training属性设置为False。

缺省情况下梯度是累加的，需要手工把梯度初始化或清零，调用optimizer.zero_grad()即可。训练过程中，正向传播生成网络的输出，计算输出和实际值之间的损失值。调用loss.backward()自动生成梯度，然后使用optimizer.step（）执行优化器，把梯度传播回每个网络。

如果希望用GPU训练，需要把模型、训练数据、测试数据发送到GPU上，即调用.to(device)。如果需要使用多GPU进行处理，可使模型或相关数据引用nn.DataParallel。

8.2 GPU加速

深度学习涉及很多向量或多矩阵运算，如矩阵相乘、矩阵相加、矩阵-向量乘法等。深层模型的算法，如BP、Auto-Encoder、CNN等，都可以写成矩阵运算的形式，无须写成循环运算。然而，在单核CPU上执行时，矩阵运算会被展开成循环的形式，本质上还是串行执行。图形处理器（GraphicProcess Units，GPU）的众核体系结构包含几千个流处理器，可将矩阵运算并行化执行，大幅缩短计算时间。随着NVIDIA、AMD等公司不断推进其GPU的大规模并行架构，面向通用计算的GPU已成为加速可并行应用程序的重要手段。得益于GPU众核（Many-Core）的体系结构，程序在GPU系统上的运行速度相较于单核CPU往往提升了几十倍乃至上千倍。

目前，GPU已经发展到了较为成熟的阶段。利用GPU来训练深度神经网络，可以充分发挥其数以千计的计算核心的能力，在使用海量训练数据的场景下，所耗费的时间大幅缩短，占用的服务器也更少。如果对适当的深度神经网络进行合理优化，一块GPU卡可能相当于数十甚至上百台CPU服务器的计算能力，因此GPU已经成为业界在深度学习模型训练方面的首选解决方案。

如何使用GPU？
现在很多深度学习工具都支持GPU运算，使用时只要简单配置即可。PyTorch支持GPU，可以通过to（device）函数来将数据从内存中转移到GPU显存，如果有多个GPU还可以定位到哪个或哪些GPU。
PyTorch一般把GPU作用于张量（Tensor）或模型（包括torch.nn下面的一些网络模型以及自己创建的模型）等数据结构上。

8.2.3 单GPU

使用GPU之前，需要确保GPU是可以使用的，可通过torch.cuda.is_available()方法的返回值来进行判断。返回True则具有能够使用的GPU。
通过torch.cuda.device_count()方法可以获得能够使用的GPU数量。

如何查看平台GPU的配置信息？
在命令行输入命令“nvidia-smi”即可（适合于Linux或Windows环境）。

把数据从内存转移到GPU，一般针对张量（我们需要的数据）和模型。对张量（类型为FloatTensor或者是LongTensor等），一律直接使用方法.to(device)或.cuda()。

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
#或device = torch.device("cuda:0")
device1 = torch.device("cuda:1")
for batch_idx, (img, label) in enumerate(train_loader):
	img=img.to(device)
	label=label.to(device)

对于模型来说，也是同样的方式，使用.to(device)或.cuda来将网络放到GPU显存。

#实例化网络
model = Net()
model.to(device) #使用序号为0的GPU
#或model.to(device1) #使用序号为1的GPU

8.2.4 多GPU模式

这里主要介绍单主机多GPU的情况，单机多GPU主要采用了DataParallel函数，而不是DistributedParallel，后者一般用于多主机多GPU，当然也可用于单机多GPU。使用多卡训练的方式有很多，当然前提是我们的设备中存在两个及以上的GPU。

使用时直接用model传入torch.nn.DataParallel函数即可，代码如下所示：

#多模型
net = torch.nn.DataParallel(model)

这时，默认所有存在的显卡都会被使用。
如果你的电脑有很多显卡，但只想利用其中一部分，如只使用编号为
0、1、3、4的4个GPU，那么可以采用以下方式：

#假设有4个GPU,其id设置如下
device_ids =[0,1,2,3]
#对数据
input_data=input_data.to(device=device_ids[0])
#对于模型
net = torch.nn.DataParallel(model)
net.to(device)

或者

os.environ["CUDA_VISIBLE_DEVICES"] = ','.join(map(str, [0,1,2,3]))
net = torch.nn.DataParallel(model)

其中CUDA_VISIBLE_DEVICES表示当前可以被PyTorch程序检测到的GPU。下面为单机多GPU的实现代码：
1）背景说明。
这里使用波士顿房价数据为例，共506个样本，13个特征。数据划分成训练集和测试集，然后用data.DataLoader转换为可批加载的方式。采用nn.DataParallel并发机制，环境有2个GPU。当然，数据量很小，按理不宜用nn.DataParallel，这里只是为了更好地说明使用方法
2）加载数据

boston = load_boston()
X,y = (boston.data, boston.target)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
#组合训练数据及标签
myset = list(zip(X_train,y_train))

3）把数据转换为批处理加载方式。
批次大小为128，打乱数据。

from torch.utils import data
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
dtype = torch.FloatTensor
train_loader = data.DataLoader(myset,batch_size=128,shuffle=True)

4）定义网络

class Net1(nn.Module):
"""
使用sequential构建网络，Sequential()函数的功能是将网络的层组合到一起
"""
	def __init__(self, in_dim, n_hidden_1, n_hidden_2, out_dim):
		super(Net1, self).__init__()
			self.layer1 = torch.nn.Sequential(nn.Linear(in_dim, n_hidden_1))
			self.layer2 = torch.nn.Sequential(nn.Linear(n_hidden_1, n_hidden_2))
			self.layer3 = torch.nn.Sequential(nn.Linear(n_hidden_2, out_dim))	
	def forward(self, x):
		x1 = F.relu(self.layer1(x))
		x1 = F.relu(self.layer2(x1))
		x2 = self.layer3(x1)
		#显示每个GPU分配的数据大小
		print("\tIn Model: input size", x.size(),"output size", x2.size())
	return x2

5）把模型转换为多GPU并发处理格式

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
#实例化网络
model = Net1(13, 16, 32, 1)
if torch.cuda.device_count() > 1:
	print("Let's use", torch.cuda.device_count(), "GPUs")
	# dim = 0 [64, xxx] -> [32, ...], [32, ...] on 2GPUs
	model = nn.DataParallel(model)
model.to(device)

运行结果：

Let's use 2 GPUs
DataParallel(
(module): Net1(
		(layer1): Sequential(
			(0): Linear(in_features=13, out_features=16, bias=True)
		)
		(layer2): Sequential(
			(0): Linear(in_features=16, out_features=32, bias=True)
		)
		(layer3): Sequential(
			(0): Linear(in_features=32, out_features=1, bias=True)
		)
	)
)

6）选择优化器及损失函数。

optimizer_orig = torch.optim.Adam(model.parameters(), lr=0.01)
loss_func = torch.nn.MSELoss()

7）模型训练，并可视化损失值。

from tensorboardX import SummaryWriter
writer = SummaryWriter(log_dir='logs')
for epoch in range(100):
	model.train()
	for data,label in train_loader:
		input = data.type(dtype).to(device)
		label = label.type(dtype).to(device)
		output = model(input)
		loss = loss_func(output, label)
		# 反向传播
		optimizer_orig.zero_grad()
		loss.backward()
		optimizer_orig.step()
		print("Outside: input size", input.size() ,"output_size", output.size())
	writer.add_scalar('train_loss_paral',loss, epoch)

运行的部分结果：

In Model: input size torch.Size([64, 13]) output size torch.Size([64,
1]) In Model: input size torch.Size([64, 13]) output size
torch.Size([64, 1]) Outside: input size torch.Size([128, 13])
output_size torch.Size([128, 1]) In Model: input size torch.Size([64,
13]) output size torch.Size([64, 1]) In Model: input size
torch.Size([64, 13]) output size torch.Size([64, 1]) Outside: input
size torch.Size([128, 13]) output_size torch.Size([128, 1])

从运行结果可以看出，一个批次数据（batch-size=128）拆分成两份，
每份大小为64，分别放在不同的GPU上。此时用GPU监控也可发现，两个
GPU都同时在使用，如下图所示。

8）通过web查看损失值的变化情况，如下图所示。

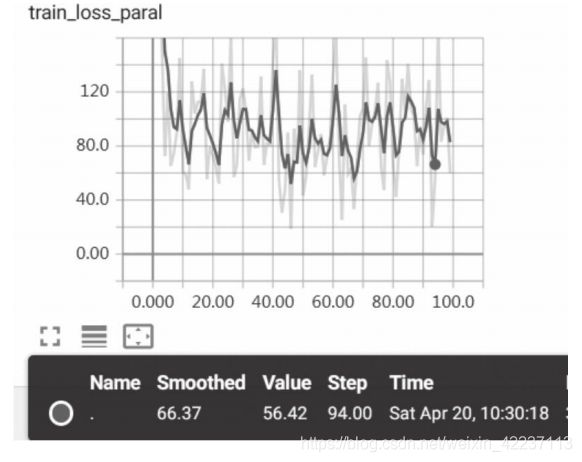
图出现较大振幅，是由于采用批次处理，而且数据没有做任何预处理，因此对数据进行规范化应该更平滑一些，读者可以尝试一下。

单机多GPU也可使用DistributedParallel，它多用于分布式训练，但也可以用在单机多GPU的训练，配置比使用nn.DataParallel稍微麻烦一点，但是训练速度和效果更好一点。具体配置为：

#初始化使用nccl后端
torch.distributed.init_process_group(backend="nccl")
#模型并行化
model=torch.nn.parallel.DistributedDataParallel(model)

单机运行时使用下列方法启动：

python -m torch.distributed.launch main.py

9 pytorch通用模板

pytorch代码都是按照一定套路修改的，最后附上别人总结的通用模板， 各位enjoy~:

# 详情参考：https://www.jianshu.com/p/e606f8fc1626
"""
GPU加速
dropout
批标准化处理
优化器
激活函数
"""
import torch
import torch.nn.functional as F
import torch.nn as nn
import torch.utils.data as Data

#定义参数
BATCH_SIZE = 64  # 在Data中
EPOCHS = 50  # 迭代次数
LR = 0.05  # 学习率
OUTPUT = 0.5  # dropout百分比

######################构建torch神经网络######################
# 1.获取数据
    #数据库 / excel
# 2.处理数据
    #数据的异常值，缺失值，数据转换等特征工程
    #最终获取：train_x,train_y test_x,test_y
# 3.利用Data处理数据 固定模板
train_dataset = Data.TensorDataset(train_x, train_y)
train_loader = Data.DataLoader(dataset=train_dataset, 
                               batch_size=BATCH_SIZE, 
                               shuffle=True, 
                               num_workers=2,)

# 4.构建神经网络模型 这部分是核心部分
class Net(nn.Module):
    def __init__(self, batch_normalization=False):
        super(Net, self).__init__()
        pass

    def forward(self, x):
        
        pass
    
# 5.构建优化函数和损失函数
net = Net()
opts = torch.optim.Adam(net.parameters(), lr=LR)  # 这里的LR是定义的学习率
loss_func = torch.nn.MSELoss()   # 这只是一种损失函数

# 6.训练
for epoch in range(EPOCHS):    # 迭代次数EPOCHS
    for step, (batch_x, batch_y) in enumerate(train_loader):  # 分批次训练
        pred= net(batch_x)  # 训练模型
        # 下面是固定模板
        loss = loss_func(pred, batch_y) # 计算损失值
        opts.zero_grad()  # 清除这次训练的梯度  （因为梯度是累加的）
        loss_func.backward() #  计算梯度
        opts.step() #应用梯度

# 7.模型预测
# 预测test_x数据对应的前10
test_output = net(test_x[:10])
pred_y = torch.max(test_output, 1)[1].data.numpy()
print(pred_y, 'prediction number')
print(test_y[:10].numpy(), 'real number')

# 8.1 模型的保存和加载--保存完整的神经网络
torch.save(net, 'net.pkl')
net = torch.load('net.pkl')
# 8.2 模型的保存和加载--只保存神经网络参数，使用的时候需要加载模型的框架
torch.save(net.state_dict(), 'net_params.pkl')  
net = Net() # 模型框架
net.load_state_dict(torch.load('net_params.pkl'))

Reference:

too many~~