人工智能 遗传算法 计算函数极值问题

人工智能 遗传算法 计算函数极值问题

---

系列文章

• 人工智能 倒啤酒问题 python解法
• 人工智能 水壶问题 python解法
• A*算法之八数码问题 python解法
• A*算法之野人传教士问题 python解法
• 人工智能 遗传算法 计算函数极值问题

---

---

学习了遗传算法之后,感觉掌握的不是很透彻,所以打算写篇文章先记录一下

间隔了好久,发现遗传算法(这篇文章)忘记发了,就加上了代码今天发了出来

问题描述

使用遗传算法求解三元函数z的最大值
$$z=f(x,y)=1\ast x\ast sin(4\pi x)-1\ast y\ast sin(4\pi y+\pi )+1$$
其中 x,y的定义域都为 (-1 , 1 )
实验要求：

• 编码、初始群体的产生、适应度计算、选择运算、交叉运算、变异运算说明
• x,y定义域值编码采用二进制编码，各自用15位编码。

遗传算法介绍

主要来介绍一下遗传算法的大题思路

在网上查了一对资料之后,可算是稍微知道了一些遗传算法的特性
这里我就稍微总结一下大致的流程,官方的解析还是去百度搜搜大佬们的回答比较好

【算法】超详细的遗传算法Genetic
之前几篇文章的搜索算法都有着一个特性,遗传算法也不例外,他们的总体流程我认为都是一样的

1.构造初始状态

在一些搜索算法中体现为创建open表,而遗传算法当中成为构造初始种群
虽然叫法不同,但是都是对于整个算法的初始化,可以理解为把我们需要考虑的节点全部放到一个列表当中

2.构造算子

这一步其实应该算是准备工作,不过站在编程的角度,我就把它放在第二点了
在之前的搜索算法中,如八数码问题, 我们的算子就是空格的上下左右移动四种
而在倒啤酒问题当中,算子就是A瓶子倒空,倒满,倒入B瓶子等等
在遗传算法里面,算子就结合了遗传学(学过高中生物的应该都知道)
1. 复制 (将DNA一模一样复制一份)
2.交叉互换 (将DNA上的基因交叉互换,这部分可以百度搜索)
3.变异 (DNA上的部分基因突变成新的基因)

上面的例子是针对生物学来说的,那么遗传算法里哪来的DNA呢,这就需要讲到我认为遗传算法里面不同于其他算法的第一点: 编码
对于单纯的数字 比如 1,2,3,4,5 我们很难想到一个好的方法对它们来实现交叉互换或者变异的操作
而对于二进制编码,就方便多了
比如我们现在有一串二进制数字
00111100与10110010
我们可以从中间将它们划分,把每四位都看成一个基因0011 1100 ,1011 0010

• 那么基因交换就可以表示为第一个数的左边四位与第二个数的右边四位交换(也可以是右边四边,这个随机产生)
• 而基因突变也可以表示为其中的一个二进制从0变成1或者从1变成0

那么如何把(-1,1)这个定义域转换成二进制编码呢

3.编码

为了更好的实现三种算子的操作,引入了编码的概念,在本次实验中,我们使用的是二进制编码
本题x,y的范围是(-1,1) 而编码就是将(-1,1)区间内的数字用二进制来表示
那么问题来了,(-1,1)如何使用二进制来表示
从最简单的例子来说,2位的二进制可以表示 $2^2$个数字,如果我们用2位编码来表示(-1,1)之间的数字,那么我们可能只能表示$$-1,-\frac{1}{3},-\frac{1}{3},1$$
计算方法如下
$$d=-\frac{(1-(-1))}{2^2-1}$$
$$a_1=-1$$
$$a_2=-1+d$$
$$a_3=-1+2d$$
$$a_4=-1+3d$$
这样四个数,显然是不够的,所以我们需要2进制的个数越来越多,才可以把区间表示的更加精确
我们发现题目中给出了一个限制 x,y定义域值编码采用二进制编码，各自用15位编码,所以本题我们可以使用15位二进制来对(-1,1)之间的数字来编码,也就是分为32767个区间(32768个点)
$$2^{15}=32768$$
那么如何编码和解码就很清晰了

4 启发式函数

在搜索算法中,启发式函数启动了非常重要的作用,大大提升了效率,在A*算法中,每次算子操作结束后,我们都会将合适的节点插入open表,然后用启发式函数的值对open表进行排序,在下一轮的迭代中可以从最优的节点开始

在遗传算法中使用轮盘选择法,稍有不同,但是本质的原理也是一样的
遗传算法中的启发式函数是为了让优秀的基因保留下来的概率变大,在这里采用了轮盘选择法
通俗的解释就是:在初始化种群之后,使用启发式函数计算每个基因的优秀程度,然后为他们分配一个保留下来的概率

比如有 a,b,c,d四个基因,通过启发式函数(这里假设越大越好),计算出来的值是1,2,3,4
那么他们的概率就是$\frac{1}{1+2+3+4}$,$\frac{2}{1+2+3+4}$,$\frac{3}{1+2+3+4}$,$\frac{4}{1+2+3+4}$
这很好理解吧,相当于每个基因都有留下来的概率

5.遗传算法与函数极值问题解决

再简单的讲述一下题目:
$$z=f(x,y)=1\ast x\ast sin(4\pi x)-1\ast y\ast sin(4\pi y+\pi )+1$$
当$x\in (-1,1),y\in (-1,1)$时,求一组x, y的取值 使得z最大

乍一看不就是个数学题,求两个偏导等于0不就完事了
不过我们要用编程来实现,还得用遗传算法,就很头秃了
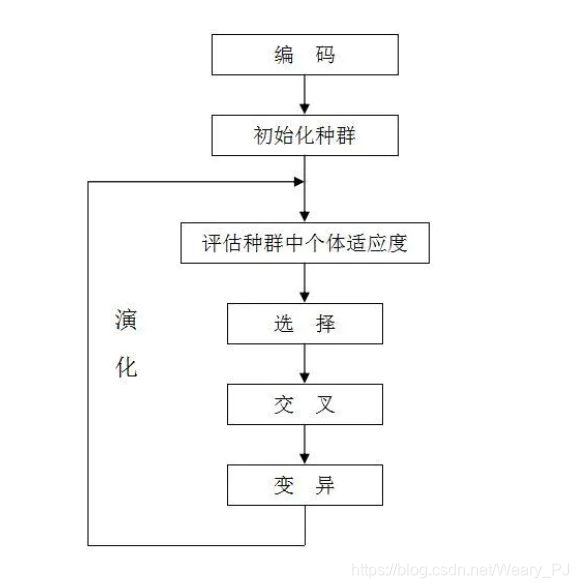
一步步来呗,再看一眼流程图

初始化种群

编写一个函数来初始化种群

def init_population():
	pass

解码

这里我们需要编写一个函数,能把二进制的数字转换回(-1,1)的区间内

# 解码
def To_decode(num):
	# num是二进制数 需要返回一个区间内的小数
	pass

算子

编写一个函数包含三种算子的操作

def gene_operation():
	pass

评估函数

编写一个函数来评估种群中个体的价值

def estimate():
	pass

函数框架

b = 预计循环的轮数
for i in range(n):
	tribe= init_population() # 初始化种群(部落)
	tribe_value= estimate(tribe) # 每个个体的价值(概率)
	for action in actions: # 三种算子的操作
		tribe = gene_operation(tribe,tribe_value,type=action)
# 循环结束,得到最终优秀的tribe 
# 找到里面 value最大的情况即可

已经有文章解决了这个问题
遗传算法求函数最值python解法

遗传算法编程

代码的思路都写在每个函数的注释里了

# -*- coding: utf-8 -*-  
# @Time    : 2020/11/28 9:16  
# @Author  : Tong Tianyu  
# @File    : 遗传算法_函数极大值问题.py  
import random  
from math import fabs, sin, pi  
import numpy as np  
import prettytable as pt  
  
'''''题目要求'''  
# z=f(x,y)=1*x*sin(4πx)-1*y*sin(4πy+π)+1  
# 在-1
# 实验要求：  
# 编码、初始群体的产生、适应度计算、选择运算、交叉运算、变异运算  
# 说明，x,y定义域值编码采用二进制编码，各自用15位编码。  
'''''定义全局变量'''  
max_loop = 200  # 最大迭代次数 100~500  
tribe_number = 50  # 种群初始化数量 20~100  
limit_left = -1  # 定义域左界限  
limit_right = 1  # 定义域右界限  
limit_bit = 15  # 编码位数  
cross_probability = 0.7  # 交叉概率 0.4~0.99  
variation_probability = 0.01  # 变异概率 0.0001~0.1  
copy_probability = 1 - cross_probability - variation_probability  # 复制概率  
actions_probability = np.array([copy_probability, cross_probability, variation_probability])  
  
  
# 进制转换  
def To_decode(num):  
    ''''' 
    num是二进制数  用列表表示 长度为30 
    :param num: 
    :return: 返回x,y对应的(-1,1)区间小数 
    '''  
    # 分割数组  
    x = num[:15]  
    y = num[15:]  
    # 转为10进制整数  
    x = int(str(x), 2)  
    y = int(str(y), 2)  
    # 转换为-1,1区间的小数  
    d = fabs(limit_left - limit_right) / (2 ** limit_bit - 1)  
    x = limit_left + d * x  
    y = limit_left + d * y  
    return x, y  
  
  
# 初始化一个个体  
def init_one(bit=30):  
    ''''' 
    返回一个 bit位数的二进制串 
    :param bit: 位数 
    :return: 
    '''  
    s = ''  
    for i in range(bit):  
        s += str(random.randint(0, 1))  
    return s  
  
  
# 初始化一个种群  
def init_tribe(tribe_number):  
    ''''' 
    初始化一个种群 
    :param tribe_number: 种群个数 
    :return: 
    '''  
    tribe = []  
    while len(set(tribe)) != tribe_number:  
        tribe.append(init_one())  
    return tribe  
  
  
# 返回被选择的种群  
def roulette_select_tribe(value, tribe):  
    ''''' 
    轮盘选择: 根据概率选择出个体, 返回选择后的种群 
    这里优化了一个操作,就是始终会将 启发值最大的节点加入选择后的种群 
    :param value: 传入参数: 代表每个个体被选择的概率 
    :param tribe: 传入参数: 代表种群的信息 
    :return: 
    '''  
    new_tribe = []  
    # 设置随机数种子  
    np.random.seed(random.randint(1, 100) + random.randint(100, 10000000))  
    index_list = [i for i in range(tribe_number)]  
    for i in range(tribe_number):  
        # 根据概率获取索引  
        index = np.random.choice(index_list, p=value.ravel())  
        new_tribe.append(tribe[index])  
    # 判断启发值最大的节点是否被加入  
    li = list(value)  
    max_index = li.index(max(li))  
    if tribe[max_index] not in new_tribe:  
        tmp_value = list(estimate(new_tribe))  
        min_index = tmp_value.index(min(tmp_value))  
        new_tribe[min_index] = tribe[max_index]  
    return new_tribe  
  
  
# 返回被选择的个体索引(下标)  
def roulette_select_human(value, tribe):  
    ''''' 
    轮盘选择: 根据概率选择出个体, 返回一个被选择的对象与其索引 
    :param value: 传入参数: 代表每个个体被选择的概率 
    :param tribe: 传入参数: 代表种群的信息 
    :return: 
    '''  
    np.random.seed(random.randint(1, 100) + random.randint(100, 10000000))  
    index_list = [i for i in range(tribe_number)]  
    index = np.random.choice(index_list, p=value.ravel())  
    return tribe[index], index  
  
  
# 评估每个个体被选择的概率  
def estimate(tribe):  
    ''''' 
    返回一个 numpy.array类型的 概率数组,代表了tribe中每一个个体被选中的概率 
    :param tribe: 
    :return: 
    '''  
    start_value = []  
    for human in tribe:  
        x, y = To_decode(human)  
        human_value = 1 * x * sin(4 * pi * x) - 1 * y * sin(4 * pi * y + pi) + 1  
        start_value.append(human_value if human_value > 0 else 0)  
    # 将列表中的每个value转换为相应的概率  
    result_value = [i / sum(start_value) for i in start_value]  
    return np.array(result_value)  
  
  
def cal_func(human):  
    ''''' 
    计算单个个体的启发值 (也就是函数的值) 
    :param human: 
    :return: 
    '''  
    x, y = To_decode(human)  
    human_value = 1 * x * sin(4 * pi * x) - y * sin(4 * pi * y + pi) + 1  
    return human_value  
  
  
def gene_operation(tribe, type):  
    ''''' 
    进行复制,交叉,变异的操作 
    :param tribe: 
    :param type: 
    :return: 
    '''  
    if type == '复制':  
        return tribe  
    if type == '交叉':  
        # 初始化需要的参数  
        value = estimate(tribe)  
        cross_tmp = []  
        # 随机选择父母节点  
        father, father_index = roulette_select_human(value, tribe)  
        mother, mother_index = roulette_select_human(value, tribe)  
        # 随机确定 交叉点  
        cross_location = random.randint(0, 29)  
        cross_tmp.append(cross_location)  
        # 执行交叉操作  
        infant = father[0:cross_location] + mother[cross_location:]  
        # 计算其评估值是否变优秀,没有变优秀就重来  
        score = cal_func(infant) - cal_func(father)  
        while score < 0:  
            if len(cross_tmp) == 30:  
                return tribe  
            cross_location = random.randint(0, 29)  
            if cross_location in cross_tmp:  
                continue  
            cross_tmp.append(cross_location)  
            infant = father[0:cross_location] + mother[cross_location:]  
            score = cal_func(infant) - cal_func(father)  
        # 修改tribe (将交叉后的结果与原先的节点替换/不变)  
        tribe[father_index] = infant  
        return tribe  
    if type == '突变':  
        # 初始化需要的参数  
        value = estimate(tribe)  
        # 随机选择变异节点  
        variation_human, variation_human_index = roulette_select_human(value, tribe)  
        tmp_human = variation_human  
        # 随机选择变异位置  
        variation_location = random.randint(0, 29)  
        # 取反  
        num = 1 - int(variation_human[variation_location])  
        tmp = list(variation_human)  
        tmp[variation_location] = str(num)  
        variation_human = ''.join(tmp)  
        # 判断是否有效  
        if cal_func(variation_human) < cal_func(tmp_human):  
            tribe[variation_human_index] = variation_human  
        return tribe  
  
  
def gene_func():  
    actions = ['复制', '交叉', '突变']  
    tribe = init_tribe(tribe_number)  # 初始化种群(部落)  
    for i in range(max_loop):  
        print(f'------------------第{i + 1}轮-----------------')  
        tribe_value = estimate(tribe)  # 启发式函数计算每个个体的价值(概率)  
        tribe = roulette_select_tribe(tribe_value, tribe)  # 轮盘选择后的种群  
        for human in tribe:  
            # 设置随机数种子  
            np.random.seed(random.randint(1, 100) + random.randint(100, 10000000))  
            # 获取该节点将进行的操作(复制,交叉,变异)  
            index = np.random.choice([0, 1, 2], p=actions_probability.ravel())  
            type = actions[index]  
            # 进行个体基因操作  
            tribe = gene_operation(tribe, type=type)  
        # 输出一下该轮结束后的最大值是什么  
        result_value = list(estimate(tribe))  
        result_index = result_value.index(max(result_value))  
        print('max_Z= ', cal_func(tribe[result_index]))  
    # 循环结束,得到最终优秀的tribe  
    # 找到里面 value最大的情况即可  
    print('循环结束')  
    tb = pt.PrettyTable()  
    tb.field_names = ['函数极大值', 'x编码', 'y编码', 'x真值', 'y真值']  
    result_value = list(estimate(tribe))  
    result_index = result_value.index(max(result_value))  
    max_result = cal_func(tribe[result_index])  
    x, y = To_decode(tribe[result_index])  
    tb.add_row([max_result, tribe[result_index][:15], tribe[result_index][15:], x, y])  
    print(tb)  
  
  
if __name__ == '__main__':  
    gene_func()