《PlaneNet-单幅RGB图像的分段平面重建》论文中英文对照解读
论文地址:https://arxiv.org/pdf/1804.06278.pdf
代码地址:https://github.com/art-programmer/PlaneNet
PlaneNet: Piece-wise Planar Reconstruction from a Single RGB Image
PlaneNet:单幅RGB图像的分割平面重建
Abstract
论文摘要
EN: This paper proposes a deep neural network (DNN) for piece-wise planar depthmap reconstruction from a single RGB image. While DNNs have brought remarkable progress to single-image depth prediction, piece-wise planar depthmap reconstruction requires a structured geometry representation, and has been a difficult task to master even for DNNs. The proposed end-to-end DNN learns to directly infer a set of plane parameters and corresponding plane segmentation masks from a single RGB image. We have generated more than 50,000 piece-wise planar depthmaps for training and testing from ScanNet, a largescale RGBD video database. Our qualitative and quantitative evaluations demonstrate that the proposed approach outperforms baseline methods in terms of both plane segmentation and depth estimation accuracy. To the best of our knowledge, this paper presents the first end-to-end neural architecture for piece-wise planar reconstruction from a single RGB image. Code and data are available at https://github.com/art-programmer/PlaneNet.
CH: 本篇论文提出了一种深度神经网络(DNN)去完成单幅图像的分割平面深度图重建任务。虽然DNN在单幅图像上的深度预测取得了显著的进步,但是分割平面深度图重建需要一个结构化的几何表示,即使对于DNN也是很难解决的一个任务。提出的这个端到端的DNN直接从单幅RGB图像中推算出一套平面参数和对应的平面分割掩膜。我们从 ScanNet 生成了超过50000张的分割平面深度图用于训练和测试,ScanNet 是一个大型的 RGBD 视频数据集。我们的定性和定量评估表明我们提出的这个方法在平面分割和深度估计的精度方面都比基础的方法效果要好。据我们所知,这篇论文提出的端到端神经网络结构是第一个用来解决单幅RGB图像的分割平面重建问题的神经网络。代码和数据均在GitHub:https://github.com/art-programmer/PlaneNet
1. Introduction
1. 前言
EN: Human vision has extraordinary perceptual power in understanding advanced scene structures. Looking at a typical indoor scene (for example, Figure 1), we can immediately parse the room into a few major planes (for example, floors, walls, and ceilings), sense the main surface of the furniture, or identify the surface of a horizontal tabletop. Segmental planar geometry understanding will be key to many applications in emerging areas such as robotics or augmented reality (AR). For example, the robot needs to identify the extent of the floor used to plan the move, or the desktop split for placing the object. In AR applications, planar surface inspection is becoming the basic building block for placing virtual objects on the desktop, replacing floor textures or hanging artwork on walls for internal remodeling. A fundamental problem in computer vision is the development of a computational algorithm that masters similar perceptions to implement such an application.
CH: 人类视觉在理解高级别场景结构方面有着非凡的感知能力。看一个典型的室内场景(比如图一),我们能立即将这个房间分析成一些主要的平面(比如墙,地板,天花板),感知家具的主要表面和水平桌面的表面。分割平面的几何理解对一些新兴领域的许多应用起到了很关键的作用,比如机器人或虚拟现实(AR)。例如,机器人需要检测用于移动的地板的范围,或者在放置物体时需要分割桌面。在AR应用中,需要往桌面上放置虚拟的物体,更换地板的样式或对墙上的艺术品进行内部改建,这时的检测平面的表面就是一个基础的模块。计算机视觉中一个基础的问题是一个能解决相似感知问题的几何算法来实现这样的应用。
EN: With the proliferation of deep neural networks, single image depth map inference and room layout estimation have been active areas of research. However, to our surprise, little attention has been paid to the study of segmental planar depth map reconstruction, which mimics this remarkable human perception in a general form. The main challenge is that segmented planar depth maps require a structured geometric representation (ie, a set of planar parameters and their segmentation masks). In particular, we do not know the number of planes to infer, and the order of the planes that are returned in the output feature vector, making the task even challenging for deep neural networks.
CH: 随着深度神经网络的兴起,单幅图像的深度图和房间布局的推断一直是搞研究的活跃领域。然而,我们感到比较惊讶的是,分割平面深度图重建这一方面很少有人关注,这一方面一般来说是模仿了人类的这种非凡的感知能力。其中比较主要的挑战是分割平面深度图需要一个结构化的几何表示(i.e.平面参数的集合和它们的分割掩膜)。尤其是,我们不知道需要分割的平面数量,以及平面在输出特征向量中的顺序,完成这些任务对深度神经网络来说也很有挑战。
EN: This paper proposes a novel deep neural architecture “PlaneNet” that learns to directly produce a set of plane parameters and probabilistic plane segmentation masks from a single RGB image. Following a recent work on point-setgeneration, we define a loss function that is agnostic to the order of planes. We further control the number of planes by allowing probabilistic plane segmentation masks to be all 0. The network also predicts a depthmap at non-planar surfaces, whose loss is defined through the probabilistic segmentation masks to allow back-propagation. We have generated more than 50,000 piece-wise planar depthmaps from ScanNet as ground-truth by fitting planes to 3D points and projecting them to images. Qualitative and quantitative evaluations show that our algorithm produces significantly better plane segmentation results than the current state-ofthe-art. Furthermore, our depth prediction accuracy is on-par or even superior to the existing single image depth inference techniques that are specifically trained for this task.
CH: 本篇论文提出了一个新的深度神经网络结构“PlaneNet”,它通过学习训练直接从单幅RGB图像中得到一组平面参数和对应的平面分割掩膜。在最近的一项点集分割工作中,我们定义了一个跟平面顺序无关的损失函数。我们通过允许概率性的平面分割掩膜为0来进一步的控制平面的数量。这个网络结构还预测非平面处的深度图,这个损失是通过概率分割掩膜定义的,可以进行反向传播。我们通过拟合平面到3D点上,并且将它们投射到图像中,从 ScanNet 数据集中生成了超过50000张分段平面深度图作为真实样本。定性和定量的评估标准表明:我们的算法的平面分割结果相比当下流行的技术,有显著的提升。此外,我们的深度预测精度甚至要比当下专门针对此任务的算法更优秀。
2. Related work
2. 相关工作
EN: Multi-view piece-wise planar reconstruction. Piece-wise planar depthmap reconstruction was once an active research topic in multi-view 3D reconstruction. The task is to infer a set of plane parameters and assign a plane ID to each pixel. Most existing methods first reconstruct precise 3D points, perform plane-fitting to generate plane hypotheses, then solve a global inference problem to reconstruct a piece-wise planar depthmap. Our approach learns to directly infer plane parameters and plane segmentations from a single RGB image.
CH: 多视图分段平面重建。分段平面深度图重建曾经在多视图3D重建中的活跃研究领域。这个任务是推断一组平面参数并且给每个像素分配一个平面ID。目前大部分的算法都是首先重建精确的3D点集,拟合平面去生成假设平面,然后求解一个全局的推理问题去重建一个分段平面深度图。我们的方法通过学习训练直接从单幅RGB图像中得到一组平面参数和对应的平面分割掩膜。
EN: Learning based depth reconstruction. Saxena et al. pioneered a learning based approach for depthmap inference from a single image. With the surge of deep neural networks, numerous CNN based approaches have been proposed. However, most techniques simply produce an array of depth values (i.e., depthmap) without plane detection or segmentation. More recently, Wang et al. enforce planarity in depth (and surface normal) predictions by inferring pixels on planar surfaces. This is the closest work to ours. However, they only produce a binary segmentation mask (i.e., if a pixel is on a planar surface or not) without plane parameters or instance-level plane segmentation.
CH: 基于自学习的深度重建。Saxena 等人针对单幅图像的深度图推断提出了一个基于自学习的方法。随着深度神经网络的兴起,出现了许多基于CNN的方法。但是,大部分的方法只是简单生成一组深度数值(i.e.深度图)而没有平面的检测与分割。最近,Wang等人通过计算平面上的像素信息,在深度信息(以及表面法线)预测中执行平面化操作。这是跟我们最接近的方法。然而,他们仅仅生成一个二进制的分割掩膜(i.e.一个像素是否在平面上),而没有平面参数或实例级别的平面分割。
EN: Layout estimation. Room layout estimation also aims at predicting dominant planes in a scene (e.g., walls, floor, and ceiling). Most traditional approaches rely on image processing heuristics to estimate vanishing points of a scene, and aggregate low-level features by a global optimization procedure. Besides low-level features, high-level information has been utilized, such as human poses or semantics. Attempts have been made to go beyond room structure, and predict object geometry. However, the reliance on hand-crafted features makes those methods less robust, and the Manhattan World assumption limits their operating ranges. Recently, Lee et al. proposed an end-to-end deep neural network, RoomNet, which simultaneously classifies a room layout type and predicts corner locations. However, their framework is not applicable to general piece-wise planar scenes.
CH: 房间布局估计。房间布局的估计也是针对一个场景中的主要平面进行预测的。(e.g.墙,地板和天花板)大部分传统的算法依靠图像的启发式处理去估算场景中的消隐点,并通过一个全局的优化程序聚合底层特征。除了底层特征,还使用到了一些高级信息,比如:人类的姿态和语义。尝试越过房间的结构来预测目标的几何结构。但是,人工选择的特征使得这些方法的稳健性比较低,曼哈顿世界的假设也限制了它们的操作范围。最近,Lee等人,提出了一个端到端的深度神经网络 RoomNet,它能同时分类房间的布局类型和预测角落的位置。但是,他们的框架不适用与一般情况下的分段平面场景。
EN: Line analysis. Single image 3D reconstruction of line drawings date back to the 60s. The earliest attempt is probably the Robert’s system, which inspired many follow-up works. In real images, extraction of line drawings is challenging. Statistical analysis of line directions, junctions, or image segments have been used to enable 3D reconstruction for architectural scenes or indoor panoramas. Attributed grammar was used to parse an image into a hierarchical graph for 3D reconstruction. However, these approaches require hand-crafted features, grammar specification, or algorithmic rules. Our approach is purely data-driven harnessing the power of deep neural networks.
CH: 线分析。单幅线条图像的3D重建可以追溯到60年代。最早的尝试大概是 Robert 的系统,它启发了许多后面的工作。在实际的图像中,线条图的提取有不小的挑战性。线向统计分析,交叉点和图像分割已经被用于建筑场景和室内全景图的3D重建。Attributed grammar 将图像解析成分层图用于3D重建。但是,这些传统的算法需要人工选取的特征,grammar specification, 或算法规则。我们的方法纯粹靠数据驱动的深度神经网络的力量。
3. PlaneNet
3. PlaneNet
EN: We build our network on the Extended Residual Network (DRN) (see Figure 2), which is a flexible framework for global tasks (eg image classification) and pixel prediction tasks (eg semantic segmentation). Given the high-resolution final feature map from the DRN, we make three output branches for the three prediction tasks.
CH: 我们基于 Extended Residual Network (DRN) 来构建我们的网络,(图二所示)DRN是针对全局性任务(e.g.图片分类)和像素预测任务(e.g.语义分割)的一个灵活框架。针对DRN最终输出的高分辨率的特征图,我们对于三个不同的预测任务提供了三个分支。

EN: Plane parameters: For each scene, we predict a fixed number ( K K K) of planar surfaces S = S 1 , ⋅ ⋅ ⋅ S K S = {S_1, · · · S_K} S=S1,⋅⋅⋅SK. Each surface S i S_i Si is specified by the three plane parameters P i P_i Pi (i.e., encoding a normal and an offset). We use D i D_i Di to denote a depth image, which can be inferred from the parameters P i P_i Pi .The depth value calculation requires camera intrinsic parameters, which can be estimated via vanishing point analysis, for example. In our experiments, intrinsics are given for each image through the database information.
CH: 平面参数。对于每个场景,我们预测的平面 S = S 1 , ⋅ ⋅ ⋅ S K S = {S_1, · · · S_K} S=S1,⋅⋅⋅SK 数量是固定的 K K K。每个平面 S i S_i Si 都通过三个平面参数 P i P_i Pi 指定。(i.e.编码法线和偏移量)我们用 D i D_i Di 来表示深度图像,它能从参数 P i P_i Pi 中推算出来。深度值的推算需要相机内置参数,而相机内置参数可以通过消隐点分析来估算。但在我们的实验中相机内置参数是通过数据集每张图像的信息提供的。
EN: Non-planar depthmap: We model non-planar structures and infer its geometry as a standard depthmap. With abuse of notation, we treat it as the ( K + 1 ) t h (K+1)^{th} (K+1)th surface and denote the depthmap as D K + 1 D_{K+1} DK+1. This does not explain planar surfaces.
CH: 非平面深度图:我们对非平面结构进行建模处理,并将它的几何结构推断为标准的深度图。用符号表示的话,我们把平面表示为 ( K + 1 ) t h (K+1)^{th} (K+1)th ,把对应的深度图表示为 D K + 1 D_{K+1} DK+1。但是这个不能用来解释平面信息。
EN: Segmentation masks: The last output is the probabilistic segmentation masks for the K K K planes ( M 1 , ⋅ ⋅ ⋅ M K ) (M_1, · · · M_K) (M1,⋅⋅⋅MK) and the non planar depthmap ( M K + 1 ) (M_{K+1}) (MK+1).
CH: 分割掩膜:最后的输出是第 K K K 个平面 ( M 1 , ⋅ ⋅ ⋅ M K ) (M_1, · · · M_K) (M1,⋅⋅⋅MK) 的分割掩膜和对应的非平面深度图 ( M K + 1 ) (M_{K+1}) (MK+1) 。
EN: In summary, the network predicts 1) plane parameters ( P 1 , ⋅ ⋅ ⋅ , P K ) (P1, ···, PK) (P1,⋅⋅⋅,PK), 2) non-planar depth maps ( D K + 1 ) (D_{K + 1}) (DK+1), and 3) probability split masks ( M 1 , ⋅ ⋅ ⋅ , M K + 1 ) (M_1, ···, M_{K + 1}) (M1,⋅⋅⋅,MK+1). We now explain more details and loss functions for each task.
CH: 概括起来,这个网络解决了三个任务:1)平面参数 ( P 1 , ⋅ ⋅ ⋅ , P K ) (P1, ···, PK) (P1,⋅⋅⋅,PK),2)非平面深度图 ( D K + 1 ) (D_{K + 1}) (DK+1),3)概率分割掩膜 ( M 1 , ⋅ ⋅ ⋅ , M K + 1 ) (M_1, ···, M_{K + 1}) (M1,⋅⋅⋅,MK+1)。下面详细说明每个任务的更多细节和损失函数。
3.1. Plane parameter branch
3.1. 平面参数分支
EN: The plane parameter branch starts with a global average pooling to reduce the feature map size to 1x1, followed by a fully connected layer to produce K × 3 K×3 K×3 plane parameters. We do not know the number of planes as well as their order in this prediction task. By following prior works, we predict a constant number ( K ) (K) (K) of planes, then allow some predictions to be invalid by letting the corresponding probabilistic segmentation masks to be 0. Our ground-truth generation process (See Sect. 4) produces at most 10 planes for most examples, thus we set K = 10 K = 10 K=10 in our experiments. We define an order-agnostic loss function based on the Chamfer distance metric for the regressed plane parameters:
L P = ∑ i = 1 K ∗ m i n j ∈ [ 1 , K ] ∥ P i ∗ − P j ∥ 2 2 L^P=\sum_{i=1}^{K^*}min_{j\in[1,K]}\Vert P_i^*-P_j \Vert_2^2 LP=i=1∑K∗minj∈[1,K]∥Pi∗−Pj∥22
The parameterization P i P_i Pi is given by the 3D coordinate of the point that is closest to the camera center on the plane. P i ∗ P^∗_i Pi∗ is the ground truth. K ∗ K^∗ K∗ is the number of ground-truth planes.
CH: 平面参数分支从一个全局平均 pooling 开始,将特征图的尺寸变成 1x1,紧接着,通过一个全连接层生成 K × 3 K×3 K×3 的平面参数。我们不知道平面的数量也不知道在这个预测任务中的顺序。通过遵循之前的工作,我们预测的平面数量为 K K K,然后通过使对应的概率分割掩膜为 0,让一些预测的平面无效。我们的大部分真实实例都可以生成十个左右的平面,(见第四节)因此在我们的实验中设置 K = 10 K=10 K=10。我们基于倒角距离度量针对平面参数的回归定义了一个与顺序无关的损失函数: L P = ∑ i = 1 K ∗ m i n j ∈ [ 1 , K ] ∥ P i ∗ − P j ∥ 2 2 L^P=\sum_{i=1}^{K^*}min_{j\in[1,K]}\Vert P_i^*-P_j \Vert_2^2 LP=i=1∑K∗minj∈[1,K]∥Pi∗−Pj∥22参数 P i P_i Pi 是根据平面上最靠近相机中心的点的3D坐标得到的。 P i ∗ P^∗_i Pi∗ 是真实实例。 K ∗ K^∗ K∗ 是真实实例中平面的数量。
3.2. Plane segmentation branch
3.2. 平面分割分支
EN: The branch begins with a pyramid pool module followed by a convolutional layer to produce a K + 1 K + 1 K+1 channel likelihood map for planar and non-planar surfaces. We added a dense conditional random field (DCRF) module based on the fast inference algorithm proposed by Krahenbuhl and Koltun, and jointly trained the DCRF module and the previous layer with Zheng et al. We set the average number of field iterations to 5 during training and set it to 10 during the test. For simplicity, the bandwidth of the bilateral filter is fixed. We use standard softmax cross entropy loss to supervise segmentation training: L M = ∑ i = 1 K + 1 ∑ p ∈ I ( 1 ( M ∗ ( p ) = i ) l o g ( 1 − M i ( p ) ) ) L^M=\sum_{i=1}^{K+1}\sum_{p \in I}(1(M^{*(p)}=i)log(1-M_i^{(p)})) LM=i=1∑K+1p∈I∑(1(M∗(p)=i)log(1−Mi(p)))The internal summation is over the image pixels ( I ) (I) (I), where M i ( p ) M^{(p)}_i Mi(p) denotes the probability of pixel p p p belonging to the i t h i^{th} ith plane. M ∗ ( p ) M^{∗(p)} M∗(p) is the ground-truth plane-id for the pixel.
CH: 这个分支以一个金字塔池化模块开始,紧接着通过一个卷积层生成平面和非平面表面 K + 1 K+1 K+1 通道的极大似然图。我们在 Krahenbuhl 和 Koltun 提出的快速推理算法的基础上添加了一个密集条件随机场(DCRF)模块,并且和 Zheng 等人共同训练这个 DCRF 模块和先前的层。我们在训练期间设置平均场迭代为5,在测试期间设置为10.为简单起见,双边滤波器的带宽是固定的。我们用标准的 softmax 交叉熵损失函数来监督分割训练: L M = ∑ i = 1 K + 1 ∑ p ∈ I ( 1 ( M ∗ ( p ) = i ) l o g ( 1 − M i ( p ) ) ) L^M=\sum_{i=1}^{K+1}\sum_{p \in I}(1(M^{*(p)}=i)log(1-M_i^{(p)})) LM=i=1∑K+1p∈I∑(1(M∗(p)=i)log(1−Mi(p)))当 M i ( p ) M^{(p)}_i Mi(p) 表示像素 p p p 属于平面 i t h i^{th} ith 的概率时,里面的求和是对图像像素 ( I ) (I) (I) 的求和。 M ∗ ( p ) M^{∗(p)} M∗(p) 是像素在真实实例上所属的平面 id。
3.3. Non-planar depth branch
3.3. 非平面深度分支
EN: The branch shares the same pyramid pooling module, followed by a convolution layer to produce a 1-channel depthmap. Instead of defining a loss specifically for non-planar regions, we found that exploiting the entire ground-truth depthmap makes the overall training more effective. Specifically, we define the loss as the sum of squared depth differences between the ground-truth and either a predicted plane or a non-planar depthmap, weighted by probabilities: L D = ∑ i = 1 K + 1 ∑ p ∈ I ( M i ( p ) ( D i ( p ) − D ∗ ( p ) ) 2 ) L^D=\sum_{i=1}^{K+1}\sum_{p\in I}(M_i^{(p)}(D_i^{(p)}-D^{*(p)})^2) LD=i=1∑K+1p∈I∑(Mi(p)(Di(p)−D∗(p))2) D i ( p ) D_i^{(p)} Di(p) denotes the depth value at pixel p, while D ∗ ( p ) D^{*(p)} D∗(p) is the ground truth depth value.
CH: 这个分支与平面分割分支分享使用同一个金字塔池化模块,然后通过一个卷积层生成1通道的深度图。我们发现使用全部的真实实例深度图来进行训练比单独定义一个非平面区域的损失要更有效。因此,我们将损失定义为真实实例与预测平面或非平面深度图之间深度差的平方和,并由概率进行加权: L D = ∑ i = 1 K + 1 ∑ p ∈ I ( M i ( p ) ( D i ( p ) − D ∗ ( p ) ) 2 ) L^D=\sum_{i=1}^{K+1}\sum_{p\in I}(M_i^{(p)}(D_i^{(p)}-D^{*(p)})^2) LD=i=1∑K+1p∈I∑(Mi(p)(Di(p)−D∗(p))2)当 D ∗ ( p ) D^{*(p)} D∗(p) 表示真实实例的深度值时, D i ( p ) D_i^{(p)} Di(p) 表示在像素 p p p 的深度值。
4. Datasets and implemenation details
4. 数据集和网络实现细节
EN: We have generated 51,000 ground-truth piece-wise planar depthmaps (50,000 training and 1,000 testing) from ScanNet, a large-scale indoor RGB-D video database. A depthmap in a single RGB-D frame contains holes and the quality deteriorates at far distances. Our approach for ground-truth generation is to directly fit planes to a consolidated mesh and project them back to individual frames, while also exploiting the associated semantic annotations.
CH: 我们从 ScanNet(一个大型室内的 RGB-D 视频数据库)中生成了 51,000 张分段平面深度图作为真实样本(50,000张训练,1,000张预测)。单幅RGB-D图像的深度图包含 holes,而且图像内容距离比较远的效果也会变坏。我们生成真实实例的方法是将平面拟合到统一的网格中,并将他们投射回单个图像帧,同时还利用了相关的语义注释。
EN: Specifically, for each sub mesh-models of the same semantic label, we treat mesh-vertices as points and repeat extracting planes by RANSAC with replacement. The inlier distance threshold is 5 c m 5cm 5cm, and the process continues until 90% of the points are covered. We merge two (not necessarily adjacent) planes that span different semantic labels if the plane normal difference is below 2 0 ◦ 20^◦ 20◦ , and if the larger plane fits the smaller one with the mean distance error below 5 c m 5cm 5cm. We project each triangle to individual frames if the three vertices are fitted by the same plane. After projecting all the triangles, we keep only the planes whose projected area is larger than 1% of an image. We discard entire frames if the ratio of pixels covered by the planes is below 50%. For training samples, we randomly choose 90% of the scenes from ScanNet, subsample every 10 frames, compute piecewise planar depthmaps with the above procedure, then use the final random sampling to produce 50,000 examples. The same procedure generates 1,000 testing examples from the remaining 10% of the scenes.
CH: 明确来说,对于相同语义标签的每个子网格模型,我们将网格顶点视为 points,并通过 RANSAC 算法重复提取平面。这个内部距离的阈值为 5 c m 5cm 5cm,并且这个过程会持续到 points 的百分之九十被覆盖。如果两个跨越不同语义标签的平面的平面法线差异小于 2 0 ◦ 20^◦ 20◦ 并且大平面拟合小平面时平均距离误差小于 5 c m 5cm 5cm,就合并这两个平面。(不一定相邻)如果三个网格顶点拟合同一个平面,就把三个顶点投射到单独的坐标系中。投射完所有的顶点,只保留投射区域大于原图面积百分之一的平面。如果所有的平面像素覆盖比小于百分之五十,就丢弃所有的平面。我们从 ScanNet 中随机选取百分之九十的场景,每十帧采样一次,使用上述流程生成分段平面深度图,然后用随机采样选出50,000个样本作为训练集。相同的流程从 ScanNet 剩余的百分之十场景中选出1,000个样本作为测试集。
EN: We have implemented PlaneNet using TensorFlow based on DeepLab . Our system is a 101-layer ResNet with Dilated Convolution, while we have followed a prior work and modified the first few layers to deal with the degridding issue. The final feature map of the DRN contains 2096 channels. We use the Adam optimizer with the initial learning rate set to 0.0003. The input image, the output plane segmentation masks, and the non-planar depthmap have a resolution of 256x192. We train our network for 50 epochs on the 50,000 training samples.
CH: 我们基于 DeepLab 的 TensorFlow 实现了 PlaneNet 。我们的方法是有着 Dilated Convolution(扩张卷积)的 101层 Resnet,我们复现了先前的工作,并修改了前几层,为了处理 degridding 的问题。最后输出的 DRN 特征图包括 2096 个通道。我们使用 Adam 优化器设置学习率为 0.0003 来进行网络训练优化。输入图像,输出的平面分割掩膜和非平面深度图的尺寸都为 256x192。我们在 50,000 个训练样本上训练了 50 轮我们的网络。
5. Experimental results
5. 实验结果
EN: Figure 3 shows the reconstruction results for various scenarios. Our end-to-end learning framework has successfully restored segmented planar and semantically meaningful structures from a single RGB image, such as a floor, wall, desktop or computer screen. We have included more examples in the supplements. We now provide a quantitative assessment of the accuracy of planar segmentation and depth reconstruction for competitive baselines, and then analyze our results more.
CH: 图三展示了各种场景的平面重建结果。我们的端到端的学习架构成功的从单幅RGB图像中重建了分段的平面结构和有意义的语义结构,比如:地板,墙面,桌面或电脑屏幕。在补充材料里有更多的实例结果。我们提出了一个针对平面分割和深度图重建的定量评估标准,然后对我们的结果进行更多的分析。

EN: Figure 3: Piece-wise planar depthmap reconstruction results by PlaneNet. From left to right: input image, plane segmentation, depthmap reconstruction, and 3D rendering of our depthmap. In the plane segmentation results, the black color shows non-planar surface regions.
CH: 图三:PlaneNet 的分段平面深度图重建结果。从左到右:输入图像,平面分割结果,深度图重建结果和深度图的3D渲染结果。在平面分割结果中,黑色显示非平面表面区域。
5.1. Plane segmentation accuracy
5.1. 平面分割准确率
EN: Piece-wise planar reconstruction from a single RGB image is a challenging problem. While existing approaches have produced encouraging results, they are based on hand-crafted features and algorithmic designs, and may not match against big-data and deep neural network (DNN) based systems. Much better baselines would then be piece-wise planar depthmap reconstruction techniques from 3D points, where input 3D points are either given by the ground truth depthmaps or inferred by a state-of-the-art DNN-based system.
CH: 单幅RGB图像的分段平面重建是一个有挑战的问题。虽然现有的方法在这方面已经有了不错的结果,但它们都是基于手动设计的特征的算法,并且可能和基于大数据和深度神经网络的系统不匹配。更好的基准线将来自于3D点的分段平面深度图重建技术,输入3D点,然后将由真实实例的深度图或最先进的DNN系统推测输出。
EN: In particular, to infer depthmaps, we have used a variant of PlaneNet which only has the pixel-wise depthmap branch, while following Eigen et al. to change the loss. Table 1 shows that this network, PlaneNet (Depth rep.), outperforms the current top-performers on the NYU benchmark.
CH: 特别是,为了推算深度图,我们使用了 PlaneNet 的变种网络,只保留像素级的深度图分支,然后参考 Eigen 等人的思想去改变损失函数。图一显示 PlaneNet 在 NYU 的基准上是目前最佳的网络。
EN: For piece-wise planar depthmap reconstruction, we have used the following three baselines from the literature.
“NYU-Toolbox” is a plane extraction algorithm from the official NYU toolbox that extracts plane hypotheses using RANSAC, and optimizes the plane segmentation via a Markov Random Field (MRF) optimization.
Manhattan World Stereo (MWS) is very similar to NYU-Toolbox except that MWS employs the Manhattan World assumption in extracting planes and exploits vanishing lines in the pairwise terms to improve results.
Piecewise Planar Stereo (PPS) relaxes the Manhattan World assumption of MWS, and uses vanishing lines to generate better plane proposals. Please see the supplementary document for more algorithmic details on the baselines.
CH: 为了对比分段平面深度图重建,我们使用了文献中的三个方法作为比较基准。
NYU-Toolbox 是 NYU 官方工具箱中的平面提取算法,使用了 RANSAC 算法提取平面候选区域,然后通过马尔可夫随机场(MRF)来优化平面分割。
Manhattan World Stereo (MWS) 与 NYU-Toolbox 很相似,不同之处在于 MWS 在提取平面时用了曼哈顿世界的假设(Manhattan World assumption),并且用成对项中的消失线来改善结果。
Piecewise Planar Stereo (PPS) 放宽了曼哈顿世界假设(Manhattan World assumption)对 MWS 的影响,并使用消失线来生成更好的平面候选区域。
EN: Figure 4 shows the evaluation results on two recall metrics. The first metric is the percentage of correctly predicted ground-truth planes. We consider a ground-truth plane being correctly predicted, if one of the inferred planes has 1) more than 0.5 Intersection over Union (IOU) score and 2) the mean depth difference over the overlapping region is less than a threshold. We vary this threshold from 0 to 0.6m with an increment of 0.05m to plot graphs. The second recall metric is simply the percentage of pixels that are in such overlapping regions where planes are correctly predicted. The figure shows that PlaneNet is significantly better than all the competing methods when inferred depthmaps are used. PlaneNet is even better than some competing methods that use ground-truth depthmaps. This demonstrates the effectiveness of our approach, learning to infer piece-wise planar structures from many examples.
CH: 图四显示了两个召回指标的评估结果。第一个指标是正确预测的真实实例平面的百分比。我们判断一个真实实例平面预测是否正确的标准是:1)是否有IOU分数大于0.5的平面,2)重叠区域的平均深度差是否小于阈值。我们让这个阈值从0 - 0.6m以0.05m的速度递增来画图。第二个指标是正确预测平面中重叠区域所占的像素百分比。该图显示,在推算深度图指标中 PlaneNet 要优于其他的方法。证明了我们的方法的有效性,从许多实例中学习推算分段平面结构。
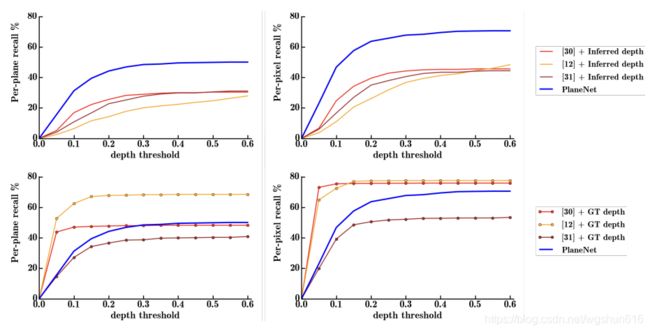
EN: Figure 4: Plane segmentation accuracy against competing baselines that use 3D points as input. Either ground-truth depthmaps or inferred depthmaps (by a DNN-based system) are used as their inputs. PlaneNet outperforms all the other methods that use inferred depthmaps. Surprisingly, PlaneNet is even better than many other methods that use ground-truth depthmaps.
CH: 图四:使用3D点作为输入,平面分割准确率的对比。或者使用真实实例深度图和基于DNN系统推算的深度图作为输入。PlaneNet 要优于其他的方法。出人意料的是,PlaneNet 比一些使用真实实例深度图的方法还要好。
EN: Figure 5 shows qualitative comparisons against existing methods with inferred depthmaps. PlaneNet produces significantly better plane segmentation results, while existing methods often generate many redundant planes where depthmaps are noisy, and fail to capture precise boundaries where the intensity edges are weak.
CH: 图五显示了与现有的方法推算出的深度图的定性比较。PlaneNet 生成了更好的平面分割结果,现有的方法会有一些冗余的平面而且深度图会有很多噪音,不能精确的捕捉到平面的边界。

EN: Figure 5: Qualitative comparisons between PlaneNet and existing methods that use inferred depthmaps as the inputs. From left to right: an input image, plane segmentation results for existing methods, and PlaneNet, respectively, and the ground-truth.
CH: 图五:使用推算的深度图作为输入,PlaneNet 与现有的其他方法的定性比较。从左往右:第一列为输入图像,第二三四列为现有其他方法的平面分割结果,第五列为PlaneNet 的平面分割结果,第六列为真实实例。
5.2. Depth reconstruction accuracy
5.2. 深度重建的准确率
EN: While the capability to infer a plane segmentation mask and precise plane parameters is the key contribution of the work, it is also interesting to compare against depth prediction methods. This is to ensure that our structured depth prediction does not compromise per-pixel depth prediction accuracy. PlaneNet makes ( K + 1 ) (K+1) (K+1) depth value predictions at each pixel. We pick the depth value with the maximum probability in the segmentation mask to define our depthmap.
CH: 虽然这个工作的关键是预测平面分割掩膜和精确的平面参数,但也能与深度预测方法进行比较。可以确保我们的深度结构化预测不会对每个像素的深度预测精度造成影响。PlaneNet 对每个像素进行了 ( K + 1 ) (K+1) (K+1) 深度值预测。我们选择分割掩膜中最大概率的深度值来定义深度图。
EN: Depth accuracies are evaluated on the NYUv2 dataset at 1) planar regions, 2) boundary regions, and 3) the entire image, against three competing baselines. Eigen-VGG is a convolutional architecture to predict both depths and surface normals. SURGE is a more recent depth inference network that optimizes planarity. FCRN is the current state-of-the-art single-image depth inference network .
CH: 深度精度评估基于 NYUv2 数据集的平面区域,边界区域和整个图像。三个对比网络分别是:Eigen-VGG 是用来预测深度值和平面法线的卷积结构。SURGE 是最新的深度推算网络可以优化平面的。FCRN 是目前最好的单图像推算网络。
EN: Depthmaps in NYUv2 are very noisy and ground-truth plane extraction does not work well. Thus, we fine-tune our network using only the depth loss. Note that the key factor in this training is that the network is trained to generate a depthmap through our piece-wise planar depthmap represen-tation. To further verify the effects of this representation, we have also fine-tuned our network in the standard per-pixel depthmap representation by disabling the plane parameter and the plane segmentation branches. In this version, denoted as “PlaneNet (Depth rep.)”, the entire depthmap is predicted in the ( K + 1 ) t h (K + 1)^{th} (K+1)th depthmap ( D K + 1 ) (D_{K+1}) (DK+1).
CH: NYUv2 的深度图有很多噪音,并且真实实例的平面提取效果不好。因此,我们只使用深度损失来 fine-tune 我们的网络。注意,训练时候的关键因素是网络经过训练可以通过我们分段平面深度信息表示生成深度图。为了进一步验证这种表示的效果,我们禁用了平面参数和平面分割掩膜两个分支,只 fine-tune 像素的深度图网络分支,这个版本表示为 PlaneNet (Depth rep.)。
EN: Table 1 shows the depth prediction accuracy on various metrics introduced in the prior work. The left five metrics provide different error statistics such as relative difference (Rel) or rooted-mean-square-error (RMSE) on the average per-pixel depth errors. The right three metrics provide the ratio of pixels, for which the relative difference between the predicted and the ground-truth depths is below a threshold. The table demonstrates that PlaneNet outperforms the state of-the-art of single-image depth inference techniques. As observed in prior works, the planarity constraint makes differences in the depth prediction task, and the improvements are more significant when our piece-wise planar representation is enforced by our network.
CH: 表一展示了先前工作中用的各种指标的深度预测准确度。左边五个是不同的误差统计,比如:平均像素深度误差的相对偏差(Rel)和均方根误差(RMSE)右边三个是像素所占的比例,对于那些预测的和实际的深度相对误差小于阈值的。该表表明 PlaneNet 要优于目前单图像深度信息推算的最新方法。之前的工作中有观察到,在深度预测任务中,平面约束可以产生积极的影响,当我们的网络强制性执行分段平面表示时,这种影响更加的明显了。

5.3. Plane ordering consistency
5.3. 平面顺序的一致性
EN: For segment depth map inference, sorting ambiguity is a challenge. We found that PlaneNet automatically learns consistent sorting without supervision, for example, the floor is always returned to the second plane. In Figure 3, the colors in the planar segmentation results are defined by the order of the planes in the network output. While ordering loses consistency for small objects or extreme camera angles, in most cases, major common surfaces such as floors and walls have a consistent ordering.
CH: 对于分割深度图的推算,平面的顺序是一个挑战。我们发现 PlaneNet 在没有干预的情况下会自动进行平面排序,例如:识别出来的地板总是被分到第二个平面。图三中,平面分割结果的颜色就由输出的平面顺序决定的。一般情况下,对于墙面,地板这些大的平面,顺序是一致的,只有在一些小平面上会失去一致性。
EN: We have taken advantage of this property and implemented a simple room layout estimation algorithm. More specifically, we look at the reconstruction example and manually select the plane entries that correspond to the ceiling, floor, and left/middle/right walls. For each possible room layout configuration (for example, a configuration with floor, left and middle walls visible), we build a 3D concave shell based on the plane parameters and project it back into the image to generate the room-layout. We measure the configured score by the number of pixels, where the constructed room layout is consistent with the inferred plane segmentation (determined by the winner). We chose the constructed room layout with the best score as our prediction. Figure 6 shows that our algorithm can generate reasonable room layout estimates even if the scene is confusing and contains many occlusion objects. Table 2 shows a quantitative assessment of the NYUv2 303 data set, where our method is comparable to the prior art designed specifically for this task.
CH: 根据这样一个特点,我们实现了一个房间布局估计算法,具体来说,我们在重建的实例中手动选择对应的天花板,墙面,地板等平面。对于每个可能的房间布局配置,我们都根据推算的平面参数构建一个3D结构,然后将这个3D结构投影到原图像生成房间的布局配置。在构建的房间布局和推断的平面分割一致时,我们通过像素的数量来衡量预测布局的效果。最后选择具有最佳效果的房间布局作为输出的预测结果。图六显示即使场景很复杂,有许多遮挡对象,我们的算法也能够生成合理的房间布局。表二显示在 NYUv2 303 数据集上,我们的方法与专门针对此任务的方法效果相当。

EN: Figure 6: Room layout estimations. We have exploited the ordering consistency in the predicted planes to infer room layouts.
CH: 图六:房间布局估计。我们利用预测平面的顺序一致性来预测房间布局。

EN: Table 2: Room layout estimations. Quantitative evaluations against the top-performers over the NYUv2 303 dataset.
CH: 表二:房间布局估计。在 NYUv2 303 数据集上与其他算法的定性效果比较。
5.4. Failure modes
5.4. 不足之处
EN: While achieving promising results on most images, PlaneNet has some failure modes as shown in Fig. 7. In the first example, PlaneNet generates two nearly co-planar vertical surfaces in the low-light region below the sink. In the second example, it cannot distinguish a white object on the floor from a white wall. In the third example, it misses a column structure on a wall due to the presence of object clutter. While the capability to infer precise plane parameters is already super-human, there is a lot of room for improvement on the planar segmentation, especially in the absence of texture information or at the presence of clutter.
CH: 虽然在很多图像上有不错的效果,但是 PlaneNet 还是有许多不足之处,如图七所示。在第一个例子中,PlaneNet 在一个低光区域产生了两个几乎共面的垂直表面,第二个例子中,没有把白色墙壁和白色物体区分开来,第三个例子中,由于杂乱物体的影响,错过了墙上的列结构。虽然 PlaneNet 在推算平面参数的能力已经时很优秀了,但是在平面分割精度方面还有待提升,尤其是在没有纹理和有杂物的情况下。

EN: Figure 7: Typical failure modes occur in the absence of enough image texture cues or at the presence of small objects and clutter.
CH: 图七:不足之处在于缺乏纹理或者有小物体遮挡的情况下。
6. Applications
6. 应用
EN: Structured geometry reconstruction is important for many application in Augmented Reality. We demonstrate two image editing pplications enabled by our piece-wise planar representation: texture insertion and replacement (see Fig. 8). We first extract Manhattan directions by using the predicted plane normals through a standard voting scheme . Given a piece-wise planar region, we define an axis of its UV coordinate by the Manhattan direction that is the most parallel to the plane, while the other axis is simply the cross product of the first axis and the plane normal. Given a UV coordinate, we insert a new texture by alpha-blending or completely replace a texture with a new one. Please see the supplementary material and the video for more AR application examples.
CH: 结构化几何重建对于增强现实中的许多应用都非常重要。通过使用我们的分段平面表示:纹理插入和替换,做了两个图像编辑的应用。(见图八)我们首先用一个标准的表决方法通过预测的平面法线来提取曼哈顿方向。给定分段平面分割的区域,我们通过最平行与平面的曼哈顿方向来定义它的 UV 坐标轴,另一个轴是第一个轴和其平面法线的叉乘。给定 UV 坐标轴,我们通过 alpha-blending 插入新的纹理或者完全替换旧纹理。更多实例请参阅补充材料及视频。

EN: Figure 8: Texture editing applications. From top to bottom, an input image, a plane segmentation result, and an edited image.
CH: 图八:图片纹理编辑应用。
7. Conclusion and future work
7. 结论及未来的工作
EN: This paper proposes PlaneNet, the first deep neural architecture for piece-wise planar depthmap reconstruction from a single RGB image. PlaneNet learns to directly infer a set of plane parameters and their probabilistic segmentation masks. The proposed approach significantly outperforms competing baselines in the plane segmentation task. It also advances the state-of-the-art in the single image depth prediction task. An interesting future direction is to go beyond the depthmap framework and tackle structured geometry prediction problems in a full 3D space.
CH: 本论文提出了第一个用于单幅图像重建分段平面深度图的深度神经网络-PlaneNet。PlaneNet 直接推断平面参数及其分割掩膜。这个方法不仅在此任务中明显的优于目前的其他方法,还推动了单一图像深度预测任务的发展。在未来一个有趣的方向是超越深度图,直接在3D空间处理几何结构化预测问题。
个人网站:心安便是归处
GitHub:oh,ss
