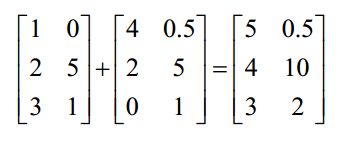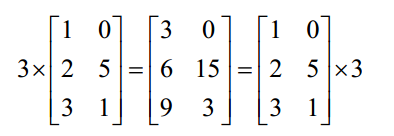吴恩达机器学习课程笔记+代码实现(3)线性代数回顾(Linear Algebra Review)
3.线性代数回顾(Linear Algebra Review)
文章目录
- 3.线性代数回顾(Linear Algebra Review)
-
-
- 3.1 矩阵和向量
- 3.2 加法和标量乘法
- 3.3 矩阵向量乘法
- 3.4 矩阵乘法
- 3.5 矩阵乘法的性质
- 3.6 逆、转置
-
如需系统学习有关机器的数学基础知识(高数、线性代数、概率论与数理统计),参见 CSDN博客链接。
3.1 矩阵和向量
如图:这个是4×2矩阵,即4行2列,如 m m m为行, n n n为列,那么 m × n m×n m×n即4×2
矩阵的维数即行数×列数
矩阵元素(矩阵项): A = [ 1402 191 1371 821 949 1437 147 1448 ] A=\left[ \begin{matrix} 1402 & 191 \\ 1371 & 821 \\ 949 & 1437 \\ 147 & 1448 \\\end{matrix} \right] A=⎣⎢⎢⎡1402137194914719182114371448⎦⎥⎥⎤
A i j A_{ij} Aij指第 i i i行,第 j j j列的元素。
向量是一种特殊的矩阵,讲义中的向量一般都是列向量,如:
y = [ 460 232 315 178 ] y=\left[ \begin{matrix} {460} \\ {232} \\ {315} \\ {178} \\\end{matrix} \right] y=⎣⎢⎢⎡460232315178⎦⎥⎥⎤
为四维列向量(4×1)。
如下图为1索引向量和0索引向量,左图为1索引向量,右图为0索引向量,一般我们用1索引向量。
y = [ y 1 y 2 y 3 y 4 ] y=\left[ \begin{matrix} { {y}_{1}} \\ { {y}_{2}} \\ { {y}_{3}} \\ { {y}_{4}} \\\end{matrix} \right] y=⎣⎢⎢⎡y1y2y3y4⎦⎥⎥⎤, y = [ y 0 y 1 y 2 y 3 ] y=\left[ \begin{matrix} { {y}_{0}} \\ { {y}_{1}} \\ { {y}_{2}} \\ { {y}_{3}} \\\end{matrix} \right] y=⎣⎢⎢⎡y0y1y2y3⎦⎥⎥⎤
3.2 加法和标量乘法
矩阵的加法:行列数相等的可以加。
3.3 矩阵向量乘法
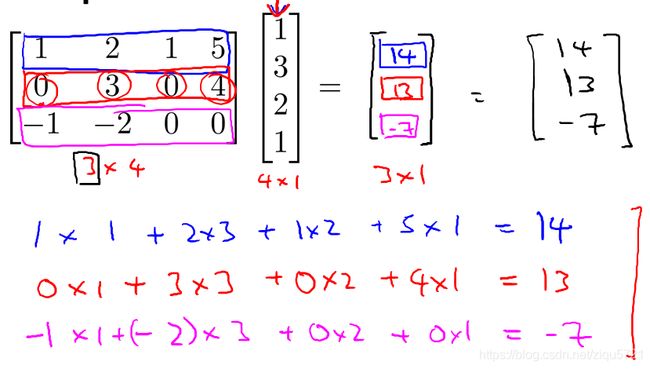
矩阵和向量的乘法如图: m × n m×n m×n的矩阵乘以 n × 1 n×1 n×1的向量,得到的是 m × 1 m×1 m×1的向量
3.4 矩阵乘法
矩阵乘法:
m × n m×n m×n矩阵乘以 n × o n×o n×o矩阵,变成 m × o m×o m×o矩阵。
如果这样说不好理解的话就举一个例子来说明一下,比如说现在有两个矩阵 A A A和 B B B,那么它们的乘积就可以表示为图中所示的形式。
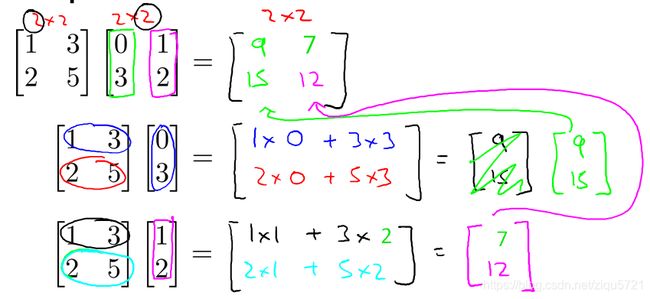
3.5 矩阵乘法的性质
矩阵乘法的性质:
矩阵的乘法不满足交换律: A × B ≠ B × A A×B≠B×A A×B̸=B×A
矩阵的乘法满足结合律。即: A × ( B × C ) = ( A × B ) × C A×(B×C)=(A×B)×C A×(B×C)=(A×B)×C
单位矩阵:在矩阵的乘法中,有一种矩阵起着特殊的作用,如同数的乘法中的1,我们称这种矩阵为单位矩阵.它是个方阵,一般用 I I I 或者 E E E 表示,本讲义都用 I I I 代表单位矩阵,从左上角到右下角的对角线(称为主对角线)上的元素均为1以外全都为0。如:
A A − 1 = A − 1 A = I A{ {A}^{-1}}={ {A}^{-1}}A=I AA−1=A−1A=I
对于单位矩阵,有 A I = I A = A AI=IA=A AI=IA=A
3.6 逆、转置
矩阵的逆:如矩阵 A A A是一个 m × m m×m m×m矩阵(方阵),如果有逆矩阵,则: A A − 1 = A − 1 A = I A{ {A}^{-1}}={ {A}^{-1}}A=I AA−1=A−1A=I
矩阵的转置:设 A A A为 m × n m×n m×n阶矩阵(即 m m m行 n n n列),第 i i i行 j j j列的元素是 a ( i , j ) a(i,j) a(i,j),即: A = a ( i , j ) A=a(i,j) A=a(i,j)
定义 A A A的转置为这样一个 n × m n×m n×m阶矩阵 B B B,满足 B = a ( j , i ) B=a(j,i) B=a(j,i),即 b ( i , j ) = a ( j , i ) b (i,j)=a(j,i) b(i,j)=a(j,i)( B B B的第 i i i行第 j j j列元素是 A A A的第 j j j行第 i i i列元素),记 A T = B { {A}^{T}}=B AT=B。(有些书记为A’=B)
直观来看,将 A A A的所有元素绕着一条从第1行第1列元素出发的右下方45度的射线作镜面反转,即得到 A A A的转置。
例:
∣ a b c d e f ∣ T = ∣ a c e b d f ∣ { {\left| \begin{matrix} a& b \\ c& d \\ e& f \\\end{matrix} \right|}^{T}}=\left|\begin{matrix} a& c & e \\ b& d & f \\\end{matrix} \right| ∣∣∣∣∣∣acebdf∣∣∣∣∣∣T=∣∣∣∣abcdef∣∣∣∣
矩阵的转置基本性质:
( A ± B ) T = A T ± B T { {\left( A\pm B \right)}^{T}}={ {A}^{T}}\pm { {B}^{T}} (A±B)T=AT±BT
( A × B ) T = B T × A T { {\left( A\times B \right)}^{T}}={ {B}^{T}}\times { {A}^{T}} (A×B)T=BT×AT
( A T ) T = A { {\left( { {A}^{T}} \right)}^{T}}=A (AT)T=A
( K A ) T = K A T { {\left( KA \right)}^{T}}=K{ {A}^{T}} (KA)T=KAT
参考资料: 吴恩达机器学习课程;黄海广机器学习课程笔记