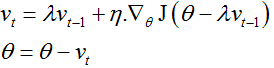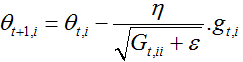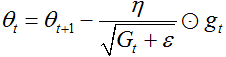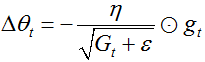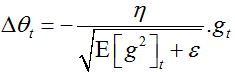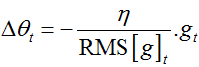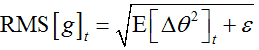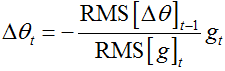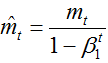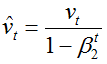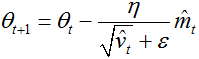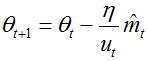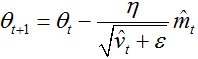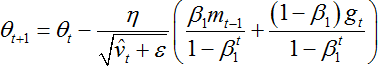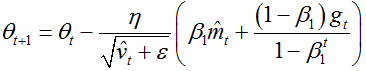秋招斩获所有互联网大厂面经之算法

背熟，唯手熟尔，大家都这么厉害，只能记得更准才行。

算法岗分类面经答案

○ 问项目
○ 机器学习：softmax, kmeans, xgboost, 随机森林，逻辑回归，SVM，l1/l2 正则化，最大似然估计，GBDT, 朴素贝叶斯，非线性分类，决策树，lightGBM, 特征选择，
○ 深度学习：unet, cnn, gan, 梯度消失，批量归一化 BN，adam，attention，损失函数，卷积，dropout，LSTM，交叉验证，SGD, sigmoid, tanh, relu, 半监督，优化器，过拟合、
○ 数学题：各种概率计算（某件事情发生的概率，数学期望，贝叶斯公式，二项分布，独立重复试验）
○ 算法题：90%都是网上的原题，二叉树、旋转数组、二分、链表、DFS, 动态规划（很少，而且都是原题）
○ 操作系统：多线程通信，用户态内核态，进程线程的区别，
○ 计算机网络：没有问到的
○ python：GIL, 多线程，dict 原理，动态数组原理，
○ c++：虚函数、虚继承、拓扑排序

问项目

① 自我介绍

自己写一个2分钟左右的自我介绍。分第一部分、第二部分、第三部分等。

② 问项目

• 针对项目内容展开，让面试官了解你的项目，将自己的做法和启发点。
• 项目中哪个地方最难，是怎样解决的，算法有什么改进的地方，怎么部署的
• 你的职业规划是怎样的？更偏向工程还是算法呢？

③ 反问

机器学习

1、softmax 反向传播的公式，需要手写

https://blog.csdn.net/Charel_CHEN/article/details/81266575

Softmax函数形式为：
$$f\left(x_i\right)=\frac{e^{x_i}}{{\sum }_{j=1}^K{e}^{x_j}}$$
现在我们对Softmax函数进行求导，分为两种情况：

(1) 当 k = i 时，
$$\frac{\partial f}{\partial x_k}=\frac{\partial f}{\partial x_i}=\frac{e^{x_i}\times {\sum }_{j=1}^K{e}^{x_j}-e^{2x_i}}{{\left({\sum }_{j=1}^K{e}^{x_j}\right)}^2}=\frac{e^{x_i}\times \left({\sum }_{j=1}^K{e}^{x_j}-e^{x_i}\right)}{{\left({\sum }_{j=1}^K{e}^{x_j}\right)}^2}=\frac{e^{x_i}}{{\sum }_{j=1}^K{e}^{x_j}}\times \frac{{\sum }_{j=1}^K{e}^{x_j}-e^{x_i}}{{\sum }_{j=1}^K{e}^{x_j}}$$
简化为：
$$\frac{\partial f}{\partial x_k}=f\left(x_k\right)\left(1-f\left(x_k\right)\right)$$
(2) 当 $k\ne i$ 时，
$$\frac{\partial f}{\partial x_k}=\frac{-e^{x_i}\times e^{x_k}}{{\left({\sum }_{j=1}^K{e}^{x_j}\right)}^2}=-f\left(x_i\right)f\left(x_k\right)$$
两者合并为：
$$\frac{\partial f}{\partial x_k}=-\sum _{i\ne k}f\left(x_i\right)f\left(x_k\right)+f\left(x_k\right)\left(1-f\left(x_k\right)\right)=f\left(x_k\right)-\sum _{i=1}^{K}f\left(x_k\right)f\left(x_i\right)$$

2、softmax 层节点过多的话有什么办法可以解决

https://www.zhihu.com/question/314486754/answer/637078850

核心思想是每块卡只负责一小部分的类别计算，每台节点只需要同步特征、特征梯度与softmax分母之和，这对于整个模型的权重和梯度来说，同步量是很微小的，基本可以忽略。通过实验，在一个八卡服务器上面，分一百万类是没有一点问题的。

1.分类类别这么大，肯定不适合用one-hot编码了，这种编码方式维度太高了。可以试试用二进制编码，然后用sigmoid分类，这种方式可以大大降低分类维度；

2.如果类别label是一段很长的文字描述，恭喜，可以试试应用分词的方法，结合word2vec词嵌入编码方式分类，类似于自然语言处理的方法；

3.分层分类，先分大类，大类中再分小类，类似于yolo9000中的树型结构的识别方法；

4.应用metric learning的方法，类似于人脸识别的方法计算类别之间的距离，实现样本之间的距离计算从而实现分类。

3、kmeans 的原理

① 原理

K-Means是典型的聚类算法，K-Means算法中的k表示的是聚类为k个簇，means代表取每一个聚类中数据值的均值作为该簇的中心，或者称为质心，即用每一个的类的质心对该簇进行描述。

② 步骤

1. 创建k个点作为起始质心。
2. 计算每一个数据点到k个质心的距离。把这个点归到距离最近的哪个质心。
3. 根据每个质心所聚集的点，重新更新质心的位置。
4. 重复2，3，直到前后两次质心的位置的变化小于一个阈值。

③ K值的确定

1. 首先一个具体的问题肯定有它的具体的业务场景，K值需要根据业务场景来定义。
2. 如果业务场景无法确定K值，我们也有技术手段来找一个合适的K。这个方法就是手肘法。

④ K-Means与KNN

K-Means是无监督学习的聚类算法，没有样本输出；而KNN是监督学习的分类算法，有对应的类别输出。KNN基本不需要训练，对测试集里面的点，只需要找到在训练集中最近的k个点，用这最近的k个点的类别来决定测试点的类别。而K-Means则有明显的训练过程，找到k个类别的最佳质心，从而决定样本的簇类别。

当然，两者也有一些相似点，两个算法都包含一个过程，即找出和某一个点最近的点。两者都利用了最近邻(nearest neighbors)的思想。

4、kmeans 为什么一定会收敛

https://blog.csdn.net/sunnyxidian/article/details/89630927

https://www.bbsmax.com/A/gVdnKNGEzW/

• 收敛条件：直到前后两次质心的位置的变化小于一个阈值，最终这个变化会逐渐减小。

• 可以从优化目标的角度看，K-Means优化的目标是每个样本离其所属类中心点的距离平方和，在每一步迭代过程中分为两个步骤：更新中心点以及更新样本的所属类。这两个步骤都会使目标函数减小。因此一定会收敛。也可以把K-Means看做EM算法的特例，EM算法是可以保证收敛的。

• kmeans过程收敛是因为 他的数据划分判断bai依据 欧式距离 与 均值算质心 这两步搭配du
  恰好是EM算法的特例，EM算法的收敛性非常复杂，解释不清楚。

5、CART了解吗？怎么做回归和分类的？

https://www.cnblogs.com/en-heng/p/5035945.html

https://www.cnblogs.com/keye/p/10564914.html

分类与回归树（Classification and Regression Trees, CART）是由四人帮Leo Breiman, Jerome Friedman, Richard Olshen与Charles Stone于1984年提出，既可用于分类也可用于回归。

分类树流程

CART分类树建立算法流程，之所以加上建立，是因为CART分类树算法有剪枝算法流程。

算法输入训练集D，基尼系数的阈值，样本个数阈值。

输出的是决策树T。

算法从根节点开始，用训练集递归建立CART分类树。

(1)、对于当前节点的数据集为D，如果样本个数小于阈值或没有特征，则返回决策子树，当前节点停止递归。

(2)、计算样本集D的基尼系数，如果基尼系数小于阈值，则返回决策树子树，当前节点停止递归。

(3)、计算当前节点现有的各个特征的各个特征值对数据集D的基尼系数，对于离散值和连续值的处理方法和基尼系数的计算见第二节。缺失值的处理方法和C4.5算法里描述的相同。

(4)、在计算出来的各个特征的各个特征值对数据集D的基尼系数中，选择基尼系数最小的特征A和对应的特征值a。根据这个最优特征和最优特征值，把数据集划分成两部分D1和D2，同时建立当前节点的左右节点，做节点的数据集D为D1，右节点的数据集D为D2。

(5)、对左右的子节点递归的调用1-4步，生成决策树。

对生成的决策树做预测的时候，假如测试集里的样本A落到了某个叶子节点，而节点里有多个训练样本。则对于A的类别预测采用的是这个叶子节点里概率最大的类别。

回归树流程

CART回归树和CART分类树的建立类似，这里只说不同。

(1)、分类树与回归树的区别在样本的输出，如果样本输出是离散值，这是分类树；样本输出是连续值，这是回归树。分类树的输出是样本的类别，回归树的输出是一个实数。

(2)、连续值的处理方法不同。

(3)、决策树建立后做预测的方式不同。

分类模型：采用基尼系数的大小度量特征各个划分点的优劣。

回归模型：采用和方差度量，度量目标是对于划分特征A，对应划分点s两边的数据集D1和D2，求出使D1和D2各自集合的均方差最小，同时D1和D2的均方差之和最小。

​ 对于决策树建立后做预测的方式，CART分类树采用叶子节点里概率最大的类别作为当前节点的预测类别。回归树输出不是类别，采用叶子节点的均值或者中位数来预测输出结果。

6、huber函数了解吗？和l1、l2比起来优势是啥？

L1范数损失函数，也被称为最小绝对值偏差（LAD），最小绝对值误差（LAE）
$$S=\sum _{i=1}^n\left|Y_i-f\left(x_i\right)\right|$$

L2范数损失函数，也被称为最小平方误差（LSE）
$$S=\sum _{i=1}^n{\left(Y_i-f\left(x_i\right)\right)}^2$$

l1和l2都存在的问题：若数据中90%的样本对应的目标值为150，剩下10%在0到30之间。

那么使用MAE作为损失函数的模型可能会忽视10%的异常点，而对所有样本的预测值都为150，因为模型会按中位数来预测；MSE的模型则会给出很多介于0到30的预测值，因为模型会向异常点偏移。

Huber损失，平滑的平均绝对误差：本质上，Huber损失是绝对误差，只是在误差很小时，就变为平方误差。误差降到多小时变为二次误差由超参数δ（delta）来控制。当Huber损失在[0-δ,0+δ]之间时，等价为MSE，而在[-∞,δ]和[δ,+∞]时为MAE。
$$L_{\delta }(y,f(x))=\{\begin{array}{ll}\frac{1}{2}(y-f(x){)}^2& \text{ for }|y-f(x)|\le \delta \\ \delta |y-f(x)|-\frac{1}{2}{\delta }^2& \text{ otherwise }\end{array}$$
优点：Huber损失结合了MSE和MAE的优点，对异常点更加鲁棒。

8、机器学习中一般怎么衡量模型效果？auc值怎么理解？

https://blog.csdn.net/i96jie/article/details/82781803

1、混淆矩阵

TP(True Positive): 真实为1类，预测也为1类

FN(False Negative): 真实不为1类，预测为1类

FP(False Positive): 真实为1类，预测不为1类

TN(True Negative): 真实不为1类，预测也不为1类

2、准确率和召回率
$$\begin{gathered} Precision=\frac{TP}{TP+FP} \\ Recall=\frac{TP}{TP+FN} \end{gathered}$$
3、F值(F-Measure)

F-Measure是Precision和Recall加权调和平均
KaTeX parse error: Can't use function '$' in math mode at position 2: $̲F=\frac{\left(a…
a是参数，当a=1是，即为最常见F1.

4、ROC和AUC

ROC

受试者工作特征曲线 （receiver operating characteristic curve，简称ROC曲线），又称为感受性曲线（sensitivity curve）。
$$\begin{gathered} \text{TruePositiveRate}(TPR)=\frac{TP}{TP+FN} \\ \text{FalsePositiveRate}(FPR)=\frac{FP}{FP+TN} \end{gathered}$$

在ROC 空间中，每个点的横坐标是FPR，纵坐标是TPR。根据不同的阈值进行分类，根据分类结果计算得到ROC空间中相应的点，连接这些点就形成ROC curve。

AUC

AUC (Area Under Curve) 被定义为ROC曲线下的面积，显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围一般在0.5和1之间。

AUC更大的分类器效果更好

9、怎么衡量两个分布的差异？KL散度和交叉熵损失有什么不同？关系是啥？

https://blog.csdn.net/Avery123123/article/details/102681688

衡量两个分布的差异的指标

KL散度、JS散度、交叉熵和Wasserstein距离

KL散度（Kullback–Leibler divergence）：

KL散度又称为相对熵，信息散度，信息增益。
$$D_{KL}(P\Vert Q)=-\sum _{x\in X}P(x)\log \frac{1}{P(x)}+\sum _{x\in X}P(x)\log \frac{1}{Q(x)}=\sum _{x\in X}P(x)\log \frac{P(x)}{Q(x)}$$
JS散度（Jensen-Shannon divergence）:

JS散度度量两个概率分布的相似度，基于KL散度的变体，解决了KL散度非对称的问题。
$$JS\left(P_1\Vert P_2\right)=\frac{1}{2}KL\left(P_1\Vert \frac{P_1+P_2}{2}\right)+\frac{1}{2}KL\left(P_2\Vert \frac{P_1+P_2}{2}\right)$$
交叉熵（Cross Entropy）:

在神经网络中，交叉熵可以作为损失函数，因为它可以衡量P和Q的相似性。
$$\mathrm{H}(\mathrm{P},\mathrm{Q})=\sum P(x)\log \frac{1}{Q(x)}$$
Wasserstein距离:

真实数据与生成数据的概率分布距离
$$W\left(P_r,P_g\right)=\underset{\gamma \sim \Pi \left(P_r,P_g\right)}{\inf }{\mathbb{E}}_{(x,y)\sim \gamma }[\Vert x-y\Vert ]$$
KL散度和交叉熵损失的区别与联系

https://blog.csdn.net/Dby_freedom/article/details/83374650

一句话总结的话：KL散度可以被用于计算代价，而在特定情况下最小化KL散度等价于最小化交叉熵。而交叉熵的运算更简单，所以用交叉熵来当做代价。

KL散度和交叉熵在特定条件下等价

https://www.cnblogs.com/jiangnanyanyuchen/p/12148246.html
$$\begin{array}{c}{D}_{KL}(p\Vert q)={\sum }_{i=1}^{n}p\left(x_i\right)\log \left(\frac{p\left(x_i\right)}{q\left(x_i\right)}\right)\\ ={\sum }_{i=1}^{n}p\left(x_i\right)\log \left(p\left(x_i\right)\right)-{\sum }_{i=1}^{n}p\left(x_i\right)\log \left(q\left(x_i\right)\right)\\ =-H(p(x))+\left[-{\sum }_{i=1}^{n}p\left(x_i\right)\log \left(q\left(x_i\right)\right)\right]\end{array}$$
前者$H(p(x))$表示信息熵，后者为交叉熵，KL 散度 = 交叉熵- 信息熵。

10、怎么理解最大似然估计？

https://zhuanlan.zhihu.com/p/26614750

极大似然估计，通俗理解来说，就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！

换句话说，极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。

11、逻辑斯蒂回归里面，输出的那个0-1之间的值，是概率值吗？你看它又叫对数几率回归，怎么理解几率这个概念？

是不是概率值

https://blog.csdn.net/euzmin/article/details/104538328

一般情况下不是，如果y服从伯努利分布且η与x满足线性关系，则确实是在对概率进行建模。

这两个假设并不是那么容易满足的。所以，很多情况下，我们得出的逻辑回归输出值，无法当作真实的概率，只能作为置信度来使用。

怎么理解几率

https://blog.csdn.net/hustwayne/article/details/82781875

没找到答案

12、比较下随机森林和GBDT

https://blog.csdn.net/login_sonata/article/details/73929426

1. 随机森林采用的bagging思想，而GBDT采用的boosting思想。这两种方法都是Bootstrap思想的应用，Bootstrap是一种有放回的抽样方法思想。虽然都是有放回的抽样，但二者的区别在于：Bagging采用有放回的均匀取样，而Boosting根据错误率来取样（Boosting初始化时对每一个训练样例赋相等的权重1／n，然后用该算法对训练集训练t轮，每次训练后，对训练失败的样例赋以较大的权重），因此Boosting的分类精度要优于Bagging。Bagging的训练集的选择是随机的，各训练集之间相互独立，弱分类器可并行，而Boosting的训练集的选择与前一轮的学习结果有关，是串行的。
2. 组成随机森林的树可以是分类树，也可以是回归树；而GBDT只能由回归树组成。
3. 组成随机森林的树可以并行生成；而GBDT只能是串行生成。
4. 对于最终的输出结果而言，随机森林采用多数投票等；而GBDT则是将所有结果累加起来，或者加权累加起来。
5. 随机森林对异常值不敏感；GBDT对异常值非常敏感。
6. 随机森林对训练集一视同仁；GBDT是基于权值的弱分类器的集成。
7. 随机森林是通过减少模型方差提高性能；GBDT是通过减少模型偏差提高性能。

13、随机森林的随机怎么理解？

https://blog.csdn.net/login_sonata/article/details/73929426

随机森林的随机性主要体现在两个方面：

1. 数据集的随机选取：从原始的数据集中采取有放回的抽样（bagging），构造子数据集，子数据集的数据量是和原始数据集相同的。不同子数据集的元素可以重复，同一个子数据集中的元素也可以重复。
2. 待选特征的随机选取：与数据集的随机选取类似，随机森林中的子树的每一个分裂过程并未用到所有的待选特征，而是从所有的待选特征中随机选取一定的特征，之后再在随机选取的特征中选取最优的特征。

以上两个随机性能够使得随机森林中的决策树都能够彼此不同，提升系统的多样性，从而提升分类性能。

14、SVM 公式、思想

思想

https://blog.csdn.net/CSDN_Black/article/details/79446504

距离超平面最小的样例，我们称之为支持向量，我们所要找的最优超平面，就是使支持向量到超平面距离最大，我们认为，这样的超平面，就是最优的，下面也是要想办法求出这个超平面。SVM的核心问题就是找到这一超平面。

公式

https://www.cnblogs.com/hello-ai/p/11332654.html

我们将SVM转换为带有条件约束的最优化问题:
$$\{\begin{array}{l}{\min }_w\frac{1}{2}\Vert w{\Vert }^2\\ y_i\left(w^T{x}_i+b\right)\ge 1\end{array}$$
还有很多公式，需要看一下中间过程，这个只是最终过程。

15、特征选择有哪些方法

http://www.mianshigee.com/question/11579ztq/

特征选择一般有三种方式，过滤式、包裹式和嵌入式，过滤式常见的是深度学习中利用卷积核进行特征提取，整个训练过程是先进行特征提取，然后才开始学习，包裹式是将最终学习器的性能作为特征子集的评价准则，不断通过更新候选子集，然后利用交叉验证更新特征，计算量比较大，嵌入式是将特征选择和训练过程融为一体，在训练过程中自动进行了特征选择，例如L1正则，产生稀疏特征

https://blog.csdn.net/coffee_cream/article/details/61423223

过滤式选择: 如 Relief

过滤式方法先对数据集进行特征选择，然后再训练学习器，特征选择过程与后续学习器无关。
　　Relief（Relevant FeaturesRelevant Features）是著名的过滤式特征选择方法，Relief 为一系列算法，它包括最早提出的 Relief 以及后来拓展的 Relief-F 和 RRelief-F ，其中最早提出的 Relief 针对的是二分类问题，RRelief-F 算法可以解决多分类问题，RRelief-F算法针对的是目标属性为连续值的回归问题。

包裹式选择: 如 LVW（Las Vegas Wrapper）

包裹式选择直接把最终将要使用的学习器的性能作为特征子集的评价依据，也就是说，包裹式特征选择是为给定的学习器选择最有利的特征子集。

嵌入式选择：如基于 L1L1 正则化的学习方法就是一种嵌入式的特征选择方法

嵌入式选择是将特征选择过程与学习器训练过程融合为一体，两者在同一个优化过程中完成，即在学习器训练过程中自动地进行了特征选择。

16、GBDT的原理，和随机森林等算法做比较

https://blog.csdn.net/kwame211/article/details/81671048

GBDT （Gradient Boost Decision Tree 梯度提升决策树） 原理

① **概念：**GBDT是以决策树为基学习器的迭代算法，注意GBDT里的决策树都是回归树而不是分类树。Boost是”提升”的意思，一般Boosting算法都是一个迭代的过程，每一次新的训练都是为了改进上一次的结果。
② 核心：GBDT的核心就在于：每一棵树学的是之前所有树结论和的残差，这个残差就是一个加预测值后能得真实值的累加量。比如A的真实年龄是18岁，但第一棵树的预测年龄是12岁，差了6岁，即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习，如果第二棵树真的能把A分到6岁的叶子节点，那累加两棵树的结论就是A的真实年龄；如果第二棵树的结论是5岁，则A仍然存在1岁的残差，第三棵树里A的年龄就变成1岁，继续学习。
③ 优点：GBDT优点是适用面广，离散或连续的数据都可以处理，几乎可用于所有回归问题（线性/非线性），亦可用于二分类问题（设定阈值，大于阈值为正例，反之为负例）。缺点是由于弱分类器的串行依赖，导致难以并行训练数据。

和随机森林等算法做比较

上面有个已经说了

17、svm损失函数推导

https://www.zhihu.com/question/62881491?sort=created

通常来讲SVM是为了找到具有最大间隔的超平面，而这个最大间隔由 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pFqSRI9W-1604755233981)(https://www.zhihu.com/equation?tex=%5Cfrac%7B1%7D%7B%7C%7Cw%7C%7C%7D)] 决定，而所有样本点是需要满足一个约束条件 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YGRZFdfa-1604755233985)(https://www.zhihu.com/equation?tex=y_i%28w%5ETx_i%2Bb%29%5Cgeq1)] 的，这是一个有约束的优化问题，因而优化目标 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-L4fUPfTr-1604755233996)(https://www.zhihu.com/equation?tex=max%5Cfrac%7B1%7D%7B%7C%7Cw%7C%7C%7D)] 适用于对偶+拉格朗日乘数法来解决。

当我们允许有某些错误样本出现的时候，就需要考虑到希望有尽量少的不满足约束的点，因而为这些“坏点”定义一个惩罚项，优化目标就可以转变为 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SVQ8V0jB-1604755234006)(https://www.zhihu.com/equation?tex=min%5Cfrac%7B1%7D%7B2%7D%7C%7Cw%7C%7C%5E2%2BC%5Csum+l_%7B0%2F1%7D%28y_i%28w%5ETx_i%2Bb%29-1%29)] 。如果把后面的这个惩罚项换成 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uZ0KPlx0-1604755234034)(https://www.zhihu.com/equation?tex=max%280%2C+1-y_i%28w%5ETx_i%2Bb%29%29)]就变成了经典形式的SVM。

从另外的角度来看是指将模型最后的预测值与ground truth的误差当作优化目标，我们需要学习出参数 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HFOPGooH-1604755234040)(https://www.zhihu.com/equation?tex=w)], [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7wpjWJPE-1604755234050)(https://www.zhihu.com/equation?tex=b)]使得误差最小。

例如在二分类SVM中，我们希望当样本点满足 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ihtFiPIT-1604755234056)(https://www.zhihu.com/equation?tex=w%5ETx_i%2Bb%5Cgeq0)] 时，预测 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-m9KsVu9E-1604755234060)(https://www.zhihu.com/equation?tex=y%3D%2B1)]，而 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SCQZ3eBq-1604755234067)(https://www.zhihu.com/equation?tex=w%5ETx_i%2Bb%5Cleq0)]时，我们预测 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JlfDZkOx-1604755234083)(https://www.zhihu.com/equation?tex=y_i%3D-1)]，但是这样还不太可靠，如果我们想提高模型预测的置信度，我们可以定义一个margin [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-evuGJfyK-1604755234086)(https://www.zhihu.com/equation?tex=%5CDelta)] ,使得 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SZmWTDIo-1604755234110)(https://www.zhihu.com/equation?tex=w%5ETx_i%2Bb%5Cgeq%5CDelta)] 时判断 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0oicCWz0-1604755234111)(https://www.zhihu.com/equation?tex=y%3D%2B1)]（负例同理，因而联立起来变为 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-va0dSxYi-1604755234112)(https://www.zhihu.com/equation?tex=y_i%28w%5ETx_i%2Bb%29%5Cgeq%5CDelta)]），当样本点没有满足这个条件的时候，就会有损失，合理的方式就是使用hinge loss损失函数 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VN5FZRLz-1604755234115)(https://www.zhihu.com/equation?tex=max%280%2C+%5CDelta-y_i%28w%5ETx_i%2Bb%29%29)]，而这时问题就变为了一个无约束的优化问题。

而为了使模型泛化性能更好，我们加上正则项 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LBYDhD99-1604755234119)(https://www.zhihu.com/equation?tex=%5Cfrac%7BC%7D%7B2%7D%7C%7Cw%7C%7C%5E2)] ，损失函数就变成了 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vIXLd4fg-1604755234128)(https://www.zhihu.com/equation?tex=%5Csum+max%280%2C1-y_i%28w%5ETx_i%2Bb%29%29%2B%5Cfrac%7BC%7D%7B2%7D%7C%7Cw%7C%7C%5E2)] ，这时可以看出从这种角度出发得到目标函数和和前面相同了，而且这种情况下使用简单的梯度下降就可以进行优化。

18、朴素贝叶斯写公式。

http://www.360doc.com/content/19/0704/12/60116915_846649701.shtml
$$\mathrm{P}\left(C_k\mid x\right)=\frac{P\left(C_k\right){\prod }_{i=1}^{n}P\left(x_i\mid C_k\right)}{{\sum }_{k=1}^k\left[P\left(C_k\right){\prod }_{i=1}^{n}P\left(x_i\mid C_k\right)\right]}$$

19、介绍一下xgboost有哪些特点

https://blog.csdn.net/qq_35290785/article/details/97564676

1. 正则化项防止过拟合
2. xgboost不仅使用到了一阶导数，还使用二阶导数，损失更精确，还可以自定义损失
3. XGBoost的并行优化，XGBoost的并行是在特征粒度上的
4. 考虑了训练数据为稀疏值的情况，可以为缺失值或者指定的值指定分支的默认方向，这能大大提升算法的效率
5. 支持列抽样，不仅能降低过拟合，还能减少计算

20、xgboost和GBDT的分裂方式你认为哪个好

xgboost 好：

https://www.cnblogs.com/jiangxinyang/p/9248154.html

① 传统的贪心算法效率较低，修改boost 实现了一种近似贪心算法，用来加速和减小内存消耗，除此之外还考虑了稀疏数据集和缺失值的处理，对于特征的值有缺失的样本，XGBoost依然能自动找到其要分裂的方向。

② 在进行节点分裂时，计算每个特征的增益，最终选择增益最大的那个特征去做分割，那么各个特征的增益计算就可以开多线程进行。

21、设计能适应测试集里有缺失值的训练集没有的GBDT， 要求不能从填充数据的角度来做

https://blog.csdn.net/zhaomengszu/article/details/80775554

没看懂

22、LSTM减弱梯度消失的原理

总结：

LSTM把原本RNN的单元改造成一个叫做CEC的部件，这个部件保证了误差将以常数的形式在网络中流动 ，并在此基础上添加输入门和输出门使得模型变成非线性的，并可以调整不同时序的输出对模型后续动作的影响。

分析：

RNN产生梯度消失与梯度爆炸的原因就在于 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OJVPV6p2-1604755234131)(https://www.zhihu.com/equation?tex=%5Cprod_%7Bj%3Dk%2B1%7D%5Et+%5Cfrac%7B%5Cdelta+S_j%7D%7B%5Cdelta+S_%7Bj-1%7D%7D+)] ， 如果我们能够将这一坨东西去掉， 我们的不就解决掉梯度问题了吗。 LSTM通过门机制来解决了这个问题。

通俗地讲

RNN中，每个记忆单元h_t-1都会乘上一个W和激活函数的导数，这种连乘使得记忆衰减的很快，而LSTM是通过记忆和当前输入"相加"，使得之前的记忆会继续存在而不是受到乘法的影响而部分“消失”，因此不会衰减。但是这种naive的做法太直白了，实际上就是个线性模型，在学习效果上不够好，因此LSTM引入了那3个门：遗忘门、输入门、输出门。

23、介绍方向导数和梯度，方向导数和梯度的关系？为什么梯度在机器学习中的优化方法中有效？

https://www.zhihu.com/question/36301367

梯度是向量，方向导数是数量。梯度是各个偏导数组成的一个向量，方向导数是各个偏导数与方向余弦相乘再求和。梯度这个方向的方向导数是最大的。

方向导数

顾名思义，方向导数就是某个方向上的导数。是一个数量。

梯度

是一个矢量，其方向上的方向导数最大，其大小正好是此最大方向导数。

方向导数与梯度的关系

• 方向导数是各个方向上的导数
• 偏导数连续才有梯度存在
• 梯度的方向是方向导数中取到最大值的方向，梯度的值是方向导数的最大值

为什么梯度在机器学习中的优化方法中有效？

因为我们在山上的时候是不知道山的具体形状的，因此无法找到一条全局最优路线。那我们只能关注脚下的路，将每一步走好，这就是梯度下降法的原理。

https://blog.csdn.net/jingyi130705008/article/details/78851722

梯度下降的更新公式为：
$$\begin{array}{l}{\theta }_0={\theta }_0-\alpha \frac{\partial J}{\partial {\theta }_0}\\ {\theta }_1={\theta }_1-\alpha \frac{\partial J}{\partial {\theta }_1}\end{array}$$
其中，∂J/∂θ表示的就是当前位置下坡最快的方向，而α（learning rate）则表示前行一步的步长为多大。从图中，我们可以看到代价函数J有很多个局部最低点，因此梯度下降的最大特点就是求得的解仅是局部最优解。

24、贝叶斯公式在机器学习里有哪些应用

用于参数估计。机器学习做的事情其实就是找到一个概率分布函数，输入一个数据输出是这个数据属于某个类的概率。
那么怎么找这个概率分布函数呢？一般是默认是高斯分布。

25、说一下支持向量机，贝叶斯，树模型，实用性、局限性

https://blog.csdn.net/m0_37676632/article/details/73440857

https://www.cnblogs.com/daliner/p/9887639.html

支持向量机

优点：

可以解决高维问题，即大型特征空间；

能够处理非线性特征的相互作用；

无需依赖整个数据；

可以提高泛化能力；

缺点：

当观测样本很多时，效率并不是很高；

对非线性问题没有通用解决方案，有时候很难找到一个合适的核函数；

对缺失数据敏感；

贝叶斯

朴素贝叶斯（NB）属于生成式模型（即需要计算特征与类的联合概率分布），计算过程非常简单，只是做了一堆计数。NB有一个条件独立性假设，即在类已知的条件下，各个特征之间的分布是独立的。这样朴素贝叶斯分类器的收敛速度将快于判别模型，如逻辑回归，所以只需要较少的训练数据即可。即使NB条件独立假设不成立，NB分类器在实践中仍然表现的很出色。它的主要缺点是它不能学习特征间的相互作用，用mRMR中的R来讲，就是特征冗余。

优点：

朴素贝叶斯模型发源于古典数学理论，有着坚实的数学基础，以及稳定的分类效率。

对小规模的数据表现良好，能处理多分类任务，适合增量式训练。

对缺失数据不太敏感，算法也比较简单，常用于文本分类（如垃圾邮件过滤）

缺点：

需要计算先验概率

​ 分类决策存在错误率

对输入数据的表达形式很敏感。

树模型

优点：

​ 计算简单，易于理解，可解释性强；

​ 比较适合处理有缺失属性的样本；

​ 能够处理不相关的特征；

​ 在相对短的时间内能够对大型数据源做出可行且效果良好的结果。

缺点：

​ 容易发生过拟合（随机森林可以很大程度上减少过拟合）；

​ 忽略了数据之间的相关性；

​ 对于那些各类别样本数量不一致的数据，在决策树当中,信息增益的结果偏向于那些具有更多数值的特征（只要是使用了信息增 益，都有这个缺点，如RF）。

26、计算样本熵的公式方法，假设检验

样本熵：https://blog.csdn.net/u011389706/article/details/80984209

假设检验：https://zhuanlan.zhihu.com/p/86178674

27、机器学习流程

https://blog.csdn.net/qq_27567859/article/details/79666969

1. 数据源：

机器学习的第一个步骤就是收集数据，这一步非常重要，因为收集到的数据的质量和数量将直接决定预测模型是否能够建好。我们可以将收集的数据去重复、标准化、错误修正等等，保存成数据库文件或者csv格式文件，为下一步数据的加载做准备。

2. 分析：

这一步骤主要是数据发现，比如找出每列的最大、最小值、平均值、方差、中位数、三分位数、四分位数、某些特定值（比如零值）所占比例或者分布规律等等都要有一个大致的了解。了解这些最好的办法就是可视化，谷歌的开源项目facets可以很方便的实现。另一方面要确定自变量(x1…xn)和因变量y，找出因变量和自变量的相关性，确定相关系数。

3. 特征选择：

特征的好坏很大程度上决定了分类器的效果。将上一步骤确定的自变量进行筛选，筛选可以手工选择或者模型选择，选择合适的特征，然后对变量进行命名以便更好的标记。命名文件要存下来，在预测阶段的时候会用到。

4. 向量化：

向量化是对特征提取结果的再加工，目的是增强特征的表示能力，防止模型过于复杂和学习困难，比如对连续的特征值进行离散化，label值映射成枚举值，用数字进行标识。这一阶段将产生一个很重要的文件：label和枚举值对应关系，在预测阶段的同样会用到。

5. 拆分数据集：

需要将数据分为两部分。用于训练模型的第一部分将是数据集的大部分。第二部分将用于评估我们训练有素的模型的表现。通常以8:2或者7:3进行数据划分。不能直接使用训练数据来进行评估，因为模型只能记住“问题”。

6. 训练：

进行模型训练之前，要确定合适的算法，比如线性回归、决策树、随机森林、逻辑回归、梯度提升、SVM等等。选择算法的时候最佳方法是测试各种不同的算法，然后通过交叉验证选择最好的一个。但是，如果只是为问题寻找一个“足够好”的算法，或者一个起点，也是有一些还不错的一般准则的，比如如果训练集很小，那么高偏差/低方差分类器（如朴素贝叶斯分类器）要优于低偏差/高方差分类器（如k近邻分类器），因为后者容易过拟合。然而，随着训练集的增大，低偏差/高方差分类器将开始胜出（它们具有较低的渐近误差），因为高偏差分类器不足以提供准确的模型。

7. 评估：

训练完成之后，通过拆分出来的训练的数据来对模型进行评估，通过真实数据和预测数据进行对比，来判定模型的好坏。模型评估的常见的五个方法：混淆矩阵、提升图&洛伦兹图、基尼系数、ks曲线、roc曲线。混淆矩阵不能作为评估模型的唯一标准，混淆矩阵是算模型其他指标的基础。

8. 文件整理：

模型训练完之后，要整理出四类文件，确保模型能够正确运行，四类文件分别为：Model文件、Lable编码文件、元数据文件（算法，参数和结果）、变量文件（自变量名称列表、因变量名称列表）。

9. 接口封装：

通过封装封装服务接口，实现对模型的调用，以便返回预测结果。

10. 上线：

28、H0和H1能否互换

https://www.zhihu.com/question/24168200

H0和H1并不是不能互换，但是选取的H0原则是H0必须是一个可以被拒绝的假设。对于一个假设检验问题，如果H1是一个不能被拒绝的假设，那么H0和H1不能互换。

什么样的H1是不能被拒绝的假设？比如下面这个问题：总体是一个班级的所有同学一次的考试成绩，原假设H0是全班同学的平均成绩为80分，H1是全班同学的平均成绩不是80分。在这个框架中，H0是一个可以被拒绝的假设，H1是一个不能被拒绝的假设。为什么这么说？如果H0选做全班同学的平均成绩不是80分，那么哪怕你知道全班几乎所有人的成绩，不妨认为平均是80分，只要有一个人的成绩你不知道，那么知道其他人的成绩对于你拒绝H0没有任何帮助。只有在这个人恰好80分的情况下，原假设是不成立的，这个人是81或者79,原假设都成立。从另一个角度，也可以认为当H0是一个不能被拒绝的假设的时候，H0太过宽泛，和H1区分不了。

在H1是一个可以被拒绝的假设的时候，H0和H1可以互换。比如H0是全班成绩小于80分，H1是全班成绩大于80分，这种情况H0和H1可以互换，但是需要注意的是互换之后假设检验的目标就变化了。

29、L1、L2 正则化

① 概念

L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓“惩罚”是指对损失函数中的某些参数做一些限制
L1正则化是指权值向量w中各个元素的绝对值之和
L2正则化是指权值向量w中各个元素的平方和然后求平方根

② 作用

L1、L2都是对损失函数的优化，L范式都是为了防止模型过拟合，所谓范式就是加入参数的约束。
L1的作用是为了矩阵稀疏化。假设的是模型的参数取值满足拉普拉斯分布。
L2的作用是为了使模型更平滑，得到更好的泛化能力。假设的是参数是满足高斯分布

③ 区别

L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择
L2正则化可以防止模型过拟合；一定程度上，L1也可以防止过拟合

④ 为什么正则化能降低过拟合

降低过拟合程度：正则化之所以能够降低过拟合的原因在于，正则化是结构风险最小化的一种策略实现。给loss function加上正则化项，能使得新得到的优化目标函数h = f+normal，需要在f和normal中做一个权衡（trade-off），如果还像原来只优化f的情况下，那可能得到一组解比较复杂，使得正则项normal比较大，那么h就不是最优的，因此可以看出加正则项能让解更加简单，通过降低模型复杂度，得到更小的泛化误差，降低过拟合程度。
L1正则化和L2正则化：L1正则化就是在loss function后加正则项为L1范数，加上L1范数容易得到稀疏解(0比较多)。L2正则化就是loss function后加正则项为L2范数的平方，加上L2正则相比于L1正则来说，得到的解比较平滑(不时稀疏)。但是同样能够保证解中接近于0(但不是等于0，所以相对平滑)的维度比较多，降低模型的复杂度。

31、树模型中分叉的判断有哪些：信息增益，信息增益比，Gini系数；他们有什么区别

https://www.cnblogs.com/muzixi/p/6566803.html

有哪些

信息增益，信息增益比，Gini系数

信息增益 （ID3算法 ）

定义： 以某特征划分数据集前后的熵的差值。

**做法：**计算使用所有特征划分数据集D，得到多个特征划分数据集D的信息增益，从这些信息增益中选择最大的，因而当前结点的划分特征便是使信息增益最大的划分所使用的特征。

信息增益的理解：

​ 对于待划分的数据集D，其 entroy(前)是一定的，但是划分之后的熵 entroy(后)是不定的，entroy(后)越小说明使用此特征划分得到的子集的不确定性越小（也就是纯度越高），因此 entroy(前) - entroy(后)差异越大，说明使用当前特征划分数据集D的话，其纯度上升的更快。而我们在构建最优的决策树的时候总希望能更快速到达纯度更高的集合，这一点可以参考优化算法中的梯度下降算法，每一步沿着负梯度方法最小化损失函数的原因就是负梯度方向是函数值减小最快的方向。同理：在决策树构建的过程中我们总是希望集合往最快到达纯度更高的子集合方向发展，因此我们总是选择使得信息增益最大的特征来划分当前数据集D。

缺点：信息增益偏向取值较多的特征

原因：当特征的取值较多时，根据此特征划分更容易得到纯度更高的子集，因此划分之后的熵更低，由于划分前的熵是一定的，因此信息增益更大，因此信息增益比较 偏向取值较多的特征。

信息增益比（C4.5算法）

信息增益比 = 惩罚参数 * 信息增益

信息增益比本质： 是在信息增益的基础之上乘上一个惩罚参数。特征个数较多时，惩罚参数较小；特征个数较少时，惩罚参数较大。

缺点：信息增益比偏向取值较少的特征

原因： 当特征取值较少时HA(D)的值较小，因此其倒数较大，因而信息增益比较大。因而偏向取值较少的特征。

**使用信息增益比：基于以上缺点，**并不是直接选择信息增益率最大的特征，而是现在候选特征中找出信息增益高于平均水平的特征，然后在这些特征中再选择信息增益率最高的特征。

Gini系数（CART算法 —分类树）

**定义：**基尼指数（基尼不纯度）：表示在样本集合中一个随机选中的样本被分错的概率。

注意： Gini指数越小表示集合中被选中的样本被分错的概率越小，也就是说集合的纯度越高，反之，集合越不纯。

即 基尼指数（基尼不纯度）= 样本被选中的概率 * 样本被分错的概率

区别：

https://www.zhihu.com/question/263901789

1、ID3相比C4.5的劣势，即信息增益相对信息增益比的劣势，是信息增益容易偏向取值较多的特征，三个概率相等的取值就比两个概率相等的取值的信息增益要大。采用信息增益比可以校正这一问题；
2、C4.5相比CART分类树的劣势，即信息增益比相对gini系数的劣势，是熵的计算用到了大量的对数运算，计算机中对数运算相对于基本运算需要的时间成本更多，这在模型较为复杂时会严重拖慢计算速度。所以采用gini系数作为判断标准可以在保证准确率的同时加快计算速度。
其他的比如CART是二叉树所以效率更高，或者CART可以进行回归之类的和本题关系不大就不说了。
总之CART是一种更为成熟的决策树算法，应用范围更广。当然现在提升树更加流行了。

32、LightGBM和xgboost的区别

https://www.cnblogs.com/mata123/p/7440774.html

1. xgboost采用的是level-wise的分裂策略，而lightGBM采用了leaf-wise的策略，区别是xgboost对每一层所有节点做无差别分裂，可能有些节点的增益非常小，对结果影响不大，但是xgboost也进行了分裂，带来了务必要的开销。 leaft-wise的做法是在当前所有叶子节点中选择分裂收益最大的节点进行分裂，如此递归进行，很明显leaf-wise这种做法容易过拟合，因为容易陷入比较高的深度中，因此需要对最大深度做限制，从而避免过拟合。
2. **lightgbm使用了基于histogram的决策树算法，这一点不同与xgboost中的 exact 算法，histogram算法在内存和计算代价上都有不小优势。
   -. 内存上优势：很明显，直方图算法的内存消耗为(#data #features * 1Bytes)(因为对特征分桶后只需保存特征离散化之后的值)，而xgboost的exact算法内存消耗为：(2 * #data * #features 4Bytes)，因为xgboost既要保存原始feature的值，也要保存这个值的顺序索引，这些值需要32位的浮点数来保存。
   -. 计算上的优势，预排序算法在选择好分裂特征计算分裂收益时需要遍历所有样本的特征值，时间为(#data),而直方图算法只需要遍历桶就行了，时间为(#bin)
3. LightGBM 支持直方图做差加速
   -. 一个子节点的直方图可以通过父节点的直方图减去兄弟节点的直方图得到，从而加速计算。
4. lightgbm支持直接输入categorical 的feature
   -. 在对离散特征分裂时，每个取值都当作一个桶，分裂时的增益算的是”是否属于某个category“的gain。类似于one-hot编码。
5. 但实际上xgboost的近似直方图算法也类似于lightgbm这里的直方图算法，为什么xgboost的近似算法比lightgbm还是慢很多呢？
   -. xgboost在每一层都动态构建直方图， 因为xgboost的直方图算法不是针对某个特定的feature，而是所有feature共享一个直方图(每个样本的权重是二阶导),所以每一层都要重新构建直方图，而lightgbm中对每个特征都有一个直方图，所以构建一次直方图就够了。
   -. lightgbm做了cache优化？
6. lightgbm哪些方面做了并行？
   -. feature parallel
   一般的feature parallel就是对数据做垂直分割（partiion data vertically，就是对属性分割），然后将分割后的数据分散到各个workder上，各个workers计算其拥有的数据的best splits point, 之后再汇总得到全局最优分割点。但是lightgbm说这种方法通讯开销比较大，lightgbm的做法是每个worker都拥有所有数据，再分割？（没懂，既然每个worker都有所有数据了，再汇总有什么意义？这个并行体现在哪里？？）
   -. data parallel
   传统的data parallel是将对数据集进行划分，也叫 平行分割(partion data horizontally)， 分散到各个workers上之后，workers对得到的数据做直方图，汇总各个workers的直方图得到全局的直方图。 lightgbm也claim这个操作的通讯开销较大，lightgbm的做法是使用”Reduce Scatter“机制，不汇总所有直方图，只汇总不同worker的不同feature的直方图(原理？)，在这个汇总的直方图上做split，最后同步。

33、LightGBM的直方图排序后会比xgboost的效果差吗，为什么

这个不一定是这个答案

不会。

LIghtGBM的优点之一是：

更高的准确率(相比于其他任何提升算法) : 它通过leaf-wise分裂方法产生比level-wise分裂方法更复杂的树，这就是实现更高准确率的主要因素。然而，它有时候或导致过拟合，但是我们可以通过设置 max-depth 参数来防止过拟合的发生。

34、比较两个样本分布均值的差异，t检验，具体哪些指标

① t 检验概念

T检验是通过比较不同数据的均值，研究两组数据之间是否存在显著差异。

② t 检验分类

1.单样本T检验

用于比较一组数据与一个特定数值之间的差异情况。

2.配对样本的T检验

用于检验有一定对应关系的样本之间的差异情况，需要两组样本数相等。

常见的使用场景有：

①同一对象处理前后的对比（同一组人员采用同一种减肥方法前后的效果对比）；

②同一对象采用两种方法检验的结果的对比（同一组人员分别服用两种减肥药后的效果对比）；

③配对的两个对象分别接受两种处理后的结果对比（两组人员，按照体重进行配对，服用不同的减肥药，对比服药后的两组人员的体重）。

3.独立样本的T检验

独立样本与配对样本的不同之处在于独立样本T检验两组数据的样本个数可以不等。

③ t 检验的具体指标

t 值：在进行t检验时，会计算出一个t值，而在选定显著性水平后，可以找到相比较的t值，两者可以比较，判断显著性。

p值：代表的是不接受原假设的最小的显著性水平，可以与选定的显著性水平直接比较。

35、L1-norm和L2-norm的区别

1.L1是模型各个参数的绝对值之和。L2是模型各个参数的平方和的开方值。

2.L1会趋向于产生少量的特征，而其他的特征都是0.因为最优的参数值很大概率出现在坐标轴上，这样就会导致某一维的权重为0 ，产生稀疏权重矩阵。 L2会选择更多的特征，这些特征都会接近于0。 最优的参数值很小概率出现在坐标轴上，因此每一维的参数都不会是0。当最小化||w||时，就会使每一项趋近于0

36、SVM可以自己选择核函数么

https://www.zhihu.com/question/21883548

可以自己选择。

在我的工作中，最常用的是Linear核与RBF核。

1. Linear核：主要用于线性可分的情形。参数少，速度快，对于一般数据，分类效果已经很理想了。
2. RBF核：主要用于线性不可分的情形。参数多，分类结果非常依赖于参数。有很多人是通过训练数据的交叉验证来寻找合适的参数，不过这个过程比较耗时。我个人的体会是：使用libsvm，默认参数，RBF核比Linear核效果稍差。通过进行大量参数的尝试，一般能找到比linear核更好的效果。

至于到底该采用哪种核，要根据具体问题，有的数据是线性可分的，有的不可分，需要多尝试不同核不同参数。如果特征的提取的好，包含的信息量足够大，很多问题都是线性可分的。当然，如果有足够的时间去寻找RBF核参数，应该能达到更好的效果。

39、SVM的推导。还问了SVM如果不用对偶怎么做

推导过程：https://www.cnblogs.com/wumh7/p/9453582.html

SVM 的对偶：https://zhuanlan.zhihu.com/p/31131842

不用对偶：没找到答案

40、推导逻辑回归

https://blog.csdn.net/qq_38923076/article/details/82925183

https://www.jianshu.com/p/0cfabca442d9

41、推导 HMM

https://blog.csdn.net/Oscar6280868/article/details/88550586

42、为什么LSTM会优于传统的RNN？

因为LSTM有进有出且当前的cell information是通过input gate控制之后叠加的，RNN是叠乘，因此LSTM可以防止梯度消失或爆炸。

LSTM的效果：

1、当gate是关闭的，那么就会阻止对当前信息的改变，这样以前的依赖信息就会被学到。

2、当gate是打开的时候，并不是完全替换之前的信息，而是在之前信息和现在信息之间做加权平均。所以，无论网络的深度有多深，输入序列有多长，只要gate是打开的，网络都会记住这些信息。

43、LSTM怎么解决梯度消失？不同门的作用

https://www.cnblogs.com/bonelee/p/10475453.html

RNN产生梯度消失与梯度爆炸的原因就在于 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MEWrbLV7-1604755234135)(https://www.zhihu.com/equation?tex=%5Cprod_%7Bj%3Dk%2B1%7D%5Et+%5Cfrac%7B%5Cdelta+S_j%7D%7B%5Cdelta+S_%7Bj-1%7D%7D+)] ， 如果我们能够将这一坨东西去掉， 我们的不就解决掉梯度问题了吗。 LSTM通过门机制来解决了这个问题。

我们先从LSTM的三个门公式出发：

• 遗忘门： [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XNAIvNu9-1604755234137)(https://www.zhihu.com/equation?tex=f_t+%3D+%5Csigma%28+W_f+%5Ccdot+%5Bh_%7Bt-1%7D%2C+x_t%5D+%2B+b_f%29)]
• 输入门： [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SsVLwL1l-1604755234138)(https://www.zhihu.com/equation?tex=i_t+%3D+%5Csigma%28W_i+%5Ccdot+%5Bh_%7Bt-1%7D%2C+x_t%5D+%2B+b_i%29)]
• 输出门： [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PdkqEYki-1604755234140)(https://www.zhihu.com/equation?tex=o_t+%3D+%5Csigma%28W_o+%5Ccdot+%5Bh_%7Bt-1%7D%2C+x_t+%5D+%2B+b_0+%29)]

我们注意到， 首先三个门的激活函数是sigmoid， 这也就意味着这三个门的输出要么接近于0 ， 要么接近于1。这就使得 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KUnZF6N7-1604755234217)(https://www.zhihu.com/equation?tex=%5Cfrac%7B%5Cdelta+c_t%7D%7B%5Cdelta+c_%7Bt-1%7D%7D+%3D+f_t%EF%BC%8C+%5Cfrac%7B%5Cdelta+h_t%7D%7B%5Cdelta+h_%7Bt-1%7D%7D+%3D+o_t)] 是非0即1的，当门为1时， 梯度能够很好的在LSTM中传递，很大程度上减轻了梯度消失发生的概率， 当门为0时，说明上一时刻的信息对当前时刻没有影响， 我们也就没有必要传递梯度回去来更新参数了。所以， 这就是为什么通过门机制就能够解决梯度的原因： 使得单元间的传递 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MN3L3wQV-1604755234223)(https://www.zhihu.com/equation?tex=%5Cfrac%7B%5Cdelta+S_j%7D%7B%5Cdelta+S_%7Bj-1%7D%7D)] 为0 或 1。

不同门的作用：

因为LSTM对记忆的操作是相加的，线性的，使得不同时序的记忆对当前的影响相同，为了让不同时序的记忆对当前影响变得可控，LSTM引入了输入门和输出门，之后又有人对LSTM进行了扩展，引入了遗忘门。

44、GBDT的原理，怎么做多分类问题

GBDT 原理

https://www.jianshu.com/p/9b647afc1cdc

做多分类问题

本人理解：多分类变成多个二分类，比如说当前类别A，训练集的标签为属于A的为1，其他为0，该值为连续值（概率），基于这所有的样本生成一棵树；结果为对类别A的预测值f(x)；然后B标签，C标签同理可得；然后通过softmax层处理下得到属于各个类别的概率值；这里每一轮迭代都会和类别数目相同的树；每一棵树针对一个类别进行学习并输出对应的分数，然后就n个类别的分数，经过softmax层变成概率值；

45、XGBoost的基本思想，和GBDT的区别

基本思想

http://www.elecfans.com/d/995278.html

xgboost是一种集成学习算法，属于3类常用的集成方法(bagging,boosting,stacking)中的boosting算法类别。它是一个加法模型，基模型一般选择树模型，但也可以选择其它类型的模型如逻辑回归等。

区别

xgboost属于梯度提升树(GBDT)模型这个范畴，GBDT的基本想法是让新的基模型（GBDT以CART分类回归树为基模型）去拟合前面模型的偏差，从而不断将加法模型的偏差降低。相比于经典的GBDT，xgboost做了一些改进，从而在效果和性能上有明显的提升（划重点面试常考）。第一，GBDT将目标函数泰勒展开到一阶，而xgboost将目标函数泰勒展开到了二阶。保留了更多有关目标函数的信息，对提升效果有帮助。第二，GBDT是给新的基模型寻找新的拟合标签（前面加法模型的负梯度），而xgboost是给新的基模型寻找新的目标函数（目标函数关于新的基模型的二阶泰勒展开）。第三，xgboost加入了和叶子权重的L2正则化项，因而有利于模型获得更低的方差。**第四，xgboost增加了自动处理缺失值特征的策略。**通过把带缺失值样本分别划分到左子树或者右子树，比较两种方案下目标函数的优劣，从而自动对有缺失值的样本进行划分，无需对缺失特征进行填充预处理。

此外，xgboost还支持候选分位点切割，特征并行等，可以提升性能。

46、随机森林和boosting trees的区别

Bagging和Boosting 的主要区别

https://www.cnblogs.com/onemorepoint/p/9264782.html

• 样本选择上: Bagging采取Bootstraping的是随机有放回的取样，Boosting的每一轮训练的样本是固定的，改变的是买个样的权重。
• 样本权重上：Bagging采取的是均匀取样，且每个样本的权重相同，Boosting根据错误率调整样本权重，错误率越大的样本权重会变大
• 预测函数上：Bagging所以的预测函数权值相同，Boosting中误差越小的预测函数其权值越大。
• 并行计算: Bagging 的各个预测函数可以并行生成;Boosting的各个预测函数必须按照顺序迭代生成.

深度学习

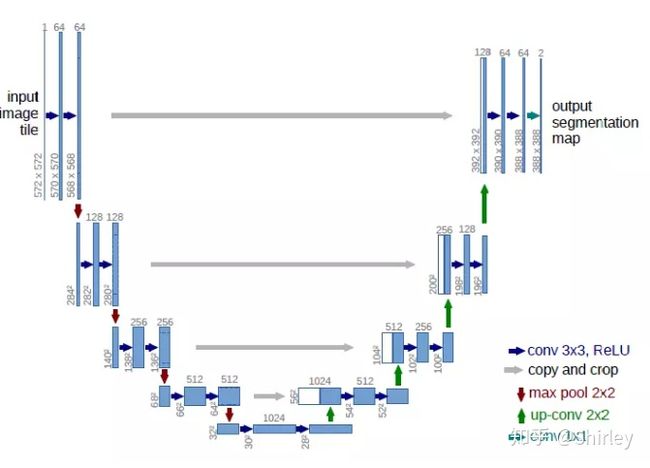
1、unet 结构，为什么要上采样、下采样

unet 结构

Unet网络的典型特点是，它是U型对称结构，左侧是卷积层，右侧是上采样层。原文的Unet结构中，包含4个convolutional layer和对应的4个up sampling layer。

先下采样后上采样的好处：

1.降低显存和计算量，图小了占内存也就小了，运算量也少了。

2.增大感受野，使同样3*3的卷积能在更大的图像范围上进行特征提取。大感受野对分割任务很重要，小感受野是做不了多类分割的，而且分割出来的掩膜边界很粗糙！！

3.多出几条不同程度下采样的分支，可以很方便进行多尺度特征的融合。多级语义融合会让分类很准。

2、了解目标检测吗，常见目标检测模型了解吗？

常见的有：Faster R-CNN、SSD和YOLO

https://blog.csdn.net/weixin_42273095/article/details/81699352

3、训练怎么监督的，损失函数是啥，你认为深度学习在其中学到了什么？

这个问题是针对自己的项目说的：有监督学习、损失函数是 dice loss，深度学习学到了是数据分布。

4、怎么解决梯度消失问题？

1. 使用 ReLU、LReLU、ELU、maxout 等激活函数
   sigmoid函数的梯度随着x的增大或减小和消失，而ReLU不会。
2. 使用批规范化
   通过规范化操作将输出信号规范化到均值为0，方差为1保证网络的稳定性.从上述分析分可以看到，反向传播式子中有的存在，所以的大小影响了梯度的消失和爆炸，Batch Normalization 就是通过对每一层的输出规范为均值和方差一致的方法，消除了带来的放大缩小的影响，进而解决梯度消失和爆炸的问题。

5、批量归一化的思想，还了解其他归一化吗？

批量归一化的思想

在数据送入神经网络的某一层进行处理之前，对数据做归一化。按照训练样本的批量进行处理，先减掉这批样本的均值，然后除以标准差，然后进行缩放和平移。缩放和平移参数同训练得到。预测时使用训练时确定的这些值来计算

其他的归一化

五种归一化

1. Batch Normalization，其论文：https://arxiv.org/pdf/1502.03167.pdf

2. Layer Normalizaiton，其论文：https://arxiv.org/pdf/1607.06450v1.pdf

3. Instance Normalization，其论文：https://arxiv.org/pdf/1607.08022.pdf

4. Group Normalization，其论文：https://arxiv.org/pdf/1803.08494.pdf

5. Switchable Normalization，其论文：https://arxiv.org/pdf/1806.10779.pdf

Batch Normalization：

1.BN的计算就是把每个通道的NHW单独拿出来归一化处理

2.针对每个channel我们都有一组γ,β，所以可学习的参数为2*C

3.当batch size越小，BN的表现效果也越不好，因为计算过程中所得到的均值和方差不能代表全局

Layer Normalizaiton：

1.LN的计算就是把每个CHW单独拿出来归一化处理，不受batchsize 的影响

2.常用在RNN网络，但如果输入的特征区别很大，那么就不建议使用它做归一化处理

Instance Normalization

1.IN的计算就是把每个HW单独拿出来归一化处理，不受通道和batchsize 的影响

2.常用在风格化迁移，但如果特征图可以用到通道之间的相关性，那么就不建议使用它做归一化处理

Group Normalizatio

1.GN的计算就是把先把通道C分成G组，然后把每个gHW单独拿出来归一化处理，最后把G组归一化之后的数据合并成CHW

2.GN介于LN和IN之间，当然可以说LN和IN就是GN的特列，比如G的大小为1或者为C

Switchable Normalization

1.将 BN、LN、IN 结合，赋予权重，让网络自己去学习归一化层应该使用什么方法

2.集万千宠爱于一身，但训练复杂

6、说下平时用到的深度学习的trick

1：优化器。机器学习训练的目的在于更新参数，优化目标函数，常见优化器有SGD，Adagrad，Adadelta，Adam，Adamax，Nadam。其中SGD和Adam优化器是最为常用的两种优化器，SGD根据每个batch的数据计算一次局部的估计，最小化代价函数。学习速率决定了每次步进的大小，因此我们需要选择一个合适的学习速率进行调优。学习速率太大会导致不收敛，速率太小收敛速度慢。因此SGD通常训练时间更长，但是在好的初始化和学习率调度方案的情况下，结果更可靠。Adam优化器结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点，能够自动调整学习速率，收敛速度更快，在复杂网络中表现更优。

2：学习速率。学习速率的设置第一次可以设置大一点的学习率加快收敛，后续慢慢调整；也可以采用动态变化学习速率的方式（比如，每一轮乘以一个衰减系数或者根据损失的变化动态调整学习速率）。

3：dropout。数据第一次跑模型的时候可以不加dropout，后期调优的时候dropout用于防止过拟合有比较明显的效果，特别是数据量相对较小的时候。dropout的原理是使一部分神经元失效，仅仅保留一部分神经元的计算，因此添加dropout层的位置为cnn或者lstm层之后。机器学习的目标是优化方差和偏差，而过拟合是机器学习常见的问题，dropout能降低过拟合，其原因在于dropout使部分神经元失效之后，每次模型都只学到部分的特征（类似于随机深林），降低了模型了方差。

4：变量初始化。常见的变量初始化有零值初始化、随机初始化、均匀分布初始值、正态分布初始值和正交分布初始值。一般采用正态分布或均匀分布的初始化值，有的论文说正交分布的初始值能带来更好的效果。实验的时候可以才正态分布和正交分布初始值做一个尝试。

5：训练轮数。模型收敛即可停止迭代，一般可采用验证集作为停止迭代的条件。如果连续几轮模型损失都没有相应减少，则停止迭代。

6：正则化。为了防止过拟合，可通过加入l1、l2正则化。从公式可以看出，加入l1正则化的目的是为了加强权值的稀疏性，让更多值接近于零。而l2正则化则是为了减小每次权重的调整幅度，避免模型训练过程中出现较大抖动。

7：预训练。对需要训练的语料进行预训练可以加快训练速度，并且对于模型最终的效果会有少量的提升，常用的预训练工具有word2vec和glove。

8：激活函数。常用的激活函数为sigmoid、tanh、relu、leaky relu、elu。采用sigmoid激活函数计算量较大，而且sigmoid饱和区变换缓慢，求导趋近于0，导致梯度消失。sigmoid函数的输出值恒大于0，这会导致模型训练的收敛速度变慢。tanh它解决了zero-centered的输出问题，然而，gradient vanishing的问题和幂运算的问题仍然存在。relu从公式上可以看出，解决了gradient vanishing问题并且计算简单更容易优化，但是某些神经元可能永远不会被激活，导致相应的参数永远不能被更新（Dead ReLU Problem）；leaky relu有relu的所有优点，外加不会有Dead ReLU问题，但是在实际操作当中，并没有完全证明leaky relu总是好于relu。elu也是为解决relu存在的问题而提出，elu有relu的基本所有优点，但计算量稍大，并且没有完全证明elu总是好于relu。

9：特征学习函数。常用的特征学习函数有cnn、rnn、lstm、gru。cnn注重词位置上的特征，而具有时序关系的词采用rnn、lstm、gru抽取特征会更有效。gru是简化版的lstm，具有更少的参数，训练速度更快。但是对于足够的训练数据，为了追求更好的性能可以采用lstm模型。

10：特征抽取。max-pooling、avg-pooling是深度学习中最常用的特征抽取方式。max-pooling是抽取最大的信息向量，然而当存在多个有用的信息向量时，这样的操作会丢失大量有用的信息。avg-pooling是对所有信息向量求平均，当仅仅部分向量相关而大部分向量无关时，会导致有用信息向量被噪声淹没。针对这样的情况，在有多个有用向量的情形下尽量在最终的代表向量中保留这些有用的向量信息，又想在只有一个显著相关向量的情形下直接提取该向量做代表向量，避免其被噪声淹没。那么解决方案只有：加权平均，即Attention。

11：每轮训练数据乱序。每轮数据迭代保持不同的顺序，避免模型每轮都对相同的数据进行计算。

12：batch_size选择。对于小数据量的模型，可以全量训练，这样能更准确的朝着极值所在的方向更新。但是对于大数据，全量训练将会导致内存溢出，因此需要选择一个较小的batch_size。如果这时选择batch_size为1，则此时为在线学习，每次修正方向为各自样本的梯度方向修正，难以达到收敛。batch_size增大，处理相同数据量的时间减少，但是达到相同精度的轮数增多。实际中可以逐步增大batch_size，随着batch_size增大，模型达到收敛，并且训练时间最为合适。

7、说下adam的思想

Adam是在RMSProp的基础上进行改进的，该算法与RMSProp不同的是，Adam不仅对累加状态变量 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cbnFP5oG-1604755234234)(https://www.zhihu.com/equation?tex=s_t)] 进行指数加权平均，还对每一个小批量的梯度 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-skDaLn57-1604755234240)(https://www.zhihu.com/equation?tex=g_t)] 进行指数加权平均。Adam本质上实际是RMSProp+动量

8、基础的分类模型有哪些

机器学习：线性分类器（如LR)、支持向量机（SVM）、朴素贝叶斯（NB）、K近邻（KNN）、决策树（DT）、集成模型（RF/GDBT等）

深度学习：AlexNet、VGG Net、GoogleNet、ResNet

9、机器学习模型如何应用到产品上

flask 搭建网络服务、Tensorflow Serving 部署

10、L1和L2做loss的优缺点，为什么L1的做正则项时稀疏性更好

1、L1 loss 在零点不平滑，用的较少
2、Smooth L1 Loss 修改零点不平滑问题

3、L2 loss：对离群点比较敏感，如果feature 是 unbounded的话，需要好好调整学习率，防止出现梯度爆炸的情况[fast rcnn]

4、一般来说，L1正则会制造稀疏的特征，大部分无用特征的权重会被置为0。 L2正则会让特征的权重不过大，使得特征的权重比较平均。

5、L1-smooth 比 l2 loss 更加鲁棒

11、非线性分类算法有哪些

https://blog.csdn.net/m0_37922329/article/details/86175830?utm_medium=distribute.pc_relevant.none-task-blog-baidulandingword-1&spm=1001.2101.3001.4242

决策树、K近邻、集成学习（Bagging, 随机森林，Boosting: AdaBoost）、非线性 SVM、BP 神经网络

12、如何判断一个算法是线性的还是非线性的

快速判断非线性的方法：

• (变量)^n，且n不为1
• |变量| 有变量在绝对值內的为非线性
• sgn(变量) 有变量在符号函数之内

13、GAN的损失函数形式是什么样的？

https://zhuanlan.zhihu.com/p/72195907
$$\underset{G}{\min }\underset{D}{\max }V(D,G)=E_{x\sim p_{\text{data }}(x)}[\log D(x)]+E_{z\sim p_z(z)}[\log (1-D(G(z)))]$$

14、介绍一下什么是GAN？

GAN用一个生成模型和一个判别模型,判别模型用于判断给定的图片是不是真实的图片,生成模型自己生成一张图片和想要的图片很像,开始时两个模型都没有训练,然后两个模型一起进行对抗训练,生成模型产生图片去欺骗判别模型,判别模型去判别真假,最终两个模型在训练过程中,能力越来越强最终达到稳态。

15、GAN是怎么训练的？

GAN的训练模式是这样的：固定生成器G，迭代k次训练判别器D；然后固定判别器D，训练生成器G，两者依次交替使用梯度下降法进行更新。

16、输入为$L\ast L$，卷积核为$k\ast k$，还有步长s和padding p，求输出尺寸？求操作的FLOPs？

有问题，需要确认

输出尺寸：
$$N=(L-k+2p)/s+1$$
参数数量：

c: 输入通道数，n: 输出通道数，
$$参数数量=n\times (h\times w\times c+1)$$

FlOPs 计算量：
$$H^{\prime }\times W^{\prime }\times 参数数量$$

FLOPs的概念：全称是floating point operations per second，意指每秒浮点运算次数，即用来衡量硬件的计算性能；在CNN中用来指浮点运算次数；

17、过拟合要怎么解决？

Early stopping、数据集扩增、正则化

18、几个激活函数都有什么优缺点（sigmoid, tanh, relu）

https://blog.csdn.net/kuweicai/article/details/93926393

① Sigmoid

• 连续，且平滑便于求导
  但是缺点也同样明显。
• none-zero-centered（非零均值， Sigmoid 函数 的输出值恒大于0），会使训练出现 zig-zagging dynamics 现象，使得收敛速度变慢。
• 梯度消失问题。 由于Sigmoid的导数总是小于1，所以当层数多了之后，会使回传的梯度越来越小，导致梯度消失问题。而且在前向传播的过程中，通过观察Sigmoid的函数图像，当 x 的值大于2 或者小于-2时，Sigmoid函数的输出趋于平滑，会使权重和偏置更新幅度非常小，导致学习缓慢甚至停滞。
• 计算量大。由于采用了幂计算。

② tanh

优点主要是解决了none-zero-centered 的问题，但是缺点依然是梯度消失，计算消耗大。但是如果和上面的 sigmoid 激活函数相比， tanh 的导数的取值范围为(0, 1)， 而 sigmoid 的导数的取值范围为(0,1/4)，显然sigmoid 会更容易出现梯度消失，所以 tanh 的收敛速度会比 sigmoid 快。

③ relu

优点：

• x 大于0时，其导数恒为1，这样就不会存在梯度消失的问题
• 计算导数非常快，只需要判断 x 是大于0，还是小于0
• 收敛速度远远快于前面的 Sigmoid 和 Tanh函数

缺点：

• none-zero-centered
• Dead ReLU Problem，指的是某些神经元可能永远不会被激活，导致相应的参数永远不能被更新。因为当x 小于等于0时输出恒为0，如果某个神经元的输出总是满足小于等于0 的话，那么它将无法进入计算。有两个主要原因可能导致这种情况产生: (1) 非常不幸的参数初始化，这种情况比较少见 (2) learning rate太高导致在训练过程中参数更新太大，不幸使网络进入这种状态。解决方法是可以采用 MSRA 初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。

19、BN的作用

https://zhuanlan.zhihu.com/p/62309136?utm_source=wechat_session

BN的作用：

1 加速网络收敛速度

2 本质上解决反向传播中梯度消失问题

进而提升训练稳定性的效果

BN的具体操作：

通过对每一层的输出规范为均值为0，方差为1.

20、设计一个在CNN卷积核上做dropout的方式

没有找到答案

21、cross validation

方法：

将数据集平均分成N份

选其中的N-1份作为训练集（training set），剩余的1份作为验证集(validation set)

用以上N种情况的训练集训练得到模型的参数

22、对优化方法SGD、adam是否了解

https://blog.csdn.net/wydbyxr/article/details/84822806

GD

1）Batch gradient descent(批量梯度下降)
  在整个数据集上
  每更新一次权重，要遍历所有的样本，由于样本集过大，无法保存在内存中，无法线上更新模型。对于损失函数的凸曲面，可以收敛到全局最小值，对于非凸曲面，收敛到局部最小值。
  随机梯度下降（SGD）和批量梯度下降（BGD）的区别。SGD 从数据集中拿出一个样本，并计算相关的误差梯度，而批量梯度下降使用所有样本的整体误差：「关键是，在更新中没有随机或扩散性的行为。」

2）stochastic gradient descent(SGD,随机梯度下降)
  可以在线学习，收敛的更快，可以收敛到更精确的最小值。但是梯度更新太快，而且会产生梯度震荡，使收敛不稳定。
  随机梯度下降（SGD）和批量梯度下降（BGD）的区别。SGD 从数据集中拿出一个样本，并计算相关的误差梯度，而批量梯度下降使用所有样本的整体误差：「关键是，在更新中没有随机或扩散性的行为。」

3）Mini-batch gradient descent(MBGD,小批量梯度下降)
  批量梯度下降算法和随机梯度下降算法的结合体。两方面好处：一是减少更新的次数，使得收敛更稳定；二是利用矩阵优化方法更有效。
  当训练集有很多冗余时（类似的样本出现多次），batch方法收敛更快。
  以一个极端情况为例，若训练集前一半和后一半梯度相同。那么如果前一半作为一个batch，后一半作为另一个batch，那么在一次遍历训练集时，batch的方法向最优解前进两个step，而整体的方法只前进一个step。

adam

https://blog.csdn.net/bvl10101111/article/details/72616516

1.Adam算法可以看做是修正后的Momentum+RMSProp算法

2.动量直接并入梯度一阶矩估计中（指数加权）

3.Adam通常被认为对超参数的选择相当鲁棒

4.学习率建议为0.001

23、FaceNet里的triplet loss的公式，反向传播如何更新

这个是他的项目中问题，可以不看

24、又问了一次hierarchy softmax

这个是 NLP 中的，不用看

25、sigmoid, tanh, relu的区别

上面已经写了

26、半监督学习里无标签样本的打标

使用伪标签：该方法的主旨思想其实很简单。首先，在标签数据上训练模型，然后使用经过训练的模型来预测无标签数据的标签，从而创建伪标签。此外，将标签数据和新生成的伪标签数据结合起来作为新的训练数据。

27、如何调参

学习率：

• 执行学习率范围测试以确定“大”的学习率。
• 一轮测试确定最大学习速率，将最小学习速率设置为最大学习速率的十分之一。

动量：

• 用短期动量值0.99、0.97、0.95和0.9进行测试，以获得动量的最佳值；
• 如果使用周期学习率计划，最好从该最大动量值开始循环设置动量，并随着学习率的增加而减小到0.8或0.85；

批量大小：

• 根据硬件条件使用尽可能大的批量大小，然后比较不同批量大小的性能；
• 小批量添加正规化的效果大，而大批量添加的正则化效果小，因此在适当平衡正规化效果的同时利用好它；
• 使用更大的批量通常会更好，这样就可以使用更大的学习率；

权重衰减：

• 网格搜索以确定适当的幅度，但通常不需要超过一个有效数字精度；
• 更复杂的数据集需要较少的正则化，因此设置为较小的权重衰减值，例如10^-4、10^-5、10^-6、0；
• 浅层结构需要更多的正则化，因此设置更大的权重衰减值，例如10^-2、10^-3、10^-4；

28、tanh和sigmoid谁收敛快

tanh，上面有说

29、BN的公式，和GN的区别

https://blog.csdn.net/qq_37100442/article/details/81776191

BN 前向传播的公式：

和 GN 的区别：

BN层是沿着维度C的方向，计算(,,)(N,H,W)的均值和方差；对于GN层，在某一层中，将一个样本的C个特征通道分成G组（默认情况下，=32G=32），每组中包含⌊⌋⌊CG⌋个特征通道。我们将使用每个样本下的每个分组来计算均值和方差，即计算××CG×H×W个值得均值和方差。

30、描述一下各类优化器及其公式

这一篇文章：https://blog.csdn.net/SHAOYEZUIZUISHAUI/article/details/81705001?utm_medium=distribute.pc_aggpage_search_result.none-task-blog-2_allfirst_rank_v2~rank_v25-1-81705001.nonecase&utm_term=%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0%E4%B8%AD%E7%9A%84%E5%90%84%E7%A7%8D%E4%BC%98%E5%8C%96%E5%99%A8%E6%80%BB%E7%BB%93

Batch gradient descent

每次更新我们需要计算整个数据集的梯度，因此使用批量梯度下降进行优化时，计算速度很慢，而且对于不适合内存计算的数据将会非常棘手。批量梯度下降算法不允许我们实时更新模型。

但是批量梯度下降算法能确保收敛到凸平面的全局最优和非凸平面的局部最优。

SGD(Stochastic gradient descent)

随机梯度下降算法参数更新针对每一个样本集x(i) 和y(i) 。批量梯度下降算法在大数据量时会产生大量的冗余计算，比如：每次针对相似样本都会重新计算。这种情况时，SGD算法每次则只更新一次。因此SGD算法通过更快，并且适合online。

但是SGD以高方差进行快速更新，这会导致目标函数出现严重抖动的情况。一方面，正是因为计算的抖动可以让梯度计算跳出局部最优，最终到达一个更好的最优点；另一方面，SGD算法也会因此产生过调。

Min-batch gradient descent

该算法有两个好处，1）：减少了参数更新的变化，这可以带来更加稳定的收敛。2：可以充分利用矩阵优化，最终计算更加高效。但是Min-batch梯度下降不保证好的收敛性。

Batch gradient descent、SGD、min-batch gradient descent算法都需要预先设置学习率，并且整个模型计算过程中都采用相同的学习率进行计算。这将会带来一些问题，比如

1）：选择一个合适的学习率是非常困难的事情。学习率较小，收敛速度将会非常慢；而学习率较大时，收敛过程将会变得非常抖动，而且有可能不能收敛到最优。

2）：预先制定学习率变化规则。比如，计算30轮之后，学习率减半。但是这种方式需要预先定义学习率变化的规则，而规则的准确率在训练过程中并不能保证。

3）：上述三种算法针对所有数据采用相同的学习速率，但是当我们的数据非常稀疏的时候，我们可能不希望所有数据都以相同的方式进行梯度更新，而是对这种极少的特征进行一次大的更新。

4）：高度非凸函数普遍出现在神经网络中，在优化这类函数时，另一个关键的挑战是使函数避免陷入无数次优的局部最小值。

Momentum

动量可以加速SGD算法的收敛速度，并且降低SGD算法收敛时的震荡。

通过添加一个衰减因子到历史更新向量，并加上当前的更新向量。当梯度保持相同方向时，动量因子加速参数更新；而梯度方向改变时，动量因子能降低梯度的更新速度。

NAG(Nesterov accelerated gradient)

滚雪球游戏中，我们希望有一个智能的雪球，它能够预知运动的方向，以至于当它再次遇到斜坡的时候会减慢速度。我们可以通过计算来渐进估计下一个位置的参数（梯度并不是完全更新），即为

Adagrad

Adagrad优化算法是一种自适应优化算法，针对高频特征更新步长较小，而低频特征更新较大。因此该算法适合应用在特征稀疏的场景。

先前的算法对每一次参数更新都是采用同一个学习率，而adagrad算法每一步采用不同的学习率进行更新。我们计算梯度的公式如下：

SGD算法进行参数更新的公式为：

Adagrad算法在每一步的计算的时候，根据历史梯度对学习率进行修改

这里G是一个对角矩阵，对角线元素是截止当前时刻的历史梯度的平方和，eta是一个平方项。如果不执行均方根操作，算法的性能将会变得很差。

G包含了针对所有历史梯度的平方和，因此我们可以用矩阵元素乘的形式来表达上式：

Adagrad算法的主要优点是它避免了手动调整学习率的麻烦，大部分的实现都采用默认值0.01。

Adagrad算法主要的缺点在于，其分母梯度平方的累加和。因为每次加入的都是一个正数，随着训练的进行，学习率将会变得无限小，此时算法将不能进行参数的迭代更新。

Adadelta

Adadelta算法是adagrad算法的改进版，它主要解决了adagrad算法单调递减学习率的问题。通过约束历史梯度累加来替代累加所有历史梯度平方。这里通过在历史梯度上添加衰减因子，并通过迭代的方式来对当前的梯度进行计算，最终距离较远的梯度对当前的影响较小，而距离当前时刻较近的梯度对当前梯度的计算影响较大。

通常，我们设置lambda参数为0.9。为了清楚的表达，这里我们再次列出SGD算法的计算公式：

而adagrad算法的计算公式为：

这里我们简单的替换对角矩阵G为E（带衰减的历史梯度累加）

上式分母正好是均方误差根（RMS），这里我们用简写来表达：

作者提到参数更新应该有相同的假设，因此我们定义另一个指数衰减平均，这里采用的是参数更新的平方

因为t时刻，RMS[]项未知，因此我们采用先前的参数RMS对当前时刻进行渐进表示。最终我们有如下表达式：

采用Adadelta算法作为模型优化器算法时，我们已经不需要设置默认学习率。

RMSprop

RMSPprop算法和adadelta算法都是adagrad算法的优化版，用于解决adagrad算法学习率消失的问题，从最终的计算公式来看，RMSProp算法和Adadelta算法有相似的计算表达式

Adam

Adam算法是另一种自适应参数更新算法。和Adadelta、RMSProp算法一样，对历史平方梯度v(t)乘上一个衰减因子，adam算法还存储了一个历史梯度m(t)。

mt和vt分别是梯度一阶矩（均值）和二阶矩（方差）。当mt和vt初始化为0向量时，adam的作者发现他们都偏向于0，尤其是在初始化的时候和衰减率很小的时候（例如，beta1和beta2趋近于1时）。

通过计算偏差校正的一阶矩和二阶矩估计来抵消偏差：

利用上述的公式更新参数，得到adam的更新公式：

AdaMax

Adam算法对历史梯度的二范数进行计算

这里我们可以改为计算历史梯度的p范数

较大的p，将会使数值计算不稳定，这也是实际中大量使用1范数和2范数的原因。然而，无穷范数则是稳定的。鉴于此，作者提出Adamax算法，通过计算无穷范数，使矩估计收敛到稳定。为了和adam算法区分开，这里用u(t)表示：

替换adam算法参数更新公式分母，可得：

Nadam

Adam算法可以看作是RMSProp算法和Momentum的结合版。RMSProp算法通过对历史梯度平方乘上衰减因子来计算v(t)，动量则计算历史梯度。我们知道NAG算法优于momentum算法。这里nadam结合了adam算法和NAG算法，为了使用NAG算法，我们需要修改动量表达式m(t)。

首先，回忆动量更新表达式

将第二项代入第三项中有

从上述分析可知，动量考虑了历史动量方向和当前梯度方向。NAG算法通过在梯度计算项中加入历史动量信息来达到一个更精确的计算，因此我们修改公式为：

Dozat提出对NAG进行如下修改：不再进行两次动量计算（一次更新梯度，一次更新参数），而是采用直接更新当前的参数：

注意这里我们没有采用前一时刻的动量m(t-1)，而是采用当前的动量m(t)。为了加入NGA算法，我们同样可以替换先前的动量向量为当前的动量向量。首先，我们回忆adam更新规则

将上式1、2带入式3中可得

通过使用动量的偏差校正估计，可得

现在我们加入nesterov 动量，采用当前动量的偏差校正估计替换前一时刻动量的偏差校正估计，可得：

31、过拟合的解决办法

上面已经有了

32、空洞卷积

https://zhuanlan.zhihu.com/p/59899622

① 引入背景：图像分割FCN中有两个关键，一个是pooling减小图像尺寸增大感受野，另一个是upsampling扩大图像尺寸。在先减小再增大尺寸的过程中，肯定有一些信息损失掉了，那么能不能设计一种新的操作，不通过pooling也能有较大的感受野看到更多的信息呢？答案就是dilated conv。

② 原理：Dilated/Atrous Convolution(中文叫做空洞卷积或者膨胀卷积) 或者是 Convolution with holes 从字面上就很好理解，是在标准的 convolution map 里注入空洞，以此来增加 reception field。相比原来的正常convolution，dilated convolution 多了一个 hyper-parameter 称之为 dilation rate 指的是kernel的间隔数量(e.g. 正常的 convolution 是 dilatation rate 1)。

③ 作用：

• 扩大感受野：在deep net中为了增加感受野且降低计算量，总要进行降采样(pooling或s2/conv)，这样虽然可以增加感受野，但空间分辨率降低了。为了能不丢失分辨率，且仍然扩大感受野，可以使用空洞卷积。这在检测，分割任务中十分有用。一方面感受野大了可以检测分割大目标，另一方面分辨率高了可以精确定位目标。
• **捕获多尺度上下文信息：**空洞卷积有一个参数可以设置dilation rate，具体含义就是在卷积核中填充dilation rate-1个0，因此，当设置不同dilation rate时，感受野就会不一样，也即获取了多尺度信息。*多尺度信息在视觉任务中相当重要啊。*

33、卷积神经网络在maxpooling处怎么反向传播误差

原文作者说的：把每个样本的梯度传给最大值对应的位置，其他位置为0就可以了

网上搜的：https://blog.csdn.net/weixin_41683218/article/details/86473488

池化层的反向传播：

① mean pooling: mean pooling的前向传播就是把一个patch中的值求取平均来做pooling，那么反向传播的过程也就是把某个元素的梯度等分为n份分配给前一层，这样就保证池化前后的梯度（残差）之和保持不变

② max pooling：max pooling也要满足梯度之和不变的原则，max pooling的前向传播是把patch中最大的值传递给后一层，而其他像素的值直接被舍弃掉。那么反向传播也就是把梯度直接传给前一层某一个像素，而其他像素不接受梯度，也就是为0。

34、MSE和MAE对学习结果的影响

• 相对于使用MAE计算损失，使用MSE的模型会赋予异常点更大的权重
• 如果训练数据被异常点所污染，那么MAE损失就更好用（比如，在训练数据中存在大量错误的反例和正例标记，但是在测试集中没有这个问题）。
• MAE存在一个严重的问题（特别是对于神经网络）：更新的梯度始终相同，也就是说，即使对于很小的损失值，梯度也很大。这样不利于模型的学习。为了解决这个缺陷，我们可以使用变化的学习率，在损失接近最小值时降低学习率。

35、Adam和dropout的原理

adam 上面写了，这里说 dropout

dropout的原理是使一部分神经元失效，仅仅保留一部分神经元的计算，因此添加dropout层的位置为cnn或者lstm层之后。机器学习的目标是优化方差和偏差，而过拟合是机器学习常见的问题，dropout能降低过拟合，其原因在于dropout使部分神经元失效之后，每次模型都只学到部分的特征（类似于随机深林），降低了模型了方差。

36、attention 注意力的理解

https://zhuanlan.zhihu.com/p/35571412

• attention机制的本质是从人类视觉注意力机制中获得灵感(可以说很‘以人为本’了)。大致是我们视觉在感知东西的时候，一般不会是一个场景从到头看到尾每次全部都看，而往往是根据需求观察注意特定的一部分。而且当我们发现一个场景经常在某部分出现自己想观察的东西时，我们就会进行学习在将来再出现类似场景时把注意力放到该部分上。这可以说就是注意力机制的本质内容了。至于它本身包含的‘自上而下’和‘自下而上’方式就不在过多的讨论。
• Attention机制其实就是一系列注意力分配系数，也就是一系列权重参数罢了。

37、反卷积相比其他上采样层（pixelshuffle）的缺点，棋盘格现象怎么产生的

https://blog.csdn.net/qq_16949707/article/details/82558852

• 反卷积有个比较大的问题就是，如果参数配置不当，很容易出现输出feature map带有明显棋盘状的现象
• 棋盘格现象：通过神经网络生成的图片，放大了看会有棋盘的现象
• 原因：混叠现象造成的，反卷积时，到stride和ksize 不能整除时，就会有这种现象，二维图像的时候更显著。

数学题

1、现在有一堆点，求一个点到每个点的距离之和最小，证明这个点是质心。

2、$y=\sqrt{x^2}$的可导性

先化简为绝对值函数。定义域为R。可导要求左导数、右导数存在且相等，所以函数在x等于0处不可导，其余处可导。

3、调和级数的敛散性

4、概率题

1、甲扔n次骰子，取其中最大的点数作为它的最终点数，乙扔一次骰子得到点数，求乙的点数大于甲的概率。

2、某种病的发病率为1/100，某种检测该病的技术检测正确率为99/100，现有一人被检测到生病的概率为p，求他真实生病的概率是多少？

3、在上一问的基础上，现在连续两次检测为有病才会停止检测，求检测次数的期望值。

4、概率题， 10个人里每个人在10分钟内的任何一个分钟到达的概率是均匀分布的，问所有人都到达的时刻在几分钟时概率最大。

5、A和B比赛，A、B获胜的概率分别是0.6、0.4，如果你是A，3局2胜和5局3胜你会选择哪个。如果A和B比赛无数局，A获胜的概率是多少

6、概率题：x, y服从0-1均匀分布，求x+y<1的概率？x, y, z服从0-1均匀分布，求x+y+z<1的概率？

7、已知var(x),var(y),E(x),E(y)求 Var(x*y)

8、人群中男人色盲的概率为5%，女人为0.25%。从男女人数相等的人群中随机选一人，恰好是色盲。求此人是男人的概率。

全概率公式一般不会考。面试或者笔试这种一定是考贝叶斯公式。这种题把事件用变量定义好就简单了，分清哪个是条件概率。

设“一个人是男人”是事件A,事件A非为“一个人是女人”。“一个人患色盲”为事件B。需要求的是逆概率P(A|B)。

9、在网游中，野怪被杀死时，有p=0.2的概率掉落一把宝剑。野怪的死亡是独立事件。玩家持续杀死了10个野怪，求掉落4把宝剑的概率。

独立重复试验，二项分布。C(10,4)*(p^4)*((1-p)6)。

10、一辆巴士载了25人，路经10个车站。每个乘客以相同的概率在各个车站下车。如果某个车站有乘客要下车，则大巴在该站停车。每个乘客下车的行为是独立的。记大巴停车次数为X，求X的数学期望（要求通过编程求数学期望）。

根据数学期望的定义进行计算，跟一面一样，继续蒙特卡洛模拟。面试官问我，如果乘客变为50人，估计一下数学期望会变为多少，应该是接近10。

import random
n=10000
cnt=[0]*11
for i in range(n):
    arr=[0]*10
    for j in range(25):
        rnd=random.randint(0,9)
        arr[rnd]+=1
    SUM=0
    for j in range(10):
        if arr[j]>0:
            SUM+=1
    cnt[SUM]+=1
ans=0.0
for i in range(11):
    ans+=i*cnt[i]/n
print(ans)

11、求几何分布的期望

12、考虑五局三胜和三局两胜的情况，哪种更公平之类的。

https://zhuanlan.zhihu.com/p/61655460

算法题

1、二叉树的左视图（或者右视图）

原题

2、二维矩阵中是否存在某个元素

原题

3、给定一个有向无环图，按拓扑排序的顺序输出节点

4、旋转数组中搜索某个目标值

原题

5、二维矩阵，求连通区域数量（连通的定义： 两个像素是四邻接的邻居，并且像素值的差的绝对值小于等于16，那么这两个像素是连通的）。

6、链表倒序

原题

7、两个链表找交点

原题

8、二分、堆排序

9、单通道的图像卷积（带padding）

10、顺时针输出矩阵

原题

11、最近公共祖先

原题

12、线段树的一些操作

13、模糊匹配（一个字串里有些地方可能是错的或者缺了，在原来的地方找到最有可能的位置）。

14、编辑距离

原题

15、由0和1组成的二维矩阵，找出1的最大连通域，计算其面积

16、长度为n的字符串中包含m个不同的字符，找出包含这m个不同字符的最小子串

17、下一个全排列

18、长度为n的数组中有一个数字出现了n/2次，快速找到这个数

19、编程题，LEETCODE 448

原题

20、LEETCODE 121、123

原题

21、带括号的加减乘除字符串运算

原题

22、二分法查找位置

原题

23、最长连续子序列

原题

24、实现矩阵相乘

25、两数之和的所有组合

26、Leetcode124

原题

27、数组前半部分和后半部分有序，然后排序

归并排序

28、判断输入字符串开始或者结尾是否包含非法字符串

29、斐波那契数列

(递归/备忘录/两变量记录)

30、lc 23

原题

31、组合

原题

32、一个数组，一个数出现一次，其他数出现两次，求出现一次的那个数。一个数组，两个数出现一次，其他数出现两次，求那两个数。

第一个所有数字进行异或，结果就是要求的值。

第二个需要用更复杂一点的位运算。

33、旋转数组查找

34、一个人初始体力为m，起始点为0，终点为n。一路上有毒蘑菇和体力蘑菇，用v_i表示，吃了会有体力的增加或减少，走多少步就消耗多少体力。问这个人能否到达终点，如果能，最小体力是多少。

35、两个栈模拟一个队列

36、二叉树的序列化与反序列化

前序遍历和中序遍历

37、小兔的棋盘

就是矩阵的路径数，动态规划原题

38、寻找迷宫中的最短路径

39、leetCode 76. Minimum Window Substring. Hard

40、一个正整数数组，寻找连续区间使得和等于target

41、Leetcode #72（hard）, 字符串的编辑距离

原题

42、一亿个浮点数，大小不超过2^32，均匀分布在值域内，求最快的排序方法；分析排序方法的复杂度

43、完全二叉树输出最后一个节点

https://leetcode.com/problems/count-complete-tree-nodes/

计算机基础知识

操作系统

1、堆空间栈空间了解吗？

https://blog.csdn.net/mormont/article/details/53511441

1.栈区（stack）：又编译器自动分配释放，存放函数的参数值，局部变量的值等，其操作方式类似于数据结构的

栈。

2.堆区（heap）：一般是由程序员分配释放，若程序员不释放的话，程序结束时可能由OS回收，值得注意的是他与

数据结构的堆是两回事，分配方式倒是类似于数据结构的链表。

2、2.5亿个整数找不重复的整数，内存无法一下存下这2.5亿个数，怎么做。

关键词：Bitmap 算法

采用2-Bitmap（每个数分配2bit，00表示不存在，01表示出现一次，10表示多次，11无意义）进行，共需内存2^32 * 2 bit=1 GB内存，还可以接受。然后扫描这2.5亿个整数，查看Bitmap中相对应位，如果是00变01，01变10，10保持不变。所描完事后，查看bitmap，把对应位是01的整数输出即可。

3、如何判断机器是大端模式还是小端模式

https://blog.csdn.net/banana1006034246/article/details/78021198

将整数存储后再以字符读出进行比较：

声明一个十六进制数 a = 0x12345678，然后一个指针 p 指向它，如果 p[0] == 0x12, 说明和声明顺序一致，是大端模式，如果 p[0] = 0x78，说明是小端模式。

4、如何从用户态进入内核态

答案：软件中断。

我们所说的用户态到内核态的切换，其实就是一个进程通过系统调用到内核的一些接口。从而实现切换。而该系统调用切换时通过软件中断来完成。

5、进程线程的区别，优缺点

• 一个程序至少有一个进程，一个进程至少有一个线程
• 进程有独立的内存单元，多个线程共享内存
• 进程是操作系统资源分派的基本单位，线程是CPU调度和分派的基本单位。
• 进程开销大，线程开销小。

6、TLB 原理，translation lookaside buffe，快表

快表

① 用途：加速虚拟地址到物理地址的转换。

② 理解：是一个特殊的高速缓存，存有页表的一部分或全部内容，CPU 读取数据时需要访问两次主存，使用快表只需要一次。

③ 流程：首先查询快表，如果在快表中，直接读取物理地址；如果不在快表中，从页表中读取，放入快表中再返回；快表填满后，按照一定的策略淘汰。

计算机网络

1、多线程怎么通信？

• wait / notify 方法

• 共享内存

• 信号量

python

1、python 的 GIL

① 概念：GIL的全称是 Global Interpreter Lock，全局解释器锁。Python最初的设计理念在于，在任意时刻只有一个线程在解释器中运行，python 的多线程不是真正的多线程，是通过解释器的分时复用实现的。GIL 就是一把全局锁，

② 优点：GIL可以保证我们在多线程编程时，无需考虑多线程之间数据完整性和状态同步的问题

③ 缺点：我们的多线程程序执行起来是“并发”，而不是“并行”。因此执行效率会很低，会不如单线程的执行效率

2、python 的 dict 如何实现的

dict的底层是依靠哈希表(Hash Table)进行实现的，使用开放地址法解决冲突.（当冲突的时候，将数据放在另一个空位）

3、python 多线程如何占满核

官方的不行就，因为由 GIL 锁，除非重写一个不带 GIL 的解释器，但是可以用多进程模拟多线程。

4、python的动态数组是如何实现的

顺序表（就是数组），存储的只是地址的引用，大小不够就扩容，扩容是直接扩大四倍。

其他问题

8、给图片去水印怎么去？

① 深度学习建模

② 传统方法：https://blog.csdn.net/zhangjunhit/article/details/77680140

11、哈希表了解吗？有哪些解决冲突方法？

概念

能够通过 key --> value 的形式访问的数据结构，python 里面是字典，java 里面是 HashMap.

建立过程

1、建立一个数组

2、对键求哈希值

3、对数组长度求余数，放在对应位置

冲突解决

（拉链法）如果出现冲突，则在后方使用链表；（开放地址法）另找一个空位。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3MjrZmBM-1604755234252)(http://127.0.0.1:60823/paste-2ddc714768c6fba408231649dd83acd8cfac7c78.jpg)]

14、解释下raw图像和rgb图像的区别

https://www.cnblogs.com/crazybingo/archive/2012/03/22/2412498.html

Raw RGB 每个像素只有一种颜色（R、G、B中的一种）；
RGB 每个像素都有三种颜色，每一个的值在0~255之间；
在手机摄像头的测试过程中，由sensor输出的数据就是Raw data（Raw RGB），经过彩色插值就变成RGB

15、了解其他色彩空间格式嘛？

https://zhuanlan.zhihu.com/p/28741691

1.RGB颜色空间：依据人眼识别的颜色定义出的空间,可表示大部分颜色

2.CMY/CMYK颜色空间：工业印刷采用的颜色空间。

3.HSV/HSB颜色空间 ：为了更好的数字化处理颜色而提出来的。

4.HSI/HSL颜色空间 ：为了更好的数字化处理颜色而提出来的。

5.Lab颜色模型：由CIE(国际照明委员会)制定的一种色彩模式。

16、饱和度、亮度这些了解嘛

https://www.cnblogs.com/yxnchinahlj/archive/2011/03/04/1970735.html

饱和度是指图像颜色的彩度.对于每一种颜色都有一种人为规定的 标准颜色，饱和度就是用描述颜色与标准颜色之间的相近程度的物理量。调整饱和度就是调整图像的彩度。将一个图像的饱和度条为零时，图像则变成一个灰度图像

亮度就是各种颜色的图形原色（如RGB图像的原色为R、G、B三种或各种自的色相）的明暗度，亮度调整也就是明暗度的调整。亮度范围从 0到255，共分为256个等级。而我们通常讲的灰度图像，就是在纯白色和纯黑色之间划分了256个级别的亮度，

22、数据结构：红黑树如何插入，简单一些的，AVL 树呢？

红黑树：插入的时候可能需要变色、左右旋转

AVL 树就是平衡二叉树，插入的时候，需要旋转。（具体也可以不看，情况太多了）

（1）右旋:节点插入在最小不平衡节点的左子树的左子树上。此时以最小不平衡子树的根节点为旋转节点，进行右旋。

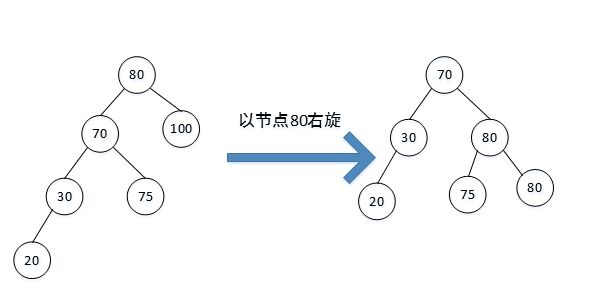
（2）左旋: 节点插入在最小不平衡节点的右子树的右子树上。此时以最小不平衡子树的根节点为旋转节点，进行左旋。

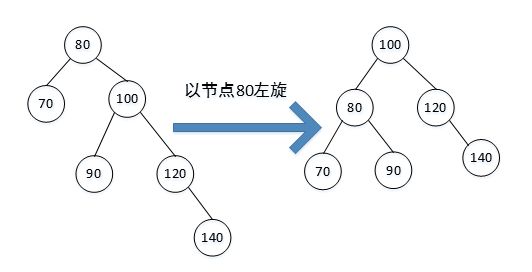
（3）右左：节点插入在最小不平衡节点的左子树的右子树上面。以最小不平衡节点进行右旋，再以最小不平衡子树的根节点左旋。

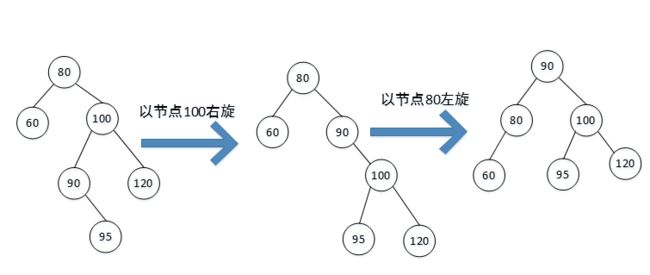
（4）左右：节点插入在最小不平衡节点的左子树的右子树上面。以最小不平衡节点进行左旋，再以最小不平衡子树的根节点右旋。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-elUQPuLG-1604755234266)(https://img-blog.csdn.net/20170713215031006?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvdGlhbnl1eGluZ3h1YW4=/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast)]

96、对称加密和非对称加密

直接说不知道就行了，这个原理没了解过的话，不好说。