Coursera Algorithm Ⅱ week4 编程作业 Boggle

代码地址：https://github.com/RedemptionC/CourseraAlgorithms/tree/master/boggle

本题基本与leetcode212 单词搜索Ⅱ（https://leetcode-cn.com/problems/word-search-ii/）相同，实现trie的时候还可以把208 实现trie（208. 实现 Trie (前缀树)）做了~

要求是给出一个board，上面每一个格子之上都有一个字母，题目会给出一个字典，里面有一些预定的单词，我们要做的是找出board相邻（上下左右对角线）的格子上的字母，如果能组成字典里的单词，就计分

所以本质上是个搜索问题：我们可以建立一个set，把字典里的单词都加入，然后在board上搜索，如果当前连成的单词在字典里，就积分

关键在于，要实现高效的查字典，我们不能直接用hashset里的contains，应该用startwith这种函数，一旦字典里没有当前这种字符串作为开头的单词，马上返回

这里我们要实现trie（字典树），来实现高效的查询

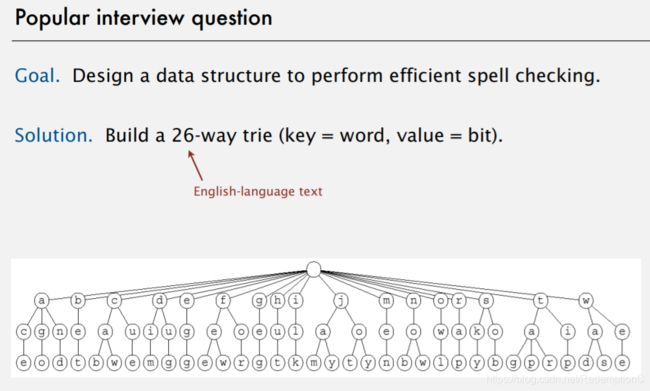
因为本题里的元素都是大写字母，只有26种，为了简单起见，我实现的是26 way trie

差不多就是这种：

上代码：

Trie

public class Trie {
    private class Node {
        private Integer value;
        private Node[] next = new Node[26];
    }

    private Node root;
    private int count;// for setting value

    /** Initialize your data structure here. */
    public Trie() {
        root = new Node();
        count = 0;
    }

    private Node insert(String word, int val, Node node, int d) {
        if (node == null) {
            node = new Node();
        }
        if (d == word.length()) {
            node.value = val;
            return node;
        }
        int c = word.charAt(d) - 'A';
        node.next[c] = insert(word, val, node.next[c], d + 1);
        return node;
    }

    /** Inserts a word into the trie. */
    public void insert(String word) {
        insert(word, count, root, 0);
        count++;
    }

    private boolean search(String word, Node node, int d) {
        if (node == null) {
            return false;
        }
        if (d == word.length()) {
            if (node.value == null)
                return false;
            else
                return true;
        }
        int c = word.charAt(d) - 'A';
        return search(word, node.next[c], d + 1);
    }

    /** Returns if the word is in the trie. */
    public boolean search(String word) {
        return search(word, root, 0);
    }

    // 注意，这里是判断是否有以prefix为前缀的字符串在trie里，所以当d==len后，下一步是判断node.next是否有不为null
    private boolean startsWith(String prefix, Node node, int d) {
        if (d > prefix.length()) {
            return false;
        }
        if (node == null) {
            return false;
        }
        // 按说这里不能只根据next[i]不为空就判断存在，但是因为这里没有delete，所以只要next[i]不为空
        // 那么对应的value也不为空（也就是不会被删除）
        if (d == prefix.length()) {
            return true;
        }
        int c = prefix.charAt(d) - 'A';
        return startsWith(prefix, node.next[c], d + 1);
    }

    /** Returns if there is any word in the trie that starts with the given prefix. */
    public boolean startsWith(String prefix) {
        return startsWith(prefix, root, 0);
    }

    public static void main(String[] args) {
        Trie trie = new Trie();
        trie.insert("APPLE");
        System.out.println(trie.search("APPLE"));   // 返回 true
        System.out.println(trie.search("APP"));    // 返回 false
        System.out.println(trie.startsWith("APP")); // 返回 true
        trie.insert("APP");
        System.out.println(trie.search("APP"));     // 返回 true

    }
}

/**
 * Your Trie object will be instantiated and called as such:
 * Trie obj = new Trie();
 * obj.insert(word);
 * boolean param_2 = obj.search(word);
 * boolean param_3 = obj.startsWith(prefix);
 */

boardSolver

import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.SET;
import edu.princeton.cs.algs4.StdOut;

public class BoggleSolver {
    private Trie set;
    private int rows, cols;
    private BoggleBoard boggleBoard;
    private boolean[][] marked;
    // 上下左右，左上，右上，左下，右下
    private final int[] drow = { -1, 1, 0, 0, -1, -1, 1, 1 };
    private final int[] dcol = { 0, 0, -1, 1, -1, 1, -1, 1 };

    // Initializes the data structure using the given array of strings as the dictionary.
    // (You can assume each word in the dictionary contains only the uppercase letters A through Z.)
    public BoggleSolver(String[] dictionary) {
        set = new Trie();
        for (String s : dictionary) {
            set.insert(s);
        }
    }

    private boolean outOfBound(int row, int col) {
        return row < 0 || row >= rows || col < 0 || col >= cols;
    }

    private void dfs(SET rs, int row, int col, StringBuilder sb) {
        char c = boggleBoard.getLetter(row, col);
        sb.append(c == 'Q' ? "QU" : c);
        if (!set.startsWith(sb.toString())) {
            return;
        }
        marked[row][col] = true;
        if (sb.length() >= 3) {
            String t = sb.toString();
            if (set.search(t)) {
                rs.add(t);
            }
        }
        for (int i = 0; i < 8; i++) {
            int tRow = row + drow[i];
            int tCol = col + dcol[i];
            if (outOfBound(tRow, tCol) || marked[tRow][tCol]) {
                continue;
            }
            dfs(rs, tRow, tCol, new StringBuilder(sb));
            marked[tRow][tCol] = false;
            // if (row == 0 && col == 0)
            //     printMarked();
        }
    }

    private void printMarked() {
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                System.out.printf("%b ", marked[i][j]);
            }
            System.out.println();
        }
    }

    // Returns the set of all valid words in the given Boggle board, as an Iterable.
    public Iterable getAllValidWords(BoggleBoard board) {
        SET rs = new SET<>();
        boggleBoard = board;
        //dfs:以所有的点作为起点，然后向左右，上下，对角线，搜索
        rows = board.rows();
        cols = board.cols();
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                // FIXTHIS:这里是可以仅new一次的
                marked = new boolean[rows][cols];
                dfs(rs, i, j, new StringBuilder());
            }
        }
        return rs;
    }

    // Returns the score of the given word if it is in the dictionary, zero otherwise.
    // (You can assume the word contains only the uppercase letters A through Z.)
    public int scoreOf(String word) {
        if (!set.search(word))
            return 0;
        int len = word.length();
        if (len < 3)
            return 0;
        if (len == 3 || len == 4)
            return 1;
        if (len == 5)
            return 2;
        if (len == 6)
            return 3;
        if (len == 7)
            return 5;
        // if (len >= 8)
        return 11;
    }

    public static void main(String[] args) {
        In in = new In(args[0]);
        String[] dictionary = in.readAllStrings();
        BoggleSolver solver = new BoggleSolver(dictionary);
        BoggleBoard board = new BoggleBoard(args[1]);
        int score = 0;
        for (String word : solver.getAllValidWords(board)) {
            StdOut.println(word);
            score += solver.scoreOf(word);
        }
        StdOut.println("Score = " + score);
        // System.out.println(solver.scoreOf("STONES"));
    }

}