基于传统优化方法的图像去模糊文献综述（部分经典文献）

由于图像模糊在生活中是广泛存在的，图像去模糊问题从上个世纪起就得到了关注和研究。从上个世纪60年代起，为了解决图像去模糊问题，首次提出将图像问题转化到频域中来解决，提出了逆滤波、维纳滤波等经典的算法。但基于频域的图像去模糊算法需要准确的知道模糊的退化类型，并且对噪声敏感，进而提出基于空域的估计算法。常见的基于空域的估计算法有：差分复原算法、最小二乘算法、最大熵算法等。近年来，图像去模糊算法更是取得了较大的突破。随着时间发展，去模糊问题已经衍生出许多的方法和类别。按照去模糊算法的方法进行分类大致可以分为基于优化的去模糊方法和基于深度学习去模糊的方法；按照输入进行分类可以分为：基于单帧输入的去模糊算法和基于多帧输入的去模糊算法；按照退化类型进行分类可以分为运动模糊，高斯模糊，散焦模糊，湍流模糊等；按照模糊核是否已知进行分类可分为盲目去模糊问题和非盲目去模糊问题；按照退化是否一致性可以分为空变模糊和空不变模糊等。分类如图1所示。本文主要按照方法的分类来进行阐述。

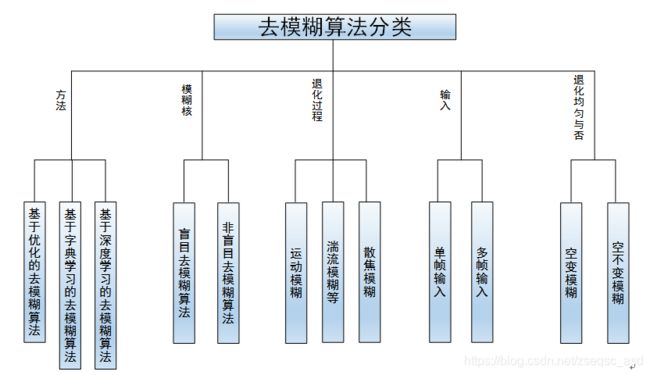
图1 去模糊问题分类

基于最大后验概率的图像去模糊算法

基于最大后验概率框架的图像去模糊算法的核心思想是找到某个解（清晰图像），使得其后验概率值最大。即为在已知退化图像y的条件下，找到一组清晰图像x和模糊核k，使得概率$P\left(y|x,k\right)$最大，其数学表示为
$\hat{x},\hat{k}=\arg \underset{x,k}{\min }P\left(y|x,k\right).$
根据贝叶斯公式，可将上式转化为
$\hat{x},\hat{k}=\arg \underset{x,k}{\min }P\left(x,k|y\right)P\left(x\right)P\left(k\right),$
其中，$P\left(x,k|y\right)$为似然概率，其概率分布即为噪声n的分布。$P\left(x\right)$和$P\left(k\right)$分别为清晰图像x和模糊核k的先验概率。
根据MAP框架建模的方式不同，去模糊算法可以分为两类：基于稀疏先验的图像去模糊算法，修改数据项的图像去模糊算法。

基于稀疏先验的图像去模糊算法

基于MAP的先验算法是通过修改MAP框架的先验项来克服图像去模糊的病态问题，从而复原出清晰图像。在通常情况下，该类方法建立在线性退化模型的基础上，假设噪声服从高斯分布，并且其均值为0方差为$\sigma $。而图像的先验概率和模糊核的先验概率分别为
$P\left(x\right)\propto e^{-\rho \left(x\right)},P\left(k\right)\propto e^{-\rho \left(k\right)},$
则可以得到基于最大后验概率的图像去模糊框架为
$\hat{x},\hat{k}=\arg \underset{x,k}{\min }{\Vert k\otimes x-y\Vert }_2^2+{\lambda }_1\rho \left(k\right)+{\lambda }_2\rho \left(x\right),$
其中，KaTeX parse error: Can't use function '\]' in math mode at position 17: …{\lambda }_{1}}\̲]̲和\[{ {\lambda }_…分别为图像的先验概率。
特别地，这里的框架是一种盲目反卷积框架，对于非盲目反卷积同样具有类似的框架
$\hat{x}=\arg \underset{x,k}{\min }{\Vert k\otimes x-y\Vert }_2^2+{\lambda }_1\rho \left(x\right).$ (2.5)
该类方法就是要通过设计$\rho \left(k\right)$和$\rho \left(x\right)$，实现约束病态问题具有可逆的过程并最终收敛至清晰图像。

（1）基于梯度域或灰度域的统计先验
2005年Roth等人通过统计自然图像的梯度分布，发现图像服从如图2（a）所示的中拖尾分布。2008年，Shan等人根据重拖尾分布提出一种更稀疏的分段式先验，
$\rho \left(x\right)=\{\begin{array}{c}-k\left|x\right|\\ -\left(a{x}^2+b\right)\end{array}\begin{array}{c}x<=l_t\\ x>l_t\end{array},$
其中，x表示图像的梯度，$l_t$表示两个函数连接的位置。其函数如图2（b）所示。这种服从重拖尾分布的梯度先验在初始的迭代过程中赋予正则化较大的权值，使得图像具有抑制图像细小的纹理而保留大尺度结构的作用，有利于准确的估计模糊核。除此之外， Shan等人引入平滑区域的掩模来抑制图像去模糊问题中的振铃现象，因此具有较好的清晰图像复原的效果。

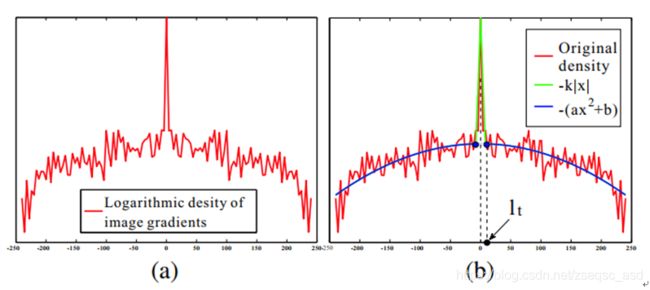
图2 去模糊问题分类(a) 自然图像梯度统计图，（b）分段先验曲线图

2011年，Krishman等人使用了一组$l_1/l_2$ 范数先验作为先验项，其数学表达为$\frac{{\Vert x\Vert }_1}{{\Vert x\Vert }_2}$，其主要的思想是将图像梯度的$l_2$范数作为迭代过程中的$l_1$范数权重，实际上依然是在提取$l_1$范数的特征。这样设计的先验同样利用了$l_1$范数的稀疏性，隐式的抑制了图像的纹理性的细小结构保留大尺度结构，并且$l_2$范数作为权值在一定程度上避免了MAP问题取向于一个模糊的解。
在上述的基础上，2013年，Li等人还提出一种非自然的$L_0$稀疏性先验。其先验的表示形式为
$\rho \left(x\right)=\sum _i\varphi \left({\partial }_{\ast }{x}_i\right),$
其中，$\varphi \left({\partial }_{\ast }{x}_i\right)=\{\begin{array}{c}\frac{1}{{\epsilon }^2}{\left|{\partial }_{\ast }{x}_i\right|}^2\\ 1\end{array}\begin{array}{c}\left|{\partial }_{\ast }{x}_i\right|<=\epsilon \\ \end{array}$。
与其他先验（Shan和 范数）相比，提出的非自然的 稀疏性先验具有更强的稀疏性，如图3。并且和零范数的先验更为接近，但与此同时能够转换为凸优化问题并使用半二次分离法进行求解。在拥有较快的求解速度的同时具有较好的复原效果。

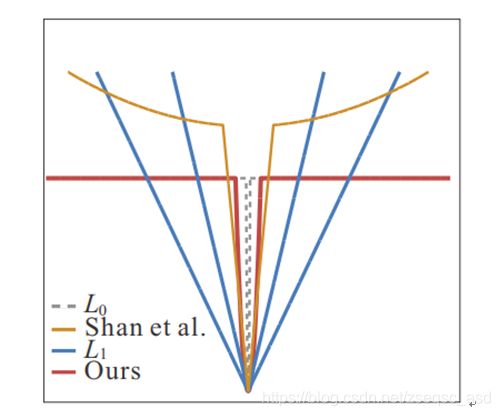
图3 不同先验项函数示意图

此外，而在文字图像去模糊的问题上，Pan等人通过统计文字图像梯度从而提出一种基于 范数的图像先验，采用硬阈值公式求解，在文字图像去模糊问题中取得了突破性的进展。

（2）通道先验
通道先验也是一种通过静态统计模糊图像和清晰图像手动设计的一种稀疏性先验。区别于直接统计图像的灰度特征和梯度特征不同的是，通道先验是通过统计通道的像素。2009年，He等人首次提出暗通道先验，并使用在图像去雾中，使得图像去雾取得了突破性的进展。图像暗通道是指在图像块的彩色图像的通道中至少有一个通道的像素值趋近于零。
2016年，Pan等人首次提出将暗通道先验应用到图像去模糊领域，指出清晰图像相比模糊图像具有更稀疏的暗通道值，建立暗通道稀疏性先验${\Vert D\left(I\right)\Vert }_0$，其中
$D\left(I\right)\left(x\right)=\underset{y\in N\left(x\right)}{\min }\left(\underset{y\in \left\{r,g,b\right\}}{\min }{I}^c\left(y\right)\right)$ ，
$N\left(x\right)$是以x为中心的图像块，并将非线性操作$D\left(I\right)$等价于线性操作算子进行求解。实验结果验证了其有效性。
2017年，Yan等人在暗通道先验的基础上进一步提出亮通道先验，与暗通道先验先反的是，亮通道指在图像块的彩色图像的通道中至少有一个通道拥有较大的像素值。其数学定义为$B\left(I\right)\left(x\right)=\underset{y\in N\left(x\right)}{\max }\left(\underset{y\in \left\{r,g,b\right\}}{\max }{I}^c\left(y\right)\right)$。
文章在建立先验时，综合了暗通道稀疏性先验${\Vert D\left(I\right)\Vert }_0$和亮通道稀疏性先验${\Vert 1-B\left(I\right)\Vert }_0$进行求解。
统计图像的灰度值、梯度值或通道先验设计的基于静态统计先验的算法，一定程度上区分了清晰图像和模糊图像，便于针对不同场景中的图像，设计特定的先验知识，有利于减轻图像去模糊的病态问题。但Levin等人提出，这种基于稀疏性设计的先验存在着收敛的问题，优化的结果容易得到平凡解，即估计的图像结果趋向于模糊图像，而不是清晰图像，为了避免这种情况需要精心的设计先验和初始值。另一方面，这种手动设计的先验没有利用数据内在的分布，具有一定的局限性。

基于变分贝叶斯框架的去模糊算法

基于变分贝叶斯的图像去模糊算法的核心思想是考虑所有可能的解，所以理论上是更稳健的。Fergus使用混合高斯模型通过贝叶斯推断学习一个梯度先验，Levin提出这种基于贝叶斯推断的方法可以避免MAP问题中出现的趋向于平凡解的问题。但由于需要遍历整个解空间，算法的速度太慢，无法达到实用的要求。

基于边缘估计的去模糊算法

基于边缘估计的盲目反卷积算法的核心思想是通过一些滤波、图像增强等算法显式地估计出具有大尺度边缘、细小边缘被抑制的图像，然后基于这些显著边缘来估计模糊核。基于边缘估计的去模糊算法速度快并且已经证明在实际应用中非常有效，但是很难去分析，因为并不是基于模型通过优化得到，而是通过一些启发式的步骤的组合得到。
基于边缘估计的盲目反卷积算法能够成功估计出模糊核的原因是其能够估计出图像中的大尺度边缘，抑制细小的边缘。文献中指出大尺度边缘更利于真实模糊核的估计，而细小的边缘起着相反的作用。文中采用双边滤波器提取图像的大尺度边缘，将提取的边缘图像用于模糊核估计。算法流程如图所示。

图4 算法流程图
Xu等人提出纹理平滑策略,用于提取大尺度边缘，指导图像去模糊。因为估计的清晰图像中大尺度边缘不够显著，而细小边缘抑制不够时，基于最大后验概率模型的去模糊算法存在收敛问题。使用稀疏先验能够基本解决收敛问题的原因是稀疏先验倾向于梯度的稀疏性，也就是图像中小梯度被抑制，而大梯度保持，这正好和基于边缘估计的机理吻合。