维吉尼亚密码的破解算法及python代码实现

1. 密文描述

密文1

密文：
krkpekmcwxtvknugcmkxfwmgmjvpttuflihcumgxafsdajfupgzzmjlkyykxdvccyqiwdncebwhyjmgkazybtdfsitncwdnolqiacmchnhwcgxfzlwtxzlvgqecllhimbnudynagrttgiiycmvyyimjzqaxvkcgkgrawxupmjwqemiptzrtmqdciakjudnnuadfrimbbuvyaeqwshtpuyqhxvyaeffldmtvrjkpllsxtrlnvkiajfukycvgjgibubldppkfpmkkuplafslaqycaigushmqxcityrwukqdftkgrlstncudnnuzteqjrxyafshaqljsljfunhwiqtehncpkgxspkfvbstarlsgkxfibffldmerptrqlygxpfrwxtvbdgqkztmtfsqegumcfararhwerchvygczyzjaacgntgvfktmjvlpmkflpecjqtfdcclbncqwhycccbgeanyciclxncrwxofqieqmcshhdccughsxxvzdnhwtycmcbcrttvmurqlphxnwddkopqtehzapgpfrlkkkcpgadmgxdlrchvygczkerwxyfpawefsawukmefgkmpwqicnhwlnihvycsxckf

密钥： crypt (长度为5)

明文:
  I am alive here, my beloved, for the reason to adore you. Oh!How anxious I have been for you and how sorry I am about all you must have suffered in having no news from us. May heaven grant that this letter reaches you. Do not write to me, this would compromise all of us and above all,do not return under any circumstances. It is known that it was you who helped us to get away from here and all would be lost if you should show yourself.We are guarded day and night. I do not care you are not here. Do not be troubled on my account. Nothing will happen to me. The national assemble will show leniency. Farewell the most loved of men. Be quiet if you can take care of yourself.For myself I cannot write any more, but nothing in the world could stop me to adore you up to the death.

密文2

密文：
cbkznkiyjsrofgnqadnzuqigscvxizgsjwucusrdkxuahgzrhywtvdjeiuwsrrtnpszbvpzncngztbvsrnzuqigscvfjwqgjwcytwdazuqigscvfjwqgjwjhkfdylmcbmhonbmbvdnvbmwbnacjaphhonbmbvdnvbmwbnaublsbdnjjneoroyfmxfhixpzpcozzuqigscvxcvhdmfgxmgovzsqmvzyvwyzmsczoajsejifoakdcrehwhgdehvmtnmvvmesvzifutzfjzoalwqztunwvdvmfhesvzifutzfjzoalwqztunpsnoyfleoxdetbwfsoyfjmfhjuxuagnarsfqydoyfjzsrzeujmfhjuubihrjdfinwsnepcawdnkbobvnmzucmghijjmbscjejnapddehlmqddmfxncqbfpxwfejifpqzhikiyaiozimubwuzufazsdjwdiudzmztivcmgp

密钥：uiozvrb(长度为7)

明文：
  It was the best of times.It was the worst of times. It was the age of wisdom. It was the age offoolishness. It was the epoch of belief. It was the epoch of incredulity. It was the season of light. It was the season of darkness. It was the spring of hope. It was the winter of despair.We had everything before us. We had nothing before us. We were all going direct to heaven. We were all going direct the other way. In short, the period was so, far like the present period, that some of its noisiest authorities insisted on its being received, for good or for evil, in the superlative degree of comparison only.

2. 破解原理

2.1 重合指数法确定密钥长度

  重合指数是指字符串中两个随机元素相同的概率，记为$\text{IC}$。设某种语言由$n$个字母组成，每个字母$i$发生的概率为$P_i\left(1\le i\le n\right)$，则：
$$IC=\sum _{i=1}^n{P}_i^2\text{，}\left(1\right)$$
  现实世界中密文有限，故从密文计算的重合指数总是不同于理论值，所以一般用$\text{IC}$的无偏估计值：
$$IC=\sum _{i=1}^n\frac{x_i\left(x_i-1\right)}{L\left(L-1\right)}.\left(2\right)$$
  其中，$x_i$是密文中i出现的次数，L表示密文长度，n表示字母数，此处n=26。
  对于英文字符串，通过词频统计可以得到26个英文字母出现的期望概率。通过大量的英文样本，利用公式（1）可得一般英文文本重合指数值：
$$IC=\sum _{i=0}^{25}{P}_i^2=0.065\text{，}\left(3\right)$$
  对于一个完全随机的字符串，其重合指数值：
$$IC=26{\left(\frac{1}{26}\right)}^2=0.038.\left(4\right)$$
  因为0.065与0.038间隔的充分远，所以能够通过这种方式确定密钥长度。具体计算步骤如下：
  Step1：初始化d = 1。
  Step2：将密文分成d个子串，分别对每一个子串利用公式（2）计算其重合指数，及它们的平均值。若d为密钥长度，那么该平均值的IC值将接近于0.065。
  Step3：d = d+1，若d < 10重复步骤二。
  Step4：比较每一个d下的重合指数平均值，取最接近0.065的d值即为所求。
  以密文1为例，利用上述算法，得到部分结果见表1。

表1 密文1密钥长度与重合指数对应表

  从计算结果可以确定密文1的密钥字长度为5，此时每一个子串的平均重合指数为0.06254。
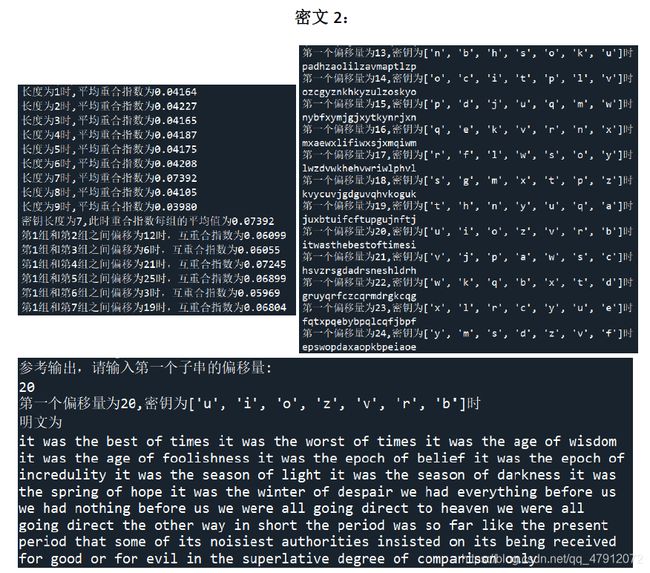
  对于密文2采用同样的计算方法得到密钥字长度为7，此时平均重合指数为0.07392。对于其余的情况，平均重合指数均在0.035-0.046之间波动。

2.2 互重合指数确定子串间相对偏移

  从以上结论可知密钥字长度。下面本文将采用互重合指数法来确定相对位移，其精确定义如下。
  已经确定密钥字长度为m，密文子串$Y_i$中的各个密文字母都是由同一个单表代换得到。设密钥为$K=K_1{K}_2\dots K_m$，可估算$M{I}_c\left(Y_i,Y_j\right)$的值。显然，$Y_i$中的一个随机元素与$Y_j$中的一个随机元素同时为第h个英文字母的概率$P_{h-K_i}{P}_{h-K_j},0\le h\le 25$，这里下标运算为模26运算。因此有

$$M{I}_c\left(Y_i,Y_j\right)\approx \sum _{h=0}^{25}{P}_{h-K_i}{P}_{h-K_j}=\sum _{h=0}^{25}{P}_h{P}_{h+K_i-K_j}\left(5\right)$$
  该估计值仅仅依赖于$s_{ij}=\left(K_i-K_j\right)\text{mod}26$，称其为$Y_i$和$Y_j$的相对位移。易得，当相对位移s为0时，互重合指数估计接近0.065；当s不为0时，这些估计值在0.031-0.045之间波动。因此可以确定子串之间的相对位移，以密文1为例得到结果见表2。

表2 密文1互重合指数表

  第1组和第2组之间偏移为11时，互重合指数为0.06141；
  第1组和第3组之间偏移为4时，互重合指数为0.06148；
  第1组和第4组之间偏移为13时，互重合指数为0.05907；
  第1组和第5组之间偏移为9时，互重合指数为0.06198。
  于是密钥字为 $K=\left(K_1,K_1-11,K_1-4,K_1-13,K_1-9\right)$

2.3 密钥字的确定

  对$K_1$遍历26个英文字母后，可以得到26种可能的密钥。对每一个密钥均对密文进行解密。通过分析“明文”的前20个字母，可以确定：
  密文1密钥为crypt, k=(2,-9,-2,-11,-7) ；
  密文2密钥为uiozvrb, k=(20,8,14,-1,-5,17,1) 。

2.4 密文破解

  利用上述密钥对密文进行破解，引入wordninja库对英文明文进行分词操作。最后，为明文进行标点调整。

3. 破解代码

Python代码(代码说明见代码注释)
运行环境：python 3.7 + numpy、wordninja第三方库

'''维吉尼亚破解'''
import numpy as np
import wordninja

def alpha(cipher): #预处理,去掉空格以及回车 
    c = ''
    for i in range(len(cipher)):
        if(cipher[i].isalpha()):
            c += cipher[i]
    return c

def count_IC(cipher): #给定字符串计算其重合指数 
    count = [0 for i in range(26)]
    L = len(cipher)
    IC = 0.0
    for i in range(len(cipher)):
        if(cipher[i].isupper()):
            count[ord(cipher[i])-ord('A')] += 1
        elif(cipher[i].islower()):
            count[ord(cipher[i])-ord('a')] += 1
    for i in range(26):
        IC += (count[i]*(count[i]-1))/(L*(L-1))
    return IC

def count_key_len(cipher,key_len): #对字符串按输入个数进行分组，计算每一组的IC值返回平均值
    N = ['' for i in range(key_len)]
    IC = [0 for i in range(key_len)]
    for i in range(len(cipher)):
        m = i % key_len
        N[m] += cipher[i]
    for i in range(key_len):
        IC[i] = count_IC(N[i])
    #print(IC)
    print("长度为%d时,平均重合指数为%.5f" % (key_len,np.mean(IC)))
    return np.mean(IC)    

def length(cipher): #遍历确定最有可能的密钥长度返回密钥长度 
    key_len = 0
    mins = 100
    aver = 0.0
    for i in range(1,10):
        k = count_key_len(cipher,i)
        if(abs(k-0.065)<mins):
            mins = abs(k-0.065)
            key_len = i
            aver = k
    print("密钥长度为%d,此时重合指数每组的平均值为%.5f" % (key_len,aver))
    return key_len
    
def count_MIC(c1,c2,n): #n=k1-k2为偏移量,计算c1,c2互重合指数MIC
    count_1 = [0 for i in range(26)]
    count_2 = [0 for i in range(26)]
    L_1 = len(c1)
    L_2 = len(c2)
    MIC = 0
    for i in range(L_1):
        if(c1[i].isupper()):
            count_1[ord(c1[i])-ord('A')] += 1
        elif(c1[i].islower()):
            count_1[ord(c1[i])-ord('a')] += 1         
    for i in range(L_2):
        if(c2[i].isupper()):   
            count_2[(ord(c2[i])-ord('A')+n+26)% 26] += 1
        elif(c2[i].islower()):
            count_2[(ord(c2[i])-ord('a')+n+26)% 26] += 1   
    for i in range(26):
        MIC += count_1[i]*count_2[i]/(L_1*L_2)
    return MIC

def count_n(c1,c2): #确定两个子串最优的相对偏移量n=k1-k2
    n = 0
    mins = 100
    k = [0.0 for i in range(26)]
    for i in range(26):
        k[i] = count_MIC(c1,c2,i)
        #print(i,k[i])  
        if(abs(k[i]-0.065)<mins):
            mins = abs(k[i]-0.065)
            n = i      
    return n
        
def  group_k(cipher,key_len):#完成分组操作并计算每一组与第一组的最优相对偏移量并返回
    N = ['' for i in range(key_len)]
    MIC = [0 for i in range(key_len)]
    s = [0 for i in range(key_len)]
    for i in range(len(cipher)): #对密文进行分组 
        m = i % key_len
        N[m] += cipher[i] 
    for i in range(1,key_len):  #计算与第一组之间的相对偏移量 
        s[i] = count_n(N[0],N[i])  # s[i] = k1-k(i+1) 
        MIC[i] = count_MIC(N[0],N[i],s[i])  # MIC[i] = MIC(1,i+1)
        print("第1组和第%d组之间偏移为%d时，互重合指数为%.5f" % (i+1,s[i],MIC[i]))
    return s    

def miyao(key_len,s,k):  #k为第一个子串的移位，输出密钥并返回密钥所有字母的下标
    mi = ['' for i in range(key_len)] 
    for i in range(key_len):
        s[i] = -s[i]+k   #k2=k1-n
        mi[i] = chr((s[i]+26) % 26 + ord('a'))
    print("第一个偏移量为%d,密钥为%s时" % (k,mi))
    return s

def the_end(cipher,key_len,s):#输入密文密钥返回明文结果 
    plain ='' 
    i = 0 
    while( i < len(cipher)):
        for j in range(key_len):
            if(cipher[i].isupper()):
                plain += chr((ord(cipher[i])-ord('A')-s[j]+26) % 26 + ord('A'))
            else:
                plain += chr((ord(cipher[i])-ord('a')-s[j]+26) % 26 + ord('a'))
            i+=1
            if(i == len(cipher)):
                break 
   # print(plain) 
    return plain
             
if __name__ == "__main__":
    fp = open("密文2.txt","r")
    cipher = '' 
    for i in fp.readlines():
        cipher = cipher + i    
    fp.close()
    cipher = alpha(cipher)
    key_len = length(cipher)
    s = group_k(cipher,key_len)
    m = s.copy()
    for k in range(26):
        s = m.copy() 
        s = miyao(key_len,s,k)
        plain = the_end(cipher,key_len,s)
        print(plain[0:20]) #输出部分明文确定偏移量k1
    print("参考输出，请输入第一个子串的偏移量:",end='')
    k = int(input())
    m = miyao(key_len,m,k)
    plain = the_end(cipher,key_len,m)

    '''对英文文本进行分词'''
    word = wordninja.split(plain)
    plain = ''
    for i in range(len(word)):
        plain += word[i]
        plain += ' '
    print("明文为\n"+plain)

部分输出截图：

参考文献

python实现维吉尼亚秘钥破解

一种新式Vigenere密码的破译和研究

Python英文文本分词(无空格)模块wordninja的使用实例