堆排序（Heapsort）

1.堆排序基本介绍:

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。
堆是一个近似完全二叉树的结构，并同时满足堆积的性质：
即子结点的键值或索引总是小于（或者大于）它的父节点。
堆排序的平均时间复杂度为 Ο(nlogn)
堆排序视频详解入口

大顶堆：
每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；
小顶堆：
每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

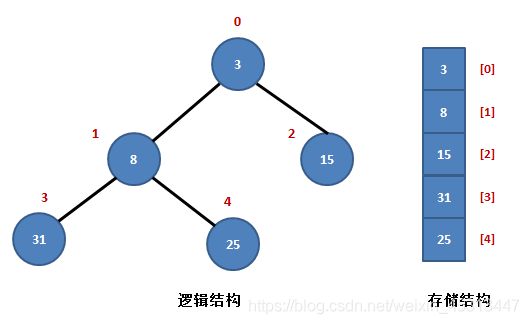
2.堆的基本结构（小顶堆）：

设当前元素在数组中以R[i]表示，那么：
(1) 它的左孩子结点是：R[2*i+1];

(2) 它的右孩子结点是：R[2*i+2]
(3) 它的父结点是：R[(i-1)/2];

(4) R[i] <= R[2*i+1] 且 R[i] <= R[2i+2]。

3.建堆（大堆）和排序（升序）：

初始无序数组a[1, 3, 4, 5, 2, 6, 9, 7, 8, 0]：

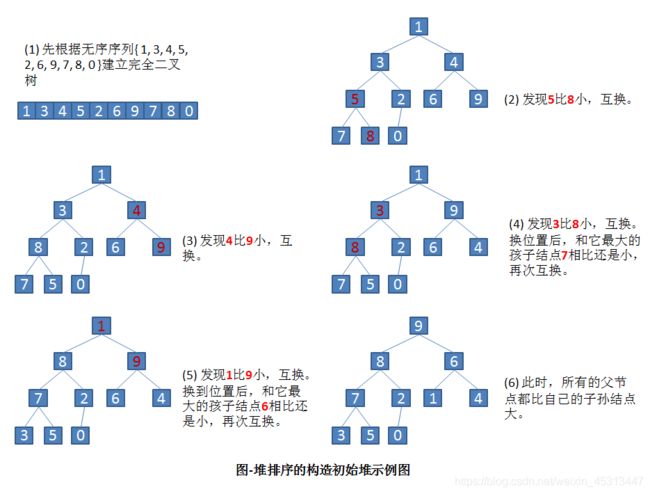
建堆源代码：

void AdjustDown(int* a, int n, int root)
{
     
	//父亲节点
	int parent = root;
	//左孩子节点
	int child = parent * 2 + 1;
	while(child < n) {
     
		//在左孩子和右孩子里面找大的
		if (child + 1 < n && a[child + 1] > a[child]) {
     
			child++;
		}
		//如果孩子结点大于父亲节点进行交换
		if (a[child] > a[parent]) {
     
			int temp = a[child];
			a[child] = a[parent];
			a[parent] = temp;
			parent = child;
			child = parent * 2 + 1;
		}
		else
			break;
	}
}

建好大堆以后的原本数组变为：a[9,8,6,7,2,1,4,3,5,0],
此时还是无序但是可通过以下操作就可将数组变为升序：
1.堆顶（a[0])和最后一个(a[9])进行交换。
2.排除最后一个以后，对剩下的从新进行大堆调整。
3.循环如此，直到最后一个。
4.过程展示如下：

堆排序源代码：

void HeapSort(int *a,int n )
{
     
	//从最后一个叶节点的父亲节点开始从下往上逐个建堆。
	for (int i = (n - 2) / 2; i >= 0; i--)
		AdjustDown(a, n, i);
	int end = n - 1;
	//把堆顶数据和最后一个进行交换并对剩下的从新进行堆调整。
	while (end > 0) {
     
		int temp = a[0];
		a[0] = a[end];
		a[end] = temp;
		AdjustDown(a, end, 0);
		end--;
	}
}

堆排序以后：a[0,1,2,3,4,5,6,7,8,9]。

4.源代码：

#include
//自顶向下的建堆（大堆）：
void AdjustDown(int* a, int n, int root)
{
     
	//父亲节点
	int parent = root;
	//左孩子节点
	int child = parent * 2 + 1;
	while(child < n) {
     
		//在左孩子和右孩子里面找大的
		if (child + 1 < n && a[child + 1] > a[child]) {
     
			child++;
		}
		//如果孩子结点大于父亲节点进行交换
		if (a[child] > a[parent]) {
     
			int temp = a[child];
			a[child] = a[parent];
			a[parent] = temp;
			parent = child;
			child = parent * 2 + 1;
		}
		else
			break;
	}
}
//堆排序
void HeapSort(int *a,int n )
{
     
	//从最后一个叶节点的父亲节点开始从下往上逐个建堆。
	for (int i = (n - 2) / 2; i >= 0; i--)
		AdjustDown(a, n, i);
	int end = n - 1;
	//把堆顶数据和最后一个进行交换并对剩下的从新进行堆调整。
	while (end > 0) {
     
		int temp = a[0];
		a[0] = a[end];
		a[end] = temp;
		AdjustDown(a, end, 0);
		end--;
	}
}
int main()
{
     
	int a[9] = {
      12,3,65,84,76,32,4,7,78 };
	HeapSort(a, 9);
	for (int i = 0; i < 9; i++) {
     
		printf("%d ", a[i]);
	}
	return 0;
}

5.结果展示：