自动机与形式语言复习：文法，DFA，NFA与正则表达式

前言

自动机与形式语言通过规范化的文法，逻辑地表示某些字符串。此外，通过对串的成分进行分析，同时给出一组状态与对应的状态转移，组成自动机。DFA 和 NFA 是两种自动机，都能够判断某些串是否能够被接收，走到接收状态就算接收。

---

还有三天。。。考完就可以 run 了，好耶！

我只考三门，都觉得复习很吃力，但是别人往往考 10 门，还比我先考，还游刃有余。这令我深刻的认识到：我是啥β

原本打算摸了，但是想到不复习真的可能会挂科，就来更新一下复习笔记了。

注：
因为我上了一学期课，从来没有认真听课超过 10 min，作业都是抄别人的
于是这篇复习笔记很可能错漏百出，并且伴有缺内容，缺重点等等问题
⚠ 请谨慎食用 ⚠

文法

通过文法可以规范化的表达某种语言（语言就是串的集合），我们通过四元组来表示一个文法：

$$G=(V,T,P,S)$$

其中 V 是 variable，表示变量，即状态的集合。

T 是 terminal，终极符，通过一系列的终极符号 T，在不同的变量（V）中进行跳转。比如 V1 可以通过接收字符 T，从而转到 V2 状态。

S 是 start symbol，为文法的开始符号，其中 S 属于状态集合 V

P 为 production，即产生式。产生式告诉我们状态之间的联系，比如一个状态 V 可以产生一个字符 0，那么有：

$$V\to 0$$

当然也可以递归地进行产生，比如产生的结果中，包含自己：

$$V\to 0V$$

一个规范化的四元组长这样：

$$G=(\{A,B\},\{0,1\},\{A\to 0,A\to 1A,B\to 0A,B\to 1\},B)$$

通过产生式，推出一个字符串产生的过程，叫做推导。例子如下，给出文法 G，写出句子 aaa 的推导过程

$$G=(\{A\},\{a\},\{A\to a\mid aA\},A)$$

推导的过程如下：

$$\begin{gathered} A\to aA,使用产生式A\to aA \\ aA\to aaA,使用产生式A\to aA \\ aaA\to aaa,使用产生式A\to a \end{gathered}$$

归约则是和推导（又称为派生）相反的过程，通过句子推导出文法。

DFA

DFA 即为确定的有穷状体自动机，和文法不同，文法注重描述一个串是如何产生的。而 DFA 则注重于观察该串是否能被某些文法接收。

通过五元组：

$$M=(状态集合,输入字母表,转移函数,起始状态,接收状态集合)$$

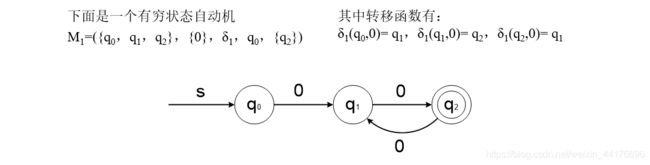
来描述一个 DFA。其中落入接收状态的串是能够被 DFA 识别的。比如：

此外，DFA 还应该有陷阱状态，表示当前串无法被接收时，状态就落入陷阱状态。比如有如下的例子，qt 就是陷阱状态，表示读取到不被接受的串：

通过【即时描述】来表达一个自动机接收某个串的过程。即时描述通过状态 q 在串上不停滑动，生动地表示了接收的过程，如下图：

NFA

NFA 意为不确定的有穷状体自动机。DFA 一次只能通过一个输入的字符，跳转到一个单独的状态。而 NFA 则允许通过一个输入的字符，跳转到多个状态。比如下图，q0 接收 0 可以跳转到 q1 或者 q0：

如果说 DFA 是单线程的话，NFA 就是多线程。如果说 DFA 是 DFS（深搜）的话，NFA 就是 BFS（广搜），这样是否容易理解了？

NFA 转换为 DFA

其实 NFA 和 DFA 是等价的，因为 DFA 是一次跳转到一个状态，而 NFA 是一次跳转到一个状态的集合。

如果把 NFA 的状态集合视为 DFA 的一个状态，那么就能实现 NFA 到 DFA 的转换，这个思想叫做子集构造。

比如将如下的 NFA 转为 DFA：

首先根据起始状态 q0，到达两个不同的状态集合，分别是 {q0, q1} 和 {q0, q2}

因为把状态集合看作是 DFA 的状态，那么我们得到了两个新状态，分别是 {q0, q1} 和 {q0, q2}，下图的绿色标记了这两个新状态：

然后来判断新状态 {q0, q1} 的状态转移。因为组合了状态 q0 和 q1 的状态转移，我们将原 NFA 的状态转移结果取并集，作为该状态的新转移（下图红色箭头）。这里只给出接收 0 的箭头，1 的同理，于是又产生了新的状态 {q0, q1, q3} ，如下图：

同理，对 {q0, q2} 如法炮制，我们取原 NFA 的 q0 和 q2 的状态转移结果的并集。产生新状态 {q0, q2, q3}，如下图：

对两个新状态也是如法炮制：

DFA，完成了！

ε-NFA

ε-NFA 允许通过空字符，即 ε 来转移到新的状态。

对于 ε-NFA，可以对其进行空拓展，将其转为一般的 NFA。因为接收到输入字符 a，也可以认为是接收到 aε，aεε，εεa，εa，即多个空字符！而且空字符可以任意地组合在有效字符 a 的前缀或者后缀。

空拓展可以通过 ε 来转移到任意状态，只要 NFA 有对应的边就允许任意输入字符沿着这些 ε 的边进行转移，最终达到一个闭包（即联通分量），下图展示了如何构建一个拓展的空闭包：

其实就是做了一次特殊的 dfs，只要遇到 ε 边，都无脑去搜它就好了。至此，ε-NFA 也可以转为普通的 NFA 了。因为普通 NFA 没有 ε 输入，我们只需要考虑正常的输入，进行 NFA 状态转移（边）的构造。

如下图绿色部分所示，这些是我们关心的状态转移：

正则表达式

注：
这个不是一般编程的正则表达式

正则表达式和文法类似，都是生成串的形式语言。正则表达式主要的操作有三个，分别是加法，连接和闭包。

加法能够将两个东西并行地联系起来，如果用集合来表示，就是并集。比如：

$$(0+1)\stackrel{表示的语言为}{⟶}\{0,1\}$$

通过 0 和 1 取并，生成的语言为 {0, 1}。

然后是连接（或者拼接？）连接运算则是按照顺序将两个表达式产生的串拼接起来，比如：

$$(01)\stackrel{表示的语言为}{⟶}\{01\}$$

那么最终表示的语言就只有 01 一个串了，注意顺序！

最后是闭包运算，闭包运算允许我们任意地将集合内的元素自由组合，比如：

$$(01{)}^{\ast }\stackrel{表示的语言为}{⟶}\{0,1{\}}^{\ast }$$

最后贴一张定义：

对应到自动机上，三种规则的构图如下：

1. 如果是 + 运算，那么分为两个分支进行接收
2. 如果是拼接运算，那么按照顺序进行接收
3. 如果是闭包运算，通过环路进行重复接收

下面来看一个例子：

图上作业法

图上作业法用于将一个自动机转换为正则表达式，换句话说，可以通过该方法查找出该自动机接收的串的正则表达式。

图上作业法的核心就算通过消除节点，来产生表达式。比如我们消除下图的 q2 节点，因为我们可以从 q1 通过正则表达式一步到 q3。

因此 q1 到 q3 的过程被我们描述为正则表达式，并且形成一条边。我们对 q2 的每个入度节点都要进行同样的操作（即连接 q2 的入节点和出节点），如下图：

事实上一次完整的图上作业法，第一步应该是虚拟起点和终点。将一个虚拟原点 X 通过空字符 ε 转移到初始状态。此外，将所有的接收状态通过 ε 引导到虚拟终点 Y，如下图：

通过消去 q2 节点，我们得到：

接着消去 q3 和 q4，这里我们得到两条边，我们可以通过加法合并他们：

最后消去 q1，得到最终的表达式：

泵引理

通过泵引理判断一个语言是否是正则语言，思路是反证法。

如果有 n 个状态，接收的串却长度大于 n，那么自动机（图）中必有环路。

先假设它是正则语言，我们沿着环路重复走 i 次，其中 i 可以是任意正整数，如果找到某个 i 使得该语言不被接收，那么就和假设矛盾，该语言就不是正则语言！

比如证明语言：

$$\{0^n{1}^n\mid n\ge 1\}$$
不是正则语言，通过泵引理的思路如下：

注：泵引理只能判断某个东西不是正则语言，不能判断它是正则语言。。。

极小化 DFA 算法

DFA 中可能存在冗余的状态，比如：

明明都是两条一样的路，你偏要分开来，于是 DFA 的极小化算法就算为了解决冗余的 DFA 而生。

---

首先定义一种状态：可区分。什么是可区分呢？接收相同的输入，却去到了不同的状态。

比如下图，q2 q3 接收 0，一个去到了接收状态，一个去了非接收状态，那么 q2，q3 可区分，因为他们有截然不同的特征：

此外，如果接收同样的输入，却去到了两个【可区分】的状态，那么这两个状态同样可区分。比如下图，q0，q1 接收 1，去到了可区分的 q2，q3，那么 q0，q1 同样是可区分的：

注意对所有的接收字符，都要进行判断，才能判断两个状态是否可区分。同时这个判断是递归进行的。

因为有时接收相同的输入，获得一组新的状态对 qi，qj 我们往往不知道他两是否可区分，于是问题转变为求 qi，qj 是否可区分，这就是递归！

此外，如果接收相同的输入，去到了相同的状态，那么他们不可区分，这意味着他们是等价的：

弄明白了啥可区分，不可区分，就可以开始进行算法了！

---

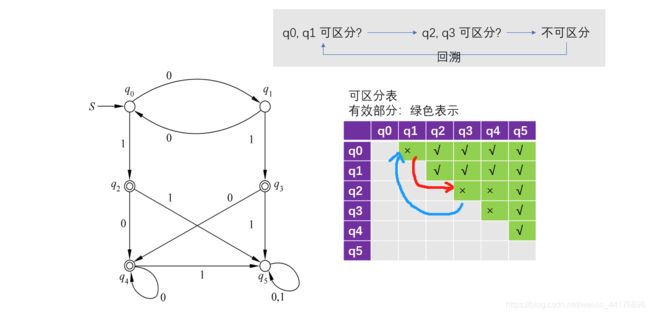
算法如下，首先准备一张可区分表。此外，可区分是相对的，ab 可区分意味着 ba 可区分，所以表的有效部分为上三角：

首先进行初始化，已知状态对 qi，qj 其中 qi 是接收状态，而 qj 不是接收状态，那么他们可区分。

• {q0, q1} 接收 1 时，前者去到接收状态 {q2, q3}，而 q5 接收 1 去到非接收状态 q5，于是 q0, q5 与 q1, q5 可区分
• {q2, q3, q4} 接收 1 时都去到非接受状态 q5，而 {q0, q1} 接收 1 去到接收状态 {q2, q3}，于是他们的 6 个组合，都可区分
• {q2,q3,q4} 接收 0 去到接收状态 q4，而 q5 接收 0 去到非接收状态 q5，于是他们的三种组合都可区分

根据上面三个判断，我们可以轻易地画出初始化的表格：

此外，如果接收到同一个输入，去到了相同的状态，那么他们不可区分（他们等价），于是有：

• {q2, q3, q4} 接收 0 都去到 q4，接收 1 都去到 q5，于是 q2, q3, q4 都不可区分

通过下图话 × 部分可以表示他们不可区分：

然后遍历表的每一项空缺，并且试图利用递归法判断该状态对是否可区分。这里只用判断 q0，q1 是否可区分。

因为 q0，q1 接收 1 能够到达 {q2, q3} 根据递归，问题转换为求 q2，q3 是否可区分！从表中看出他们不可区分，于是有：

那么有：

1. [q0, q1] 不可区分
2. [q2, q3, q4] 不可区分

于是将原来的自动机（图），根据状态（节点）之间是否可区分，将图划分为三个连通分支，分别是：

$$[q_0,q_1],[q_2,q_3,q_4],[q_5]$$

极小化后的 DFA 将一个连通分支视为单独的状态（或者说节点），根据节点进行转移。于是可以得出极小化后的 DFA：

FA 交集

前面在提及正则表达式的时候，我们可以通过加法（或者说两个单独的分支）来实现 FA 的并操作，这里以一道例题说明如何实现 FA 的交操作：

这里其实 1 不用管，因为满足 2，3 自然满足 1，根据 DFA 交集，我们首先构造满足 2 和 3 的 DFA：

紧接着取交集。从起始状态开始，我们将 1 和 3 状态合一。

• 在左边的自动机中，状态 1 接收到 1，转移到状态 1
• 在右边的自动机中，状态 3 接收到 1，转移到状态 4

于是我们起始状态为 13，在接收 1 后，状态转变为 14 了！对于其他的状态组合和输入组合如法炮制，最终得到如下的 DFA：

CFG，二义性与其化简

CFG，context-free grammar 又名上下文 免费 无关文法，是文法的一种特殊。它的定义是这样的，对于文法：

$$G=(V,T,P,S)$$

的产生式 P，除了 A → ε 的这种空产生式之外：

$$对于任意产生式：\forall \alpha \to \beta$$

产生的结果 β 都有如下规律：

$$|\beta |\ge |\alpha |且\beta \in V$$

意义就是对于任意的 A ∈ V，如果有产生式 A→B，无论 A 出现在什么位置，都可以通过将 A 替换成 B，而无需考虑 A 的上下文。

---

CFG 可以通过派生树来表示句子的生成过程。

可以看作是一颗树，生成树，通过先序遍历其所有叶子节点以获取最终生成的句子。此外，一个句子可能有不同的生成树，这叫做 二义性 。

---

CFG 可以被化简，因为尽管一个文法符合 CFG 的标准，但是其任然存在一些无关的东西。化简 CFG 的算法通常分为两个步骤：

1. 去除无法终止的变量
2. 去除无法到达的变量

而且这二者的顺序不可交换！证明过程略。

算法听起来有点抽象，那么什么叫无法终止的变量呢？就是无法派生出终极符的变量，比如下面的文法中的 A 变量：

$$G=(\{A,B\},\{a,b,c\},\{A\to aA\},A)$$

可以看到 A 变量能够生成 aA，但是无法终止，因为无论怎么生成，A 都消不掉，即无限递归。此外，如果产生式中没有出现的变量，比如上面文法的 B 变量就没有产生式，这表示一旦有一个 B，文法就会 ”卡死“，因为找不到 B 的产生式！

值得注意的是，一旦发现一个不可消去的变量 X，就要 “顺藤摸瓜” 地回溯，找到所有产生 X 的变量，并且这些产生 X 的变量也是不可消去的。

如图，还没消去的情况，因为 B 消除不掉，我们顺藤摸瓜，将 S→BB ，S→AB， C→ABa 也标记为无法终结的产生式：

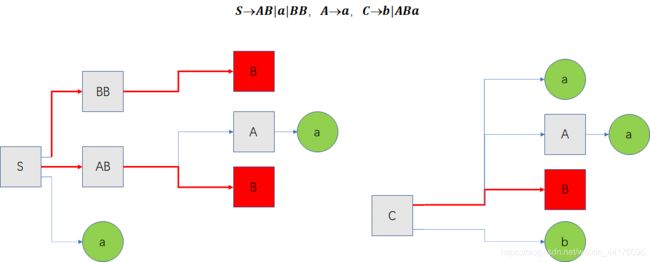
红色的叶子表示不可终结的变量 B，我们待消去的产生式如下：

$$\begin{gathered} S\to AB \\ S\to BB \\ C\to ABa \end{gathered}$$

消去无法终结的产生式之后的派生：

这里就来到了第二步：消除到达不了的变量。可以看到从 S 变量除法，无法到达 A，B 所以 A B 要被消去，消去之后的文法如下：

至此，CFG 化简完成。