正则表达式转NFA

前面一节介绍了NFA，这里讲介绍如何将正则表达式转化为等价的NFA。

1. 正则表达式的基本运算

正则表达式有三种基本的运算:

1) 连接(Concatenation), 例如 abc, 由a, b, c组成

2) 联合(Union), 例如 a|b|c, 表示a或者b或者c

3) Kleene闭包(Kleene *), 例如 (ab)*, 表示ab串不出现，或者出现1次或一次以上

其它的运算如+, {}等都可以用以上三种基本运算或者运算的组合来表示。

2. 将正则表达式转化为NFA

在NFA中，我们可以模拟正则表达式的三个基本操作。

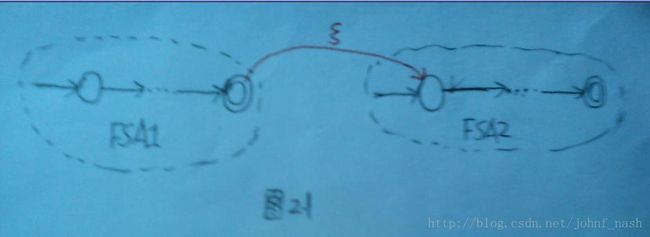
• 连接(Concatenation): 可以使用ε-转移，把FSA1的终极状态与FSA2的初始状态连接起来，如下图2.1所示
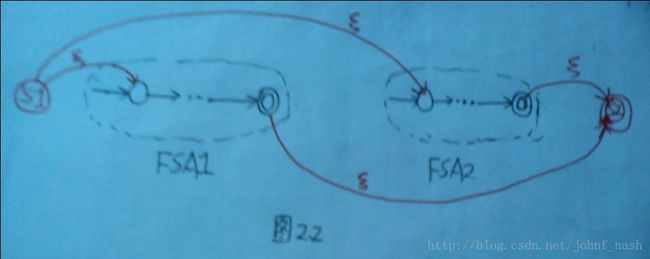
• 联合(Union): 可以增加一个新的初始状态s1和一个新的结束状态s2，并且从这个状态s1,用新的转移把它和两个自动机的初始状态连接起来。另外，从原来的两个自动机的终结状态，与新的终结状态s1连接起来，如下图2.2所示
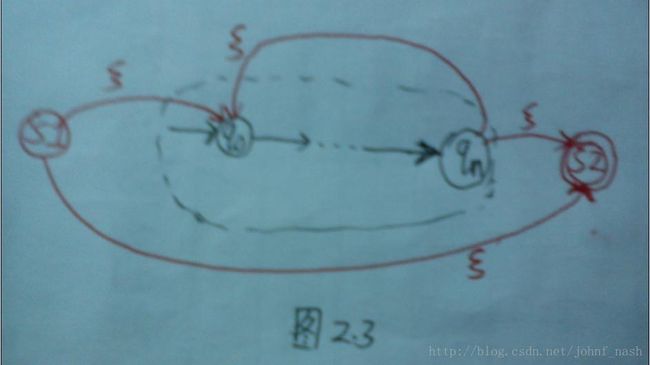
• Kleene闭包(Kleene *): 可以增加一个新的初始状态s1和一个新的结束状态s2。让新的开始状态s1指向原来的自动机的开始状态q0,让新的开始状态指向新的终极状态。另外，让原来的终结状态qn指向新的终极状态s2,让原来的终极状态qn指向原来的开始状态q0。如下图2.3所示                                             

                                                                                                                       图2.1 两个自动机的连接

                                             

                                                                         图2.2 两个自动机的联合(|)

                                             

                                                                            图2.3 自动机的闭包(Kleene *)

定义了自动机的这三种操作之后，就可以将正则表达式转化为NFA了。

3. 将正则表达式转化为NFA的代码实现

将正则表达式转化为NFA，我的思路是:

       1) 将正则表达式进行改写，使得符号的连接用运算符相连接，例如ab转化为a.b(.表示连接)。这样就得到

      了正则表达式的中缀表达式。

        2) 将1)中得到的中缀表达式转化为后缀表达式，这样就可以去掉'('和')'了。转化为中缀表达式是因为

       这样方便NFA构造。

       3) 解析2)中得到的后缀表达式。每当遇到操作数时就构造单个符号的NFA对象，压入栈中；

       每当遇到操作符(*, ., |)时,就从栈中取出操作数(NFA对象)，进行运算后(*, |, .)后，将得到的结果NFA

       压入栈中。最终栈中剩下的那个NFA对象就是与正则表达式等价的NFA对象。

 根据这个思路实现的核心算法如下:

/**
	 * 将正则表达式转化为等价的NFA对象
	 * @return 与该正则表达式等价的NFA对象
	 */
	public FA toNFA() {
		//在正则表达式中添加省略掉的毗邻运算符(.)
		String newRegexp = addRemovedConcatenationOP();
		System.out.println(newRegexp);
		//将添加毗邻运算符后的正则表达式转化为后缀表达式
		String postfix = infixToPostfix(newRegexp);
		System.out.println(postfix);
		//将用后缀表达式表示的正则表达式转化为等价的NFA对象
		return evaluateExpression(postfix);
	}

       其中 evaluateExpression 函数就是上面第3步中叙述的解析后缀表达式。其核心算法如下:

/**
     * 将用后缀表达式表示的正则表达式转化为等价的NFA对象
     * @param postfix 表示正则表达式的后缀表达式
     * @return 转化得到的NFA对象
     */
    private FA evaluateExpression(String postfix) {
        //创建一个操作数栈来存储操作数        
        Stack operandStack = new Stack();
        //分离操作数与操作符
        StringTokenizer tokens = new StringTokenizer(postfix, "*|.() ", true);
        //遍历符号
        while(tokens.hasMoreTokens()) {
            String token = tokens.nextToken().trim();
            if(token.length() == 0) {    //空格
                continue;
            } else if(token.charAt(0) == '*') {    //*操作符(单目运算符)
                NFA nfa = operandStack.pop();
                nfa.closure();            //进行闭包运算
                operandStack.push(nfa);
            } else if(token.charAt(0) == '|'
                    || token.charAt(0) == '.') {
                processAnOperator(operandStack, token);    //进行 '|' 运算 或 '.'运算
            }
            else {        //操作数
                operandStack.push(new NFA(token.charAt(0))); //为单个字符构造NFA对象
            }
        }
        return operandStack.pop();
    }

      其中 processAnOperator 函数根据当前操作符(| 或 .)的类型进行相应的NFA操作(union 或 concatenation)。

      如果还有什么疑问的话，可以到这里下载代码查看(注:这里的代码与之前的文章《DFA算法的实现与最小化》

一样的，如果你已经下载了，就不用再下载了)。或者在下面评论，我会尽快回复的。

4. 参考资料

1. 《自然语言处理综述》， [美] Danniel Jurafsky 著