一篇ACSAC的关于可编辑区块链的论文分析

Rewriting with Black-box Accountability：基于策略的Chameleon Hash对于具有黑盒问责的可编辑区块链)

前述

看了一个IT从业人员的日记，感觉时光走得太快，记忆留的太浅，如果不把一些东西记录下来，等到回忆往昔时会发现自己竟乏善可陈。于是决定把研究生看的有意义的论文记录一下，至少留作努力过的证明吧。。。如果能有一些csdn积分就更好了，没有也行
坐标 研一上的寒假，2021.1.13
导师让阅读ACSAC的论文，我选择的是 Applied Cryptography 专题。

关于paper

该论文是关于 可编辑区块链，采用Chameleon哈希算法和黑盒问责机制。
Keyword：Chameleon Hash、Blockchain Rewriting、Black-box Accountability

1.可编辑区块链

这篇很清晰：可编辑区块链：打破你对“不可篡改”的认知，但这样的区块链还安全吗.
众所周知，区块链的一个特性是不可篡改性。一方面在于交易内容全部映射到Merkle根，如果在本地篡改交易，则其他节点不会予以认可；另一方面在于区块链是有序的，已上链的区块不能更改否则会影响顺序。
但是对于这种存储信息的功能，修改的场景是不可避免的。如交易内容或金额的修改、区块里包含违法信息、上链后遇到意外需要撤销等。。。针对这种需求，有学者提出了可编辑区块链的概念，对于现有的Hash结构进行改造，留出修改后门，一种变色龙哈希Chamelelon Hash刚好满足该需求。
可编辑区块链在业界的争议还比较大，因为区块链的初衷就是去中心化，所有节点平等，公平公开。而一旦留出后门，显然谁掌握了后门，谁就成为区块链的中心化大boss。因此这一变动在迎合市场需要的同时背离了区块链的初衷。
另一方面，政府是希望看到区块链被监管的，区块链也不应该成为一些非法交易的庇护所，因此可以预想这种可编辑特性会不会在一定程度上推动区块链被承认和合法化的进程。
anyway，技术无罪，回归论文本身。

2.Chameleon Hash

这篇很好理解：变色龙哈希函数 Chameleon Hash 可变型区块链.
Hash：对于任意消息m，可将其映射为一个固定长度的串H(m).
区块链中，各个区块以Hash指针连接，主要依赖于Hash的三个特性：
（1）抗碰撞性：对于消息m，难以找到另一个消息m’，使H(m)=H(m’)；
（2）不可逆：已知一个消息的H(m)，难以倒过来推出m；
（3）不可预测：映射出的H(m)，是无法提前得知会映射出该结果的。
考虑到，如果对区块链修改，必然改变其Hash结果，无法获得其他节点认可，从而无法达到共识。因此，需要在不改变Hash的前提下修改。
这显然推翻了抗碰撞的特性，即 使新消息m’，哈希结果与原消息一致。满足这种特点的哈希就是Chameleon Hash（区块链中实际采用的是SHA256哈希），翻译过来是变色龙哈希，其原理如下：
类似于公钥加密，任何人都有做Chameleon Hash的公钥pk（public key），只有私钥sk（private key）拥有者可以获得m’的后门。变色龙哈希的三个阶段：
Step1：(sk, pk) = KeyGen($\lambda$)，首先构造满足安全常数$\lambda$的循环群G（生成元g），随机指数sk为私钥，公钥pk=g^sk；
Step2：H(m) = Hash(pk, m, r)，生成变色龙哈希的随机数为r，区块哈希值为H(m)=g^m*pk^r；
Step3：r’ = UForge(sk, m, r, m’)，将m篡改为m’后，希望找到一个随机数r’，使得H(m’)=H(m)，又H(m)=g^m·pk^r=g^m·(g^sk)^r=g^m+sk·r，H(m’)=g^m’·pk^r’=g^m’·(g^sk)^r’=g^{m’+sk·r’}，二者相等，因此已知m,m’,私钥sk,r，可得r’=(m+sk·r-m’)/sk.
变色龙哈希有基于因式分解的、基于格的和基于离散对数的。
这就是一种基于求解离散对数难题的举例，Cryptography - Chameleon Hash
大佬对它进行了Java实现。

3.黑盒问责

但是修改者也需要受到监管，防止有后门私钥的人对消息进行恶意修改，因此出现需求：如果对修改后的交易没有争议，那么交易修改者仍然是匿名的；如果出现争议，黑盒问责保证了任何用户都可以识别这个可疑的修改者，并且修改后的交易版本可以一一映射到对应的修改者。

该论文是在以上思想的基础上提出框架PCHBA，该框架的一个独特特性是，它不允许交易修改者否认对任何已修改的交易进行的恶意修改。并给出了PCHBA的一个实例，验证了其实用性。

正文

框架概述

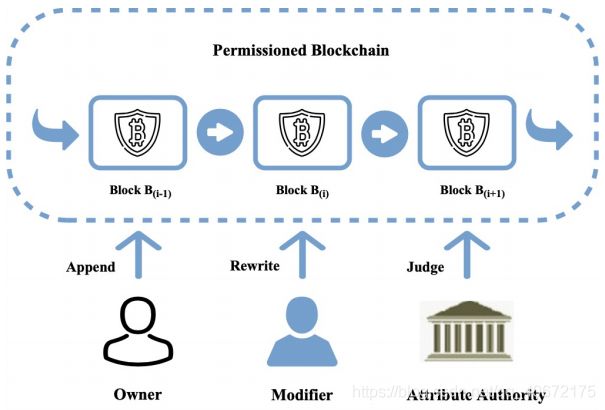
（导师箴言：打这么多字，能不能画张图啊~）
Owner：交易所有者，它将交易发布到区块链上时，对Chameleon Hash的临时后门进行加密，并使用它的签名密钥key_O在临时后门的随机版本上签名。
Attribute Authority：属性授权者，记为AA，给出Chameleon Hash的临时后门的密钥。
Modifier：消息修改者：拥有Chameleon Hash的修改权即私钥，以及AA授予的用于解密临时后门的密钥。当完成修改后，修改者还使用他的签名密钥key_M对同一个临时的后门进行随机化并在其上签名。
使用相同的临时后门来链接消息签名对：所有者-(key_O，m)，修改者-(key_M，m’)，以便实现问责。

算法步骤

交易所有者将Hash结果发送到区块链。之后，需要一个交易修改者（其修改权限由AA授予）来修改Hash对象，而Hash链的链接保持不变。如果修改后的交易发生争议，属性授权者AA可以决定修改后的交易是否确实被该交易修改者修改。
在去中心化设置方面，每个用户都可以扮演一个AA的角色，并用属性标记其他用户。我们在呈现PCHBA时使用交易“owner”和“modifier”。让一组交易修改者结合它们的修改权限来生成一个访问设备/黑盒O。
算法步骤：

• Step1：Setup（1^λ）：AA以安全参数λ为输入，输出Chameleon Hash密钥对（sk，pk）。
• Step2：KeyGen（sk，δ）：AA以Chameleon Hash的私钥sk和用户属性集δ∈U为输入，输出一个密钥sk_δ，该密钥与修改者身份ID′ 关联。U:属性宇宙
• Step3：Hash（pk，m，⋀，ID）：交易所有者执行，他以Chameleon Hash的公钥pk、消息m∈M、策略⋀和所有者身份ID作为输入，输出哈希结果h、随机数r 和签名σ。在这个过程之后，该哈希值h发布到区块链中。注意，M={0,1}*表示一般消息空间。⋀:访问结构，是U的非空子集的集合
• Step4：Verify（pk，m，h，r，σ）：以Chameleon Hash的公钥pk、消息m、哈希值h、随机数r 和签名σ作为输入，输出一个位b（0/1）。-区块链节点验证Hash的过程（“共识”）
• Step5：Adapt（sk_δ，m，m′，h，r，σ，ID′）：交易修改者执行，以密钥sk_δ，消息m和m′，哈希值h，随机数r，签名σ，修改者身份ID′ 作为输入，首先用上一步的Verify验证Hash，然后用私钥得到后门，计算可产生碰撞的r’，r’生成修改后的消息m’，生成新的公私密钥对和签名，最后发布新的Hash结果。
• Step6：Judge（sk，T，O）：给定一组交易{T′ }∈T和一组可疑交易修改者{ID′ }∈O，O:访问黑盒，如果交易T′ 链接到可疑修改者ID′，则AA输出一个交易身份对（T′，ID′），意味着交易T′ 确实被交易修改者ID′修改，其中T′=（m′，h，r′，C′，vk′，c′，σ′）。

论文认为消息拥有者和属性授权者AA是诚实可信的，对三个安全性保障：不可区分性、抗碰撞性和问责性，进行了说明。

系统模型

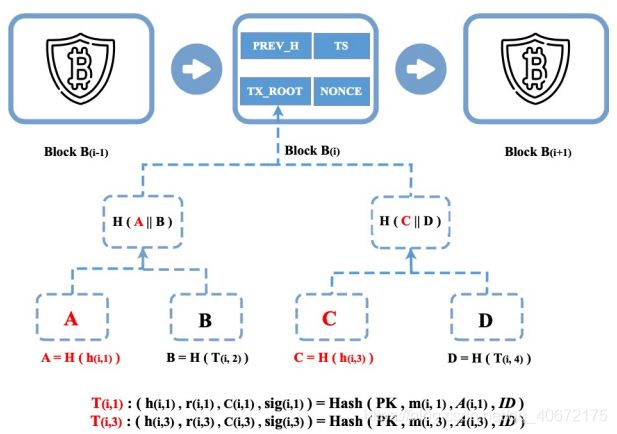
如图，区块B_(i)包含四个交易T_(i,1)，T_(i,2)，T_(i,3)，T_(i,4)，其中T_(i,1)和T_(i,3)是基于本文提出的交易，T_(i,2)和T_(i,4)使用传统的抗碰撞Hash函数H（即SHA256）进行哈希。
如果交易所有者ID希望将某些基于策略的交易发送到区块链中，则必须使用Hash（pk，m，⋀，ID）对这些交易进行哈希处理。T_(i,1)和T_(i,3)具有不同的访问策略（由交易所有者ID选择的，可执行修改的访问结构）和相同的身份（⋀_(i,1)，ID），（⋀_(i,3)，ID）。
当需要修改基于策略的交易时，具有密钥的交易修改者ID′ 可以计算Hash值A和C的有效碰撞，并提供新的随机数r’。然后，修改者向区块链网络广播新的随机数。区块链节点验证新随机数（即Verify算法）的正确性，并通过用新随机性替换旧随机数来更新区块链的本地副本。由于交易中的随机数、签名和密文 作为交易/块的非Hash部分提供，因此值PREV_H从不被修改。
如果使用PCHBA创建某些交易，我们可以确保：

• 1）不可区分性，这意味着给定一个随机性，任何公共用户都无法确定与交易T_(i,1)（或T_(i,3)）相关的随机数是使用传统哈希还是Adapt算法创建的；
• 2）抗碰撞性，这样只有具有修改权限的交易修改者ID′ 才可以修改区块链；
• 3）问责制，即如果修改后的交易存在争议，属性授权者AA可以将每个修改后的交易链接到负责的交易修改者。

三点在原文都有证明。

实现与评估

给出了一些参考算法的调整应用，以及提出的算法的具体参数设置和步骤，代码在下面的github上，在运行时间、性能、乘法和乘方的数目三方面进行了评估，这里还是看原文吧
给出的一些开源地址：

• Accenture. https://www.accenture.com/sg-en.
• Accountable Blockchain Rewriting. https://github.com/SMC-SMU/Accountable-Blockchain-Rewriting.
• BLS12-381. https://tools.ietf.org/html/draft-yonezawa-pairing-friendlycurves-02.
• General Data Protection Regulation. https://eugdpr.org.
• Hyperledger. https://www.hyperledger.org.
• Pairing-Friendly Curves. https://tools.ietf.org/id/draft-yonezawa-pairing-friendly-curves-01.html.
• Ripple. https://ripple.com.

心得

原文提出了一些定理，对它们以及算法的安全性都进行了数学上的证明，感觉自己甚至没有敲出原文精髓的百分之一，汗-_-||
第一次写csdn，写的时候关注到了一些看论文时混乱的地方，写完又加深了一遍对论文的理解，感觉尚可（公式部分就略过了等熟练了编辑器再来补。。。也可能会了也不补)
寒假实在是太混了，进度慢吞吞，本还打算下载源码研究研究，无奈刚得知周五就要汇报而我竟然只看了一篇，囧囧囧囧囧，马不停蹄奔向下一篇
特此声明，该博文所写均为本人自己理解，如有争议以论文原作者为准，（鞠躬