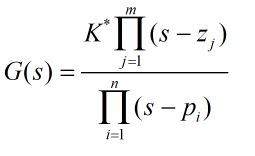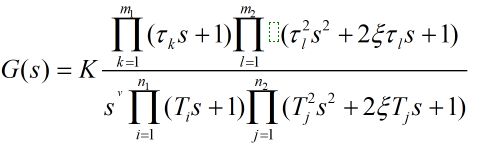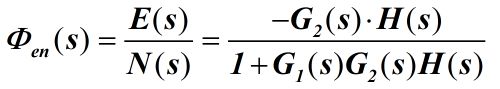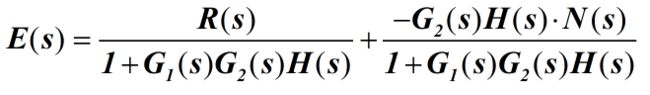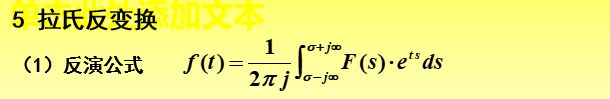自动控制原理_卢京潮_自动控制一般概念及数学模型_学习笔记

0. 自动控制原理绪论

自动控制理论是研究自动控制系统组成，进行系统分析设计的一般性理论，是研究自动控制过程共同规律的技术学科。

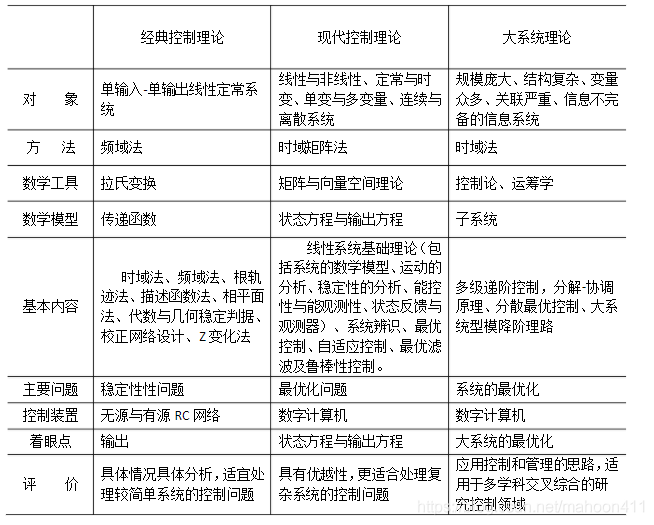
自动控制理论发展史

1. 经典控制理论
   时域法、复域法(根轨迹法)、频域法等。
   优点：可通过试验方法建立数学模型，物理概念清晰，得到广泛的工程应用。
   缺点：只适应单变量线性定常系统，对系统内部状态缺少了解，且复数域方法研究时域特性，得不到精确的结果。

2. 现代控制理论
   线性系统、最优控制、系统辨识等。
   总结：状态空间方法属于时域方法，其核心是最优化技术。它以状态空间描述（实质上是一阶微分或差分方程组）作为数学模型，利用计算机作为系统建模分析、设计乃至控制的手段。
   优点：适应于多变量、非线性、时变系统。

3. 大系统控制理论
   现代频域方法、自适应控制理论和方法、鲁棒控制方法、预测控制方法等。
   总结：大系统理论是过程控制与信息处理相结合的综合自动化理论基础，是动态的系统工程理论。它是一个多输入、多输出、多干扰、多变量的系统。

4. 智能控制理论
   专家系统、模糊控制、神经网络控制等。
   总结：智能控制的指导思想是依据人的思维方式和处理问题的技巧，解决那些目前需要人的智能才能解决的复杂的控制问题。

---

1. 自动控制的一般概念

自动控制就是：在无人直接参与下，利用控制装置，使被控对象的某一个被控量按预定的给定量运行。

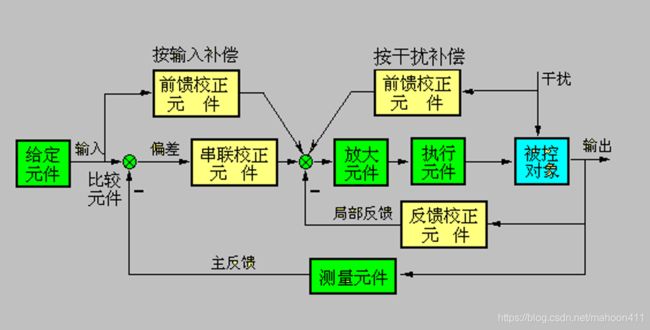
※要掌握由系统工作原理图绘制方框图的能力。

方框图的五大要素：元部件、信号及传递方向、比较点、引出点、负反馈。

基本控制方式：开环控制、闭环控制、复合控制。

• 闭环控制系统的特点：系统内部存在反馈，信号流动构成闭回路，偏差起调节作用。
• 复合控制：前馈控制+反馈控制。

负反馈原理：将系统的输出信号引回输入端，与输入信号相比较，利用所得的偏差信号进行控制，达到减小偏差、消除偏差的目的。

控制系统的组成：控制对象、控制装置。(下图的控制装置中，字体为黄颜色的装置是每个控制系统都要具备的，即测量元件、比较元件、执行机构)


控制系统的分类：

1. 按给定信号的形式： 恒值系统 / 随动(伺服)系统 / 程控系统
2. 按是否满足叠加原理：线性系统 / 非线性系统
3. 按参数是否随时间变化：定常系统 / 时变系统
4. 按信号传递的形式：连续系统 / 离散系统
5. 按输入输出变量的多少：单变量系统 / 多变量系统

对控制系统的基本要求：

1. 稳：（基本要求）
   要求系统要稳定。
2. 准：（稳态要求）
   系统响应达到稳态时，输出跟踪精度要高。
3. 快：（动态要求）
   系统阶跃响应的过渡过程要平稳， 快速。

本门(经典)自动控制原理课程的体系结构：
自动控制原理的两大任务，一个是认识系统，即分析系统，另一个是改造系统，即校正系统。认识与改造系统都是通过时域法、复域法(根轨迹法)、频域法进行的。

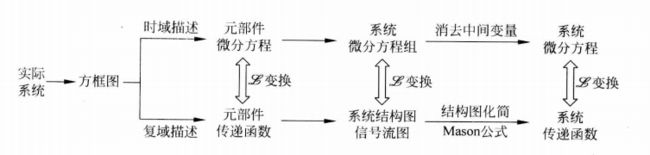
2. 控制系统的数学模型

数学模型：描述系统输入、输出变量以及内部各变量之间关系的数学表达式

建模方法：

1. 解析法（机理分析法）→适用于白盒子系统
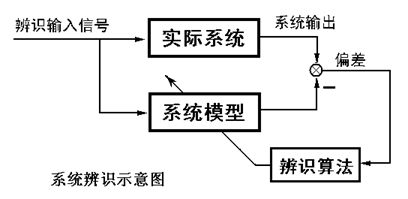
   根据系统工作所依据的物理定律列写运动方程。
2. 实验法（系统辨识法）→适用于黑盒子/灰盒子系统
   给系统施加某种测试信号，记录输出响应，并用适当的数学模型去逼近系统的输入输出特性。
   

时域模型	复域模型
微分方程	传递函数

2.1 控制系统时域数学模型

首先研究线性定常系统。

• 判断系统是不是线性的，观察输入输出变量，如果满足等式两边只有输入输出变量本身或其各阶导数，而没有常数项、交叉乘积项、变量的高阶项，那么这个系统就是线性系统。
• 判断系统是不是定常的，观察输入输出变量的系数，如果系数不随时间变化(即系数是常数)，那么这个系统就是定常系统。
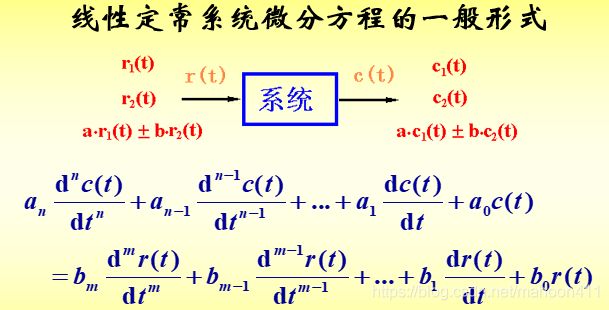
  非线性系统也可在小变化范围内线性化，然后化为线性定常系统微分方程进行求解。

借助拉普拉斯变换，可将时域微分方程化为复域代数方程进行求解，然后再借助拉氏反变换，变换到时域，最终完成对时域微分方程的求解。

但这并不是拉氏变换的主要用途，拉氏变换最主要的用途是，建立起自动控制原理中最重要的数学模型，就是系统的复域数学模型——传递函数。

2.2 控制系统复域数学模型

影响系统响应的因素有三个：

• 输入u_r(t)。规定u_r(t)为阶跃信号1(t)，这是因为阶跃信号最容易实现，比如开关，又因为阶跃信号对于一个系统来讲，是一个比较严苛的输入条件，如果这个系统跟踪阶跃信号跟踪的效果很好，那么跟踪其他信号应该问题不大。
• 初始条件。规定为零初始条件，即系统在t小于0时，系统的输入输出及它们的各阶导数均为零，因为现实中，大多数系统在接收外界激励之前，都是处于相对平衡状态的。
• 系统的结构参数。一旦输入及初始条件都统一规定之后，那么系统响应的性能指标，最终就取决于系统自身的结构参数了。即自身的特性决定了系统性能。

2.2.1 传递函数

传递函数定义：在零初始条件下，线性定常系统输出量拉氏变换与输入量拉氏变换之比。

与此同时，要注意，系统的时域数学模型：微分方程，不要求一定要在零初始条件下。因此，若题目中给出系统的传递函数，让求解此系统在非零初始条件下的响应，就需要先利用题目给出的传递函数进行拉氏反变换，求出微分方程，再将此微分方程进行拉氏变换(此时拉氏变换就要带上初始条件)进行求解。

传递函数的一般形式为；

可将一般形式的传递函数化为两类标准型：

• 首1标准型：把分子分母变量的最高次幂的系数提出来，写成K^*，即可化为首1标准型。注意要保证变量s的系数是正值。
  

• 尾1标准型：把分子分母的尾项都提取出来，保证尾项为1，提取出的常数项相乘后写成K，即可化为尾1标准型。注意要保证变量s的系数是正值。
  尾1标准型中的K叫做增益。
  

传递函数的性质：

1. G(s)是复函数；
2. G(s)只与系统自身的结构参数有关；
3. G(s)与系统微分方程直接关联；
4. G(s) = L[ k(t) ]；
   其中k(t)为系统的单位脉冲响应，即系统的传递函数与系统的单位脉冲响应互为拉氏变换对。
5. G(s) 与 s 平面上的零极点图相对应。
   s平面即自变量s的取值范围。G(s)的分子多项式对应的根叫做系统的零点，分母多项式对应的根叫做系统的极点。
   因此由G(s)可绘制零极点图，由零极点图也可还原出不包含K^*的G(s)。

传递函数的局限性：

1. 原则上不反映非零初始条件时系统响应的全部信息；
   因为传递函数是建立在零初始条件下的。但如果想求非零初始条件时系统响应的信息也可以求得：把传递函数进行拉氏反变化，变换为微分方程，然后再把微分方程通过拉氏变换(代入初始条件)进行求解。
2. 适合于描述单输入/单输出系统；
   由传递函数的定义可知，传递函数只能是一个输出的拉氏变换对一个输入的拉氏变换的比值。
3. 只能用于表示线性定常系统。
   因为系统如果是非线性或者时变的话，那么虽然可以求得微分方程的拉氏变换，但无法导出C(s)/R(s)，即无法定义系统的传递函数。

2.2.2 典型环节

自动控制系统中的元部件有很多种，比如机械、电气、化工、航空航天等许多领域的元部件，工作原理都不相同。但可以将它们对应的传递函数抽象出来，它们可能有相同形式的传递函数。环节指的就是具有相同形式传递函数的元部件的分类。将环节再次抽象，即为典型环节。
典型环节：由元部件抽象出来的传递函数可以看成是有限个基本单元的组合。这些基本单元就称为典型环节。

• 不同的元部件可以有相同的传递函数。
• 若输入输出变量选择不同，同一部件可能有不同的传递函数。
• 任一传递函数都可看做典型环节的组合。

下图列出了所有典型环节。

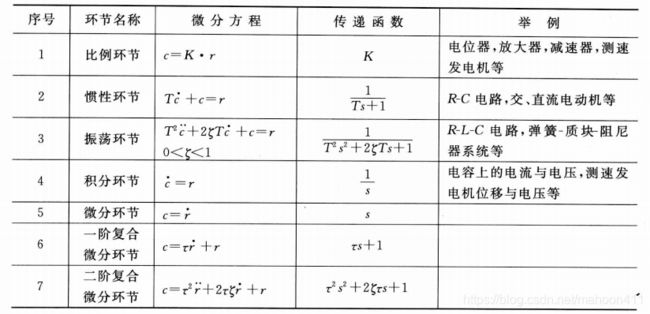
需要注意的是：实际中的系统都是因果系统，都具有惯性，只有给系统输入信号之后，系统才会产生输出。因此，这种系统抽象出来的传递函数，一般都是分母的阶数高于分子的阶数。因此上面列出的七个典型环节中，后三个微分环节，没有实际的物理系统与之对应。

并且在建立系统传递函数时，还需要注意负载效应。一定要在系统能够正常工作的环境下，来建立系统的传递函数。

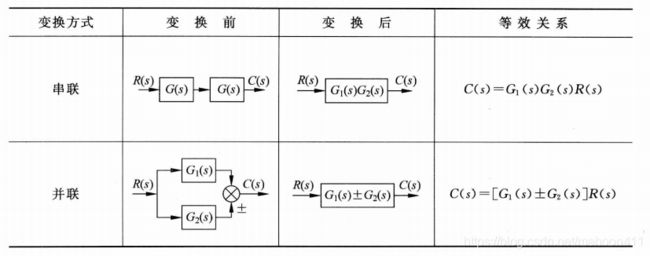
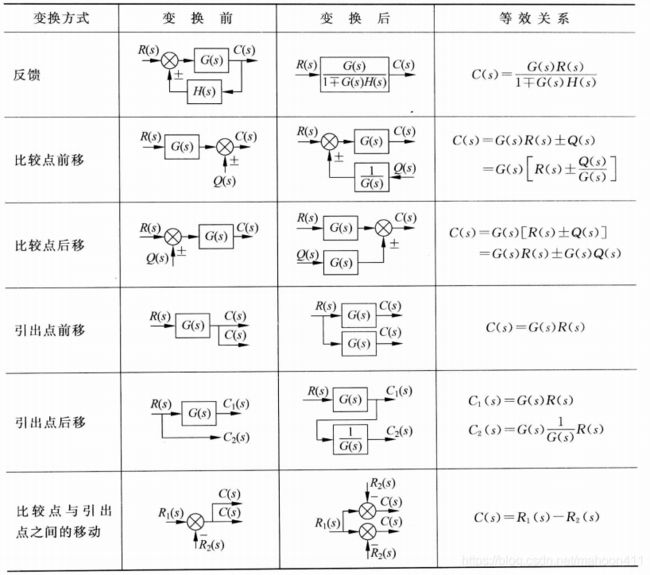
2.3 控制系统的结构图及其等效变换

2.3.1 结构图等效变换规则

2.4 控制系统的信号流图

掌握结构图和信号流图的相互转换。

Mason增益公式：


总体来讲，系统模型及其建立过程如下图所示。

2.5 控制系统的传递函数

说明一下，系统的开环传递函数一般用G(s)表示，闭环传递函数一般用Φ(s)表示。

2.5.1 开环传递函数

首先要注意的是，开环传递函数指的不是开环系统的传递函数，开环传递函数是针对闭环系统而言的。
开环传递函数是把闭环系统的主反馈通路打断，将前向通路与反馈通路上的传递函数乘到一起。


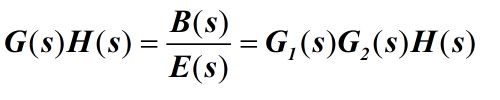
把开环传递函数化为尾1标准型，得到的常数项K称为开环增益。

还是以上述系统为例，定义此系统的闭环传递函数有四种：
输入R(s)对输出C(s)，输入R(s)对偏差E(s)，扰动N(s)对输出C(s)，扰动N(s)对偏差E(s)。

2.5.2 输入R(s)作用下的闭环传递函数

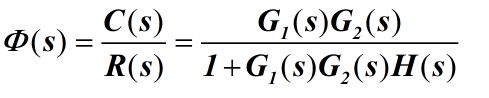
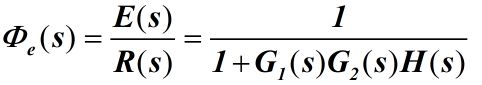
注意到，分母有一部分就是系统的开环传递函数。即，分母是1+开环传递函数。

2.5.3 扰动N(s)作用下的误差传递函数

2.5.4 系统的总输出C(s)及总误差E(s)

3. 附录：拉普拉斯变换

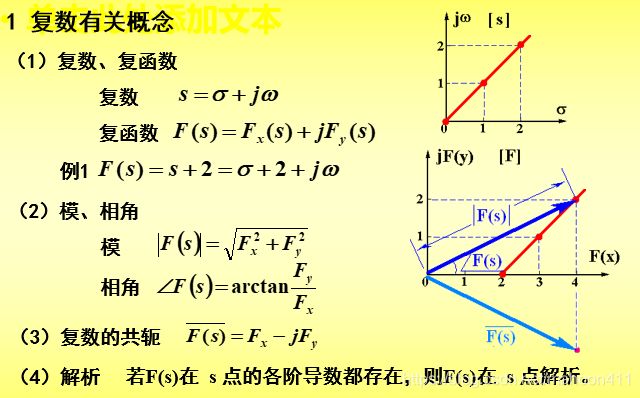
3.1 复数与复函数

对于复函数来说，其自变量为复数s，需要用一个二维复平面(s平面)去表述；因变量为F(s)，也是复数，同样需要一个二维复平面(F平面)去表述。
因此完整描述一个复函数，需要两个二维复平面(s平面和F平面)去表述。如下图两个红线所示
复函数的模如下图蓝线所示，其对应的相角如下图所示。

3.2 拉氏变换

微分定理中，可以把复域s·F(s)中前面的s类比到时域中f(t)的一个微分算子d，即df(t)→s·F(s)。

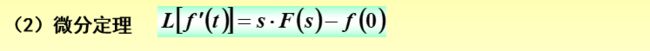
那么对时域中的f(t)求n阶导，相当于在复域中对F(s)乘n个s，再减去一系列的初始条件，包括初始位置、初始速度、初始加速度等等。若f(t)初条件都为0，则其拉氏变换为sⁿF(s)。




实位移定理与复位移定理的综合应用例题：先应用实位移定理，再应用复位移定理。

初值定理用于只知道象函数F(s)，而不知道原象f(t)，又要计算f(t)的初值的情况。

终值定理通常用来计算系统的稳态误差。

3.3 拉氏反变换

但是一般来说，应用反演公式去求拉氏反变化比较困难。

因此实际应用中，通常使用查表法去求解拉氏反变换。即先把F(s)拆分成表中存在的常见函数的形式，再按照表进行拉氏反变换。

把F(s)拆分的过程就叫做分解部分分式法，可以通过试凑法、系数比较法、留数法进行实现。常用的是留数法。拉氏反变换的难点也在于如何把F(s)分解为部分分式。

3.3.1 模态(振型)

例如有一个四阶系统。

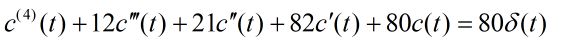
将其进行求解得到系统单位脉冲响应c(t)为：

(系统响应即是系统的模态的线性组合)
可以看出，此系统的四个模态分别为e^-2t，e^-8t，e^-tsin2t，e^-tcos2t。

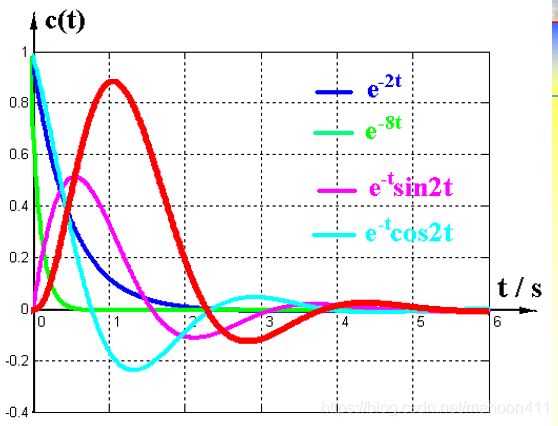
此系统最终的响应就是这四个模态通过不同权值进行叠加后得到的。

3.3.2 留数法分解部分分式

注意使用留数法的前提是，F(s)一定要是有理真分式，即n>m。


上述公式记忆起来比较困难，因此也采用如下方法进行留数的求解：
如下图所示，先在等式两边同时乘以(s-p₁)^m,这时候观察等式右边可知，除了C_m项，其余各项都含有(s-p₁)这一项。因此令等式两边的s等于p₁，等式右边就只剩下了C_m项，等式左边就变成了求极限的一个式子。这时求出等式左边的极限，C_m就求出来了。
接着求C_m-1，还是先在原等式两边同时乘以(s-p₁)^m，然后再对等式两边求一次导数，这样等式右边的C_m就被消去，而C_m-1就变为常数项了，接下来用求C_m的方法就可以求出C_m-1了。
同理，可以求出所有的留数。