数学建模之pearson、spearman相关系数
相关系数
用来衡量两个变量之间 的相关性大小。
根据数据满足的不同条件,选择不同的相关系数来计算分析。
总体和样本
总体:考察对象的全部个体
样本:从总体数据中抽取一部分个体
皮尔逊pearson相关系数(线性+近似正态分布)
注意:只是用来衡量两个变量线性相关程度,在说明相关性时,必须绘制散点图,加上该系数的值才能说明相关性的程度,原因如下:
(1)非线性相关也可能导致pearson相关系数很大
(2)离群点对pearson相关系数的影响很大
(3)即便是pearson相关系数为0,只能说不是线性相关,但有可能存在更复杂的相关性
总体Pearson相关系数
若两组数据为X:{X1,X2,X3,…,Xn}和Y:{Y1,Y2,Y3,…,Yn}
总体均值:
E ( X ) = ∑ i = 1 n X i n , E ( Y ) = ∑ i = 1 n Y i n E(X)=\frac{\sum_{i=1}^{n}{X_i}}{n}\ ,\ \ E(Y)=\frac{\sum_{i=1}^{n}{Y_i}}{n} E(X)=n∑i=1nXi , E(Y)=n∑i=1nYi
总体协方差:
C o v a r ( X , Y ) = ∑ i = 1 n ( X i − E ( X ) ) ( Y i − E ( Y ) ) n Covar(X,Y)=\frac{\sum_{i=1}^{n}{(X_i-E(X))(Y_i-E(Y))}}{n} Covar(X,Y)=n∑i=1n(Xi−E(X))(Yi−E(Y))
协方差:
若X,Y的变化方向相同,则协方差为正,反之则为负
注:协方差的大小与两个变量的量纲密切相关,故其大小不适合作比较。
σ标准差:
σ X = ∑ i = 1 t ( X i − E ( X ) ) 2 n σ Y = ∑ i = 1 t ( Y i − E ( Y ) ) 2 n \sigma_X=\sqrt{\frac{\sum_{i=1}^{t}{(X_i-E(X))^2}}{n}}\\ \sigma_Y=\sqrt{\frac{\sum_{i=1}^{t}{(Y_i-E(Y))^2}}{n}} σX=n∑i=1t(Xi−E(X))2σY=n∑i=1t(Yi−E(Y))2
总体Pearson相关系数:
ρ X Y = C o v a r ( X , Y ) σ X σ Y = ∑ i = 1 t ( X i − E ( X ) ) 2 σ X ( Y i − E ( Y ) ) 2 σ Y n ρ_{XY}=\frac{Covar(X,Y)}{\sigma_X\sigma_Y}=\frac{\sum_{i=1}^{t}{\frac{(X_i-E(X))^2}{\sigma_X}\frac{(Y_i-E(Y))^2}{\sigma_Y}}}{n} ρXY=σXσYCovar(X,Y)=n∑i=1tσX(Xi−E(X))2σY(Yi−E(Y))2
该相关系数剔除了两个变量量纲的影响,即标准化后的协方差
Pearson相关系数的性质:
∣ ρ X Y ∣ ≤ 1 , 且 当 Y = a X + b , ρ X Y = { 1 , a > 0 − 1 , a < 0 |ρ_{XY}|≤1\ ,且当Y=aX+b\ ,ρ_{XY}=\begin{cases} 1\ &,a>0\\ -1\ &,a<0 \end{cases} ∣ρXY∣≤1 ,且当Y=aX+b ,ρXY={ 1 −1 ,a>0,a<0
证明:
∣ ρ X Y ∣ ≤ 1 |ρ_{XY}|≤1 ∣ρXY∣≤1
证:
1 、 先 构 造 a + b X 和 Y 的 均 方 误 差 的 期 望 E { [ Y − ( a + b X ) ] 2 } = E ( Y 2 ) + b 2 E ( X 2 ) + a 2 − 2 b E ( X Y ) + 2 a b E ( X ) − 2 a E ( Y ) 1、先构造a+bX和Y的均方误差的期望\\ E\{[Y-(a+bX)]^2\}=E(Y^2)+b^2E(X^2)+a^2-2bE(XY)+2abE(X)-2aE(Y)\\ 1、先构造a+bX和Y的均方误差的期望E{ [Y−(a+bX)]2}=E(Y2)+b2E(X2)+a2−2bE(XY)+2abE(X)−2aE(Y)
2 、 求 出 该 期 望 的 最 小 值 为 ( 1 − ρ X Y 2 ) D ( Y ) 2、求出该期望的最小值为(1-ρ_{XY}^2)D(Y)\\ 2、求出该期望的最小值为(1−ρXY2)D(Y)
3 、 由 于 均 方 误 差 和 方 差 均 ≥ 0 , 且 m i n E { [ Y − ( a + b X ) ] 2 } = ( 1 − ρ x y 2 ) D ( Y ) 3、由于均方误差和方差均≥0,且\\ minE\{[Y-(a+bX)]^2\}=(1-ρ_{xy}^2)D(Y)\\ 3、由于均方误差和方差均≥0,且minE{ [Y−(a+bX)]2}=(1−ρxy2)D(Y)
故 ( 1 − ρ X Y 2 ) ≥ 0 , 所 以 ∣ ρ X Y ∣ ≤ 1 故(1-ρ_{XY}^2)≥0,所以|ρ_{XY}|≤1 故(1−ρXY2)≥0,所以∣ρXY∣≤1
| 相关性 | 负 | 正 |
|---|---|---|
| 无相关性 | -0.10 ~ 0.0 | 0.00 ~ 0.10 |
| 弱相关性 | -0.30 ~ -0.10 | 0.10 ~ 0.30 |
| 中相关性 | -0.50 ~ -0.30 | 0.30 ~ 0.50 |
| 强相关性 | -1.00 ~ -0.50 | 0.50 ~ 1.00 |
上表仅供参考,具体范围由具体情况而定。
如下截取的5张图片来自于清风老师课程的讲义PPT~
使用SPSS软件能够更简单的绘制描述性统计以及矩阵散点图
clc,clear;
load 'grils'' physical fitness test.mat' % 文件名有空格时,必须加引号,有引号时,多加一个引号
% 统计描述
A_MIN = min(A);
A_MAX = max(A);
A_MEAN = mean(A);
A_MEDIAN = median(A);
A_SKEWNESS = skewness(A);
A_KURTOSIS = kurtosis(A);
A_STD = std(A);
ALL_RESULT = [A_MIN;A_MAX;A_MEAN;A_MEDIAN;A_SKEWNESS;A_KURTOSIS;A_STD];
% 计算各列(指标)之间的相关系数
% 在计算之前一定要绘制散点图,看两组变量之间是否存在线性关系
% 此时使用SPSS软件比较方便——图形-》旧对话框-》散点图/点图-》矩阵散点图
R = corrcoef(A)
R =
1.0000 0.0665 -0.2177 -0.1920 0.0440 0.0951
0.0665 1.0000 0.0954 0.0685 0.0279 -0.0161
-0.2177 0.0954 1.0000 0.2898 0.0248 -0.0749
-0.1920 0.0685 0.2898 1.0000 -0.0587 -0.0019
0.0440 0.0279 0.0248 -0.0587 1.0000 -0.0174
0.0951 -0.0161 -0.0749 -0.0019 -0.0174 1.0000
Pearson相关系数假设性检验
该假设检验的条件为:
- 实验数据通常假设是成对的来自于***正态分布*** 的总体(t检验是基于数据呈正态分布假设的)
- 实验数据之间的差距不能过大,否则对peason相关系数影响极大
- 每组样本之间是独立抽样的
拒绝原假设意味着pearson相关系数显著异于0
论文中的相关系数为0.5、0.5*、0.5**、 0.5*** (显著性标记)
分别代表不显著异于0, 在90%的置信水平上异于0,在95%的置信水平上异于0,在99%的置信水平上异于0
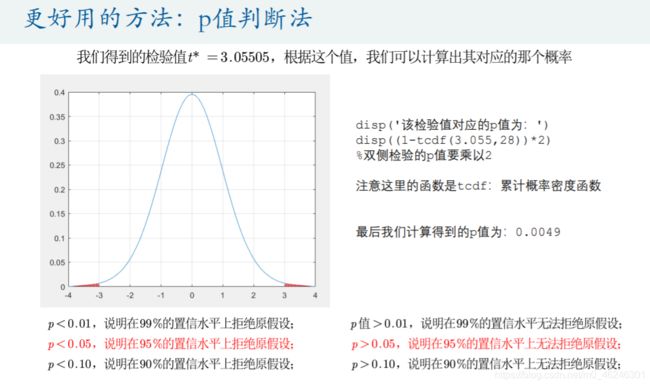
% Pearson相关系数假设性检验
x = -4:0.1:4;
y = tpdf(x,28); % 求t分布的概率密度值,28位自由度
figure(1)
plot(x,y,'-')
grid on
hold on
% 求出临界值
tinv(0.975,28) % 0.975=0.95+0.025
% 利用累计密度函数cdf的反函数
plot([-2.048,-2.048],[0,tpdf(-2.048,28)],'r-')
plot([2.048,2.048],[0,tpdf(-2.048,28)],'r-')
% 计算P值
[R,P] = corrcoef(A)
% 可直接在EXCEL中手动进行显著性标记
disp('1表示在99%的置信水平上拒绝原假设:')
P<0.01
disp('1表示在95%的置信水平上拒绝原假设:')
(P<0.05).*(P>0.01)
disp('1表示在90%的置信水平上拒绝原假设:')
(P<0.1).*(P>0.05)
% 若数据量过大,在SPSS中操作
正态分布假设性检验
[H,P] = jbtest(X,alpha)
- H为测试结果,若H为0,则认为近似服从正态分布;若H为1,则认为不近似服从正态分布。
- P为接受假设的概率,小于alpha则可以拒绝近似正态分布的假设
- X为传入的矩阵
- alpha为0.05代表在95%的置信水平上
% 正态分布检验
% 正态分布的偏度和峰度
x = normrnd(2,3,10000,1);
SKEWNESS = skewness(x) % 偏度
KURTOSIS = kurtosis(x) % 峰度
qqplot(x) % 若近似在一条直线上,说明近似为正态分布(要求数据量特别大)
% 检验第一列数据是否正态分布
[h,p] = jbtest(A(:,1),0.05) % 只能传入向量,95%的置信水平
% 循环JB检验所有列的数据——适用于大样本
n_A = size(A,2)
H = zeros(1,6); % 初始化:节省时间和消耗
P = zeros(1,6);
for i = 1:n_A
[H(i),P(i)] = jbtest(A(:,i),0.05);
end
disp(H)
disp(P)
% 1 1 1 1 1 1
% 0.0110 0.0010 0.0136 0.0010 0.0010 0.0393
% 均小于0.05,故均拒绝原假设
% 说明在95%的置信水平上,不近似满足正态分布,故不能使用pearson相关系数
斯皮尔曼spearman等级相关系数
Example:
clc,clear;
load 'boys''test.mat'
% 1、JB检测法检测是否近似正态分布
% 循环所有列(指标)的数据
n_B = size(B,2);
H = zeros(1,n_B); % 初始化:节省时间和消耗
P = zeros(1,n_B);
for i=1:n_B
[H(i),P(i)] = jbtest(B(:,i),0.05); % 1代表不满足近似正态分布,0代表满足。
end
disp(H)
disp(P)
% 2、qq图
% 若近似在一条直线上,说明近似正态分布
for i=1:n_B
qqplot(B(:,i))
end
% 3、绘制散点图(SPSS软件)
% 由1、2、3得知该六个指标均不近似满足正态分布,所以不能使用pearson相关系数,故使用spearman相关系数
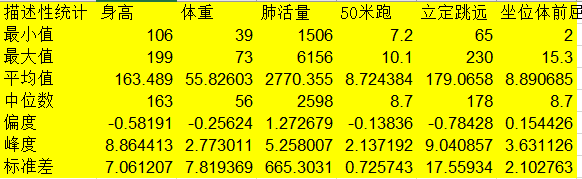
% 4、统计描述
B_MIN = min(B);
B_MAX = max(B);
B_MEAN = mean(B);
B_MEDIAN = median(B);
B_SKEWNESS = skewness(B);
B_KURTOSIS = kurtosis(B);
B_STD = std(B);
ALL_RESULT = [B_MIN;B_MAX;B_MEAN;B_MEDIAN;B_SKEWNESS;B_KURTOSIS;B_STD]
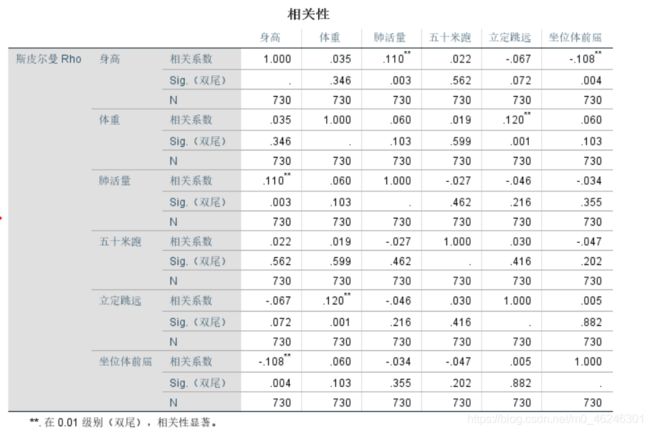
% 5、spearman相关系数以及p值
[R_spearman,P] = corr(B,'type','Spearman')
% 6、由相关系数对应到相关性,以及p值进行假设检验
% p<0.01,说明在99%的置信水平上拒绝原假设 ***
% p<0.05,说明在95%的置信水平上拒绝原假设 **
% p<0.10,说明在90%的置信水平上拒绝原假设 *
% 本例中,拒绝原假设意味着spearman相关系数显著异于0
1 1 1 1 1 1
0.0010 0.0129 0.0010 0.0010 0.0010 0.0029
| 相关性 | 负 | 正 |
|---|---|---|
| 无相关性 | -0.10 ~ 0.0 | 0.00 ~ 0.10 |
| 弱相关性 | -0.30 ~ -0.10 | 0.10 ~ 0.30 |
| 中相关性 | -0.50 ~ -0.30 | 0.30 ~ 0.50 |
| 强相关性 | -1.00 ~ -0.50 | 0.50 ~ 1.00 |
散点图:
QQ图:
Spearman第一种实现:
相同的数值在它们的位置取算数平均
Spearman_1.m函数
function [R, P] = Spearman_1(X, kind)
% X为m*n数据矩阵; kind: 1表示单侧检验 2表示双侧检验
[m,n] = size(X);
%%%%% 1、判断用户输入的参数,若只输入X则默认kind=2
if nargin == 1
kind = 2;
end
%%%%% 2、判断是否合法
if n<2
%disp('指标过少,不能用于计算')
elseif m<30
disp('样本个数过少,可直接插临界值表进行假设检验')
elseif kind~=1 && kind~=2
disp('kind只能输入1/2')
else
%%%%% 3、计算R和P
R = ones(n);
P = ones(n);
for i = 1:n
for j = (i+1):n
% 计算R矩阵
Rank_X = rank_X(X(:,i)); % 保证相同的数值在它们的位置取算数平均
Rank_Y = rank_X(X(:,j));
d_ij = Rank_X - Rank_Y; % 两列的等级差
R(i,j) = 1 - (6 * sum(d_ij.*d_ij))/(m*(m^2-1)); % 带公式计算
R(j,i) = R(i,j); % 对角相等
% 计算P矩阵
P(i,j) = (1-normcdf((abs(R(i,j)*sqrt(m-1)))))*kind; % *(1/2)区别单侧和双侧检验
P(j,i) = (1-normcdf((abs(R(j,i)*sqrt(m-1)))))*kind;
end
end
end
rank_X.m函数
function [Rank_X] = rank_X(X_col)
% 保证相同的数值在它们的位置取算数平均
[~,Index_X] = sort(X_col); % [5 10 9 10 6]'--> [1 5 3 2 4]'
[~,Rank_X] = sort(Index_X); % [1 5 3 2 4]'--> [1 4 3 5 2]'
for i = 1:size(X_col,1)
pos = (X_col == X_col(i)); % 如[5 10 9 10 6]',当i=2/4时对应pos为[0 1 0 1 0]'
Rank_X(pos == 1) = sum(Rank_X.*pos) / sum(pos); % [1 4.5 3 4.5 2]'
end
end
参考资料:数学建模清风:论文写作方法课程 https://www.bilibili.com/video/BV1Na411w7c2