并查集的总结（数量+加权+扩展域+例题+萌新求赞）

并查集大总结（萌新表示很难过，看了好久的这东东(；′⌒`)）

                                                                                南昌理工ACM

---

• 什么是并查集呢
  简单的讲就是合并集合和查找集合（非常好用）
  并查集适合维护具有非常强烈的传递性质,或者是连通集合性质.

• 并查集的性质

  1 传递性
  2 连通性
  简单来说就是 亲戚的亲戚就是我的亲戚 朋友的朋友就是我的朋友
  （并查集的经典语句 哈哈 ）

---

并查集属于半模板数据结构
可以有很多种维护方式（后面我会举几个，我刚学一些，也不是很懂，萌新磕头）

先说并查集怎么用

• 并查集的初始化，开始时全部的数字，各自为一个集合

for(int i=1;i<=n;i++) p[i]=i;///初始化,就是这么简单

• 并查集的合并

再讲合并之前我们要讲一下路径压缩

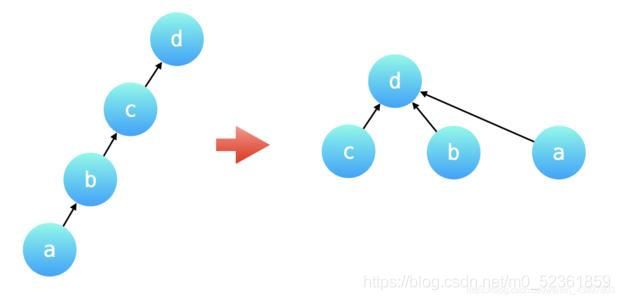
如图，就是将所以的点全部连到了他的最上面的节点，主要是为了减少查找时间（高效）
代码如下

int find(int x){
     
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}

这就是俗称 找爸爸函数 （字面意思）

合并两个集合，很容易，只要把他的祖宗节点并到另一个集合就行
查找两个集合，就是看看他们有没有在一个集合里，就行。

int find(int x){
     
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}

p[find(a)]=find(b);//合并集合

if(find(a)==find(b)) puts("Yes");//查找集合
else puts("No");

这些就是整个并查集的核心（但这不是全部，这是半模板的数据结构）
剩下的主要靠你自己维护（下面介绍几个比较好的并查集类型）
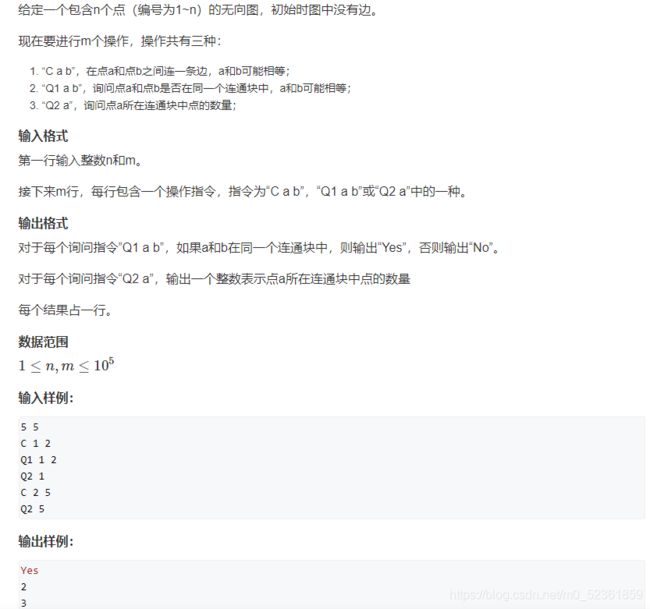
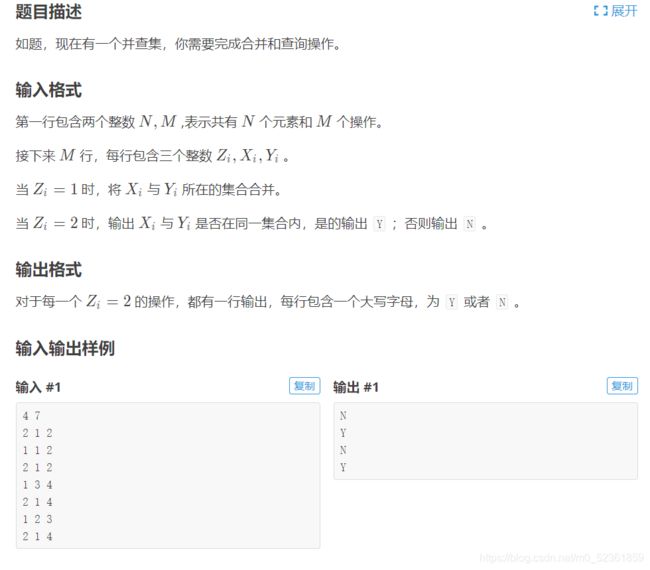
这里先练一道模板题

代码如下

#include
#include
using namespace std;
const int N=2e5+10;
int p[N];
int n,m;
int find(int x){
     
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}
int main(){
     
    cin>>n>>m;
    for(int i=1;i<=n;i++) p[i]=i;
    while(m--){
     
        int a,b,c;
        cin>>a>>b>>c;
        if(a==1) p[find(b)]=find(c);
        else{
     
            if(find(b)==find(c)) puts("Y");
            else puts("N");
        }
    }
    return 0;
}

---

重点来了

- 并查集主要维护 有三
1 数量
2 种类
3 权重

在学习这三种之前我们看一道（关于反集思想的并查集，来感受一下并查集的魅力）
反集主要应用 就一句话
敌人的敌人就是朋友（伙伴们来题）

超经典 点开看看吧

代码如下

#include
#include
using namespace std;
const int N=1010;
int n,m,p[N*2];
int find(int x){
     
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}
int main(){
     
    cin>>n>>m;
    for(int i=1;i<=2*n;i++) p[i]=i;
    for(;m;m--){
     
        char op[2];
        int a,b;
        scanf("%s%d%d",op,&a,&b);
        if(*op=='F'){
     
            p[find(a)]=find(b);
        }
        else{
     
            p[find(a+n)]=find(b);
            p[find(b+n)]=find(a);   //反集合并
        }
    }
    int ans=0;
    for(int i=1;i<=n;i++)
        if(p[i]==i) ans++;
    cout<<ans;
    return 0;
}

主要思想就是反集（将敌人的敌人变成朋友 0.0）

大家在纸上画一下就明白了
通过交替的反集思想来解决问题
是不是感觉到并查集 的强大
反正我是对这个东西，佩服的五体投地，被虐的太惨 /(ㄒoㄒ)/~~

---

数量并查集的维护

这里我推荐ACwing这道新手题

代码如下

#include

using namespace std;
const int N=1e5+10;
int p[N],sz[N];
int n,m,a,b;
string str;
void init(){
     
    for(int i=1;i<=n;i++){
     
        p[i]=i;
        sz[i]=1;
    }
}
int find(int x){
     
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}
void merge(int a,int b){
     
    int x=find(a);
    int y=find(b);
    p[x]=y;
    sz[y]+=sz[x];
}
int main(){
     
    cin>>n>>m;
    init();
    while(m--){
     
        cin>>str;
        if(str=="C"){
     
            cin>>a>>b;
            if(find(a)!=find(b)) merge(a,b);
        }
        else if(str=="Q1"){
     
            cin>>a>>b;
            if(find(a)==find(b)) puts("Yes");
            else puts("No");
        }
        else {
     
            cin>>a;
            cout<<sz[find(a)]<<endl;
        }
    }
    return 0;
}

这里主要是维护根节点的大小，不进行子节点不需要维护
所以只需要更新根节点的sz数组就行了（size打不出来，就用sz了）
这种题型也比较常见，无非是换了一种写法，相信大家可以认真对待

难搞的并查集来了

---

• 扩展域并查集和加权并查集

这里我们一起讲
用最经典的食物链吧，方便理解
食物链题目 请点击
这里先上代码

• 扩展域做法

#include

using namespace std;
const int N=5e4+10;
int p[N*3];
int n,m,ans;
int find(int x){
     
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}
int main(){
     
    cin>>n>>m;
    for(int i=1;i<=3*n;i++) p[i]=i;
    for(;m;m--){
     
        int op,x,y;
        cin>>op>>x>>y;
        if(x>n||y>n) ans++;
        else if(op==1){
     
            if(find(x)==find(y+n)||find(x+n)==find(y)) ans++;
            else{
     
                p[find(x)]=find(y);
                p[find(x+n)]=find(y+n);
                p[find(x+n+n)]=find(y+n+n);
            }
        }
        else{
     
            if(find(x)==find(y)||find(x)==find(y+n)) ans++;
            else{
     
                p[find(x+n)]=find(y);
                p[find(x+n+n)]=find(y+n);
                p[find(x)]=find(y+n+n);
            }
        }
    }
    cout<<ans;
    return 0;
}

• 加权做法

#include
#include
using namespace std;
const int N=5e4+10;
int p[N],r[N];
int n,m,ans;
int find(int x){
     
    if(p[x]!=x){
     
        int t=p[x];
        p[x]=find(p[x]);
        r[x]+=r[t];
    }
    return p[x];
}
int main(){
     
    cin>>n>>m;
    for(int i=1;i<=n;i++) p[i]=i;
    for(;m;m--){
     
        int op,a,b;
        scanf("%d%d%d",&op,&a,&b);
        if(a>n||b>n) ans++;
        else if(op==2&&a==b) ans++;
        else{
     
            op--;
            int x=find(a);
            int y=find(b);
            if(x==y){
     
                if((((r[a]-r[b])%3)+3)%3!=op) ans++;
            }
            else{
     
                p[x]=y;
                r[x]=r[b]-r[a]+op;
            }
        }
    }
    cout<<ans;
    return 0;
}

这里我给出两种方法的详解
这里，详细的讲解了加权并查集

---

秦大佬 的讲解 我觉得最好 关于扩展域并查集

---

最后附上一个简单题，让大家轻松一下

简单题 这里我用的是tried树+并查集

#include
#include
using namespace std;
const int N=2e5+10;
int p[N];
int son[N][58],cut[N],idx;
int n,m;
int find(int x){
     
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}
void insert(string a,int k){
     
    int p=0;
    for(int i=0;i<a.size();i++){
     
        int u=a[i]-'A';
        if(!son[p][u]) son[p][u]=++idx;
        p=son[p][u];
    }
    cut[p]=k;
}
int query(string a){
     
    int p=0;
    for(int i=0;i<a.size();i++){
     
        int u=a[i]-'A';
        p=son[p][u];
    }
    return cut[p];
}
int main(){
     
    cin>>n>>m;
    for(int i=1;i<=n;i++){
     
        p[i]=i;
        string a;
        cin>>a;
        insert(a,i);
    }
    for(;m;m--){
     
        string a,b;
        cin>>a>>b;
        p[find(query(a))]=find(query(b));
    }
    cin>>n;
    for(;n;n--){
     
        string a,b;
        cin>>a>>b;
        if(find(query(a))==find(query(b))) puts("Yes.");
        else puts("No.");
    }
    return 0;
}

这是我的小小总结，希望大家能多多加油
萌新的我，才刚刚接触代码不久，路是那么那么远
想想就伤心 ，算法没有尽头啊
哭泣/(ㄒoㄒ)/~~
支持我一下下吧，希望得到大家的点赞
制作不易，谢谢大家