python3 动态规划 数组 最长连续递增子序列

题目链接

https://leetcode-cn.com/problems/longest-continuous-increasing-subsequence/

题目介绍

---

最长连续递增序列
给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。

示例 1：

输入：nums = [1,3,5,4,7]

输出：3

解释：最长连续递增序列是 [1,3,5], 长度为3。

尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被
4 隔开。

---

Dynamic Programming

---

class Solution:
    def findLengthOfLCIS(self, nums: List[int]) -> int:
        n = len(nums)
        # 初始化
        dp = [1] * n
        if not nums:
            return 0
        for i in range(1, n):
            if nums[i] > nums[i - 1]:
                dp[i] = dp[i - 1] + 1
        return max(dp)

思路

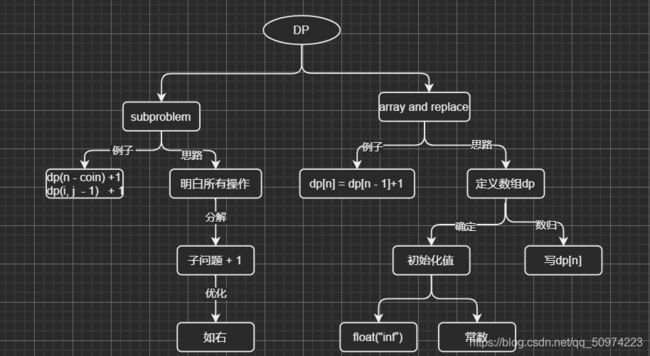
很多时候，感觉是可以用DP去做的，一开始基例还行，到状态转移方程这就没有状态了，继而导致这一道题卡住。接下来，讲一下，动态规划的一般步骤

在本题显然把它分为子问题去做泡汤了，因为它要进行的操作并不明显。所以采用 array and replace

定义

dp数组的定义是至关重要的一步，这里我们定义为nums数组到nums[i](包含)的最大子序列长度

举个例子，比如 nums = [1,3,5,4,7],那么dp[3] = 3

初始值

最坏的情况是第二个就小于第一个，那么只有第一个，所以初始值均为1

数归求通项

如果递增，是不是就等于前一个加一呢，那么，读者有疑惑的地方在于如果中间递减了呢，那么不加任何操作。它初始还是1，后面递增，再加上去。最后直接求max(dp),轻轻松松。

注意点

本题nums可为空，所以有了一开始if的判断

然后如果一开始直接判断成功return值，后面的语句即便是可执行也会一概不看

---

滚动窗口

一般来说，子序列问题都可以用滚动窗口以及双指针的方法做

class Solution:
    def findLengthOfLCIS(self, nums: List[int]) -> int:
        ans, anchor = 0, 0
        n = len(nums)
        for i in range(n):
            if i and nums[i] <= nums[i - 1]:
                anchor = i
            ans = max(ans, i - anchor + 1)
        return ans

思路

如果乖乖递增，anchor为0，等于没有，那么i + 1即为长度

如果出现递减现象，那么anchor = i减一下变为0，长度为1，可以比喻为从当前地方重新开始

同样的，本题采用了自对抗的方式，首先设置一个answer = 0然后不断取最大

注意点

之所以这个方法没有像之前的设置判断语句，是因为就算整个for控制的结构失效了，ans的初始值还是为0

另外，有读者说了，for遍历我设置成(1,n)不也一样嘛，

但是请读者想一下如果nums = [1]呢，改了之后整个结构失效，但是解法好就好在只会失效个if判断

双指针

class Solution:
    def findLengthOfLCIS(self, nums: List[int]) -> int:
        n = len(nums)
        if not nums:
            return 0
        tem_res = 1
        res = 0
        for i in range(1, n):
            if nums[i] > nums[i - 1]:
                tem_res += 1
            else:
                res = max(res, tem_res)
                tem_res = 1
        return max(res, tem_res)

思路

这道题一开始用这种方法棘手的原因在于，碰到边界就要重置，但是前面万一一直递增结果怎么办？

这种解法就提供了一个好的方法：

一个暂时的结果，一个是结果

如果递增，暂时结果不断加1

如果开始递减，赶快把前面递增的成果保留到res里面，然后从容地重置为1

注意点

最后不能直接return res,万一后面增的更厉害呢，所以还要对抗一下

拓展

子序列问题可以用双指针和滚动窗口

大家觉得写的好的可以去github给我点个小星星呀
https://github.com/sherlcok314159/leetcode-python-3/blob/main/md/sub.md