数据结构与算法--哈夫曼树/赫夫曼树 Python实现哈夫曼树 Python实现赫夫曼树 哈夫曼编码 哈夫曼压缩 哈夫曼解压 最简单的方式实现哈夫曼树
阅读目录
-
-
- 基本概述
- 构建赫夫曼树 思路
- Python实现构建赫夫曼树
-
- 补充知识点:列表中如何按照元素的对象、类进行排序?
- 实现 创建赫夫曼树
- 赫夫曼编码
- 数据压缩:创建赫夫曼树
-
- 补充知识点:如何获取字符串的字节数?
- 补充知识点:如何统计出字符串中每个字符的次数?
- 补充知识点:如何给字典排序
- Python 实现数据压缩(创建赫夫曼树)
- 赫夫曼编码 和 赫夫曼编码后数据
-
- 补充知识点:如何遍历出二叉树的所有路径
- 实现赫夫曼编码
- 数据压缩:赫夫曼编码字节数组
- 封装代码
- 数据解压
-
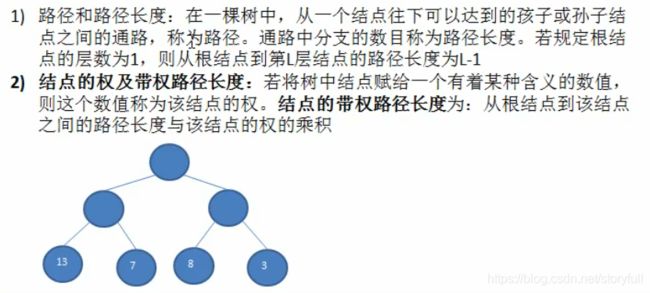
基本概述
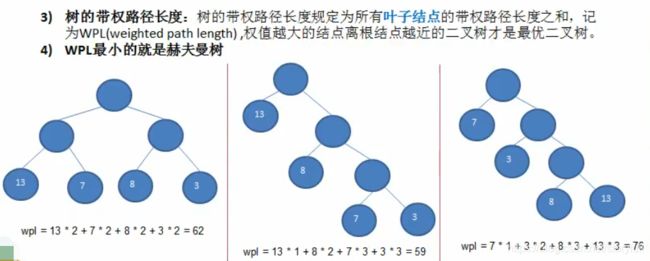
上图中,中间的二叉树,wpl最小,而且权值为13的结点,满足“权值越大离根结点越近” 那么它就是赫夫曼树!
构建赫夫曼树 思路
-
构建赫夫曼树的步骤
以数列:[13,7,8,3,29,6,1 ] 为例

注释:
(1)每一个结点可以看成一个二叉树,二叉树的分类中有说到
(2)取出排序后,前两个数;就是取出根结点权值最小的两颗二叉树 -
图解
(1)原数组 [13,7,8,3,29,6,1 ],第一次升序后:[1,3,6,7,8,13,29],取出前两个数(看下图的最底层),权值的和为新的根结点 4
(2)重新将数组连同刚刚产生的根结点4进行升序,数组为[4,6,7,8,13,29],此时选出的前两个数是4和6(看下图中的倒数第二层),让它们权值的和为新的根结点 10,将10放入剩下的未处理数组中:[10,7,8,13,29]
(3)再次升序时,会发现 10 应该排在 7和8的后面,所以升序后的数组为:[7,8,10,13,29],取出的前两个数是7和8,此时它们 应该和 根结点10 位于同一层,即倒数第三层,而且应该在10的前面(看下图的倒数第三层),因为它们是两个数 独立形成一个新的二叉树 那么在同一层的 [10,13,29] 前两个应该再生成一个新的根结点即是 23 (看下图倒数第四层)
(4)让7和8相加,形成新的根结点15 ,将15放入剩下的未处理数组中:[15,23,29],以此类推,具体看下图,下图是从底层向上操作的↓↓↓

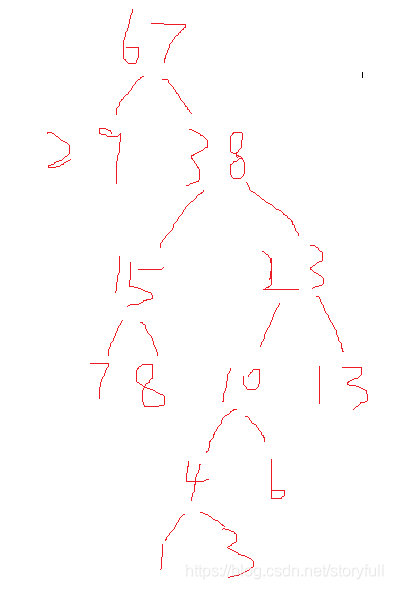
Python实现构建赫夫曼树
- 先解决:每次从列表中选出最小的2个数
(1)第一种思路:遍历数组,进行比较;思路很好,但是没调用内置排序方法效率高
array = [4, 20, 3, 4, 5, 6, 7]
num1 = num2 = float('inf')
for x in range(0, len(array)):
if num1 > array[x]:
num2 = num1
num1 = array[x]
elif num2 > array[x]:
num2 = array[x]
print(num1, num2)
补充知识点:列表中如何按照元素的对象、类进行排序?
- Java中通过实现 Comparable接口,可以给对象排序,Python中也可以在列表中按照元素的对象、类进行排序!
- 两种方法: operator模块中实现列表中的对象排序 和 如何用内置的sort()函数实现对象的排序
import operator # 导入operator 包,pip install operator
lis = [] # 待排序列表
class Infor: # 自定义的元素
def __init__(self, stu_id, name, age):
self.stu_id = stu_id
self.name = name
self.age = age
# 将对象加入列表中
lis.append(Infor(1, 'cbc', '11'))
lis.append(Infor(15, 'acd', '13'))
lis.append(Infor(6, 'bcd', '16'))
lis.append(Infor(6, 'acd', '18'))
lis.append(Infor(8, 'acd', '18'))
'''operater模块:适用于数据量大'''
# ----排序操作
# 参数为排序依据的属性,可以有多个,这里优先id,使用时按需求改换参数即可
temp = operator.attrgetter('stu_id', 'name')
lis.sort(key=temp) # 使用时改变列表名即可
# ----排序操作
# 此时lis已经变成排好序的状态了,排序按照stu_id优先,其次是name,遍历输出查看结果
for obj in lis:
print(obj.stu_id, obj.name, obj.age)
'''内置的sort()'''
lis.sort(cmp=None, key=lambda x:x.stu_id, reverse=False)
# lis.sort(cmp=None, key=lambda x:(x.stu_id,x.name,...), reverse=False) # 多个指标,前主后次
for obj in lis:
print(obj.stu_id, obj.name, obj.age)
注意:这两种方式都不能对空值进行操作,如果有空值会报错:TypeError: ‘<’ not supported between instances of ‘NoneType’ and ‘int’
解决办法是:将空值换成“0”,这点相对于java实现 Comparable接口方式,有点不方便
实现 创建赫夫曼树
import operator
class TreeNode(object):
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class HuffmanTree(object):
def create_huffman_tree(self, array):
'''
创建赫夫曼树的方法
:param array: 需要创建成赫夫曼树的数组
:return: 创建好后的赫夫曼树的root结点
'''
# 为了操作方便,先遍历array数组,将array的每个元素构成一个TreeNode
# 将TreeNode 对象放到 一个新的列表中
nodes = []
for item in array:
nodes.append(TreeNode(item))
# 对象排序
while len(nodes) > 1: # 到最后只有个新的根结点就停止
temp = operator.attrgetter("val")
nodes.sort(key=temp)
# 取出根结点权值最小的两颗二叉树(结点)
# left_node = nodes[0]
# right_node = nodes[1]
# 可以直接用pop第一个元素,下面的remove就不用写了
left_node = nodes.pop(0)
right_node = nodes.pop(0)
# 构建一棵新的二叉树
parent_node = TreeNode(left_node.val + right_node.val)
parent_node.left = left_node # 将父结点和左结点链接起来
parent_node.right = right_node
# 从nodes删除处理过的二叉树
# nodes.remove(left_node)
# nodes.remove(right_node)
# 将parent_node加入nodes
nodes.append(parent_node)
return nodes[0] # 返回根结点即可
def pre_order(self, node): # node 为根结点,前序遍历
if node is None:
return
print(node.val, end=" ")
self.pre_order(node.left)
self.pre_order(node.right)
if __name__ == '__main__':
li = [13, 7, 8, 3, 29, 6, 1]
h = HuffmanTree()
huff_root = h.create_huffman_tree(li)
h.pre_order(huff_root)
'''输出结果:
67 29 38 15 7 8 23 10 4 1 3 6 13
'''
赫夫曼编码
数据压缩:创建赫夫曼树
Python 实现
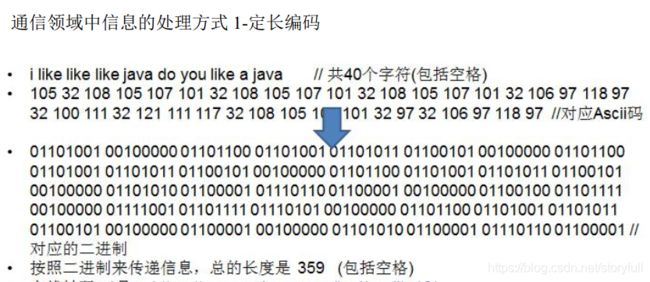
补充知识点:如何获取字符串的字节数?
(1)java中可以先用 getBytes 然后.length 获取字符串的字节数,Python可以通过 len()函数获取字符串长度或字节数
(2)len 函数的基本语法格式为:len(string) ,它的结果是获取字符串的长度
(3)在 Python 中,不同的字符所占的字节数不同,数字、英文字母、小数点、下划线以及空格,各占一个字节,而一个汉字可能占 2~4 个字节,具体占多少个,取决于采用的编码方式。例如,汉字在 GBK/GB2312 编码中占用 2 个字节,而在 UTF-8 编码中一般占用 3 个字节。
以 UTF-8 编码为例,字符串“人生苦短,我用Python”所占用的字节数如下图所示。

可以通过使用 encode() 方法,将字符串进行编码后再获取它的字节数。例如,采用 UTF-8 编码方式,计算“人生苦短,我用Python”的字节数:
# utf-8
str1 = "人生苦短,我用Python"
print(len(str1.encode())) # 27
# 汉字加中文标点符号共 7 个,占 21 个字节,而英文字母和英文的标点符号占 6 个字节,
# 一共占用 27 个字节
# gbk
str1 = "人生苦短,我用Python"
print(len(str1.encode('gbk'))) # 20
补充知识点:如何统计出字符串中每个字符的次数?
- 方法一:直接使用字典
'''法一'''
s = 'helloworld'
d = dict()
for x in s:
if x not in d:
d[x] = 1
else:
d[x] = d[x] + 1
print(d) # {'h': 1, 'e': 1, 'l': 3, 'o': 2, 'w': 1, 'r': 1, 'd': 1}
'''法二'''
s = 'helloworld'
d2 = dict()
for x in s:
d2[x] = d2.get(x, 0) + 1
print(d2) # {'h': 1, 'e': 1, 'l': 3, 'o': 2, 'w': 1, 'r': 1, 'd': 1}
'''法三:字符串count结合使用'''
s = 'helloworld'
d3 = dict()
for x in s:
d3[x] = s.count(x)
print(d3) # {'h': 1, 'e': 1, 'l': 3, 'o': 2, 'w': 1, 'r': 1, 'd': 1}
# 至于先用set()集合去重,然后遍历原字符串用count统计出现次数的方法,类似就不加赘述了
- 方式二:制表
def count_char(str):
str = str.lower() # 化成小写
ans = []
for i in range(26): # 列表赋初值 26 个 0
ans.append(0)
for i in str:
if (ord(i) >= ord('a') and ord(i) <= ord('z')):
ans[ord(i) - ord('a')] = ans[ord(i) - ord('a')] + 1 # 统计个数
return ans
if __name__ == "__main__":
str = input()
print(count_char(str))
#-------
def count_char(st): # 定义数个数的函数
keys = [chr(i + 97) for i in range(26)] # 生成26个字母的key列表
di = dict().fromkeys(keys, 0) # 赋给每个key初始值0
new = [] # 建立一个新列表用于存放有序的key
st = st.lower() # 将所有输入的字符改为小写
for s in st: # 遍历字符串
di[s] = st.count(s) # 输出每个字符的个数,存放到字典里
for k in keys: # 遍历keys,将其在di中的值添加到新列表,获得有序的26个字母的个数
new.append(di[k])
return new # 返回存有26个字母个数的列表
if __name__ == "__main__":
st = input() # 输入字符串
str1 = "" # 定义一个空字符串
for s in st: # 遍历输入的字符串
if s.isalpha() != 0: # 只有字母才添加到新字符串,标点忽略不计
str1 += s
print(count_char(str1)) # 输出列表
- 方法三:Counter(计数器):用于追踪值的出现次数;Counter类继承dict类,所以它能使用dict类里面的方法
特别注意: 它的统计输出是无序的
'''直接导入类用法'''
from collections import Counter
str_exp = ' aaffbbcccdddee '
c = Counter() # 先新建实例
for ele in str_exp:
c[ele] = c[ele] + 1
print(c, type(c)) # Counter({'c': 3, 'd': 3, ' ': 2, 'a': 2, 'f': 2, 'b': 2, 'e': 2})
# 注意c的类型不是字典:'''导入collections模块'''
import collections
obj = collections.Counter('aabbccc')
print(obj)
# 输出:Counter({'c': 3, 'a': 2, 'b': 2}) 它的类型不是字典是
'''elements()方法'''
import collections
obj = collections.Counter('aabbccc')
print(sorted(obj.elements()))
#输出:['a', 'a', 'b', 'b', 'c', 'c', 'c']
for k in obj.elements(): #遍历打印obj所有元素
print(k)
'''most_common(指定一个参数n,列出前n个元素,不指定参数,则列出所有)'''
import collections
obj = collections.Counter('aabbbcccc')
print(obj.most_common(2))
#输出:[('c', 4), ('b', 3)]
'''items(从dict类中继承的方法)'''
import collections
obj = collections.Counter('aabbbcccc')
print(obj.items())
for k,v in obj.items():
print(k,v)
# 输出:dict_items([('b', 3), ('c', 4), ('a', 2)])
# b 3
# c 4
# a 2
'''update(增加元素)'''
import collections
obj = collections.Counter(['11','22'])
obj.update(['22','55'])
print(obj)
#输出:Counter({'22': 2, '11': 1, '55': 1})
'''subtract(原来的元素减去新传入的元素)'''
import collections
obj = collections.Counter(['11','22','33'])
obj.subtract(['22','55'])
print(obj)
#输出:Counter({'11': 1, '33': 1, '22': 0, '55': -1})
补充知识点:如何给字典排序
- 说明:给字典排序 是为了让最后创建的结果更贴近所参考的教程,总体wpl是一样的,所以排不排序都无所谓;因为java在使用map[key,value] 在统计字符串出现的次数时,会自动按照 key 的大小升序排列!
- 字典排序的方法,字典用法的总结:字典排序
Python 实现数据压缩(创建赫夫曼树)
import operator
from collections import Counter
from operator import itemgetter
class TreeNode(object):
def __init__(self, val, weight):
self.val = val # 存放数据(字符)本身,如"a" 或者"97"
self.weight = weight # 存放出现的次数
self.left = None
self.right = None
class HuffmanCode(object):
def get_nodes(self, bytes_array):
nodes = []
# 存储每个byte出现的次数
# 统计一个字符串中每个元素出现的次数有很多种,这里为了操作方便,用Counter
'''法一
c = Counter() # 创建一个统计对象
for item in bytes_array:
c[item] = c[item] + 1
# 此时 c 会用字典的形式保存:key:每个元素;value:出现的次数
'''
# 法二 使用字典
dic = {
}
for i in bytes_array:
if i not in dic:
dic[i] = 1
else:
dic[i] += 1
'''如果不排序
for key, value in dic.items():
nodes.append(TreeNode(key, value))
'''
'''第一种排序 键值对 方式:
dic_list = sorted(dic.items(), key=lambda x: x[0])
print(dic_list)
for index, value in enumerate(dic_list): # 拿到 每一组键值对
nodes.append(TreeNode(value[0], value[1])) # 创建结点对象
'''
# 第二种排序 键值对 方式:
dic_list = sorted(dic.items(), key=itemgetter(0), reverse=False)
for item in dic_list:
nodes.append(TreeNode(item[0], item[1]))
return nodes
def create_huffman_tree(self, nodes):
while len(nodes) > 1:
# 法一:nodes.sort(key=lambda x: x.weight)
# 法二
nodes.sort(key=operator.attrgetter("weight"))
# 取出根结点权值最小的两颗二叉树(结点)
left_node = nodes.pop(0)
right_node = nodes.pop(0)
# 构建一棵新的二叉树,它的根结点(不是叶子结点)没有val,用0补充;含有weight
parent_node = TreeNode(0, left_node.weight + right_node.weight)
parent_node.left = left_node # 将父结点和左结点链接起来
parent_node.right = right_node
# 将parent_node加入nodes
nodes.append(parent_node)
return nodes[0] # 返回根结点即可
def pre_order(self, node): # 前序遍历 传入node为根结点
if node is None:
return
print(node.val, node.weight, end=" || ")
self.pre_order(node.left)
self.pre_order(node.right)
if __name__ == '__main__':
content = "i like like like java do you like a java"
# content_bytes = list(content.encode('utf-8'))
content_bytes = content.encode('utf-8')
print(len(content_bytes))
h = HuffmanCode()
# 获取到结点列表
obj_list = h.get_nodes(content_bytes)
# 获取到赫夫曼树的根结点
huffman_root = h.create_huffman_tree(obj_list)
# 前序遍历
h.pre_order(huffman_root)
'''
40
[(32, 9), (97, 5), (100, 1), (101, 4), (105, 5), (106, 2), (107, 4), (108, 4), (111, 2), (117, 1), (118, 2), (121, 1)] # 只是给字典排了下序
0 40 || 0 17 || 0 8 || 108 4 || 0 4 || 111 2 || 118 2 || 32 9 || 0 23 || 0 10 || 97 5 || 105 5 || 0 13 || 0 5 || 0 2 || 100 1 || 117 1 || 0 3 || 121 1 || 106 2 || 0 8 || 101 4 || 107 4 ||
# 赫夫曼树在处理weight一样时,是按照排序规则来合并结点,所以形态会不一样,但是最后根结点是一样的,
所以 看val为空的结点,间隔不管形态如何,间隔一定会一样的
'''
赫夫曼编码 和 赫夫曼编码后数据
- 到这一步,我们要做的是编码,因为所有的val有值得结点,必然是位于赫夫曼树的叶子节点,按照上面的规定,从根结点出发,遍历每一条到叶子结点的路径,走过的路径向左则为0,向右则为1,因为之前学过遍历二叉树路径的方法,所以可以这样很巧妙的完成!
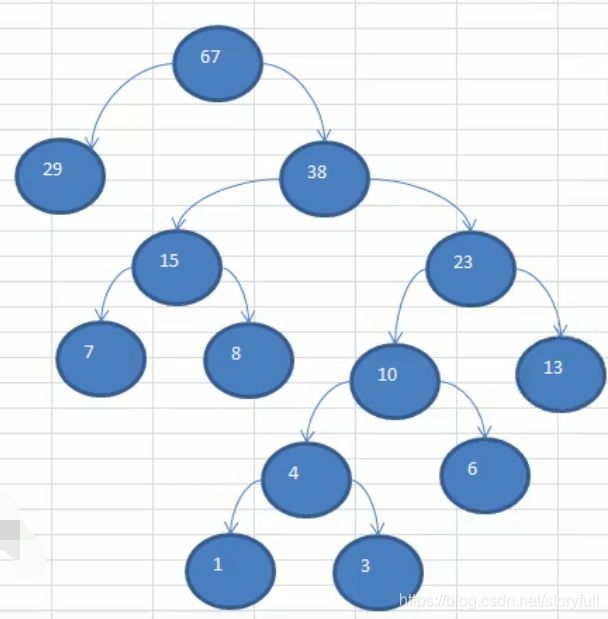
补充知识点:如何遍历出二叉树的所有路径
- 如下图有一颗10个结点的二叉树:

- 该怎么求它的所有路径?我们可以这样做
(1)在什么情况下输出结点?假设只有一个根结点root,它没有左右子结点,此时就输出结点的值,所以如上图的二叉树,我们使用递归,找到每一个没有左右子结点的结点,如上图是:[7,8,9,5,6],所以我们的递归退出条件找到了,即是:存在当前结点并且它没有左右子结点了,那么就退出
(2)为了串联起走过的路径,我们需要新增一个全局变量path,每次将走过的结点以字符串的形式串联起来,新增一个结果列表,输出最后结果!
class TreeNote(object): # 创建树的结点
def __init__(self, val=-1):
self.val = val
self.left = None
self.right = None
class BinaryTree(object): # 创建二叉树
def __init__(self):
self.root = None # 根结点
def add(self, val): # 二叉树添加结点
node = TreeNote(val)
if self.root is None:
self.root = node
return
queue = [self.root]
while queue:
temp_node = queue.pop(0)
if temp_node.left is None:
temp_node.left = node
return
else:
queue.append(temp_node.left)
if temp_node.right is None:
temp_node.right = node
return
else:
queue.append(temp_node.right)
def bre_order(self, node): # 二叉树广度遍历
if node is None:
return
queue = [node]
while queue:
temp_node = queue.pop(0)
print(temp_node.val, end=" ")
if temp_node.left is not None:
queue.append(temp_node.left)
if temp_node.right is not None:
queue.append(temp_node.right)
def find_rode(self, node, path, res): # node:传入root;path:路径;res:结果
if node is None:
return []
if node.left is None and node.right is None: # 当前结点没有左右子结点
res.append(path + str(node.val))
return res
if node.left: # 向左递归
self.find_rode(node.left, path + str(node.val), res)
if node.right: # 向右递归
self.find_rode(node.right, path + str(node.val), res)
if __name__ == '__main__':
t = BinaryTree()
for i in range(10):
t.add(i)
print("\n广度遍历为:")
t.bre_order(t.root)
print()
out_put = []
t.find_rode(t.root, "", out_put)
print("二叉树所有路径为:")
print(out_put)
'''
广度遍历为:
0 1 2 3 4 5 6 7 8 9
二叉树所有路径为:
['0137', '0138', '0149', '025', '026']
'''
实现赫夫曼编码
- 知道了怎么求二叉树的所有路径,那么就可以轻松求出赫夫曼树所有路径,按照新规定:走过的路径我们只需要拿到叶子结点的 val 即可,其他结点不需要拿val,路径则按照左边以“0”替换,右边以“1”替换,即可!
import operator
from operator import itemgetter
class TreeNode(object):
def __init__(self, val, weight):
self.val = val # 存放数据(字符)本身,如"a" 或者"97"
self.weight = weight # 存放出现的次数
self.left = None
self.right = None
class HuffmanCode(object):
# 返回赫夫曼树的结点列表
def get_nodes(self, bytes_array):
nodes = []
dic = {
}
for i in bytes_array:
if i not in dic:
dic[i] = 1
else:
dic[i] += 1
# 第二种排序 键值对 方式:
dic_list = sorted(dic.items(), key=itemgetter(0), reverse=False)
for item in dic_list:
nodes.append(TreeNode(item[0], item[1]))
return nodes
# 构建赫夫曼树,返回赫夫曼树的根结点
def create_huffman_tree(self, nodes):
while len(nodes) > 1:
nodes.sort(key=operator.attrgetter("weight"))
# 取出根结点权值最小的两颗二叉树(结点)
left_node = nodes.pop(0)
right_node = nodes.pop(0)
# 构建一棵新的二叉树,它的根结点,没有val,只有weight
parent_node = TreeNode(0, left_node.weight + right_node.weight)
parent_node.left = left_node # 将父结点和左结点链接起来
parent_node.right = right_node
# 将parent_node加入nodes
nodes.append(parent_node)
return nodes[0] # 返回根结点即可
# 为了更好比对图,我们可以使用 广度遍历测试
def bre_order(self, node):
if node is None:
return
queue = [node]
while queue:
temp_node = queue.pop(0)
print(temp_node.val, temp_node.weight, end=" || ")
if temp_node.left:
queue.append(temp_node.left)
if temp_node.right:
queue.append(temp_node.right)
# 获取赫夫曼编码表
def get_codes(self, node, path, temp):
if node is None:
return
if node.left is None and node.right is None:
temp.append(path + "|" + str(node.val)) # 中间新增一个分割符号,最后更好拿到编码和val
return temp
if node.left:
self.get_codes(node.left, path + "0", temp) # 左边让路径不断加上“0”
if node.right:
self.get_codes(node.right, path + "1", temp) # 左边让路径不断加上“1”
if __name__ == '__main__':
content = "i like like like java do you like a java"
content_bytes = content.encode('utf-8')
print(len(content_bytes))
h = HuffmanCode()
# 获取到结点列表
obj_list = h.get_nodes(content_bytes)
# 获取到赫夫曼树的根结点
huffman_root = h.create_huffman_tree(obj_list)
h.bre_order(huffman_root)
print()
# 赫夫曼编码
out_put = []
h.get_codes(huffman_root, "", out_put)
for item in out_put:
print(chr(int(item.split("|")[1])), item.split("|")[0], end=";")
print()
'''输出结果为
40
0 40 || 0 17 || 0 23 || 0 8 || 32 9 || 0 10 || 0 13 || 108 4 || 0 4 || 97 5 || 105 5 || 0 5 || 0 8 || 111 2 || 118 2 || 0 2 || 0 3 || 101 4 || 107 4 || 100 1 || 117 1 || 121 1 || 106 2 ||
val对应的编码为:
l 000;
o 0010;
v 0011;
01;
a 100;
i 101;
d 11000;
u 11001;
y 11010;
j 11011;
e 1110;
k 1111;
'''
- 验证一下是否正确:因为得到的赫夫曼树形态有可能不一样,得到的编码也不一样,但是按照上面写的,最后将上面每个val对应的新编码值,去组合一下输入的字符串,得到的字符长度要为:133
# 验证:手动输入(下一节实现自动生成如下编码,并且按照每八位压缩)
final_str = "1010100010100111110010001010011111001000101001111100111011100001110001110000010011101000101100101000101001111100110001110111000011100"
print(len(final_str)) # 133 恭喜我们做对了!
数据压缩:赫夫曼编码字节数组
- 按照上述步骤我们已经得到了每一个val的赫夫曼编码,并且存放在了数组中,接下来要做的就是自动将数组里的值生成上面的验证的:final_str 并且按8位 生成 赫夫曼编码字节数组
- 对于上面我们用 out_put = [ ] 列表来保存数据,我们可以改成,在生成赫夫曼编码时直接用字典来保存每条路径,即是:dict[node.val]=path 这样在处理自动将输入的字符串转成赫夫曼编码,可以充分利用字典的特性,所以下面整体代码为:
import operator
from operator import itemgetter
class TreeNode(object):
def __init__(self, val, weight):
self.val = val # 存放数据(字符)本身,如"a" 或者"97"
self.weight = weight # 存放出现的次数
self.left = None
self.right = None
class HuffmanCode(object):
# 返回赫夫曼树的结点列表
def get_nodes(self, bytes_array):
nodes = []
dic = {
}
for i in bytes_array:
if i not in dic:
dic[i] = 1
else:
dic[i] += 1
# 第二种排序 键值对 方式:
dic_list = sorted(dic.items(), key=itemgetter(0), reverse=False)
for item in dic_list:
nodes.append(TreeNode(item[0], item[1]))
return nodes
# 构建赫夫曼树,返回赫夫曼树的根结点
def create_huffman_tree(self, nodes):
while len(nodes) > 1:
nodes.sort(key=operator.attrgetter("weight"))
# 取出根结点权值最小的两颗二叉树(结点)
left_node = nodes.pop(0)
right_node = nodes.pop(0)
# 构建一棵新的二叉树,它的根结点,没有val,只有weight
parent_node = TreeNode(0, left_node.weight + right_node.weight)
parent_node.left = left_node # 将父结点和左结点链接起来
parent_node.right = right_node
# 将parent_node加入nodes
nodes.append(parent_node)
return nodes[0] # 返回根结点即可
# 为了更好比对图,我们可以使用 广度遍历测试
def bre_order(self, node):
if node is None:
return
queue = [node]
while queue:
temp_node = queue.pop(0)
print(temp_node.val, temp_node.weight, end=" || ")
if temp_node.left:
queue.append(temp_node.left)
if temp_node.right:
queue.append(temp_node.right)
# 获取赫夫曼编码(每一条路径)
def get_codes(self, node, path, temp):
if node is None:
return
if node.left is None and node.right is None:
temp[str(node.val)] = path # 改成字典来保存路径
return temp
if node.left:
self.get_codes(node.left, path + "0", temp) # 左边让路径不断加上“0”
if node.right:
self.get_codes(node.right, path + "1", temp) # 左边让路径不断加上“1”
def zip_codes(self, codes_array, srt_byte_content, str_join): # 充分利用字典特性
# 参数:传入赫夫曼编码数组,传入一个字节字符串,拼接字符串
for item in srt_byte_content: # 遍历每一个字符串字节
str_join += str(codes_array.get(str(item))) # 通过字节作为key,去找它的值,再拼接
return str_join
if __name__ == '__main__':
content = "i like like like java do you like a java"
content_bytes = content.encode('utf-8')
# print(len(content_bytes))
h = HuffmanCode()
# 获取到结点列表
obj_list = h.get_nodes(content_bytes)
# 获取到赫夫曼树的根结点
huffman_root = h.create_huffman_tree(obj_list)
# 广度遍历
# h.bre_order(huffman_root)
# 编码后
out_put = {
} # 改成字典
h.get_codes(huffman_root, "", out_put)
str_join = " "
final_str = h.zip_codes(out_put, content_bytes, str_join)
print(final_str)
''' 输出结果
1010100010111111110010001011111111001000101111111100111011100001110001110000010011101000
101100101000101111111100110001110111000011100
'''
- 接下来需要将自动获取到的字符串 转成 byte数组
(1)先要创建一个存下字符串的数组,有两种方式计算需要的数组长度,但是Python不需要规定长度也行,直接append添加每8个一组,最后多少都无所谓,emmmm!!!
第一种写法:
if len(str_join) % 8 == 0: # 自动获取的字符串长度先模上8
byte_array_len = len(str_join) / 8
else:
byte_array_len = len(str_join) // 8 + 1
byte_array = [0] * byte_array_len
print(len(byte_array)) # 17
第二种写法:
byte_array_len = (len(str_join) + 7) // 8
byte_array = [0] * byte_array_len
print(len(byte_array)) # 17
实现赫夫曼编码 转成 byte数组
'''上面代码一模一样就不拷贝了'''
def zip_codes(self, codes_array, srt_byte_content, str_join): # 参数:传入一个字节字符串,传入赫夫曼编码数组
for item in srt_byte_content:
str_join += str(codes_array.get(str(item)))
byte_array = []
final_byte_array = []
for i in range(1, len(str_join), 8): # 步长取8,从第二位开始,第一位是个空格
byte_array.append(str_join[i:i + 8])
for item in byte_array:
print(item) # 输出检查
if item[0] == "1":
final_byte_array.append(int(item, base=2) - 256) # 说明一
else:
final_byte_array.append(int(item, base=2))
return final_byte_array
if __name__ == '__main__':
content = "i like like like java do you like a java"
content_bytes = content.encode('utf-8')
# print(len(content_bytes))
h = HuffmanCode()
# 获取到结点列表
obj_list = h.get_nodes(content_bytes)
# 获取到赫夫曼树的根结点
huffman_root = h.create_huffman_tree(obj_list)
# 前序遍历
# h.pre_order(huffman_root)
# print()
# h.bre_order(huffman_root)
# print()
# 编码后
out_put = {
}
h.get_codes(huffman_root, "", out_put)
str_join = " "
# final_str = h.zip_codes(out_put, content_bytes, str_join)
final_byte = h.zip_codes(out_put, content_bytes, str_join)
print(final_byte)
print(len(final_byte)
'''输出结果
10101000
10111111
11001000
10111111
11001000
10111111
11001110
11100001
11000111
00000100
11101000
10110010
10001011
11111100
11000111
01110000
11100
[-88, -65, -56, -65, -56, -65, -50, -31, -57, 4, -24, -78, -117, -4, -57, 112, -228]
17
---
可以计算压缩率为:(40-17)/ 40 = 0.575
'''
- 说明一:默认切割出来的每八位,在计算机底层应该将它当做补码 才能进行存储,所以符号位为1的二进制码,表明它的原码是一个负数,那么怎么通过补码求出该数的十进制数?可以用快捷方法:算出补码无视符号位在二进制中的数 减去 256 即可!可以自行通过每个切割出来的字符串,当做补码然后求出它的原码,去掉符号位,求出二进制数,来验证!
封装代码
- 为了调用方便,我们将代码都封装到一个方法里,然后主函数调用该方法执行,主函数声明的全局变量,也都放入到一个类中,于是代码可以精简为:↓↓↓
import operator
from operator import itemgetter
class TreeNode(object):
def __init__(self, val, weight):
self.val = val # 存放数据(字符)本身,如"a" 或者"97"
self.weight = weight # 存放出现的次数
self.left = None
self.right = None
class HuffmanCode(object):
out_put_dic = {
} # 键值对:字符字节:赫夫曼编码
str_join = "" # 拼接字符串
# 返回赫夫曼树的结点列表
def get_nodes(self, bytes_array):
nodes = []
dic = {
}
for i in bytes_array:
if i not in dic:
dic[i] = 1
else:
dic[i] += 1
# 给键值对 排序(可以有可无)
dic_list = sorted(dic.items(), key=itemgetter(0), reverse=False)
for item in dic_list:
nodes.append(TreeNode(item[0], item[1]))
return nodes
# 构建赫夫曼树,返回赫夫曼树的根结点
def create_huffman_tree(self, nodes):
while len(nodes) > 1:
nodes.sort(key=operator.attrgetter("weight"))
# 取出根结点权值最小的两颗二叉树(结点)
left_node = nodes.pop(0)
right_node = nodes.pop(0)
# 构建一棵新的二叉树,它的根结点,没有val,只有weight
parent_node = TreeNode(0, left_node.weight + right_node.weight)
parent_node.left = left_node # 将父结点和左结点链接起来
parent_node.right = right_node
# 将parent_node加入nodes
nodes.append(parent_node)
return nodes[0] # 返回根结点即可
# 获取赫夫曼编码表
def get_codes(self, node, path, temp):
if node is None:
return
if node.left is None and node.right is None:
temp[str(node.val)] = path
return temp
if node.left:
self.get_codes(node.left, path + "0", temp)
if node.right:
self.get_codes(node.right, path + "1", temp)
return temp
def zip_codes(self, codes_array, srt_content_byte, str_join): # 参数:传入一个字节字符串,传入赫夫曼编码数组
for item in srt_content_byte:
str_join += str(codes_array.get(str(item)))
byte_array = []
final_byte_array = []
for i in range(0, len(str_join), 8): # 步长取8,从第二位开始,第一位是个空格
byte_array.append(str_join[i:i + 8])
for item in byte_array:
if item[0] == "1":
final_byte_array.append(int(item, base=2) - 256)
else:
final_byte_array.append(int(item, base=2))
return final_byte_array
def huffman_zip(self, bytes_array):
'''
封装
:param bytes_array: 传入一个原始字节数组
:return: 返回一个压缩字节数组
'''
nodes = self.get_nodes(bytes_array)
huffman_tree_root = self.create_huffman_tree(nodes)
codes_array = self.get_codes(huffman_tree_root, "", HuffmanCode.out_put_dic)
get_zip_byte = self.zip_codes(codes_array, bytes_array, HuffmanCode.str_join)
return get_zip_byte
if __name__ == '__main__':
content = "i like like like java do you like a java"
content_bytes = content.encode('utf-8')
h = HuffmanCode()
final = h.huffman_zip(content_bytes)
print(final)
'''输出结果
[-88, -65, -56, -65, -56, -65, -50, -31, -57, 4, -24, -78, -117, -4, -57, 112, -228]
'''
数据解压
- 第一步是还原回原来的赫夫曼编码字符串:即是通过最后的压缩字节数组,得到:“1010100010111111110010001011111111001000101111111100111011100001110001110000010011101000101100101000101111111100110001110111000011100” 我们可以遍历数组,如果是负数先加回265,如果是正数就不要加,但是这时候要注意两个重要问题:
(1)如果压缩字节数组还没遍历到最后一个数,遇到正数,在正数转成二进制码时,需要补齐八位,即前面要补上0凑足八位二进制;
(2)最后一位,如果是负数直接拼接起二进制码,如果是正数,不要补齐八位;因为前面我们在切割字符串时,是按照8位来切割的,最后剩下的,是直接转二进制的
'''前面代码一样,就省略下了'''
def be_back_str(self, huffman_array): # 调用后,返回拼接哈夫曼编码
# for ele in huffman_array: # 因为最后一个是负数,所以直接拼接上了,但是也可能是正数
# if ele < 0:
# HuffmanCode.str_join += str(bin(ele + 256))[2:]
# else:
# add_zero = 8 - len(bin(ele)[2:])
# HuffmanCode.str_join += ("0" * add_zero + bin(ele)[2:])
# print(HuffmanCode.str_join)
for i in range(len(huffman_array) - 1): # 遍历到数组前一个
if huffman_array[i] < 0:
HuffmanCode.str_join += str(bin(huffman_array[i] + 256))[2:]
else:
add_zero = 8 - len(bin(huffman_array[i])[2:])
HuffmanCode.str_join += ("0" * add_zero + bin(huffman_array[i])[2:])
if huffman_array[-1] < 0: # 考虑最后一个数的两种情况
HuffmanCode.str_join += bin(huffman_array[-1] + 256)[2:]
else:
HuffmanCode.str_join += bin(huffman_array[-1])[2:]
print(HuffmanCode.str_join) # 打印测试下
if __name__ == '__main__':
content = "i like like like java do you like a java"
content_bytes = content.encode('utf-8')
h = HuffmanCode()
final = h.huffman_zip(content_bytes)
print(final)
h.be_back_str(final)
'''输出结果:
101010001011111111001000101111111100100010111111110011101110000111000111
0000010011101000101100101000101111111100110001110111000011100
比较和前面的一致
'''
- 第二步,查找字符串,然后去原来的字典查值,得到字节数组,最后返回原来的字符串;这里要用到字符串的查找!
完整代码
import operator
from operator import itemgetter
class TreeNode(object):
def __init__(self, val, weight):
self.val = val # 存放数据(字符)本身,如"a" 或者"97"
self.weight = weight # 存放出现的次数
self.left = None
self.right = None
class HuffmanCode(object):
out_put_dic = {
} # 键值对:字符字节:赫夫曼编码
str_join = "" # 拼接字符串
final_bytes = []
# 返回赫夫曼树的结点列表
def get_nodes(self, bytes_array):
nodes = []
dic = {
}
for i in bytes_array:
if i not in dic:
dic[i] = 1
else:
dic[i] += 1
# 给键值对 排序(可以有可无)
dic_list = sorted(dic.items(), key=itemgetter(0), reverse=False)
for item in dic_list:
nodes.append(TreeNode(item[0], item[1]))
return nodes
# 构建赫夫曼树,返回赫夫曼树的根结点
def create_huffman_tree(self, nodes):
while len(nodes) > 1:
nodes.sort(key=operator.attrgetter("weight"))
# 取出根结点权值最小的两颗二叉树(结点)
left_node = nodes.pop(0)
right_node = nodes.pop(0)
# 构建一棵新的二叉树,它的根结点,没有val,只有weight
parent_node = TreeNode(0, left_node.weight + right_node.weight)
parent_node.left = left_node # 将父结点和左结点链接起来
parent_node.right = right_node
# 将parent_node加入nodes
nodes.append(parent_node)
return nodes[0] # 返回根结点即可
# 获取赫夫曼编码表
def get_codes(self, node, path, temp):
if node is None:
return
if node.left is None and node.right is None:
temp[str(node.val)] = path
return temp
if node.left:
self.get_codes(node.left, path + "0", temp)
if node.right:
self.get_codes(node.right, path + "1", temp)
return temp
def zip_codes(self, codes_array, srt_content_byte, str_join): # 参数:传入一个字节字符串,传入赫夫曼编码数组
for item in srt_content_byte:
str_join += str(codes_array.get(str(item)))
byte_array = []
final_byte_array = []
for i in range(0, len(str_join), 8): # 步长取8,从第二位开始,第一位是个空格
byte_array.append(str_join[i:i + 8])
for item in byte_array:
if item[0] == "1":
final_byte_array.append(int(item, base=2) - 256)
else:
final_byte_array.append(int(item, base=2))
return final_byte_array
def huffman_zip(self, bytes_array):
'''
封装
:param bytes_array: 传入一个原始字节数组
:return: 返回一个压缩字节数组
'''
nodes = self.get_nodes(bytes_array)
huffman_tree_root = self.create_huffman_tree(nodes)
codes_array = self.get_codes(huffman_tree_root, "", HuffmanCode.out_put_dic)
get_zip_byte = self.zip_codes(codes_array, content_bytes, HuffmanCode.str_join)
return codes_array, get_zip_byte
def be_back_str(self, huffman_array, codes_dict):
'''
:param huffman_array: 最后返回的哈夫曼编码字节数组
:param codes_dict: 最开始存放字节对应的编码,键值对为>>>字节:哈夫曼编码
:return: 返回原来的字符串
'''
for i in range(len(huffman_array) - 1):
if huffman_array[i] < 0:
HuffmanCode.str_join += str(bin(huffman_array[i] + 256))[2:]
else:
add_zero = 8 - len(bin(huffman_array[i])[2:])
HuffmanCode.str_join += ("0" * add_zero + bin(huffman_array[i])[2:])
if huffman_array[-1] < 0:
HuffmanCode.str_join += bin(huffman_array[-1] + 256)[2:]
else:
HuffmanCode.str_join += bin(huffman_array[-1])[2:]
# 键值逆置 方便查找,开始键位布局不好,只能这里修改了,哭了
codes_dict = dict(zip(codes_dict.values(), codes_dict.keys()))
# 切割赫夫曼编码字符串,比对字典,添加到查找的内容到列表
i = 0
while i < len(HuffmanCode.str_join):
count = 1
flag = True
b = None
while flag:
key = HuffmanCode.str_join[i:i + count] # i不动,让count移动,指定到匹配一个字符串
b = codes_dict.get(key) # get()方法,如果没找到会返回一个None
if b is None:
count += 1
else:
flag = False
HuffmanCode.final_bytes.append(b)
i += count
temp = " "
for item in HuffmanCode.final_bytes:
temp += str(chr(int(item)))
return temp
if __name__ == '__main__':
content = "i like like like java do you like a java"
content_bytes = content.encode('utf-8')
h = HuffmanCode()
final = h.huffman_zip(content_bytes)
print(final[1])
last_back_str = h.be_back_str(final[1], final[0])
print(last_back_str)
'''
[-88, -65, -56, -65, -56, -65, -50, -31, -57, 4, -24, -78, -117, -4, -57, 112, -228]
i like like like java do you like a java
'''