【ACM专题训练】深度优先搜索/抽象的深度优先搜索/深搜的剪枝操作
中国象棋
中国象棋博大精深,其中马的规则最为复杂,也是最难操控的一颗棋子。
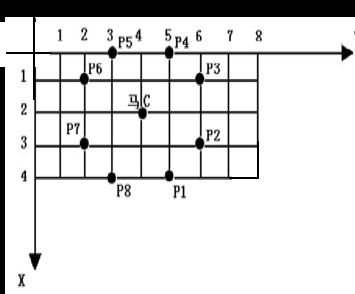
我们都知道象棋中马走"日",比如在 (2, 4)位置的一个马,跳一步能到达的位置有 (0, 3),(0,5),(1,2),(1,6),(3,2),(3,6),(4, 3),(4,5)。
蒜头君正在和花椰妹下棋,蒜头君正在进行战略布局,他需要把在 (x,y) 位置的马跳到 (x′,y′) 位置,以达到威慑的目的。
但是棋盘大小有限制,棋盘是一个 10×9 的网格,左上角坐标为(0,0),右下角坐标为(9,8),马不能走出棋盘,并且有些地方已经有了棋子,马也不能跳到有棋子的点。
蒜头君想知道,在不移动其他棋子的情况下,能否完成他的战略目标。
输入格式
输入一共 10 行,每行一个长度为 9 的字符串。
输入表示这个棋盘,我们用'.'表示空位置,用'#'表示该位置有棋子,用'S'表示初始的马的位置,用'T'表示马需要跳到的位置。
输入保证一定只存在一个'S'和一个'T'。
输出格式
如果在不移动其他棋子的情况下,马能从'S'跳到'T',那么输出一行"Yes",否则输出一行"No"。
样例输入复制
.#....#S#
..#.#.#..
..##.#..#
......##.
...T.....
...#.#...
...#.....
...###...
.........
.##......样例输出复制
Yes#include
#include
#include
using namespace std;
int vis[15][15];
char s[15][15];
int sx,sy,ex,ey;
int step[10][2] = {
{1,2},{1,-2},{2,1},{2,-1},{-1,2},{-1,-2},{-2,1},{-2,-1}};
bool flag;
void dfs(int tx,int ty){
int x,y;
if(tx == ex && ty == ey){
flag = true;
return ;
}
if(tx < 0 || ty < 0 || tx > 9 || ty > 8){
return;
}
if(s[tx][ty] == '#')
return ;
if(flag)
return ;
if(vis[tx][ty]){
return ;
}
vis[tx][ty] = 1;
for(int i = 0;i < 8;i++){
x = tx + step[i][0];
y = ty + step[i][1];
f(x,y);
}
}
int main(){
for(int i = 0;i < 10;i++){
gets(s[i]);
for(int j = 0;j < 9;j++){
if(s[i][j] == 'S'){
sx = i;
sy = j;
}
else if(s[i][j] == 'T'){
ex = i;
ey = j;
}
}
}
dfs(sx,sy);
if(flag){
cout << "Yes";
}
else{
cout << "No";
}
return 0;
} 2n皇后问题
给定一个 n∗n 的棋盘,棋盘中有一些位置不能放皇后。现在要向棋盘中放入 n 个黑皇后和 n 个白皇后,使任意的两个黑皇后都不在同一行、同一列或同一条斜线(包括正负斜线)上,任意的两个白皇后都不在同一行、同一列或同一条斜线(包括正负斜线)上。问总共有多少种放法?n 小于等于 8。
输入格式
输入的第一行为一个整数 n,表示棋盘的大小。
接下来 n 行,每行 n 个 0 或 1 的整数,如果一个整数为 1,表示对应的位置可以放皇后,如果一个整数为 0,表示对应的位置不可以放皇后。
输出格式
输出一个整数,表示总共有多少种放法。
样例输入1复制
4
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1样例输出1复制
2样例输入2复制
4
1 0 1 1
1 1 1 1
1 1 1 1
1 1 1 1
样例输出2复制
0#include
#include
#include
#include
using namespace std;
int map[10][10];
int a[100],b[100],c[100],d[100];
int a1[100],b1[100],c1[100],d1[100];
//a数组表示的是行;
//b数组表示的是列;
//c表示的是左下到右上的对角线;
//d表示的是左上到右下的对角线;
int total;
int n; //输入的数,即N*N的格子,全局变量,搜索中要用
void queen2(int i) //搜索与回溯主体
{
if(i>n)
{
total++;
return;
}
else
{
for(int j=1;j<=n;j++) //尝试第i行中皇后a[i][j]可能的位置
{
if(!map[i][j])
continue;
if((!b1[j])&&(!c1[i+j])&&(!d1[i-j+n])) //i+j,i-j相同的在同一对角线,为避免参数小于0加上n
{
a1[i]=j;//标记i排是第j个
b1[j]=1;//宣布占领纵列
c1[i+j]=1;
d1[i-j+n]=1;
map[i][j] = 0;
//宣布占领两条对角线
queen2(i+1);
map[i][j] = 1;
a1[i]=0; //撤值清除标记,这一步可以省,但考虑程序整体性加上更便于理解
b1[j]=0;
c1[i+j]=0;
d1[i-j+n]=0;
}
}
}
}
void queen(int i) //搜索与回溯主体
{
if(i>n)
{
queen2(1);
return;
}
else
{
for(int j=1;j<=n;j++) //尝试第i行中皇后a[i][j]可能的位置
{
if(!map[i][j])
continue;
if((!b[j])&&(!c[i+j])&&(!d[i-j+n])) //i+j,i-j相同的在同一对角线,为避免参数小于0加上n
{
a[i]=j;//标记i排是第j个
b[j]=1;//宣布占领纵列
c[i+j]=1;
d[i-j+n]=1;
map[i][j] = 0;
//宣布占领两条对角线
queen(i+1);
map[i][j] = 1;
a[i]=0; //撤值清除标记,这一步可以省,但考虑程序整体性加上更便于理解
b[j]=0;
c[i+j]=0;
d[i-j+n]=0;
}
}
}
}
int main()
{
cin>>n;
for(int i = 1;i <=n;i++){
for(int j = 1;j <=n;j++){
cin >> map[i][j];
}
}
queen(1); //第一个皇后
cout << total;
return 0;
}
数独
蒜头君今天突然开始还念童年了,想回忆回忆童年。他记得自己小时候,有一个很火的游戏叫做数独。便开始来了一局紧张而又刺激的高阶数独。蒜头君做完发现没有正解,不知道对不对? 不知道聪明的你能否给出一个标准答案?
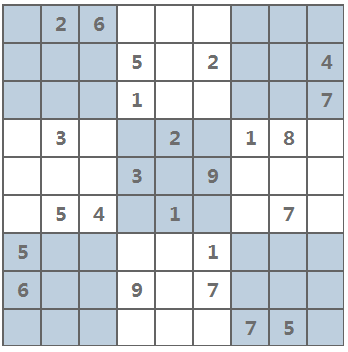
标准数独是由一个给与了提示数字的 9×9 网格组成,我们只需将其空格填上数字,使得每一行,每一列以及每一个 3×3 宫都没有重复的数字出现。
输入格式
一个9×9 的数独,数字之间用空格隔开。*表示需要填写的数字。
输出格式
输出一个9×9 的数独,把出入中的*替换成需要填写的数字即可。
本题答案不唯一,符合要求的答案均正确
样例输入复制
* 2 6 * * * * * *
* * * 5 * 2 * * 4
* * * 1 * * * * 7
* 3 * * 2 * 1 8 *
* * * 3 * 9 * * *
* 5 4 * 1 * * 7 *
5 * * * * 1 * * *
6 * * 9 * 7 * * *
* * * * * * 7 5 *样例输出复制
1 2 6 7 3 4 5 9 8
3 7 8 5 9 2 6 1 4
4 9 5 1 6 8 2 3 7
7 3 9 4 2 5 1 8 6
8 6 1 3 7 9 4 2 5
2 5 4 8 1 6 3 7 9
5 4 7 2 8 1 9 6 3
6 1 3 9 5 7 8 4 2
9 8 2 6 4 3 7 5 1#include
#include
#include
using namespace std;
int map[10][10];
bool visx[10][10],visy[10][10],visz[10][10];
bool flag;
char temp[10][10];
int cnt;
void print(){
for(int i = 0;i < 9;i++){
for(int j = 0;j < 9 ;j++){
if(j == 0){
cout << map[i][j];
}
else{
cout << " " << map[i][j];
}
}
cout << endl;
}
}
void dfs(int i,int j){
if(flag){
return ;
}
if(i == 9){
print();
flag = true;
return ;
}
if(map[i][j] == 0){
int id = i / 3 * 3 + j / 3;
for(int k = 1;k <= 9;k++){
if(!visx[i][k] && !visy[j][k] && !visz[id][k]){
map[i][j] = k;
visx[i][k] = visy[j][k] = visz[id][k] = true;
if(j < 8){
dfs(i,j+1);
}
else{
dfs(i+1,0);
}
map[i][j] = 0;
visx[i][k] = visy[j][k] = visz[id][k] = false;
}
}
}
else{
if(j < 8){
dfs(i,j+1);
}
else{
dfs(i+1,0);
}
}
}
int main(){
for(int i = 0;i < 9;i++){
for(int j = 0;j < 9;j++){
cin >> temp[i][j];
if(temp[i][j] == '0'){
map[i][j] == 0;
}
else{
map[i][j] = temp[i][j] - '0';
visx[i][map[i][j]] = true; //横
visy[j][map[i][j]] = true; //竖
visz[i/3*3+j/3][map[i][j]] = true; //宫
}
}
}
dfs(0,0);
return 0;
}