Python数据科学学习笔记之——机器学习
机器学习
1、什么是机器学习
机器学习经常被归类为人工智能的子领域,但我觉得这种归类方法存在误导嫌疑。虽然对机器学习的研究确实是源自人工智能领域,但是机器学习的方法却应用于数据科学领域,因此我认为机器学习看作是一种数学建模更合适。
机器学习的本质就是借助数学模型理解数据。当我们给模型装上可以适应观测数据的可调参数时,“学习” 就开始了;此时的程序被认为具有从数据中 “学习” 的能力。一旦模型可以拟合旧的观测数据,那么它们就可以预测并解释新的观测数据。
1.1、机器学习的分类
机器学习一般可分为两类:有监督的学习(supervised learning)和无监督的学习(unsupervised learning)。
- 有监督的学习:是指对数据的若干特征与若干标签(类型)之间的关联性进行建模的过程;只要模型被确定,就可以应用到新的未知数据上。这类学习过程可以进一步分为分类(classification)任务与回归(regression)任务。在分类任务中,标签是离散值;而在回归任务中,标签是连续值。
- 无监督学习:是指对不带任何标签的数据特征进行建模,通常被看成是一种 “让数据自己介绍自己” 的过程。这类模型包括聚类(clustering)任务和降维(dimensionality reduction)任务。聚类算法可以将数据分成不同的组别,而降维算法追求用更简洁的方式表现数据。
- 另外,还有一种半监督学习(semi-supervised learning)方法,介于有监督学习与无监督学习之间。半监督学习方法通常可以在数据标签不完整时使用。
1.2、机器学习应用的定性示例
1.2.1、分类:预测离散标签
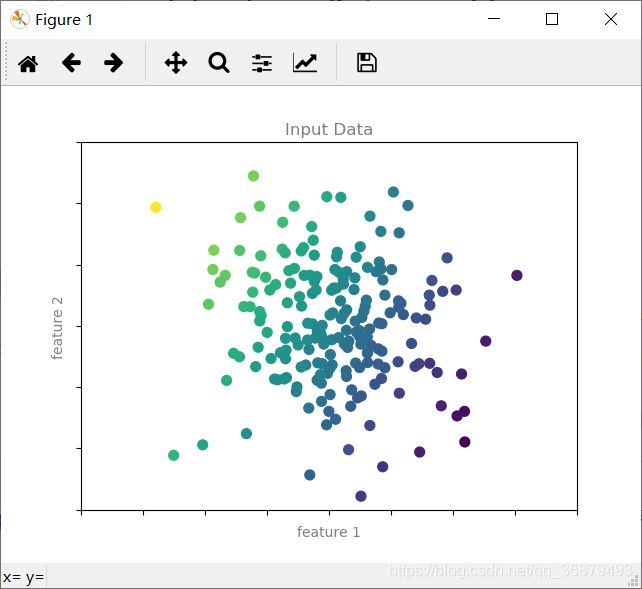
先来看一个简单的分类任务。假如我们有一些带标签的数据点,希望用这些信息为那些不带标签的数据点进行分类。假如这些数据点的分布如下:
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
# common plot formatting for below
def format_plot(ax, title):
ax.xaxis.set_major_formatter(plt.NullFormatter())
ax.yaxis.set_major_formatter(plt.NullFormatter())
ax.set_xlabel('feature 1', color='gray')
ax.set_ylabel('feature 2', color='gray')
ax.set_title(title, color='gray')
from sklearn.datasets.samples_generator import make_blobs
from sklearn.svm import SVC
# create 50 separable points
X, y = make_blobs(n_samples=50, centers=2,
random_state=0, cluster_std=0.60)
# fit the support vector classifier model
clf = SVC(kernel='linear')
clf.fit(X, y)
# create some new points to predict
X2, _ = make_blobs(n_samples=80, centers=2,
random_state=0, cluster_std=0.80)
X2 = X2[50:]
# predict the labels
y2 = clf.predict(X2)
# plot the data
fig, ax = plt.subplots(figsize=(8, 6))
point_style = dict(cmap='Paired', s=50)
ax.scatter(X[:, 0], X[:, 1], c=y, **point_style)
# format plot
format_plot(ax, 'Input Data')
ax.axis([-1, 4, -2, 7])
plt.show()
我们看到的是二维数据,也就是说每个数据点都有两个特征,在平面上用数据点的(x,y)位置表示。另外,我们的数据点还用一种颜色表示一个类型标签,一共有两种类型,分别用两种颜色表示。我们想根据这些特性和标签创建一个模型,帮助我们判断新的数据点是 “蓝色” 还是 “红色”。
虽然有许多可以解决分类任务的模型,但是这里还是先用最简单的一种。假设平面上有一条可以将两种类型分开的直线,直线的两侧分别是一种类型。那么,我们的模型其实就是 “一条可以分类的直线”,而模型参数其实就是直线位置与方向的数值。这些模型参数的最优解都可以通过学习数据获得(也就是机器学习的 “学习”),这个过程通常被称为训练模型。
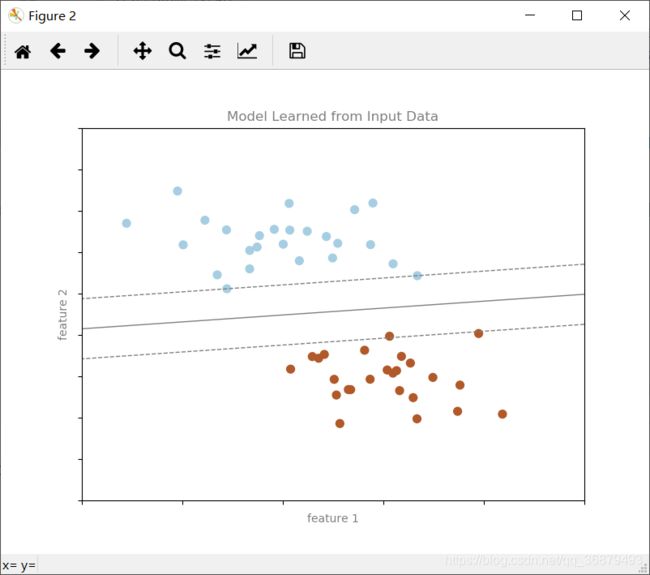
下图就是为这组数据分类而训练的模型:
# Get contours describing the model
xx = np.linspace(-1, 4, 10)
yy = np.linspace(-2, 7, 10)
xy1, xy2 = np.meshgrid(xx, yy)
Z = np.array([clf.decision_function([t])
for t in zip(xy1.flat, xy2.flat)]).reshape(xy1.shape)
# plot points and model
fig, ax = plt.subplots(figsize=(8, 6))
line_style = dict(levels = [-1.0, 0.0, 1.0],
linestyles = ['dashed', 'solid', 'dashed'],
colors = 'gray', linewidths=1)
ax.scatter(X[:, 0], X[:, 1], c=y, **point_style)
ax.contour(xy1, xy2, Z, **line_style)
# format plot
format_plot(ax, 'Model Learned from Input Data')
ax.axis([-1, 4, -2, 7])
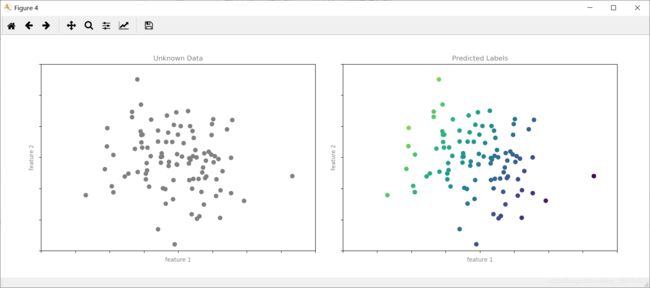
模型已经训练好了,可以对一个新的、不带标签的数据进行分类了。也就是说,我们可以拿一组新的数据,把这个模型的直线画在上面,然后根据这个模型为新数据分配标签。这个阶段通常被称为预测:
# plot the results
fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
ax[0].scatter(X2[:, 0], X2[:, 1], c='gray', **point_style)
ax[0].axis([-1, 4, -2, 7])
ax[1].scatter(X2[:, 0], X2[:, 1], c=y2, **point_style)
ax[1].contour(xy1, xy2, Z, **line_style)
ax[1].axis([-1, 4, -2, 7])
format_plot(ax[0], 'Unknown Data')
format_plot(ax[1], 'Predicted Labels')
这就是机器学习中最基本的分类思想,这个 “分类” 指的是数据具有离散的类型标签。机器学习方法的真正用途是要解决大型高维度数据集的分类问题。
以常见的分类任务——垃圾邮件自动识别为例。在这类任务中,我们通常会获得以下特征与标签。
- 特征1、特征2……特征 n → 垃圾邮件关键词与短语出现的频次归一化向量(“Viagra”、“Nigerian prince” 等)。
- 标签 → “垃圾邮件” 或 “普通邮件”。
在训练数据集中,这些标签可能是人们通过观察少量邮件样本得到的,而剩下的大量邮件都需要通过模型来判断标签。一个训练有素的分类算法只要具备足够好的特性(通常是成千上万个词或短语),就能非常高效地进行分类。
还有一些重要的分类算法:高斯朴素贝叶斯分类、支持向量机以及随机森林分类。
1.2.2、回归:预测连续标签
下面将介绍的回归任务与离散标签分类算法相反,其标签是连续值。
下图所示的数据集,所有样本的标签都在一个连续的区间内:
和前面的分类示例一样,我们有一个二维数据,每个数据点有两个特征。数据点的颜色表示每个点的连续标签。
虽然有很多可以处理这类数据的回归模型,但是我们还是用简单线性回归模型来预测数据。用简单线性回归模型做出假设,如果我们把标签看成是第三个维度,那么就可以将数据拟合成一个平面方程——这就是著名的在二维平面上线性拟合问题的高阶情形。
我们将数据可视化成下图:
from mpl_toolkits.mplot3d.art3d import Line3DCollection
points = np.hstack([X, y[:, None]]).reshape(-1, 1, 3)
segments = np.hstack([points, points])
segments[:, 0, 2] = -8
# plot points in 3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:, 0], X[:, 1], y, c=y, s=35,
cmap='viridis')
ax.add_collection3d(Line3DCollection(segments, colors='gray', alpha=0.2))
ax.scatter(X[:, 0], X[:, 1], -8 + np.zeros(X.shape[0]), c=y, s=10,
cmap='viridis')
# format plot
ax.patch.set_facecolor('white')
ax.view_init(elev=20, azim=-70)
ax.set_zlim3d(-8, 8)
ax.xaxis.set_major_formatter(plt.NullFormatter())
ax.yaxis.set_major_formatter(plt.NullFormatter())
ax.zaxis.set_major_formatter(plt.NullFormatter())
ax.set(xlabel='feature 1', ylabel='feature 2', zlabel='label')
# Hide axes (is there a better way?)
ax.w_xaxis.line.set_visible(False)
ax.w_yaxis.line.set_visible(False)
ax.w_zaxis.line.set_visible(False)
for tick in ax.w_xaxis.get_ticklines():
tick.set_visible(False)
for tick in ax.w_yaxis.get_ticklines():
tick.set_visible(False)
for tick in ax.w_zaxis.get_ticklines():
tick.set_visible(False)
fig.savefig('E:\practice\python\代码练习\Python数据科学\机器学习\\05.01-regression-2.png')
请注意,这里特征 1 与特征 2 平面与之前的二维图形是一样的,只不过用了颜色和三维坐标轴的位置表示标签。通过这个视角,就有理由相信:如果将三维数据拟合成一个平面,就可以对任何输入参数集进行预测。回到原来的二维投影图形上,拟合平面时获得的结果如图:
from matplotlib.collections import LineCollection
# plot data points
fig, ax = plt.subplots()
pts = ax.scatter(X[:, 0], X[:, 1], c=y, s=50,
cmap='viridis', zorder=2)
# compute and plot model color mesh
xx, yy = np.meshgrid(np.linspace(-4, 4),
np.linspace(-3, 3))
Xfit = np.vstack([xx.ravel(), yy.ravel()]).T
yfit = model.predict(Xfit)
zz = yfit.reshape(xx.shape)
ax.pcolorfast([-4, 4], [-3, 3], zz, alpha=0.5,
cmap='viridis', norm=pts.norm, zorder=1)
# format plot
format_plot(ax, 'Input Data with Linear Fit')
ax.axis([-4, 4, -3, 3])
fig.savefig('E:\practice\python\代码练习\Python数据科学\机器学习\\05.01-regression-3.png')
这个拟合平面为预测数据点的标签提供了依据。我们可以直观地找到结果:
# plot the model fit
fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
ax[0].scatter(X2[:, 0], X2[:, 1], c='gray', s=50)
ax[0].axis([-4, 4, -3, 3])
ax[1].scatter(X2[:, 0], X2[:, 1], c=y2, s=50,
cmap='viridis', norm=pts.norm)
ax[1].axis([-4, 4, -3, 3])
# format plots
format_plot(ax[0], 'Unknown Data')
format_plot(ax[1], 'Predicted Labels')
fig.savefig('E:\practice\python\代码练习\Python数据科学\机器学习\\05.01-regression-4.png')
这个方法的真实价值在于,它们可以直截了当地处理包含大量特征的数据集。
一些重要的回归算法:线性回归、支持向量机以及随机森林回归。
1.2.3、聚类:为无标签数据添加标签
前面介绍的回归与分类示例都是有监督学习算法,需要建立一个模型来预测新数据的标签。无监督学习涉及的模型将探索没有任何已知标签的数据。
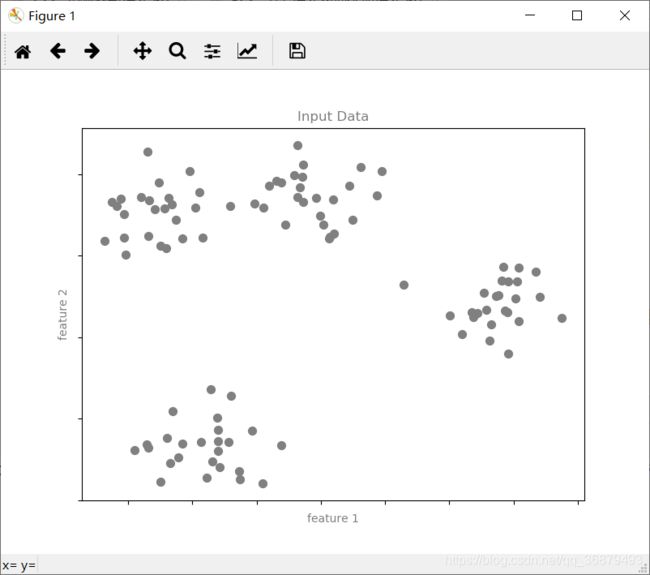
无监督学习的普遍应用之一就是 “聚类”——数据被聚类算法自动分成若干离散的组别。例如,我们有一组二维数据:
from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import KMeans
# create 50 separable points
X, y = make_blobs(n_samples=100, centers=4,
random_state=42, cluster_std=1.5)
# Fit the K Means model
model = KMeans(4, random_state=0)
y = model.fit_predict(X)
# plot the input data
fig, ax = plt.subplots(figsize=(8, 6))
ax.scatter(X[:, 0], X[:, 1], s=50, color='gray')
# format the plot
format_plot(ax, 'Input Data')
fig.savefig('E:\practice\python\代码练习\Python数据科学\机器学习\\05.01-clustering-1.png')
仅通过肉眼观察,就可以很清楚地判断出这些点应该归于哪个组。一个聚类模型会根据输入数据的固有结构判断数据点之间的相关性。通过最快、最直观的 k-means 聚类算法,就可以发现如下的类簇:
# plot the data with cluster labels
fig, ax = plt.subplots(figsize=(8, 6))
ax.scatter(X[:, 0], X[:, 1], s=50, c=y, cmap='viridis')
# format the plot
format_plot(ax, 'Learned Cluster Labels')
fig.savefig('E:\practice\python\代码练习\Python数据科学\机器学习\\05.01-clustering-2.png')
k-means 会拟合出一个由 k 个簇中心构成的模型,最优的簇中心点需要满足簇中的每个点到中心的总距离最短。显然,在二维平面上用聚类算法显然非常幼稚,但随着数据量越来越大、维度越来越多,聚类算法对于探索数据集的信息会变得十分有效。
其他重要的聚类算法:高斯混合模型和谱聚类。
1.2.4、降维:推断无标签数据的结构
降维是另一种无监督算法示例,需要从数据集本身的结构推断标签和其他信息。虽然降维比之前看到的示例要抽象些,但是一般来说,降维其实就是在保证高维数据质量的条件下从中抽取出一个低维的数据集。不同的降维算法用不同的方式衡量降维质量。
下面用一个示例进行演示:
from sklearn.datasets import make_swiss_roll
# make data
X, y = make_swiss_roll(200, noise=0.5, random_state=42)
X = X[:, [0, 2]]
# visualize data
fig, ax = plt.subplots()
ax.scatter(X[:, 0], X[:, 1], color='gray', s=30)
# format the plot
format_plot(ax, 'Input Data')
fig.savefig('E:\practice\python\代码练习\Python数据科学\机器学习\\05.01-dimesionality-1.png')
从图中可以清晰地看出数据存在某种结构:这些数据点在二维平面上按照一维螺旋线整齐地排列。从某种程度上,你可以说这些数据 “本质上” 只有一维,虽然这个一维数据是嵌在高维数据空间里的。适合这个示例的降维模型不仅需要满足数据的非线性嵌套结构,而且还要给出表现形式。
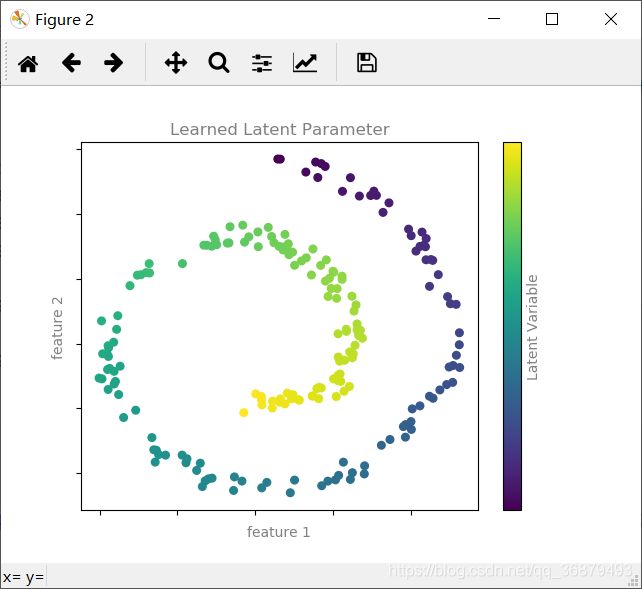
下图是通过 Isomap 算法得到的可视化结果,它是一种专门用于解决这类问题的流形学习算法:
from sklearn.manifold import Isomap
model = Isomap(n_neighbors=8, n_components=1)
y_fit = model.fit_transform(X).ravel()
# visualize data
fig, ax = plt.subplots()
pts = ax.scatter(X[:, 0], X[:, 1], c=y_fit, cmap='viridis', s=30)
cb = fig.colorbar(pts, ax=ax)
# format the plot
format_plot(ax, 'Learned Latent Parameter')
cb.set_ticks([])
cb.set_label('Latent Variable', color='gray')
fig.savefig('E:\practice\python\代码练习\Python数据科学\机器学习\\05.01-dimesionality-2.png')
一些重要的降维算法:主成分分析和各种流形学习算法,如:Isomap 算法、局部线性嵌入算法。
1.3、小结
前面介绍的主要内容包括:
-
有监督学习
可以训练带标签的数据以及预测新数据标签的模型。
-
分类
可以预测两个或多个离散分类标签的模型。
-
回归
可以预测连续标签的模型。
-
无监督学习
识别无标签数据结构的模型。
-
聚类
检测、识别数据显著组别的模型。
-
降维
从高维数据中检测、识别低维数据结构的模型。
2、Scikit-Learn 简介
2.1、Scikit-Learn 的数据表示
机器学习是从数据创建模型的学问,因此你首先需要了解怎样表示数据才能让计算机理解。Scikit-Learn 认为数据表示最好的办法就是用数据表的形式。
2.1.1、数据表
基本的数据表就是二维网格数据,其中每一行表示数据集中的每个样本,而列表示构成每个样本的相关特征。我们用 Seaborn 程序库下载数据并加载到 Pandas 的 DataFrame 中:
import seaborn as sns
iris = sns.load_dataset('iris')
print(iris.head())
'''
sepal_length sepal_width petal_length petal_width species
0 5.1 3.5 1.4 0.2 setosa
1 4.9 3.0 1.4 0.2 setosa
2 4.7 3.2 1.3 0.2 setosa
3 4.6 3.1 1.5 0.2 setosa
4 5.0 3.6 1.4 0.2 setosa
'''
其中的每行数据表示每朵被观察的鸢尾花,行数表示数据集中记录的鸢尾花总数。一般情况下,会将这个矩阵的行称为样本(samples),行数记为 n_samples。
同样,每列数据表示每个样本某个特征的量化值。一般情况下,会将矩阵的列称为特征(fratures),列数记为 n_features。
2.1.2、特征矩阵
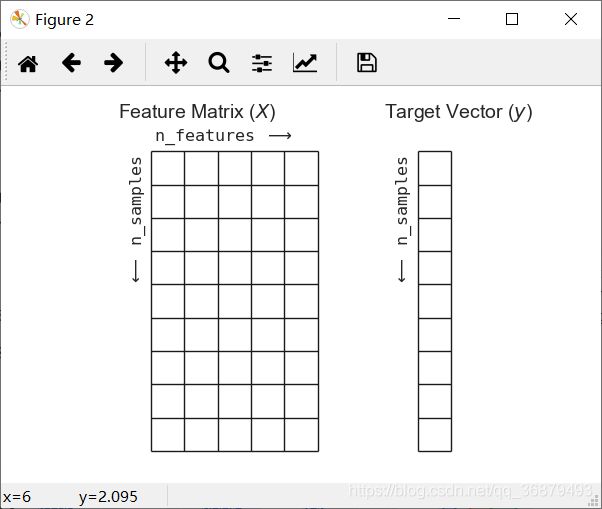
这个表格布局通过二维数组或矩阵的形式将信息清晰地表达出来,所以我们通常把这类矩阵称为特征矩阵。特征矩阵通常被简记为变量 X。它是维度为 [n_samples,n_features] 的二维矩阵,通常可以用 NumPy 数组或 Pandas 的 DataFrame 来表示,不过 Scikit-Learn 也支持 SciPy 的稀疏矩阵。
样本(即每一行)通常是指数据集中的每个对象。
特征(即每一列)通常是指每个样本都具有的某种量化观测值。一般情况下,特征都是实数,但有时也可能是布尔类型或者离散类型。
2.1.3、目标数组
除了特征矩阵 X 之外,我们还需要一个标签或目标数组,通常简记为 y。目标数组一般是一维数组,其长度就是样本总数 n_samples,通常都用一维的 NumPy 数组或 Pandas 的 Series 表示。目标数组可以是连续的数值类型,也可以是离散的类型/标签。
如何区分目标数组的特征与特征矩阵中的特征列,一直是个问题。目标数组的特征通常是我们希望从数据中预测的量化结果;借助统计学的术语,y 就是因变量。以前面的示例数据为例,我们需要通过其他测量值来建立模型,预测花的品种,而这里的 species 列就可以看成是目标数组。
知道这一列是目标数组后,就可以用 Seaborn 对数据进行可视化了:
sns.set()
sns.pairplot(iris,hue='species',size=1.5)
在使用 Scikit-Learn 之前,我们需要从 DataFrame 中抽取特征矩阵和目标数组:
X_iris = iris.drop('species',axis=1)
print(X_iris)
'''
sepal_length sepal_width petal_length petal_width
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
5 5.4 3.9 1.7 0.4
6 4.6 3.4 1.4 0.3
.. ... ... ... ...
149 5.9 3.0 5.1 1.8
[150 rows x 4 columns]
'''
y_iris = iris['species']
print(y_iris)
'''
0 setosa
1 setosa
2 setosa
3 setosa
4 setosa
5 setosa
...
149 virginica
Name: species, Length: 150, dtype: object
'''
特征矩阵和目标数组的布局如下:
fig = plt.figure(figsize=(6, 4))
ax = fig.add_axes([0, 0, 1, 1])
ax.axis('off')
ax.axis('equal')
# Draw features matrix
ax.vlines(range(6), ymin=0, ymax=9, lw=1)
ax.hlines(range(10), xmin=0, xmax=5, lw=1)
font_prop = dict(size=12, family='monospace')
ax.text(-1, -1, "Feature Matrix ($X$)", size=14)
ax.text(0.1, -0.3, r'n_features $\longrightarrow$', **font_prop)
ax.text(-0.1, 0.1, r'$\longleftarrow$ n_samples', rotation=90,
va='top', ha='right', **font_prop)
# Draw labels vector
ax.vlines(range(8, 10), ymin=0, ymax=9, lw=1)
ax.hlines(range(10), xmin=8, xmax=9, lw=1)
ax.text(7, -1, "Target Vector ($y$)", size=14)
ax.text(7.9, 0.1, r'$\longleftarrow$ n_samples', rotation=90,
va='top', ha='right', **font_prop)
ax.set_ylim(10, -2)
fig.savefig('E:\practice\python\代码练习\Python数据科学\机器学习\\05.02-samples-features.png')
2.2、Scikit-Learn 的评估器 API
Scikit-Learn 的评估器 API 主要遵循以下设计原则:
-
统一性
所有对象使用共同接口连接一组方法和统一的文档。
-
内省
所有参数值都是公共属性。
-
限制对象层级
只有算法可以用 Python 类表示。数据集都用标准数据类型(NumPy 数组、Pandas DataFrame、SciPy 稀疏矩阵)表示,参数名称用标准的 Python 字符串。
-
函数组合
许多机器学习任务都可以用一串基本算法实现,Scikit-Learn 尽力支持这种可能。
-
明智的默认值
当模型需要用户设置参数时,Scikit-Learn 预先定义适当的默认值。
Scikit-Learn 中的所有机器学习算法都是通过评估器 API 实现的,它为各种机器学习应用提供了统一的接口。
2.2.1、API 基础知识
Scikit-Learn 评估器 API 的常用步骤如下:
- 通过从 Scikit-Learn 中导入适当的评估器类,选择模型类;
- 用合适的数值对模型进行实例化,配置模型超参数(hyperparameter);
- 整理数据,通过前面介绍的方法获取特征矩阵和目标数组;
- 调用模型实例的 fit() 方法对数据进行拟合;
- 对新数据应用模型:
- 在有监督学习模型中,通常使用 predict() 方法预测新数据的标签;
- 在无监督学习模型中,通常使用 transform() 或 predict() 方法转换或推断数据的性质。
2.2.2、有监督学习示例:简单线性回归
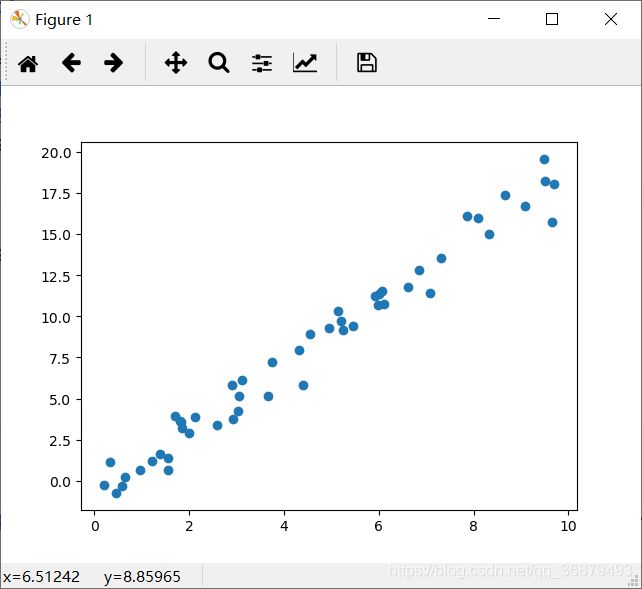
让我们来演示一个简单线性回归的建模步骤——最常见的任务就是为散点数据集(x,y)拟合一条直线。我们将使用下面的样本数据来演示这个回归示例:
import matplotlib.pyplot as plt
import numpy as np
rng = np.random.RandomState(42)
x = 10 * rng.rand(50)
y = 2 * x - 1 + rng.randn(50)
plt.scatter(x,y)
有了数据,就可以将前面介绍的步骤付诸实现了,先一步一步来:
-
选择模型类
在 Scikit-Learn 中,每个模型类都是一个 Python 类。因此,假如我们想要计算一个简单线性回归模型,那么可以直接导入线性回归模型类:
from sklearn.linear_model import LinearRegression -
选择模型超参数
请注意:模型类与模型实例不同。
当我们选择了模型类之后,还有许多参数需要配置。根据不同模型的不同情况,你可能需要回答以下问题:
- 我们想要拟合偏移量(即直线的截距)吗?
- 我们需要对模型进行归一化处理吗?
- 我们需要对特征进行预处理以提高模型灵活性吗?
- 我么打算在模型中使用哪些正则化类型?
- 我们打算使用多少模型组件?
有一些重要的参数必须在选择模型类时确定好。这些参数通常被称为超参数,即在模型拟合数据之前必须被确定的参数。在 Scikit-Learn 中,我们通常在模型初始化阶段选择超参数。
对于现在这个线性回归示例来说,可以实例化 LinearRegression 类并用 fit_intercept 超参数设置是否想要拟合直线的截距:
model = LinearRegression(fit_intercept=True) print(model) # LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)需要注意的是,对模型进行实例化其实仅仅是存储了超参数的值。我们还没有将模型应用到数据上:Scikit-Learn 的 API 对选择模型和将模型应用到数据区别得很清楚。
-
将数据整理成特征矩阵和目标数组
Scikit-Learn 的数据表示方法需要二维特征矩阵和一维目标矩阵。虽然我们的目标数组已经有了 y(长度为 n_samples 的数组),但还需要将数据 x 整理成 [n_samples,n_features] 的形式。
X = x[:,np.newaxis] print(X) ''' [[3.74540119] [9.50714306] ... [1.84854456]] ''' -
用模型拟合数据
现在就可以将模型应用到数据上了,这一步通过模型的 fit() 方法即可完成:
print(model.fit(X,y)) # LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)fit() 命令会在模型内部进行大量运算,运算结果将存储在模型属性中,供用户使用。在 Scikit-Learn 中,所有通过 fit() 方法获得的模型参数都带一条下划线。例如,在线性回归模型中,模型参数如下所示:
print(model.coef_) # [1.9776566] print(model.intercept_) # -0.9033107255311164这两个参数分别表示对样本数据拟合直线的斜率和截距。与前面样本数据的定义(斜率 2、截距 -1)进行对比,发现拟合结果与样本非常接近。
-
预测新数据的标签
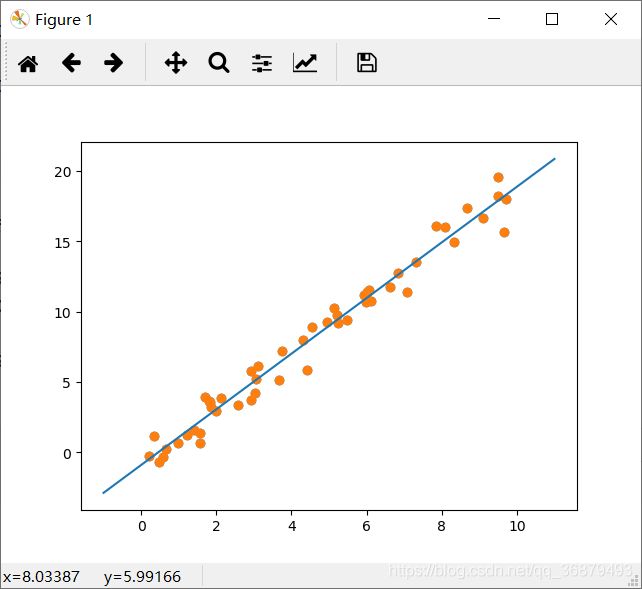
模型训练出来之后,有监督机器学习的主要任务就变成了对不属于训练集的新数据进行预测。在 Scikit-Learn 中,我们用 predict() 方法进行预测。“新数据” 是特征矩阵的 x 坐标轴,我们需要用模型预测出目标数组的 y 轴坐标:
xfit = np.linspace(-1,11)首先,将这些 x 值转换成 [n_samples,n_features] 的特征矩阵形式,之后将其输入到模型中:
Xfit = xfit[:,np.newaxis] yfit= model.predict(Xfit)最后,把原始数据和拟合结果都可视化出来:
plt.scatter(x,y) plt.plot(xfit,yfit)
2.2.3、有监督学习示例:鸢尾花数据分类
这个示例的问题是:如何为鸢尾花数据集建立模型,先用一部分数据进行训练,再用模型预测出其他样本的标签?
我们将使用非常简单的高斯朴素贝叶斯方法完成这个任务,这个方法假设每个特征中属于每一类的观测值都符合高斯分布。因为高斯朴素贝叶斯方法速度很快,而且不需要选择超参数,所以通常很适合作为初步分类手段,在借助更复杂的模型进行优化之前使用。
由于需要用模型之前没有接触过的数据评估它的训练效果,因此得先将数据分割成训练集和测试集。虽然完全可以手动实现分割数据集,但是借助 train_test_split 函数会更加方便:
from sklearn.cross_validation import train_test_split
Xtrain,Xtest,ytrain,ytest=train_test_split(X_iris,y_iris,random_state=1)
整理好数据后,用下面的模型来预测标签:
from sklearn.naive_bayes import GaussianNB # 1.选择模型类
model = GaussianNB() # 2.初始化模型
model.fit(Xtrain,ytrain) # 3.用模型拟合收数据
y_model = model.predict(Xtest) # 4.对新数据进行预测
最后,用 accuracy_score 工具验证模型预测结果的准确率(预测结果的所有结果中,正确结果占总预测样本数的比例):
from sklearn.metrics import accuracy_score
print(accuracy_score(ytest,y_model)) # 0.9736842105263158
准确率竟然高达 97%,看来即使是非常简单的分类算法也可以有效地学习这个数据集!
2.2.4、无监督学习示例:鸢尾花数据降维
对鸢尾花数据集进行降维,以便能够更方便地对数据进行可视化。前面介绍过,鸢尾花数据集由四个维度构成,即每个样本都有四个维度。
降维的任务是要找到一个可以保留数据本质特征的低维矩阵来表示高维数据。降维通常用于辅助数据可视化的工作,毕竟用二维数据画图比用四维的数据画图更方便!
下面将使用主成分分析(PCA)方法,这是一种快速线性降维技术,我们将用模型返回两个主成分,也就是用二维数据表示鸢尾花的四维数据。
同样按照前面介绍过的建模步骤进行:
from sklearn.decomposition import PCA # 1.选择模型类
model = PCA(n_components=2) # 2.初始化模型
model.fit(X_iris) # 3.用模型拟合收数据
X_2D = model.transform(X_iris) # 4.对新数据进行预测
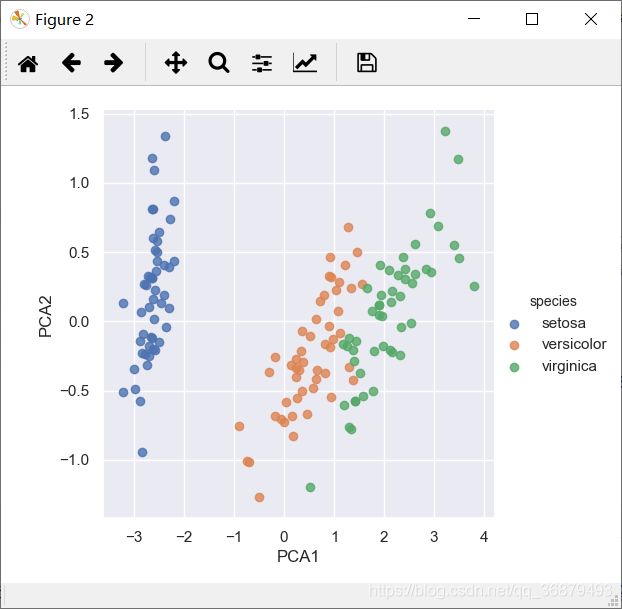
现在来画出结果。快速处理方法就是先将二维数据插入到鸢尾花的 DataFrame 中,然后用 Seaborn 的 lmplot 方法画图:
iris['PCA1'] = X_2D[:,0]
iris['PCA2'] = X_2D[:,1]
sns.lmplot('PCA1','PCA2',hue='species',data=iris,fit_reg=False
2.2.5、无监督学习示例:鸢尾花数据聚类
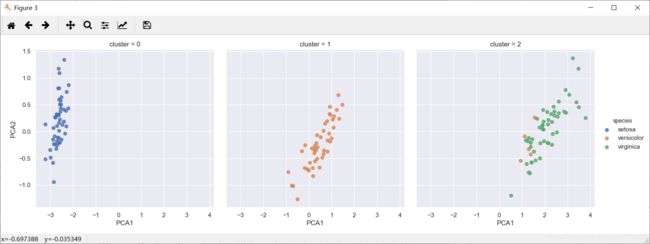
再看看如何对鸢尾花数据进行聚类,聚类算法是要对没有任何标签的数据集进行分组。我们将用一个强大的聚类方法——高斯混合模型(GMM),GMM 模型试图将数据构造成若干个服从高斯分布的概率密度函数簇。
用以下方法拟合高斯混合模型:
from sklearn.mixture import GMM # 1.选择模型类
model = GMM(n_components=3,covariance_type='full') # 2.初始化模型
model.fit(X_iris) # 3.用模型拟合收数据,不需要 y 变量
y_gmm = model.transform(X_iris) # 4.对新数据进行预测
和之前一样,将簇标签添加到鸢尾花的 DataFrame 中,然后用 Seaborn 画出结果:
iris['cluster'] = y_gmm
sns.lmplot("PCA1","PCA2",data=iris,hue='species',col='cluster',fit_reg=False)
2.3、应用:手写数字探索
2.3.1、加载并可视化手写数字
首先用 Scikit-Learn 的数据获取接口加载数据,并简单统计一下:
from sklearn.datasets import load_digits
digits = load_digits()
print(digits.images.shape) # (1797, 8, 8)
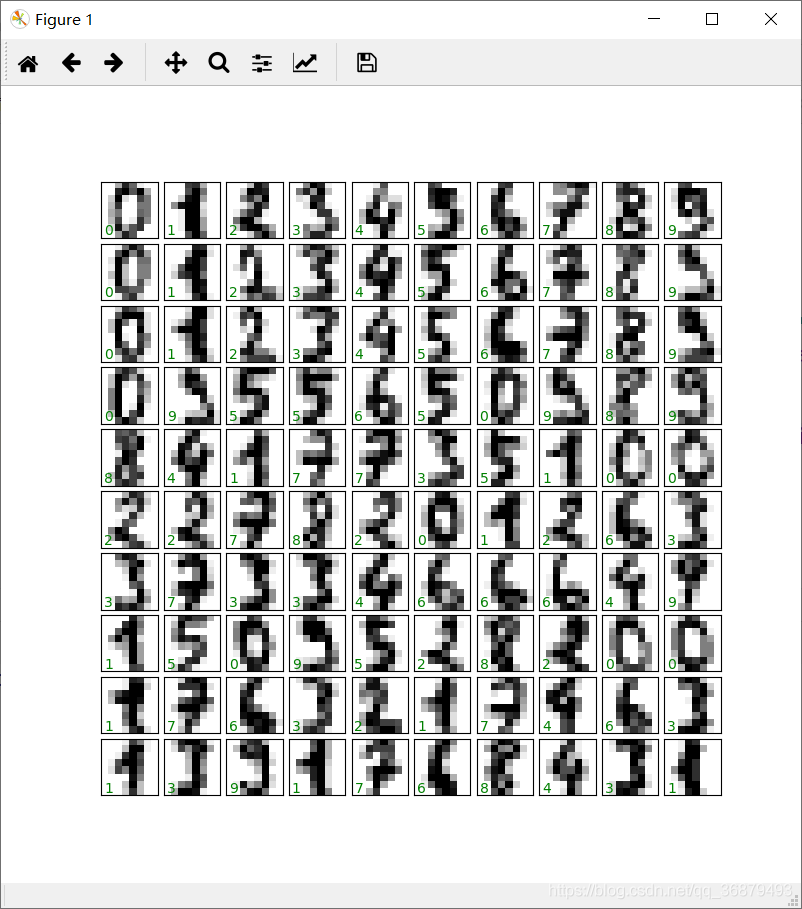
这份图像数据是一个三维矩阵:共有 1797 个样本,每张图像都是 8 像素 × 8 像素。对前 100 张图片进行可视化:
fig,axes = plt.subplots(10,10,figsize=(8,8),
subplot_kw={
'xticks':[],'yticks':[]},
gridspec_kw=dict(hspace=0.1,wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(digits.images[i],cmap='binary',interpolation='nearest')
ax.text(0.05,0.05,str(digits.target[i]),
transform=ax.transAxes,color='green')
为了在 Scikit-Learn 中使用数据,需要一个维度为 [n_samples,n_features] 的二维特征矩阵——可以将每个样本图像的所有像素都作为特征,也就是将每个数字的 8 像素 × 8 像素平铺成长度为 64 的一维数组。另外,还需要一个目标数组,用来表示每个数字的真实值(标签)。这两份数据已经放在手写数字数据集的 data 和 target 属性中,直接可以使用:
X = digits.data
print(X.shape) # (1797, 64)
y = digits.target
print(y) # (1797,)
一共有 1797 个样本和 64 个特征。
2.3.2、无监督学习:降维
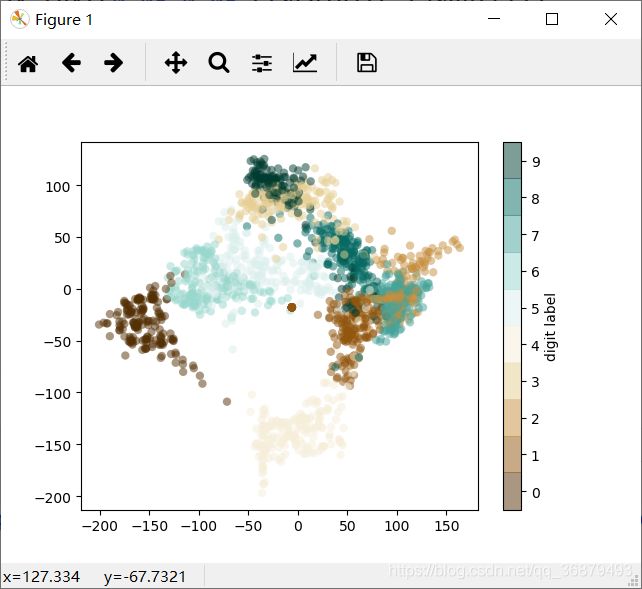
虽然我们想对具有 64 维参数空间的样本进行可视化,但是在如此高维度的空间中进行可视化十分困难。因此,我们需要借助无监督学习方法将维度降到二维。这次试试流形学习算法中的 lsomap 算法对数据进行降维:
from sklearn.manifold import Isomap
iso = Isomap(n_components=2)
iso.fit(digits.data)
data_projected = iso.transform(digits.data)
print(data_projected.shape) # (1797, 2)
现在数据已经投影到二维。把数据画出来,看看从结构中能发现什么:
plt.scatter(data_projected[:,0],data_projected[:,1],c=digits.target,
edgecolors='none',alpha=0.5,
cmap=plt.cm.get_cmap('BrBG',10))
plt.colorbar(label='digit label',ticks=range(10))
plt.clim(-0.5,9.5)
虽然有些瑕疵,但总体效果还是令人满意的。
2.3.3、数字分类
我们需要找到一个分类算法,对手写数字进行分类。和前面学习鸢尾花数据一样,先将数据分成训练集和测试集,然后用高斯朴素贝叶斯模型进行拟合:
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
model.fit(Xtrain,ytrain)
y_model = model.predict(Xtest)
模型预测已经完成,现在用模型在训练集中的正确识别样本量与总训练样本量进行对比,获得模型的准确率:
from sklearn.metrics import accuracy_score
print(accuracy_score(ytest,y_model)) # 0.8333333333333334
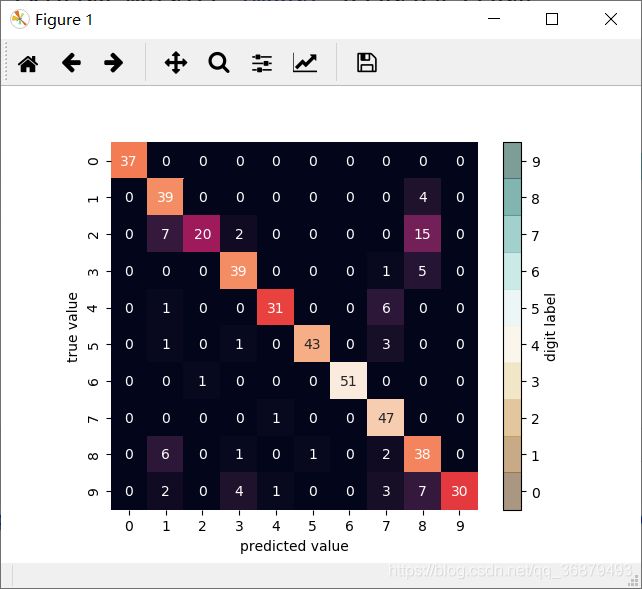
但仅依靠这个指标,我们无法知道模型哪里做得不够好,解决这个问题的方法就是用混淆矩阵。可以用 Scikit-Learn 计算混淆矩阵,然后用 Seaborn 画出来:
from sklearn.metrics import confusion_matrix
mat = confusion_matrix(ytest,y_model)
sns.heatmap(mat,square=True,annot=True,cbar=False)
plt.xlabel('predicted value')
plt.ylabel('true value')
误判的主要原因是许多数字 2 被误判为数字 1 或数组 8。另一种显示模型特征的直观方式是将样本画出来,然后把预测标签放在左下角,用绿色表示预测正确,用红色表示预测错误:
fig, axes = plt.subplots(10,10,figsize=(8,8),
subplot_kw={
'xticks':[],'yticks':[]},
gridspec_kw=dict(hspace=0.1,wspace=0.1))
test_images = Xtest.reshape(-1,8,8)
for i, ax in enumerate(axes.flat):
ax.imshow(test_images[i],cmap='binary',interpolation='nearest')
ax.text(0.05,0.05,str(y_model[i]),
transform=ax.transAxes,
color='green' if (ytest[i] == y_model[i]) else 'red')

综上,可以看到除了评估器的类型不同,导入模型 / 初始化模型 / 拟合数据 / 预测数据的步骤是完全相同的。
3、超参数与模型验证
在上一节中,我们介绍了有监督学习模型的基本步骤:
- 选择模型类;
- 选择模型超参数;
- 用模型拟合训练数据;
- 用模型预测新数据的标签。
前两步——模型选择与超参数选择——可能是有效使用各种机器学习工具和技术的最重要阶段。为了作出正确的选择,我们需要一种方法来验证选中的模型和超参数是否可以很好地拟合数据。
3.1、什么是模型验证
模型验证其实很简单,就是在选择模型和超参数之后,通过对训练数据进行学习,对比模型对已知数据的预测值与实际值的差异。
3.1.1、错误的模型验证方法
让我们再用前面介绍过的鸢尾花数据来演示一个简单的模型验证方法。首先加载数据:
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
然后选择模型与超参数。这里使用一个 k 近邻分类器,超参数为 n_neighbors = 1。这是一个非常简单直观的模型,“新数据的标签与其最接近的训练数据的标签相同”:
from sklearn.neighbors import KNeighborsClassifier
model = KNeighborsClassifier(n_neighbors=1)
然后训练模型,并用它来预测已知标签的数据:
model.fit(X,y)
y_model = model.predict(X)
最后,计算模型的准确率:
from sklearn.metrics import accuracy_score
print(accuracy_score(y,y_model)) # 1.0
准确率是 1.0,也就是说模型识别标签的正确率是 100%!但是这样测量的准确率可靠吗?答案是否定的。其实这个方法有个根本的缺陷:它用同一套数据训练和评估模型。另外,最近邻模型是一种与距离相关的评估器,只会简单地存储训练数据,然后把新数据与存储的已知数据进行对比来预测标签。在理想情况下,模型的准确率总是 100%。
3.1.2、模型验证正确方法:留出集
那怎样才能模型验证呢?其实留出集可以更好地评估模型性能,也就是说,先从训练模型的数据中流出一部分,然后用这部分留出来的数据来检验模型性能。在 Scikit-Learn 里面用 train_test_split 工具就可以实现:
from sklearn.cross_validation import train_test_split
# 每个数据集分一半数据
X1, X2, y1, y2 = train_test_split(X,y,random_state=0,train_size=0.5)
# 用模型拟合训练数据
model.fit(X1,y1)
# 在测试集中评估模型准确率
y2_model = model.predict(X2)
print(accuracy_score(y2,y2_model)) # 0.9066666666666666
3.1.3、交叉验证
用留出集进行模型验证有一个缺点,就是模型失去了一部分训练机会。解决这个问题的方法是交叉验证,也就是做一组拟合,让数据的每个子集即是训练集,又是验证集。用图形说明:
这里进行了两轮验证实验,轮流用一半数据作为留出集。如果还有前面的数据集,我们可以这样进行交叉验证:
y2_model = model.fit(X1,y1).predict(X2)
y1_model = model.fit(X2,y2).predict(X1)
print(accuracy_score(y1,y1_model),accuracy_score(y2,y2_model))
'''
0.9066666666666666
0.96 0.9066666666666666
'''
这样就可以获得两个准确率,将二者结合(例如求均值)获取一个更精确的模型总体性能。这种形式的检验被称为两轮交叉检验——将数据集分成两个子集,依次将每个子集作为验证集。
把数据分成五组,每一轮依次用模型验证拟合其中的四组数据,再预测第五组数据,评估模型准确率。用 Scikit-Learn 的 cross_val_score 函数可以非常简单地实现:
from sklearn.cross_validation import cross_val_score
print(cross_val_score(model,X,y,cv=5))
# [0.96666667 0.96666667 0.93333333 0.93333333 1. ]
对数据的不同子集重复进行交叉验证,可以让我们对算法的性能有更好的认识。
Scikit-Learn 为不同应用场景提供了各种交叉验证方法,都以迭代器形式在 cross_validation 模块实现。例如,我们可能会遇到交叉验证的轮数与样本数相同的极端情况,也就是说我们每次只有一个样本做测试,其他样本全用于训练。这种交叉验证类型被称为 LOO(leave-ine-out,只留一个)交叉验证,具体做法如下:
from sklearn.cross_validation import LeaveOneOut
scores = cross_val_score(model,X,y,cv=LeaveOneOut(len(X)))
print(scores)
'''
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1.
0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.]
'''
由于我们有 150 个样本,留一法交叉验证会生成 150 轮试验,每次试验的预测结果要么成功(得分 1.0),要么失败(得分 0.0)。计算所有试验准确率的均值就可以得到模型的预测准确率了:
print(scores.mean()) # 0.96
3.2、选择最优模型
如果模型效果不好,应该如何改善?
- 用更复杂 / 更灵活的模型;
- 用更简单 / 更确定的模型;
- 采集更多的训练样本;
- 为每个样本采集更多的特征。
3.2.1、偏差与方差的均衡
“最优模型” 的问题基本可以看成是找出偏差与方差平衡点的问题。下图显示的是对于同一数据集拟合的两种回归模型:
import numpy as np
import matplotlib.pyplot as plt
def make_data(N=30, err=0.8, rseed=1):
# randomly sample the data
rng = np.random.RandomState(rseed)
X = rng.rand(N, 1) ** 2
y = 10 - 1. / (X.ravel() + 0.1)
if err > 0:
y += err * rng.randn(N)
return X, y
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
def PolynomialRegression(degree=2, **kwargs):
return make_pipeline(PolynomialFeatures(degree),
LinearRegression(**kwargs))
X, y = make_data()
xfit = np.linspace(-0.1, 1.0, 1000)[:, None]
model1 = PolynomialRegression(1).fit(X, y)
model20 = PolynomialRegression(20).fit(X, y)
fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
ax[0].scatter(X.ravel(), y, s=40)
ax[0].plot(xfit.ravel(), model1.predict(xfit), color='gray')
ax[0].axis([-0.1, 1.0, -2, 14])
ax[0].set_title('High-bias model: Underfits the data', size=14)
ax[1].scatter(X.ravel(), y, s=40)
ax[1].plot(xfit.ravel(), model20.predict(xfit), color='gray')
ax[1].axis([-0.1, 1.0, -2, 14])
ax[1].set_title('High-variance model: Overfits the data', size=14)
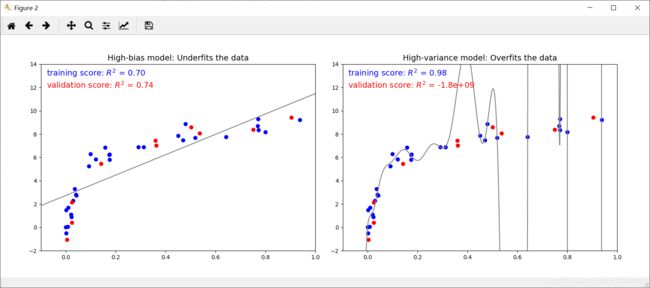
显然,这两个模型拟合得都不是很好,但它们的问题确实不一样的。
左边的模型希望从数据中找到一条直线。但由于数据本身本质上比直线要复杂,直线永远不能很好地描述这份数据。这样的模型被认为是对数据欠拟合;也就是说,模型没有足够的灵活性来适应数据的所有特征。另一种说法是模型具有高偏差。
右边的模型希望用高阶多项式拟合数据。虽然这个模型有足够的灵活性可以近乎完美的适应数据的所有特征,但与其说它是十分准确地描述了训练数据,不如说它是过多的学习了数据的噪声,而不是数据的本质属性。这样的模型被认为是对数据的过拟合,也就是模型过于灵活,在适应数据所有特征的同时,也适应了随机误差。另一种说法是模型具有高方差。
现在换个角度,如果用两个模型分别预测 y 轴的数据,看看是什么效果,下图中的浅红色点是被预测数据集遗漏的点:
fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
X2, y2 = make_data(10, rseed=42)
ax[0].scatter(X.ravel(), y, s=40, c='blue')
ax[0].plot(xfit.ravel(), model1.predict(xfit), color='gray')
ax[0].axis([-0.1, 1.0, -2, 14])
ax[0].set_title('High-bias model: Underfits the data', size=14)
ax[0].scatter(X2.ravel(), y2, s=40, c='red')
ax[0].text(0.02, 0.98, "training score: $R^2$ = {0:.2f}".format(model1.score(X, y)),
ha='left', va='top', transform=ax[0].transAxes, size=14, color='blue')
ax[0].text(0.02, 0.91, "validation score: $R^2$ = {0:.2f}".format(model1.score(X2, y2)),
ha='left', va='top', transform=ax[0].transAxes, size=14, color='red')
ax[1].scatter(X.ravel(), y, s=40, c='blue')
ax[1].plot(xfit.ravel(), model20.predict(xfit), color='gray')
ax[1].axis([-0.1, 1.0, -2, 14])
ax[1].set_title('High-variance model: Overfits the data', size=14)
ax[1].scatter(X2.ravel(), y2, s=40, c='red')
ax[1].text(0.02, 0.98, "training score: $R^2$ = {0:.2g}".format(model20.score(X, y)),
ha='left', va='top', transform=ax[1].transAxes, size=14, color='blue')
ax[1].text(0.02, 0.91, "validation score: $R^2$ = {0:.2g}".format(model20.score(X2, y2)),
ha='left', va='top', transform=ax[1].transAxes, size=14, color='red')
这个分数是 R2,也称为判定系数,用来衡量模型与目标值的对比结果。R2 = 1 表示模型与数据完全吻合,R2 = 0 表示模型不比简单取均值好,R2 为负数表示模型性能很差。从上可以得出一般的结论:
- 对于高偏差模型,模型在验证集的表现与在训练集的表现类似;
- 对于高方差模型,模型在验证集的表现远远不如在训练集的表现。
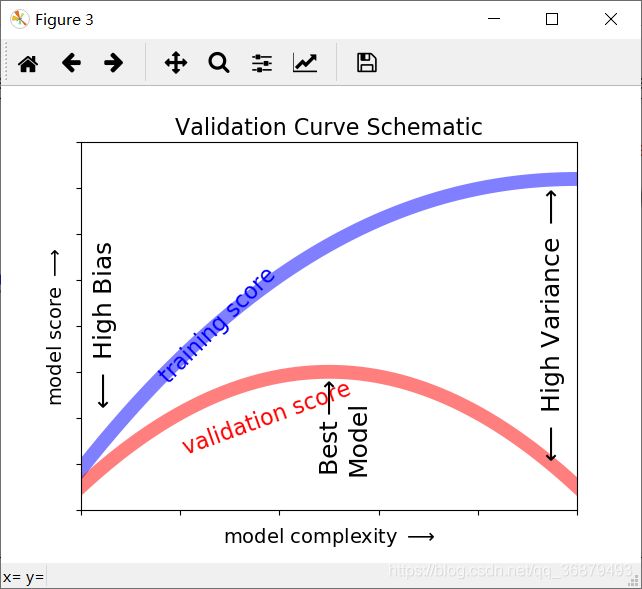
如果我们有能力不断调整模型的复杂度,那么我们可能希望训练得分和验证得分如下图:
3.2.2、Scikit-Learn 验证曲线
下面来看一个例子,用交叉验证计算一个模型的验证曲线。这里的多项式回归模型,它是线性回归模型的一般形式,其多项式的次数是一个可调参数。例如,多项式次数为 1 其实就是将数据拟合成一条直线。若模型有参数 a 和 b,则模型为:
y = a x + b y=ax+b y=ax+b
多项式系数为 3,则是将数据拟合成一条三次曲线。若模型有参数 a、b、c、d,则模型为:
y = a x 3 + b x 2 + c x + d y=ax^3+bx^2+cx+d y=ax3+bx2+cx+d
推而广之,就可以得到任意次数的多项式。在 Scikit-Learn 中,可以用一个带多项式预处理器的简单线性回归模型实现。我们将用一个管道命令来组合这两种操作:
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
def PolynomiaRegression(degree=2,**kwargs):
return make_pipeline(PolynomialFeatures(degree),
LinearRegression(**kwargs))
现在来创建一些数据给模型拟合:
import numpy as np
def make_data(N,err=1.0,rseed=1):
# 随机抽样数据
rng = np.random.RandomState(rseed)
X = rng.rand(N,1) ** 2
y = 10 - 1. / (X.ravel() + 0.1)
if err > 0:
y += err * rng.randn(N)
return X,y
X, y = make_data(40)
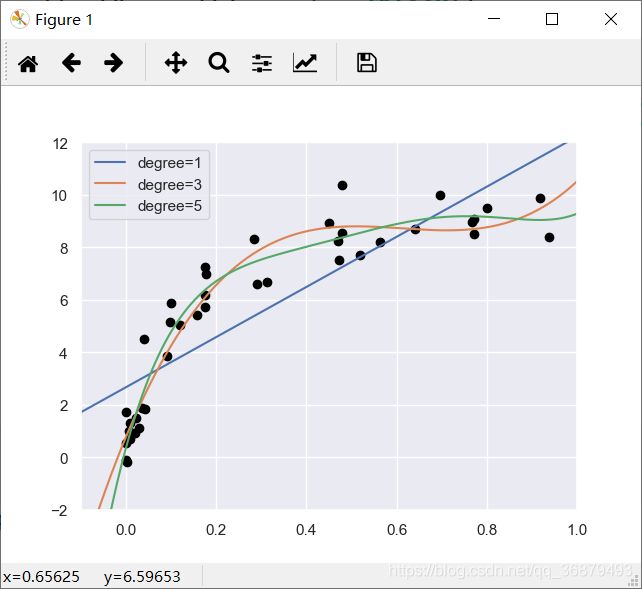
通过数据可视化,将不同次数的多项式拟合曲线画出来:
import matplotlib.pyplot as plt
import seaborn;seaborn.set() # 设置图形样式
X_test = np.linspace(-0.1,1.1,500)[:,None]
plt.scatter(X.ravel(),y,color='black')
axis = plt.axis()
for degree in [1,3,5]:
y_test = PolynomiaRegression(degree).fit(X,y).predict(X_test)
plt.plot(X_test.ravel(),y_test,label='degree={0}'.format(degree))
plt.xlim(-0.1,1.0)
plt.ylim(-2,12)
plt.legend(loc='best')
这个例子中控制模型复杂度的关键是多项式的次数,它只要是非负数即可。那么问题就来了:究竟多项式的次数是多少,才能在偏差(欠拟合)与方差(过拟合)间达到平衡?
我们可以通过多项式验证曲线来回答这个问题——利用 Scikit-Learn 的 validation_curve 函数就可以非常简单的实现。只要提供模型、数据、参数名称和验证范围信息,函数就会自动计算验证范围内的训练得分和验证得分:
from sklearn.learning_curve import validation_curve
degree = np.arange(0,21)
train_score, val_score = validation_curve(PolynomiaRegression(),X,y,
'polynomialfeatures__degree',
degree,cv=7)
plt.plot(degree,np.median(train_score,1),color='blue',label='training score')
plt.plot(degree,np.median(val_score,1),color='red',label='validation score')
plt.legend(loc='best')
plt.ylim(0,1)
plt.xlabel('degree')
plt.ylabel('score')
训练得分总是比验证得分高;训练得分随着模型复杂度的提升而单调递增;验证得分增长到最高点后由于过拟合而开始骤降。
3.3、学习曲线
影响模型复杂度的另一个重要因素是最优模型往往受到训练数据量的影响。例如,生成前面 5 倍的数据(200 个点):
X2, y2 = make_data(200)
plt.scatter(X2.ravel(),y2)
还用前面的方法画出这个大数据集验证曲线。为了对比,把之前的曲线也画出来:
degree = np.arange(21)
train_score2, val_score2 = validation_curve(PolynomiaRegression(),X2, y2,
'polynomialfeatures__degree',
degree,cv=7)
plt.plot(degree,np.median(train_score2, 1),color='blue',
label='training score')
plt.plot(degree,np.median(val_score2, 1),color='red',label='validation score')
plt.plot(degree,np.median(train_score2, 1),color='blue',alpha=0.3)
plt.legend(loc='lower center')
plt.ylim(0,1)
plt.xlabel('degree')
plt.ylabel('score')
反映训练集规模的训练得分 / 验证得分曲线被称为学习曲线。
学习曲线的特征包括以下三点:
- 特定复杂度的模型对较小的数据集容易过拟合:此时训练得分较高,验证得分较低;
- 特定复杂度的模型对较大的数据集容易欠拟合:随着数据的增大,训练得分会不断降低,而验证得分会不断升高;
- 模型的验证集得分永远不会高于训练集得分:两条曲线一直在靠近,但永远不会交叉。
学习曲线最重要的特征是,随着训练样本数量的增加,分数会收敛到定值。因此,一旦你的数据多到使模型得分已经收敛,那么增加更多的训练样本也无济于事!改善模型性能的唯一方法就是换模型(通常也是换成更复杂的模型)。
4、特征工程
机器学习实践中最重要的步骤之一是特征工程——找到与问题有关的任何信息,把它们转换成特征矩阵的数值。
4.1、分类特征
一种常见的非数值数据类型是分类数据。例如,浏览房屋数据的时候,除了看到 “房价” 和 “面积” 之类的数值特征,还会有 “地点” 信息,数据可能像这样:
data = [
{
'price':850000,'rooms':4,'neighborhood':'Queen Anne'},
{
'price':700000,'rooms':3,'neighborhood':'Fremont'},
{
'price':650000,'rooms':3,'neighborhood':'Wallingford'},
{
'price':600000,'rooms':2,'neighborhood':'Fremont'}
]
你可能会把分类特征用映射关系编码成整数:
{
'Queen Anne':1,'Fremont':2,'Wallingford':3}
但这不是一个好办法。常用的解决方法是独热编码。它可以有效增加额外的列,让 0 和 1 出现在对应的列分别表示每个分类值有或无。当你的数据像上面那样的字典列表时,用 Scikit-Learn 的 DictVectorizer 类就可以实现:
from sklearn.feature_extraction import DictVectorizer
vec = DictVectorizer(sparse=False,dtype=int)
print(vec.fit_transform(data))
'''
[[ 0 1 0 850000 4]
[ 1 0 0 700000 3]
[ 0 0 1 650000 3]
[ 1 0 0 600000 2]]
'''
你会发现,neighborhood 字段转换成了三列来表示地点标签,每一行中用 1 所在的列对应一个地点。当这些分类特征编码后,你就可以和之前一样拟合 Scikit-Learn 模型了。如果要看每一列的含义,可以用下面的代码查看特征名称:
print(vec.get_feature_names())
'''
['neighborhood=Fremont', 'neighborhood=Queen Anne', 'neighborhood=Wallingford', 'price', 'rooms']
'''
但这种方法也有一个显著的缺陷:如果你的分类特征有许多枚举值,那么数据集的维度就会急剧增加。然而,由于被编码的数据中有许多 0,因此用稀疏矩阵表示会非常高效:
vec = DictVectorizer(sparse=True,dtype=int)
print(vec.fit_transform(data))
'''
(0, 1) 1
(0, 3) 850000
(0, 4) 4
(1, 0) 1
(1, 3) 700000
(1, 4) 3
(2, 2) 1
(2, 3) 650000
(2, 4) 3
(3, 0) 1
(3, 3) 600000
(3, 4) 2
'''
4.2、文本特征
另一种常见的特征工程需求是将文本转换成一组数值。数据采集最简单的编码方法之一就是单词统计:给你基本文本,让你统计每个单词出现的次数,然后放到表格中。
例如下面三个短语:
sample = ['problem of evil',
'evil queen',
'horizon problem']
面对单词统计的数据向量化问题时,可以创建一个列来表示单词 “problem”、单词 “evil” 和单词 “horizon” 等。使用 Scikit-Learn 的 CountVectorizer 更是可以轻松实现:
from sklearn.feature_extraction.text import CountVectorizer
vec = CountVectorizer()
X = vec.fit_transform(sample)
print(X)
'''
(0, 0) 1
(0, 2) 1
(0, 3) 1
(1, 4) 1
(1, 0) 1
(2, 1) 1
(2, 3) 1
'''
结果是一个稀疏矩阵,里面记录了每个短语中每个单词的出现次数。如果用带标签的 DataFrame 来表示这个稀疏矩阵就更方便了:
import pandas as pd
print(pd.DataFrame(X.toarray(),columns=vec.get_feature_names()))
'''
evil horizon of problem queen
0 1 0 1 1 0
1 1 0 0 0 1
2 0 1 0 1 0
'''
不过这样统计也有一些问题:原始的单词统计会让一些常用词聚集太高的权重,在分类算法中这样并不合理。解决这个问题的方法就是通过 TF-IDF(词频逆文档频率),通过单词在文档中出现的频率来衡量其权重。计算这些特征的语法与之前的示例类似:
from sklearn.feature_extraction.text import TfidfVectorizer
vec = TfidfVectorizer()
X = vec.fit_transform(sample)
print(pd.DataFrame(X.toarray(),columns=vec.get_feature_names()))
'''
evil horizon of problem queen
0 0.517856 0.000000 0.680919 0.517856 0.000000
1 0.605349 0.000000 0.000000 0.000000 0.795961
2 0.000000 0.795961 0.000000 0.605349 0.000000
'''
4.3、图像特征
可以在 Scikit-Learn 项目中找到许多标准方法的高品质实现。
4.4、衍生特征
还有一种有用的特征是输入特征经过数字变换衍生出来的新特征。我们发现将一个线性回归转换成多项式回归时,并不是通过改变模型来实现的,而是通过改变输入数据!这种处理方法有时被称为基函数回归。
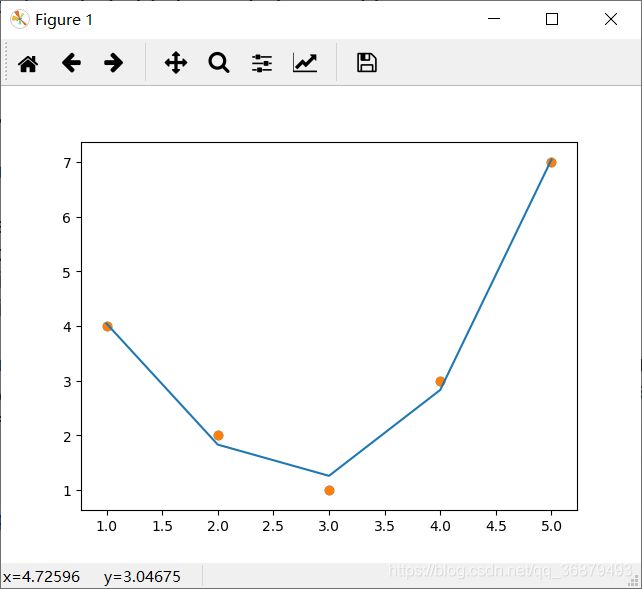
例如,下面的数据显然不能用一条直线描述:
x = np.array([1,2,3,4,5])
y = np.array([4,2,1,3,7])
plt.scatter(x,y)
但是我们仍然可以用 LinearRegression 拟合出一条直线,并获得直线的最优解:
from sklearn.linear_model import LinearRegression
X = x[:,np.newaxis]
model = LinearRegression().fit(X, y)
yfit = model.predict(X)
plt.scatter(x, y)
plt.plot(x,yfit)
很显然,我们需要用一个更复杂的模型来描述 x 与 y 的关系。可以对数据进行变换,并增加额外的特征来提升模型的复杂度。例如,可以在数据增加多项式特征:
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=3,include_bias=False)
X2 = poly.fit_transform(X)
print(X2)
'''
[[ 1. 1. 1.]
[ 2. 4. 8.]
[ 3. 9. 27.]
[ 4. 16. 64.]
[ 5. 25. 125.]]
'''
在衍生特征矩阵中,第 1 列表示 x,第 2 列表示 x2,第 3 列表示 x3。通过对这个扩展的输入矩阵计算线性回归,就可以获得更接近原始数据的结果了:
model = LinearRegression().fit(X2, y)
yfit = model.predict(X2)
plt.scatter(x, y)
plt.plot(x, yfit)
这种不通过改变模型,而是通过变换输入来改善模型效果的理念,正是许多更强大的机器学习方法的基础。基函数回归通常被认为是强大的核方法技术的驱动力之一。
4.5、缺失值填充
特征工程还有一种常见的需求就是处理缺失值。例如,有如下一个数据集:
from numpy import nan
import numpy as np
X = np.array([[nan,0,3],
[3,7,9],
[3,5,2],
[4,nan,6],
[8,8,1]])
y = np.array([14,16,-1,8,-5])
对于一般的填充方法,如均值、中位数、众数,Scikit-Learn 有 Inputer 类可以实现:
from sklearn.preprocessing import Imputer
imp = Imputer(strategy='mean')
X2 = imp.fit_transform(X)
print(X2)
'''
[[4.5 0. 3. ]
[3. 7. 9. ]
[3. 5. 2. ]
[4. 5. 6. ]
[8. 8. 1. ]]
'''
我们会发现,结果矩阵中的两处缺失值都被所在列剩余数据的均值替代了。这个被填充的数据就可以直接放到评估器里训练了,例如 LinearRegression 评估器:
from sklearn.linear_model import LinearRegression
model = LinearRegression().fit(X2, y)
print(model.predict(X2))
# [13.14869292 14.3784627 -1.15539732 10.96606197 -5.33782027]
4.6、特征管道
当你需要将多个步骤串起来时,例如:
- 用均值填充缺失值;
- 将衍生特征转换为二次方;
- 拟合线性回归模型。
为了实现这种管道处理过程,Scikit-Learn 提供了一个管道对象,如下:
model = make_pipeline(Imputer(strategy='mean'),
PolynomialFeatures(degree=2),
LinearRegression())
这个管道看起来就像一个标准的 Scikit-Learn 对象,可以对任何输入数据进行所有步骤的处理:
model.fit(X,y)
print(y) # [14 16 -1 8 -5]
print(model.predict(X)) # [14. 16. -1. 8. -5.]
这样的话,所有的步骤都会自动完成。