Python数据科学学习笔记之——机器学习专题
机器学习专题
1、专题:朴素贝叶斯分类
1.1、朴素贝叶斯分类
朴素贝叶斯分类器建立在贝叶斯分类方法的基础上,其数学基础是贝叶斯定理——一个描述统计量条件概率关系的公式。在贝叶斯分类中,我们希望确定一个具有某些特征的样本属于某类标签的概率,通常记为 P(L|特征)。贝叶斯定理告诉我们,可以直接用下面的公式计算这个概率:
P ( L ∣ 特 征 ) = P ( 特 征 ∣ L ) P ( L ) P ( 特 征 ) P(L|特征)=\frac{P(特征|L)P(L)}{P(特征)} P(L∣特征)=P(特征)P(特征∣L)P(L)
假如需要确定两种标签,定义为 L1 和 L2,一种方法就是计算这两个标签的后验概率的比值:
P ( L 1 ∣ 特 征 ) P ( L 2 ∣ 特 征 ) = P ( 特 征 ∣ L 1 ) P ( L 1 ) P ( 特 征 ∣ L 2 ) P ( L 2 ) \frac{P(L_1|特征)}{P(L_2|特征)}=\frac{P(特征|L_1)P(L_1)}{P(特征|L_2)P(L_2)} P(L2∣特征)P(L1∣特征)=P(特征∣L2)P(L2)P(特征∣L1)P(L1)
现在需要一种模型,帮助我们计算每个标签的 P(特征|Li)。这种模型被称为生成模型,因为它可以训练出生成输入数据的假设随机过程(或称为概率分布)。为每种标签设置生成模型是贝叶斯分类器训练过程的主要部分。
之所以称为 “朴素” 或 “朴素贝叶斯”,是因为如果对每种标签的生成模型进行非常简单的假设,就能找到每种类型生成模型的近似解,然后就可以使用贝叶斯分类。不同类型的朴素贝叶斯分类器是由对数据的不同假设决定的。下面将介绍一些示例来进行演示,首先导入需要用到的库:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
1.2、高斯朴素贝叶斯
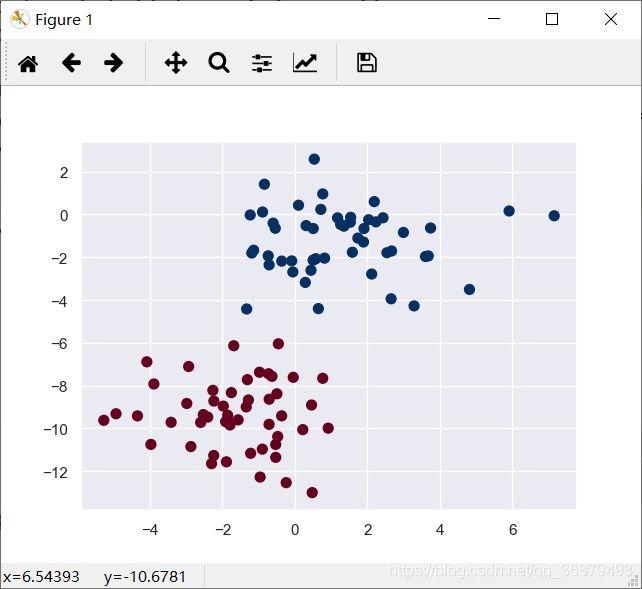
最容易理解的朴素贝叶斯分类器可能就是高斯朴素贝叶斯了,这个分类器假设每个标签的数据都服从简单的高斯分布。假如你有下面的数据:
from sklearn.datasets import make_blobs
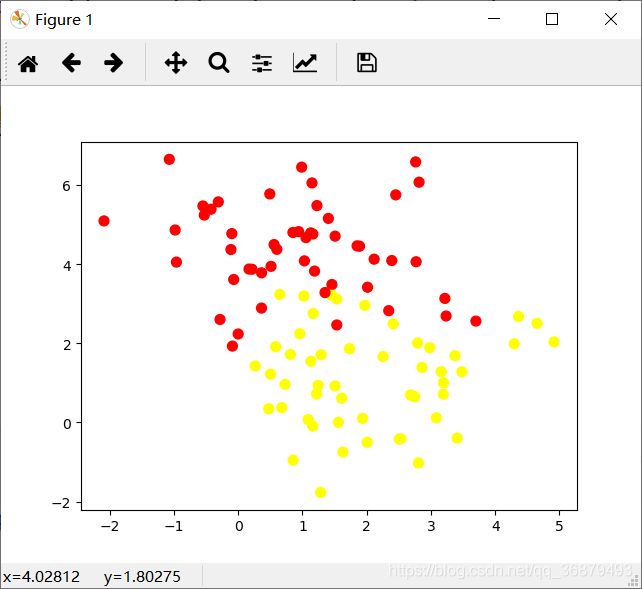
X, y = make_blobs(100, 2, centers=2, random_state=2, cluster_std=1.5)
plt.scatter(X[:,0], X[:,1], c=y, s=50, cmap='RdBu')
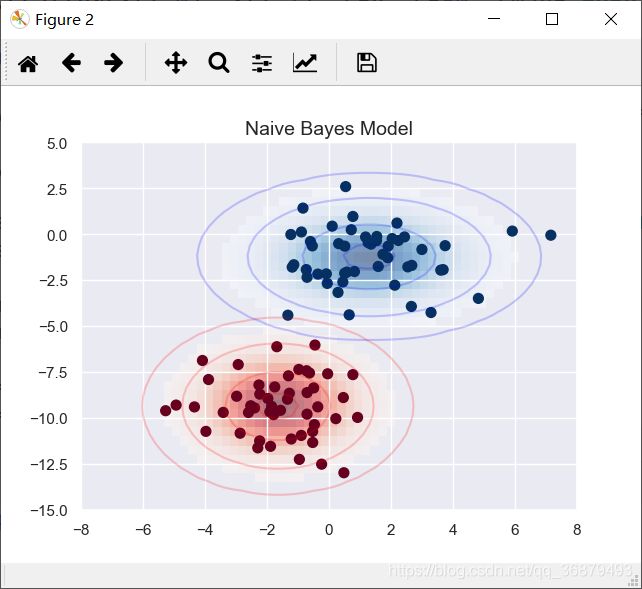
一种快速创建简易模型的方法就是假设数据服从高斯分布,且变量无协方差(指线性无关)。只有找出每个标签的所有样本点均值和标准差,再定义一个高斯分布,就可以拟合模型了。这个简单的高斯假设分类的结果如图:
from sklearn.datasets import make_blobs
X, y = make_blobs(100, 2, centers=2, random_state=2, cluster_std=1.5)
fig, ax = plt.subplots()
ax.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='RdBu')
ax.set_title('Naive Bayes Model', size=14)
xlim = (-8, 8)
ylim = (-15, 5)
xg = np.linspace(xlim[0], xlim[1], 60)
yg = np.linspace(ylim[0], ylim[1], 40)
xx, yy = np.meshgrid(xg, yg)
Xgrid = np.vstack([xx.ravel(), yy.ravel()]).T
for label, color in enumerate(['red', 'blue']):
mask = (y == label)
mu, std = X[mask].mean(0), X[mask].std(0)
P = np.exp(-0.5 * (Xgrid - mu) ** 2 / std ** 2).prod(1)
Pm = np.ma.masked_array(P, P < 0.03)
ax.pcolorfast(xg, yg, Pm.reshape(xx.shape), alpha=0.5,
cmap=color.title() + 's')
ax.contour(xx, yy, P.reshape(xx.shape),
levels=[0.01, 0.1, 0.5, 0.9],
colors=color, alpha=0.2)
ax.set(xlim=xlim, ylim=ylim)
图中的椭圆曲线表示每个标签的高斯生成模型,越靠近椭圆中心的可能性越大。通过每种类型的生成模型,可以计算出任意数据点的似然估计 P(特征|L1),然后根据贝叶斯定理计算出后验概率比值,从而确定每个数据点可能性最大的标签。
该步骤在 Scikit-Learn 的 sklearn.naive_bayes.GaussianNB 评估器中实现:
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
model.fit(X,y)
现在生成一些新数据来预测标签:
rng = np.random.RandomState(0)
Xnew = [-6,-14] + [14,18] * rng.rand(2000, 2)
ynew = model.predict(Xnew)
可以将这些新数据画出来,看看决策边界的位置:
plt.scatter(X[:, 0],X[:, 1],c=y, s=50, cmap='RdBu')
lim = plt.axis()
plt.scatter(Xnew[:, 0],Xnew[:, 1],c=ynew, s=20, cmap='RdBu', alpha=0.1)
plt.axis(lim)
可以在分类结果中看到一条稍显弯曲的边界——通常,高斯朴素贝叶斯的边界是二次方曲线。
贝叶斯主义的一个优质特性是它天生支持概率分类,我们可以用 predict_proba 方法计算样本属于某个标签的概率:
yprob = model.predict_proba(Xnew)
print(yprob[-8:].round(2))
'''
[[0.89 0.11]
[1. 0. ]
[1. 0. ]
[1. 0. ]
[1. 0. ]
[1. 0. ]
[0. 1. ]
[0.15 0.85]]
'''
这个数组分别给出了前两个标签的后验概率。如果你需要评估分类器的不确定性,那么这类贝叶斯方法非常有用。
1.3、多项式朴素贝叶斯
前面介绍的高斯假设并不意味着每个标签的生成模型只能用这一种假设。还有一种常用的假设是多项式朴素贝叶斯,它假设特征是由一个简单多项式分布生成的。多项分布可以描述各种类型样本出现次数的频率,因此多项式朴素贝叶斯非常适用于描述出现次数或者出现次数比例的特征。
这个理念与前面的相同,只不过模型数据的分布不再是高斯分布,而是多项式分布。
1.3.1、案例
多项式朴素贝叶斯通常用于文本分类,其特征都是指待分类文本的单词出现次数或者频次。前面介绍过了文本特征提取的方法,这里用 20 个网络新闻组语料库的单词出现次数作为特征,演示如何使用多项式朴素贝叶斯对这些新闻组进行分类:
首先,下载数据并看看新闻组的名字:
data = fetch_20newsgroups()
print(data.target_names)
'''
['alt.atheism',
'comp.graphics',
'comp.os.ms-windows.misc',
'comp.sys.ibm.pc.hardware',
'comp.sys.mac.hardware',
'comp.windows.x',
'misc.forsale',
'rec.autos',
'rec.motorcycles',
'rec.sport.baseball',
'rec.sport.hockey',
'sci.crypt',
'sci.electronics',
'sci.med',
'sci.space',
'soc.religion.christian',
'talk.politics.guns',
'talk.politics.mideast',
'talk.politics.misc',
'talk.religion.misc']
'''
为了简化演示过程,只选择了四类新闻,下载训练集和测试集:
categories = ['talk.religion.misc','soc.religion.christian','sci.space','comp.graphics']
train = fetch_20newsgroups(subset='train',categories=categories)
test = fetch_20newsgroups(subset='test',categories=categories)
选其中一篇新闻看看:
print(train.data[5])
'''
From: [email protected] (Don McGee)
Subject: Federal Hearing
Originator: dmcgee@uluhe
Organization: School of Ocean and Earth Science and Technology
Distribution: usa
Lines: 10
Fact or rumor....? Madalyn Murray O'Hare an atheist who eliminated the
use of the bible reading and prayer in public schools 15 years ago is now
going to appear before the FCC with a petition to stop the reading of the
Gospel on the airways of America. And she is also campaigning to remove
Christmas programs, songs, etc from the public schools. If it is true
then mail to Federal Communications Commission 1919 H Street Washington DC
20054 expressing your opposition to her request. Reference Petition number
2493.
'''
为了让这些数据能用于机器学习,需要将每个字符串的内容转换成数值向量。可以创建一个管道,将 TF-IDF 向量化方法与多项式朴素贝叶斯分类器组合在一起:
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.pipeline import make_pipeline
model = make_pipeline(TfidfVectorizer(),MultinomialNB())
通过这个管道,就可以将模型应用到训练数据上,预测出每个测试数据的标签:
model.fit(train.data,train.target)
labels = model.predict(test.data)
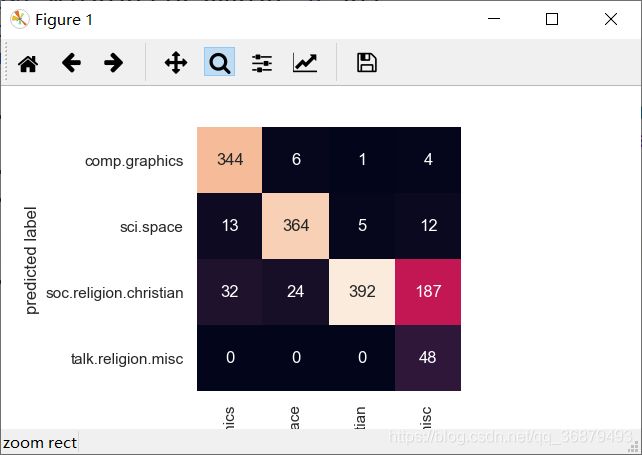
这样就得到每个测试数据的预测标签,可以进一步评估评估器的性能了。例如,用混淆矩阵统计测试数据的真实标签与预测标签的结果:
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
from sklearn.metrics import confusion_matrix
mat = confusion_matrix(test.target, labels)
sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False,
xticklabels=train.target_names,yticklabels=train.target_names)
plt.xlabel('true label')
plt.ylabel('predicted label')
可以看出,虽然用如此简单的分类器可以很好地区分关于宇宙的新闻和关于计算机的新闻,但是宗教新闻和基督教新闻的区分效果却不是很好。可能是这两个领域本身就容易混淆!
但现在我们有一个可以对任何字符串进行分类的工具了,只要用管道的 predict() 方法就可以预测。下面的函数可以快速返回字符串的预测结果:
def predict_category(s, train=train, model=model):
pred = model.predict([s])
return train.target_names[pred[0]]
下面试试模型预测结果:
print(predict_category('sending a payload to the ISS')) # sci.space
print(predict_category('discussing islam vs atheism')) # soc.religion.christian
print(predict_category('determining the screen resolution')) # comp.graphics
虽然这个分类器不会比直接用字符串内单词(加权的)频次构建的简易概率模型更复杂,但是它的分类效果却非常好。由此可见,即使是一个非常简单的算法,只要能合理利用并进行大量高维数据训练,就可以获得意想不到的效果。
1.4、朴素贝叶斯的应用场景
由于朴素贝叶斯分类器对数据有严格的假设,因此它的训练效果通常比复杂模型的差。其优点主要体现在以下四个方面:
- 训练和预测的速度非常快;
- 直接使用概率预测;
- 通常很容易解释;
- 可调参数(如果有的话)非常少;
这些优点使得朴素贝叶斯分类器通常很适合作为分类的初始解。如果分类效果满足要求,那么你将获得一个非常快速且容易解释的分类器。但如果分类效果不够好,那么你可以尝试更复杂的分类模型,与朴素贝叶斯分类器的分类效果进行对比,看看复杂模型的分类效果究竟如何。
朴素贝叶斯分类器非常适合用于以下应用场景:
- 假设分布函数与数据匹配(实际中很少见);
- 各种类型的区分度很高,模型复杂度不重要;
- 非常高维度的数据,模型复杂度不重要。
2、专题:线性回归
如果说朴素贝叶斯是解决分类任务的好起点,那么线性回归模型就是解决回归任务的好起点。
首先导入常用的程序库:
import matplotlib.pyplot as plt
import seaborn as sns;sns.set()
import numpy as np
2.1、简单线性回归
首先来介绍最广为人知的线性回归模型——将数据拟合成一条直线。直线拟合的模型方程为 y = ax + b。其中 a 是直线斜率,b 是直线截距。
看看下面的数据,它们是从斜率为 2、截距为 -5 的直线中抽取的散点:
rng = np.random.RandomState(1)
x = 10 * rng.rand(50)
y = 2 * x - 5 + rng.randn(50)
plt.scatter(x,y)
可以用 Scikit-Learn 的 LinearRegression 评估器来拟合数据,并获得最佳拟合直线:
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=True)
model.fit(x[:,np.newaxis],y)
xfit = np.linspace(0,10,1000)
yfit = model.predict(xfit[:,np.newaxis])
plt.scatter(x, y)
plt.plot(xfit, yfit)
数据的斜率和截距都在模型的拟合参数中,Scikit-Learn 通常会在参数后面加上一条下划线,即 coef_ 和 intercept_:
print("Model slope: ",model.coef_[0]) # Model slope: 2.027208810360695
print("Model intercept: ",model.intercept_) # Model intercept: -4.998577085553202
可以看到,拟合结果与真实值非常接近,这正是我们想要的。
然而,LinearRegression 评估器能做的可远不止这些——除了简单的直线拟合,它还可以处理多维度的线性回归模型:y = a0 + a1x + a2x + … 里面有多个 x 变量。从几何学的角度看,这个模型是拟合三维空间中的一个平面,或者是为更高维度的数据拟合一个超平面。
虽然这类回归模型的多维特性使得它们很难可视化,但是我们可以用 NumPy 的矩阵乘法运算符创建一些数据,从而演示这类拟合过程:
rng = np.random.RandomState(1)
X = 10 * rng.rand(100, 3)
y = 0.5 + np.dot(X, [1.5, -2, 1.])
model.fit(X, y)
print(model.intercept_) # 0.5000000000000064
print(model.coef_) # [ 1.5 -2. 1. ]
其中 y 变量是由 3 个随机的 x 变量线性组合而成,线性回归模型还原了方程的系数。
通过这种方式,就可以用一个 LinearRegression 评估器拟合数据的回归直线、平面或超平面了。虽然这种方式还是有局限性,因为它将变量限制在了线性关系上,但是不用担心,还有其他方法。
2.2、基函数回归
你可以通过基函数对原始数据进行变换,从而将变量间的线性回归模型转换为非线性回归模型。这个方法的多维建模是:
y = a 0 + a 1 x 1 + a 2 x 2 + a 3 x 3 + . . . y=a_0+a_1x_1+a_2x_2+a_3x_3+... y=a0+a1x1+a2x2+a3x3+...
其中一维的输入变量 x 转换成了三维变量 x1、x2 和 x3。让 xn = fn(x) ,这里的 fn() 是转换数据的函数。
假如 fn(x) = xn,那么模型就会变成多项式回归:
y = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + . . . y=a_0+a_1x+a_2x^2+a_3x^3+... y=a0+a1x+a2x2+a3x3+...
需要注意的是,这个模型仍然是一个线性模型,也就是说系数 an 彼此不会相乘或相除。我们其实是将一维的 x 投影到高维空间,因此通过线性模型就可以拟合出 x 与 y 之间更复杂的关系。
2.2.1、多项式基函数
多项式投影非常有用,因此 Scikit-Learn 内置了 PolynomialFeatures 转换器实现这个功能:
from sklearn.preprocessing import PolynomialFeatures
x = np.array([2, 3, 4])
poly = PolynomialFeatures(3, include_bias=False)
print(poly.fit_transform(x[:, None]))
'''
[[ 2. 4. 8.]
[ 3. 9. 27.]
[ 4. 16. 64.]]
'''
转换器通过指数函数,将一维数组转换成三维数组。这个新的高维数组之后可以放在多项式回归模型中。
最简洁的方式就是用管道实现这些功能,让我们创建一个 7 次多项式回归模型:
from sklearn.pipeline import make_pipeline
poly_model = make_pipeline(PolynomialFeatures(7),
LinearRegression())
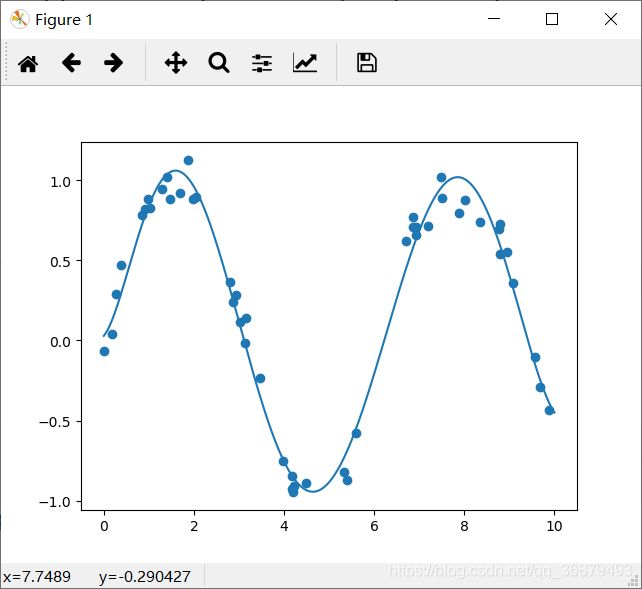
数据经过转换后,我们就可以用线性模型来拟合 x 和 y 之间更复杂的关系了。例如,下面是一条带噪声的正弦波:
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=True)
xfit = np.linspace(0,10,1000)
from sklearn.pipeline import make_pipeline
poly_model = make_pipeline(PolynomialFeatures(7),
LinearRegression())
rng = np.random.RandomState(1)
x = 10 * rng.rand(50)
y = np.sin(x) + 0.1 * rng.randn(50)
poly_model.fit(x[:, np.newaxis], y)
yfit = poly_model.predict(xfit[:, np.newaxis])
plt.scatter(x, y)
plt.plot(xfit, yfit)
通过 7 次多项式基函数,这个线性模型可以对非线性数据拟合出极好的效果!
2.2.2、高斯基函数
当然还有其他类型的基函数。例如,有一种常用的拟合模型方法使用的并不是一组多项式基函数,而是一组高斯基函数。最终结果如图:
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LinearRegression
import numpy as np
from sklearn.base import BaseEstimator, TransformerMixin
import matplotlib.pyplot as plt
class GaussianFeatures(BaseEstimator, TransformerMixin):
"""Uniformly-spaced Gaussian Features for 1D input"""
def __init__(self, N, width_factor=2.0):
self.N = N
self.width_factor = width_factor
@staticmethod
def _gauss_basis(x, y, width, axis=None):
arg = (x - y) / width
return np.exp(-0.5 * np.sum(arg ** 2, axis))
def fit(self, X, y=None):
# create N centers spread along the data range
self.centers_ = np.linspace(X.min(), X.max(), self.N)
self.width_ = self.width_factor * (self.centers_[1] - self.centers_[0])
return self
def transform(self, X):
return self._gauss_basis(X[:, :, np.newaxis], self.centers_,
self.width_, axis=1)
rng = np.random.RandomState(1)
x = 10 * rng.rand(50)
y = np.sin(x) + 0.1 * rng.randn(50)
xfit = np.linspace(0, 10, 1000)
gauss_model = make_pipeline(GaussianFeatures(10, 1.0),
LinearRegression())
gauss_model.fit(x[:, np.newaxis], y)
yfit = gauss_model.predict(xfit[:, np.newaxis])
gf = gauss_model.named_steps['gaussianfeatures']
lm = gauss_model.named_steps['linearregression']
fig, ax = plt.subplots()
for i in range(10):
selector = np.zeros(10)
selector[i] = 1
Xfit = gf.transform(xfit[:, None]) * selector
yfit = lm.predict(Xfit)
ax.fill_between(xfit, yfit.min(), yfit, color='gray', alpha=0.2)
ax.scatter(x, y)
ax.plot(xfit, gauss_model.predict(xfit[:, np.newaxis]))
ax.set_xlim(0, 10)
ax.set_ylim(yfit.min(), 1.5)
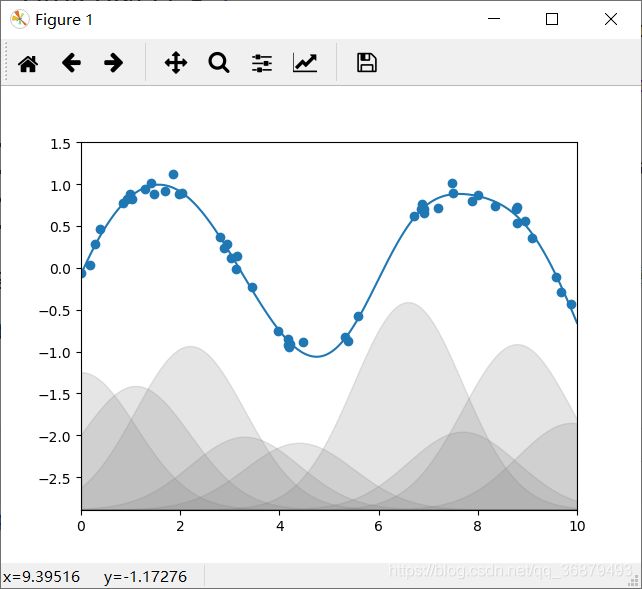
图中的阴影部分代表不同规模的基函数,把它们放在一起时就会产生平滑的曲线。Scikit-Learn 并没有内置这些高斯基函数,但我们可以自己写一个转换器来创建高斯基函数。
gauss_model = make_pipeline(GaussianFeatures(20),
LinearRegression())
gauss_model.fit(x[:,np.newaxis], y)
yfit = gauss_model.predict(xfit[:, np.newaxis])
plt.scatter(x, y)
plt.plot(xfit, yfit)
plt.xlim(0, 10)
2.2.3、正则化
引入基函数会让模型变得更加灵活,但是也很容易造成过拟合。例如,如果选择了太多高斯基函数,那么最终的拟合结果看起来可能并不好:
model = make_pipeline(GaussianFeatures(30),
LinearRegression())
model.fit(x[:, np.newaxis], y)
plt.scatter(x, y)
plt.plot(xfit, model.predict(xfit[:, np.newaxis]))
plt.xlim(0, 10)
plt.ylim(-1.5, 1.5)
如果将数据投影到 30 维的基函数上,模型就会变得过于灵活,从而能够适应数据中不同位置的异常值。如果将高斯基函数的系数画出来,就可以看到过拟合的原因:
def basis_plot(model, title=None):
fig, ax = plt.subplots(2, sharex=True)
model.fit(x[:, np.newaxis], y)
ax[0].scatter(x, y)
ax[0].plot(xfit, model.predict(xfit[:, np.newaxis]))
ax[0].set(xlabel='x', ylabel='y', ylim=(-1.5, 1.5))
if title:
ax[0].set_title(title)
ax[1].plot(model.steps[0][1].centers_,
model.steps[1][1].coef_)
ax[1].set(xlabel='basis location',
ylabel='coefficient',
xlim=(0, 10))
model = make_pipeline(GaussianFeatures(30), LinearRegression())
basis_plot(model)
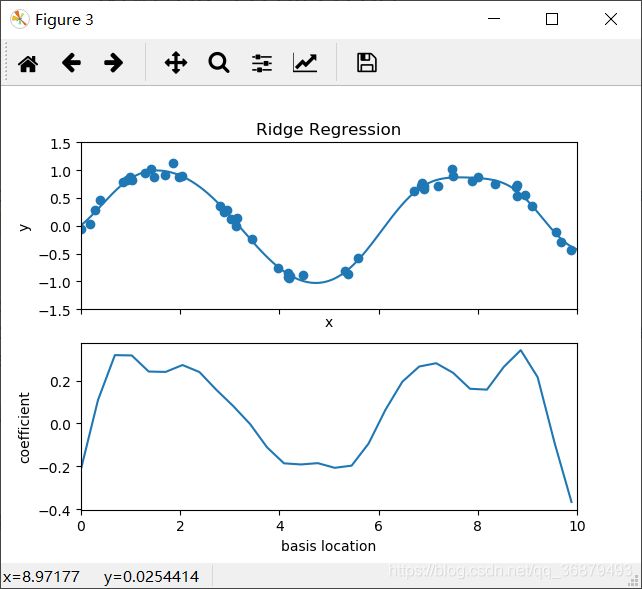
这幅图显示了每个位置上基函数的振幅。当基函数重叠时,通常就表明出现了过拟合:相邻基函数的系数相互抵消。这显然是有问题的,如果对较大的模型参数进行惩罚,从而抑制模型剧烈波动,应该就可以解决这个问题。这个惩罚机制被称为正则化,有几种不同的表现形式:
-
岭回归(L2 范数正则化)
正则化最常见的形式可能就是岭回归,有时也被称为吉洪诺夫正则化。其处理方法是对模型系数平方和(L2 范数)进行惩罚,模型拟合的惩罚项为:
P = α ∑ n = 1 N θ n 2 P=\alpha\sum_{n=1}^N \theta_n^2 P=αn=1∑Nθn2
其中,θ 是一个自由系数,用来控制惩罚力度。这种带惩罚的模型内置在 Scikit-Learn 的 Ridge 评估器中:from sklearn.linear_model import Ridge model = make_pipeline(GaussianFeatures(30),Ridge(alpha=0.1)) basis_plot(model, title='Ridge Regression')参数 α 是控制最终模型复杂度的关键。如果 α → 0,那么模型就恢复到标准线性回归结果;如果 α → ∞,那么所有模型响应都会被压制。岭回归的一个重要优点是,它可以非常高效地计算——因此相比原始的线性回归模型,几乎没有消耗更多的计算资源。
-
Lasso 正则化(L1 范数)
另一种常用的正则化被称为 Lasso,其处理方法是对模型系数绝对值的和(L1 范数)进行惩罚:
P = α ∑ n = 1 N ∣ θ n ∣ P=\alpha\sum_{n=1}^N |\theta_n| P=αn=1∑N∣θn∣
虽然和岭回归在形式上很接近,但是差别还是很大的。例如,由于其几何特性,Lasso 正则化倾向于构建稀疏模型;也就是说,它更喜欢将模型系数置为 0。from sklearn.linear_model import Lasso model = make_pipeline(GaussianFeatures(30),Lasso(alpha=0.001)) basis_plot(model, title='Lasso Regression')
3、支持向量机
支持向量机(SVM)的非常强大、灵活的有监督学习算法,既可以用于分类,也可以用来回归。
首先还是导入需要用到的库:
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# 用 Seaborn 画图
import seaborn as sns;sns.set()
3.1、支持向量机的由来
在前面介绍贝叶斯分类器时,我们首先对每个类进行了随机分布的假设,然后用生成的模型估计新数据点的标签。那是生成分类方法,这里将介绍判别分类方法;不再为每类数据建模,而是用一条分割线(二维空间中的直线或曲线)或者流形体(多维空间中的曲线、曲面等概念的推广)将各种类型分割开。
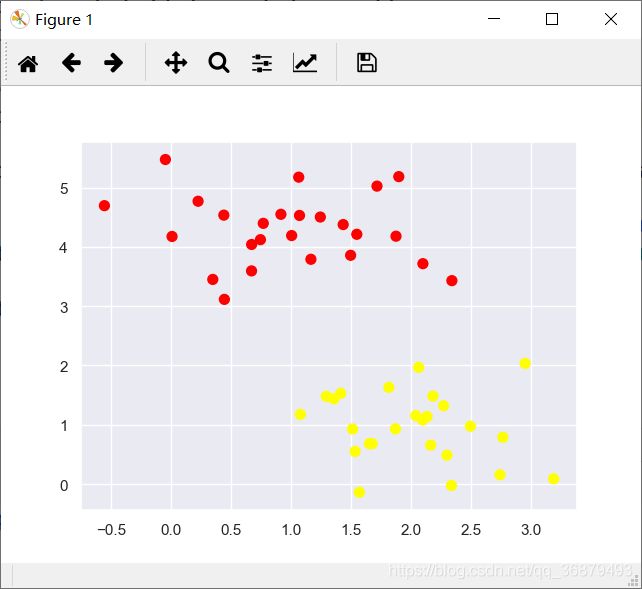
下面用一个简单的分类示例演示,其中两种类型的数据可以被清晰地分割开:
from sklearn.datasets.samples_generator import make_blobs
X, y = make_blobs(n_samples=50, centers=2,
random_state=0, cluster_std=0.60)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
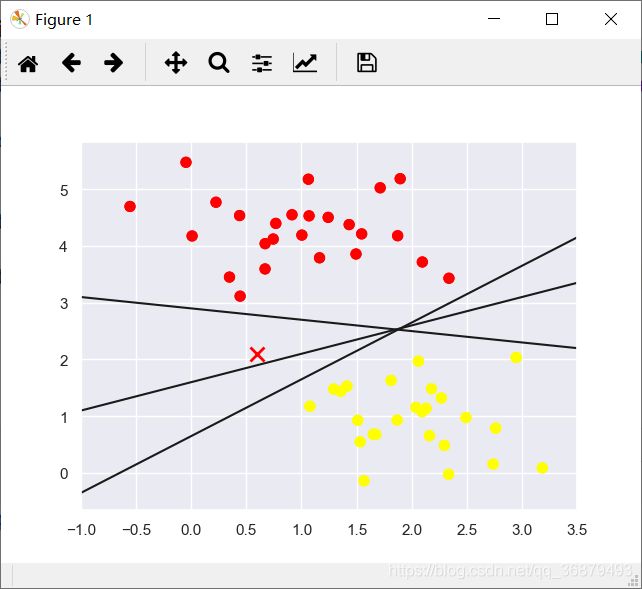
这个线性分类器尝试画一条将数据分成两部分的直线,这样就构成了一个分类模型。对于上图的二维数据来说,这个任务其实可以手动完成。但是我们马上发现一个问题:在这两种类型之间,有不止一条直线可以将它们完美分割。
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plt.plot([0.6], [2.1], 'x', color='red', markeredgewidth=2, markersize=10)
for m, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]:
plt.plot(xfit, m * xfit + b, '-k')
plt.xlim(-1, 3.5)
虽然这三个不同的分割器都能完美地判别这些样本,但是选择不同的分割线,可能会让新的数据点(图中的 “X” 点)分配到不同的标签。显然,“画一条分割不同类型的直线” 还不够,我们还需要进一步思考。
3.2、支持向量机:边界最大化
支持向量机提供了改进这个问题的办法,它直观的解释是:不再画一条细线来区分类型,而是画一条到最近点边界、有宽度的线条。具体形式如下:
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
for m, b, d in [(1, 0.65, 0.33),(0.5, 1.6, 0.55),(-0.2, 2.9, 0.2)]:
yfit = m * xfit + b
plt.plot(xfit, yfit, '-k')
plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none', color='#AAAAAA', alpha=0.4)
plt.xlim(-1, 3.5)
在支持向量机中,选择边界最大化的那条线是模型最优解。支持向量机其实就是一个边界最大化评估器。
-
拟合支持向量机
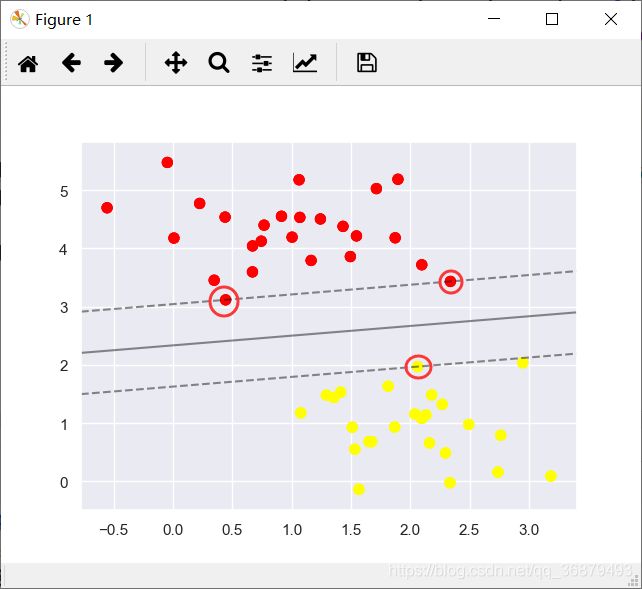
来看看这个数据的真实拟合结果:用 Scikit-Learn 的支持向量机分类器在数据上训练一个 SVM 模型。这里用一个线性核函数,并将参数 C 设置成一个很大的数:
from sklearn.svm import SVC # "Support vector classifier" model = SVC(kernel='linear', C=1E10) print(model.fit(X, y)) ''' SVC(C=10000000000.0, cache_size=200, class_weight=None, coef0=0.0, decision_function_shape='ovr', degree=3, gamma='auto', kernel='linear', max_iter=-1, probability=False, random_state=None, shrinking=True, tol=0.001, verbose=False) '''为了实现更好的可视化效果,创建一个辅助函数画出 SVM 的决策边界:
def plot_svc_decision_function(model, ax=None, plot_support=True): '''画二维 SVC 的决策函数''' if ax is None: ax = plt.gca() xlim = ax.get_xlim() ylim = ax.get_ylim() # 创建评估模型的网格 x = np.linspace(xlim[0], xlim[1], 30) y = np.linspace(ylim[0], ylim[1], 30) Y, X = np.meshgrid(y, x) xy = np.vstack([X.ravel(), Y.ravel()]).T P = model.decision_function(xy).reshape(X.shape) # 画决策边界和边界 ax.contour(X, Y, P, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--']) # 画支持向量 if plot_support: ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=300, linewidths=1, facecolors='none') ax.set_xlim(xlim) ax.set_ylim(ylim) plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn') plot_svc_decision_function(model)这就是两类数据间隔最大的分割线。你会发现有一些点正好就在边界线上。这些点是拟合的关键支持点,被称为支持向量,支持向量机算法也因为得名。在 Scikit-Learn 里面,支持向量的坐标存放在分类器的 support_vectors_ 属性中:
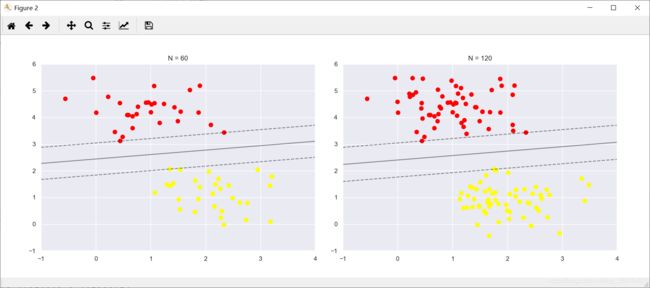
print(model.support_vectors_) ''' [[0.44359863 3.11530945] [2.33812285 3.43116792] [2.06156753 1.96918596]] '''分类器能够成功拟合的关键因素,就是这些支持向量的位置——任何在正确分类一侧远离边界线的点都不会影响拟合结果!从技术角度上讲,是因为这些点不会对拟合模型的损失函数产生任何影响,所以只要它们没有跨越边界线,它们的位置和数量就都无关紧要。例如,可以分别画出数据集前 60 个点和前 120 个点的拟合结果,并进行比较:
def plot_svm(N=10, ax=None): X, y = make_blobs(n_samples=N, centers=2, random_state=0, cluster_std=0.60) X = X[:N] y = y[:N] model = SVC(kernel='linear', C=1E10) model.fit(X, y) ax = ax or plt.gca() ax.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn') ax.set_xlim(-1, 4) ax.set_ylim(-1, 6) plot_svc_decision_function(model, ax) fig, ax = plt.subplots(1, 2, figsize=(16, 6)) fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1) for axi, N in zip(ax, [60, 120]): plot_svm(N, axi) axi.set_title('N = {0}'.format(N))我们在左图中看到的是前 60 个训练样本的模型和支持向量。在右图中,虽然我们画了前 120 个训练样本的支持向量,但是模型并没有改变:左图中的 3 个支持向量仍然适用于右图。这种对远离边界的数据点不敏感的特点正是 SVM 模型的优点之一。
-
超越线性边界:核函数 SVM 模型
将 SVM 模型与核函数组合使用,功能会非常强大。前面介绍过核函数,那时,我们将数据投影到多项式和高斯基函数定义的高维空间中,从而实现用线性分类器拟合非线性关系。
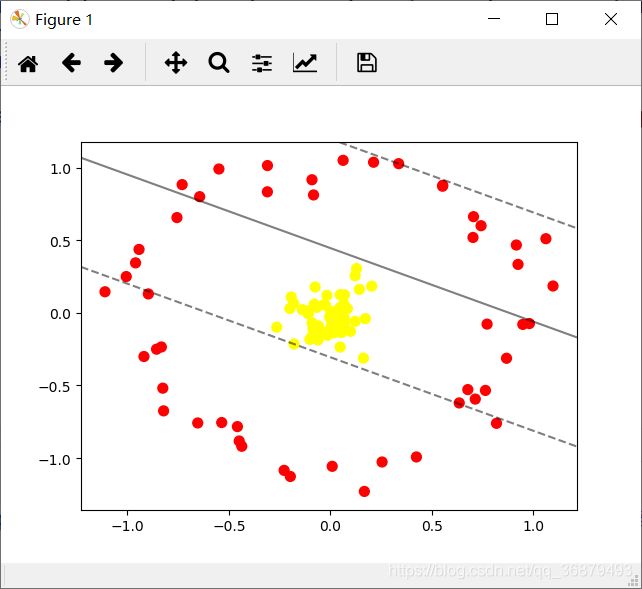
在 SVM 模型中,我们可以沿用同样的思路。为了应用核函数,引入一些非线性可分的数据:
from sklearn.datasets.samples_generator import make_circles X, y = make_circles(100, factor=.1, noise=.1) clf = SVC(kernel='linear').fit(X, y) plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn') plot_svc_decision_function(clf, plot_support=False)显然,这里需要用非线性判别方法来分割数据。将数据投影到高维空间,从而使线性分割器可以派上用场。例如,一种简单的投影方法就是计算一个以数据圆圈为中心的径向基函数:
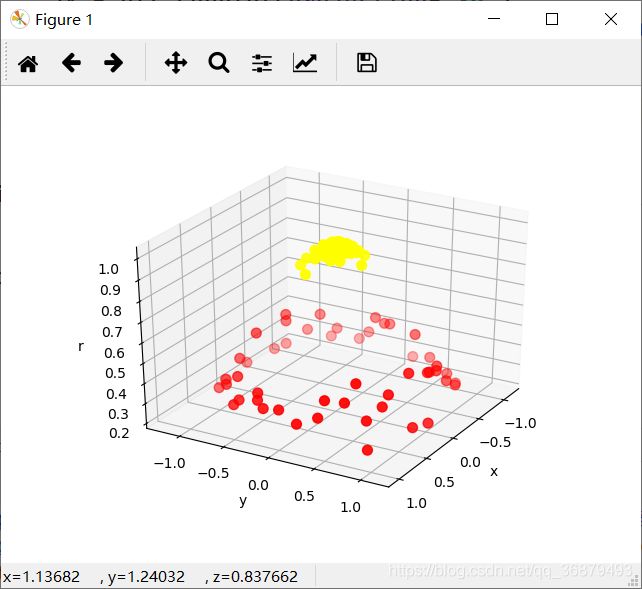
r = np.exp(-(X ** 2).sum(1))可以通过三维图来可视化新增的维度——可以用滑块变换观察角度:
from mpl_toolkits import mplot3d def plot_3D(elev=30, azim=30, X=X, y=y): ax = plt.subplot(projection='3d') ax.scatter3D(X[:, 0], X[:, 1], r, c=y, s=50, cmap='autumn') ax.view_init(elev=elev, azim=azim) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('r') interact(plot_3D(), elev=[-90, 90], azip=(-180, 180), X=fixed(X), y=fixed(y)) -
增加新维度后,数据变成了线性可分状态。如果现在画一个分割平面,例如 r = 0.7,即可将数据分割。
我们还需要仔细选择和优化投影方式;如果不能将径向基函数集中到正确的位置,那么就得不到如此干净、可分割的结果。通常,选择基函数比较困难,我们需要让模型自动指出最合适的基函数。
一种策略是计算基函数在数据集上每个点的变换结果,让 SVM 算法从所有结果中筛选出最优解。这种基函数变换方式被称为核变换,是基于每对数据点之间的相似度(或者核函数)计算的。
这种策略的问题是,如果将 N 个数据点投影到 N 维空间,当 N 不断增大的时候就会出现维度灾难,计算量巨大。但由于核函数技巧提供的小程序可以隐式计算核变换数据的拟合,也就是说,不需要建立完全的 N 维核函数投影空间!这个核函数技巧内置在 SVM 模型中,是使 SVM 方法如此强大的充分条件!
在 Scikit-Learn 里面,我们可以应用核函数化的 SVM 模型将线性核函数转变为 RBF(径向基函数)核,设置 kernel 模型超参数即可:
clf = SVC(kernel='rbf', C=1E6) print(clf.fit(X, y)) ''' SVC(C=1000000.0, cache_size=200, class_weight=None, coef0=0.0, decision_function_shape='ovr', degree=3, gamma='auto', kernel='rbf', max_iter=-1, probability=False, random_state=None, shrinking=True, tol=0.001, verbose=False) '''plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn') plot_svc_decision_function(clf) plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=300, lw=1, facecolors='none')通过使用这个核函数化的支持向量机,我们找到了一条合适的非线性决策边界。在机器学习中,核变换策略经常用于将快速线性变换成快速非线性方法,尤其是对于那些可以应用核函数技巧的模型。
-
SVM 优化:软化边界
前面的模型都是非常干净的数据集,里边都有非常完美的决策边界。但是如果有些数据会重叠怎么办?
from sklearn.datasets.samples_generator import make_blobs X, y = make_blobs(n_samples=100, centers=2, random_state=0, cluster_std=1.2) plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')为了解决这个问题,SVM 实现了一些修正因子来 “软化” 边界。为了取得更好的拟合效果,它允许一些点位于边界之内。边界线的硬度可以通过超参数进行控制,通常是 C。如果 C 很大,边界就会很硬,数据线便不能在边界内 “生存”;如果 C 比较小,边界线比较软,有一些数据就可以穿越边界线。
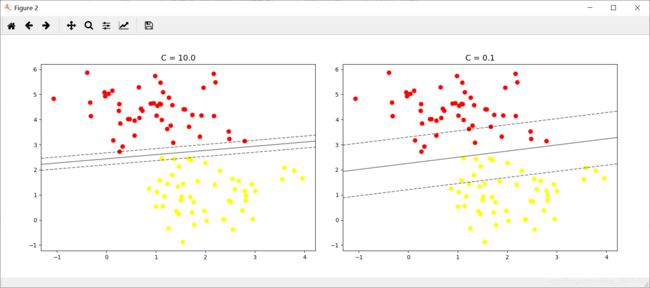
下面将演示不同参数 C 通过软化边界线,对拟合效果产生的影响:
X, y = make_blobs(n_samples=100, centers=2, random_state=0, cluster_std=0.8) fig, ax = plt.subplots(1, 2, figsize=(16, 6)) fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1) from sklearn.svm import SVC # "Support vector classifier" for axi, C in zip(ax, [10.0, 0.1]): model = SVC(kernel='linear', C=C).fit(X, y) axi.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn') plot_svc_decision_function(model, axi) axi.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=300, lw=1, facecolors='none') axi.set_title('C = {0:.1f'.format(C),size=14)参数 C 的最优值视数据集的具体情况而定,通过交叉验证或者类似的程序进行计算。
3.3、支持向量机总结
支持向量机是一种强大的分类方法,主要有四点理由:
- 模型依赖的支持向量比较少,说明它们都是非常精致的模型,消耗内存少;
- 一旦模型训练完成,预测阶段的速度非常快;
- 由于模型只受边界线附近的点的影响,因此它们对于高维度的学习效果非常好——即使训练比样本维度好高的数据也没问题,而这时其他算法难以企及的;
- 与核函数方法的配合极具通用性,能够适用不同类型的数据。
但是,SVM 模型也有一些缺点:
- 随着样本量 N 的不断增加,最差的训练时间复杂度会达到 O(N3);经过高效处理后,也只能达到 O(N2).因此,大样本学习的计算成本会非常高;
- 训练效果非常依赖边界参数 C 的选择是否合理。这需要通过交叉验证自行搜索;当数据集较大时,计算量也非常大;
- 预测结果不能直接进行概率解释。这一点可以通过内部交叉验证进行评估,但是评估过程计算量也很大。
4、决策树与随机森林
前面介绍了一个简单的分类器——朴素贝叶斯分类器,以及一个强大的判别分类器——支持向量机。下面介绍另一个强大的算法——无参数算法随机森林。随机森林是一种集成方法,通过集成多个比较简单的评估器形成累积效果。这种集成方法的学习效果往往经常出人意料,往往能超过各个组成部分的总和;也就是说,若干评估器的多数投票的最终效果往往优于单个评估器投票的结果!
导入需要用到的库:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns;sns.set()
4.1、随机森林的诱因:决策树
随机森林是建立在决策树基础上的集成学习器。因此,首先来介绍一下决策树。
决策树采用非常直观的方式对事物进行分类或打标签:你只需问一系列问题就可以记性分类了。例如,如果你想要建一棵决策树来判断旅行时遇到的一只动物的种类,你就可以提出下图的问题:
fig = plt.figure(figsize=(10, 4))
ax = fig.add_axes([0, 0, 0.8, 1], frameon=False, xticks=[], yticks=[])
ax.set_title('Example Decision Tree: Animal Classification', size=24)
def text(ax, x, y, t, size=20, **kwargs):
ax.text(x, y, t,
ha='center', va='center', size=size,
bbox=dict(boxstyle='round', ec='k', fc='w'), **kwargs)
text(ax, 0.5, 0.9, "How big is\nthe animal?", 20)
text(ax, 0.3, 0.6, "Does the animal\nhave horns?", 18)
text(ax, 0.7, 0.6, "Does the animal\nhave two legs?", 18)
text(ax, 0.12, 0.3, "Are the horns\nlonger than 10cm?", 14)
text(ax, 0.38, 0.3, "Is the animal\nwearing a collar?", 14)
text(ax, 0.62, 0.3, "Does the animal\nhave wings?", 14)
text(ax, 0.88, 0.3, "Does the animal\nhave a tail?", 14)
text(ax, 0.4, 0.75, "> 1m", 12, alpha=0.4)
text(ax, 0.6, 0.75, "< 1m", 12, alpha=0.4)
text(ax, 0.21, 0.45, "yes", 12, alpha=0.4)
text(ax, 0.34, 0.45, "no", 12, alpha=0.4)
text(ax, 0.66, 0.45, "yes", 12, alpha=0.4)
text(ax, 0.79, 0.45, "no", 12, alpha=0.4)
ax.plot([0.3, 0.5, 0.7], [0.6, 0.9, 0.6], '-k')
ax.plot([0.12, 0.3, 0.38], [0.3, 0.6, 0.3], '-k')
ax.plot([0.62, 0.7, 0.88], [0.3, 0.6, 0.3], '-k')
ax.plot([0.0, 0.12, 0.20], [0.0, 0.3, 0.0], '--k')
ax.plot([0.28, 0.38, 0.48], [0.0, 0.3, 0.0], '--k')
ax.plot([0.52, 0.62, 0.72], [0.0, 0.3, 0.0], '--k')
ax.plot([0.8, 0.88, 1.0], [0.0, 0.3, 0.0], '--k')
ax.axis([0, 1, 0, 1])
二叉树分支方法可以非常有效地进行分类:在一棵结构合理的决策树中,每个问题基本上都可以将种类可能性减半;即使是对大量种类进行决策时,也可以很快地缩小选择范围。
不过,决策树的难点在于如何设计每一步的问题。在实现决策树的机器学习算法中,问题是通常因分类边界是与特征轴平行的形式分割数据而造成的;也就是说,决策树的每个节点都根据一个特征的阈值将数据分成两组。
-
创建一棵决策树
看看下面的数据,它一共有四种标签:
from sklearn.datasets import make_blobs X, y = make_blobs(n_samples=300, centers=4, random_state=0, cluster_std=1.0) plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='rainbow')在这组数据上构建的简单决策树不断将数据的一个特征或另一个特征按照某种判定条件进行分割。每分割一次,都将新区域内点的多数投票结果标签分配到该区域上。下图展示了决策树对这组数据前四次分割的可视化结果:
from helpers_05_08 import visualize_tree from sklearn.tree import DecisionTreeClassifier from sklearn.datasets import make_blobs fig, ax = plt.subplots(1, 4, figsize=(16, 3)) fig.subplots_adjust(left=0.02, right=0.98, wspace=0.1) X, y = make_blobs(n_samples=300, centers=4, random_state=0, cluster_std=1.0) for axi, depth in zip(ax, range(1, 5)): model = DecisionTreeClassifier(max_depth=depth) visualize_tree(model, X, y, ax=axi) axi.set_title('depth = {0}'.format(depth))需要注意的是,在第一次分割之后,上半个分支里的所有数据点都没有变化,因此这个分支不需要继续分割。除非一个节点只包含一种颜色,那么每次分割都需要按照两种特征中的一种对每个区域进行分割。
如果想在 Scikit-Learn 中使用决策树拟合数据,可以用 DecisionTreeClassifier 评估器:
from sklearn.tree import DecisionTreeClassifier tree = DecisionTreeClassifier().fit(X, y)快速写一个辅助函数,对分类器的结果进行可视化:
def visualize_classifier(model, X, y, ax=None, cmap='rainbow'): ax = ax or plt.gca() # 画出训练数据 ax.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=cmap, clim=(y.min(), y.max()), zorder=3) ax.axis('tight') ax.axis('off') xlim = ax.get_xlim() ylim = ax.get_ylim() # 用评估器拟合数据 model.fit(X, y) xx, yy = np.meshgrid(np.linspace(*xlim, num=200), np.linspace(*ylim, num=200)) Z = model.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape) # 为结果生成彩色图 n_classes = len(np.unique(y)) contours = ax.contourf(xx, yy, Z, alpha=0.3, levels=np.arange(n_classes + 1) - 0.5, cmap=cmap, clim=(y.min(), y.max()), zorder=1) ax.set(xlim=xlim, ylim=ylim)现在就可以检查决策树分类的结果了:
visualize_classifier(DecisionTreeClassifier(), X, y) -
决策树与过拟合
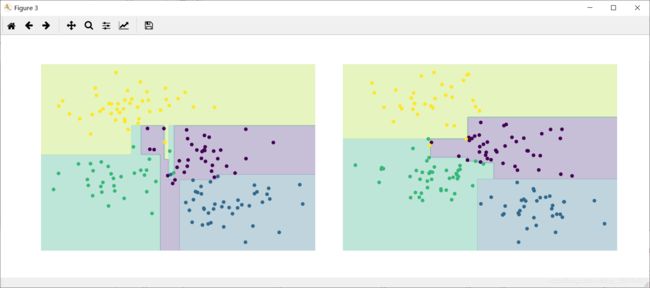
这种过拟合其实正是决策树的一般属性——决策树非常容易陷得很深,因此往往会拟合局部数据,而没有对整个数据分布的大局观。换个角度看这种过拟合,可以认为模型训练的是数据的不同子集。下图我们训练了两棵不同的决策树,每棵树拟合一半数据:
model = DecisionTreeClassifier() fig, ax = plt.subplots(1, 2, figsize=(16, 6)) fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1) visualize_tree(model, X[::2], y[::2], boundaries=False, ax=ax[0]) visualize_tree(model, X[1::2], y[1::2], boundaries=False, ax=ax[1])显然,在一些区域,两棵树产生了一致的结果;而在另一些区域,两棵树的分类结果差异就很大(例如两类接壤的区域)。不一致往往都发生在分类比较模糊的地方,因此假如将两棵树的结果组合起来,可能就会获得更好的结果。
4.2、评估器集成算法:随机森林
通过组合多个过拟合评估器来降低过拟合程度的想法其实是一种集成学习方法,称为装袋算法。装袋算法使用并行评估器对数据进行有放回抽取集成(也可以说是大杂烩),每个评估器都对数据过拟合,通过求均值可以获得更好的分类效果。随机决策树的集成算法就是随机森林。
我们可以用 Scikit-Learn 的 BaggingClassifier 元评估器来实现这种装袋分类器:
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier
tree = DecisionTreeClassifier()
bag = BaggingClassifier(tree, n_estimators=100, max_samples=0.8,
random_state=1)
visualize_classifier(bag, X, y)
在这个示例中,我们让每个评估器拟合样本 80% 的随机数。其实,如果我们用随机方法确定数据的分割方式,决策树拟合的随机性会更有效;这样做可以让所有数据在每次训练时都被拟合,但拟合的结果却仍然是随机的。
在 Scikit-Learn 里对随机决策树集成算法的优化是通过 RandomForestClassifier 评估器实现的,它会自动进行随机化决策。你只要选择一组评估器,它们就可以非常快速地完成(如果需要可以并行计算)每棵树的拟合任务:
from sklearn.ensemble import RandomForestClassifier
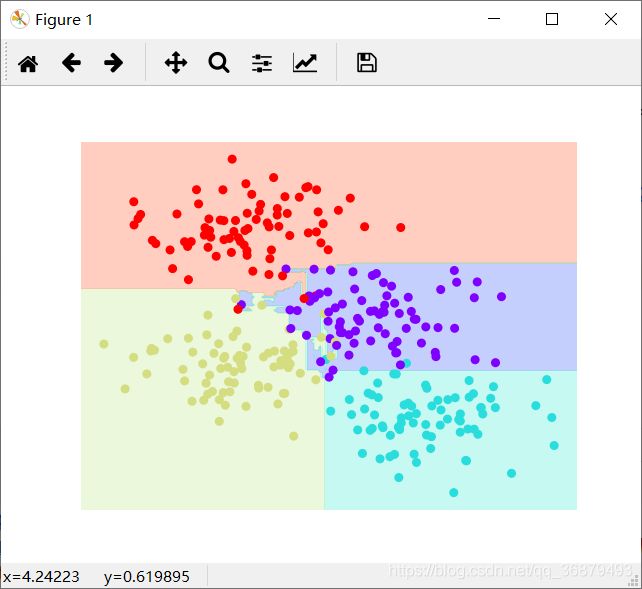
model = RandomForestClassifier(n_estimators=100, random_state=0)
visualize_classifier(model, X, y)
4.3、随机森林回归
前面介绍了随机森林分类的内容。其实随机森林也可以用作回归(处理连续变量,而不是离散变量)。随机森林回归的评估器是 RandomForestRegrssor,其语法与我们之前看到的类似。
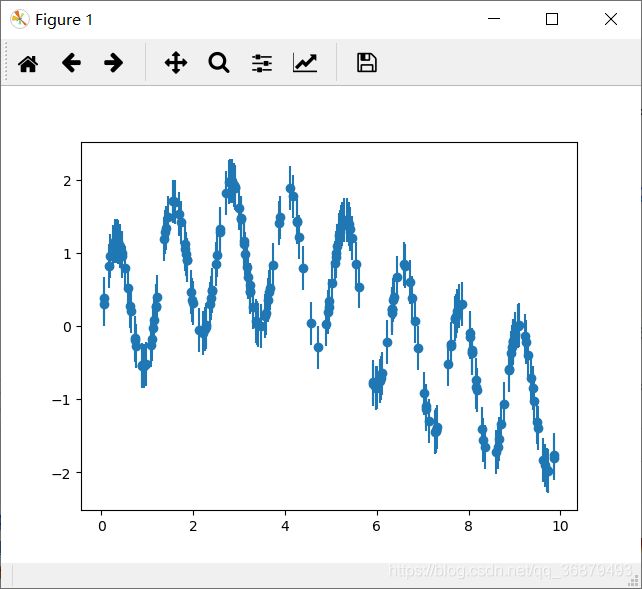
下面的数据通过快慢振荡组合而成:
rng = np.random.RandomState(42)
x = 10 * rng.rand(200)
def model(x, sigma=0.3):
fast_oscillation = np.sin(5 * x)
slow_oscillation = np.sin(0.5 * x)
noise = sigma * rng.randn(len(x))
return slow_oscillation + fast_oscillation
y = model(x)
plt.errorbar(x, y, 0.3, fmt='o')
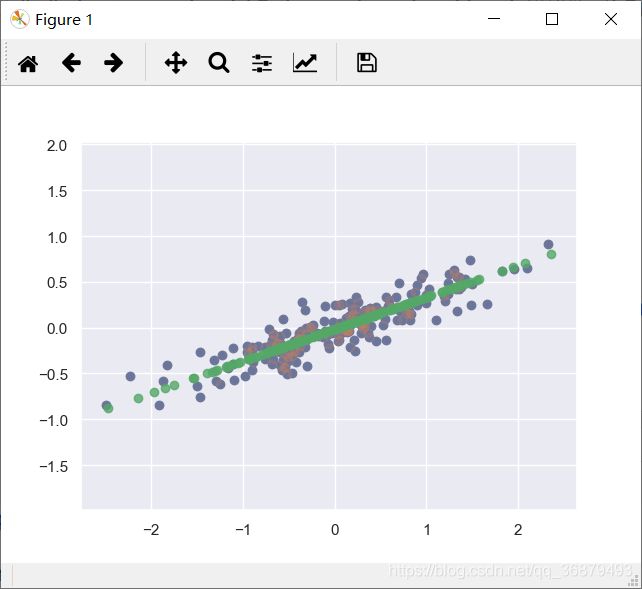
通过随机森林回归器,可以获得下面的最佳拟合曲线:
from sklearn.ensemble import RandomForestRegressor
forest = RandomForestRegressor(200)
forest.fit(x[:, None], y)
xfit = np.linspace(0, 10, 1000)
yfit = forest.predict(xfit[:, None])
ytrue = model(xfit, sigma=0)
plt.errorbar(x, y, 0.3, fmt='o', alpha=0.5)
plt.plot(xfit, yfit, '-r')
plt.plot(xfit, ytrue, '-k', alpha=0.5)
真实模型是平滑曲线,而随机森林模型是锯齿线。从图中可以看出,无参数的随机森林模型非常适合处理多周期数据,不需要我们配置多周期模型!
5、主成分分析
前面介绍了有监督评估器:这些评估器对带标签的数据进行训练,从而预测新数据的标签。后面将介绍几个无监督评估器,这些评估器可以从无标签的数据中挖掘出有趣的信息。
主成分分析(PCA)是一种非常基础的降维算法,但它仍然是一个非常有用的工具,尤其适用于数据可视化、噪音过滤、特征抽取和特征工程等。导入需要的程序包:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns;sns.set()
5.1、主成分分析简介
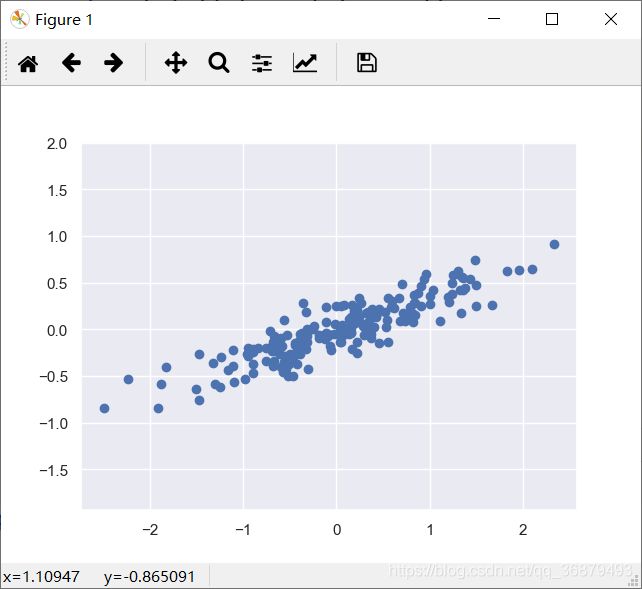
主成分分析是一个快速灵活的数据降维无监督方法。下面来可视化一个包含 200 个数据点的二维数据集,从而演示该算法的操作:
rng = np.random.RandomState(1)
X = np.dot(rng.rand(2, 2),rng.randn(2, 200)).T
plt.scatter(X[:, 0], X[:, 1])
plt.axis('equal')
从图中可以看出,x 变量与 y 变量之间具有线性关系,这让我们想起了线性回归模型。但是这里的问题稍有不同:与回归分析中希望根据 x 值预测 y 值的思路不同,无监督学习希望探索 x 值与 y 值之间的相关性。
在主成分分析中,一种量化两变量关系的方法是在数据中找到一组主轴,并用这些主轴来描述数据集。利用 Scikit-Learn 的 PCA 评估器,可以进行如下计算:
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
print(pca.fit(X))
'''
PCA(copy=True, iterated_power='auto', n_components=2, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)
'''
该拟合从数据中学习到了一些指标,其中最重要的是 “成分” 和 “可解释差异”:
print(pca.components_)
'''
[[-0.94446029 -0.32862557]
[-0.32862557 0.94446029]]
'''
print(pca.explained_variance_)
# [0.7625315 0.0184779]
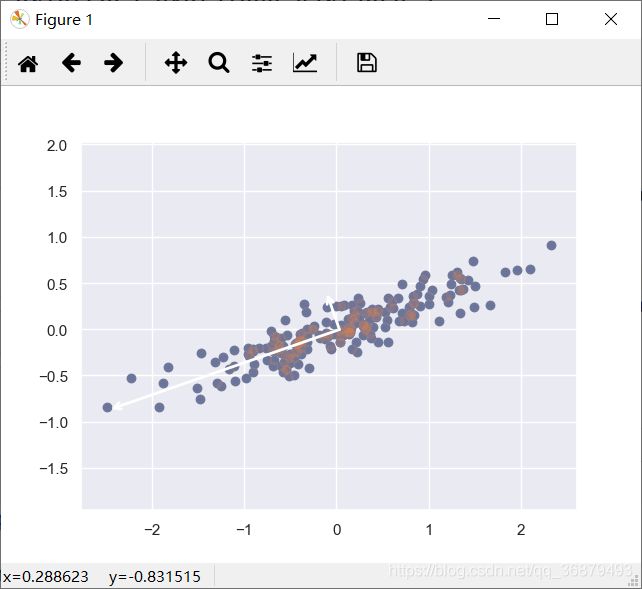
为了查看这些数字的含义,在数据图上将这些指标以向量形式画出来,用 “成分” 定义向量的方向,将 “可解释差异” 作为向量的平方长度:
def draw_vector(v0, v1, ax=None):
ax = ax or plt.gca()
arrowprops = dict(arrowstyle='->',
linewidth=2,
shrinkA=0, shrinkB=0)
ax.annotate('', v1, v0, arrowprops=arrowprops)
# 画数据
plt.scatter(X[:, 0], X[:, 1], alpha=0.2)
for length, vector in zip(pca.explained_variance_, pca.components_):
v = vector * 3 * np.sqrt(length)
draw_vector(pca.mean_, pca.mean_ + v)
plt.axis('equal')
这些向量表示数据主轴,图中箭头长度表示输入数据中各个轴的 “重要程度”——更准确的说,它衡量了数据投影到主轴上的方差的大小。每个数据点在主轴上的投影就是数据的 “主成分”。
如果将原始数据和这些主成分都画出来,将得到如下:
rng = np.random.RandomState(1)
X = np.dot(rng.rand(2, 2), rng.randn(2, 200)).T
pca = PCA(n_components=2, whiten=True)
pca.fit(X)
fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
# plot data
ax[0].scatter(X[:, 0], X[:, 1], alpha=0.2)
for length, vector in zip(pca.explained_variance_, pca.components_):
v = vector * 3 * np.sqrt(length)
draw_vector(pca.mean_, pca.mean_ + v, ax=ax[0])
ax[0].axis('equal');
ax[0].set(xlabel='x', ylabel='y', title='input')
# plot principal components
X_pca = pca.transform(X)
ax[1].scatter(X_pca[:, 0], X_pca[:, 1], alpha=0.2)
draw_vector([0, 0], [0, 3], ax=ax[1])
draw_vector([0, 0], [3, 0], ax=ax[1])
ax[1].axis('equal')
ax[1].set(xlabel='component 1', ylabel='component 2',
title='principal components',
xlim=(-5, 5), ylim=(-3, 3.1))
这种从数据的坐标轴变换到主轴的变换是一个仿射变换,仿射变换包含平移、旋转和均匀缩放三个步骤。
虽然这个寻找主成分的算法看起来就像是在解数学谜题,但是主成分分析在现实的机器学习和数据探索中有着非常广泛的应用。
-
用 PCA 降维
用 PCA 降维意味着去除一个或多个最小主成分,从而得到一个更低维度且保留最大数据方差的数据投影。
一个利用 PCA 作降维变换的示例如下:
pca = PCA(n_components=1) pca.fit(X) X_pca = pca.transform(X) print('original shape: ', X.shape) # original shape: (200, 2) print('transformed shape:', X_pca.shape) # transformed shape: (200, 1)变换的数据被投影到了单一维度。为了理解降维的效果,我们来进行数据降维的逆变换,并且与原始数据一起画出来:
X_new = pca.inverse_transform(X_pca) plt.scatter(X[:, 0], X[:, 1], alpha=0.2) plt.scatter(X_new[:, 0], X_new[:, 1], alpha=0.8) plt.axis('equal')浅色的点是原始数据,深色的点是投影的版本。我们可以很清楚地看到 PCA 降维的含义:沿着最不重要的主轴的信息都被去除了,仅留下了含有最高方差值的数据成分。被去除的那一小部分方差值(与主轴上分布的点成比例)基本上可以看成是数据在降维后损失的 “信息” 量。
这种降维后的数据集在某种程度上足以体现数据中最主要的关系:虽然有 50% 的数据维度被削减,但数据的总体关系仍然被大致保留下来。
-
用 PCA 作数据可视化:手写数字
降维的有用之处在数据仅有两个维度时可能并不是很明显,但是当数据维度很高时,它的价值就有所体现了。
下面来介绍一个将 PCA 用于手写数字数据的应用。首先导入数据:
from sklearn.datasets import load_digits digits = load_digits() print(digits.data.shape) # (1797, 64)该数据包含 8 像素 × 8 像素的图像,也就是说它是 64 维的。为了获得这些数据点间关系的直观感受,使用 PCA 将这些数据投影到一个可操作的维度,比如说二维:
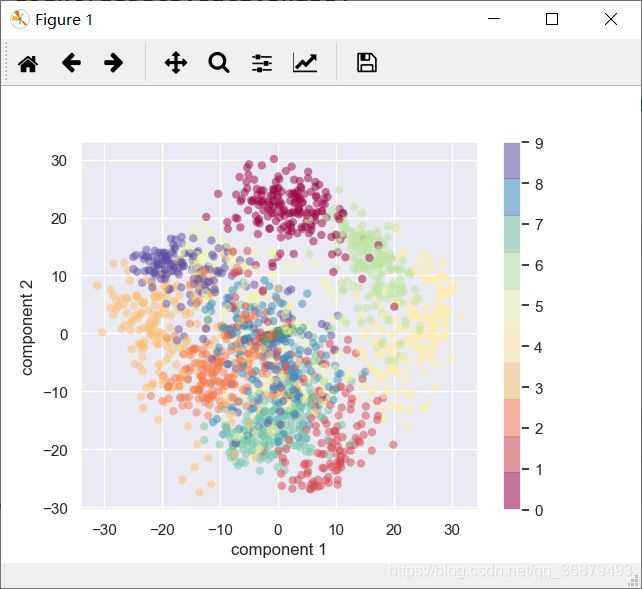
pca = PCA(2) # 从 64 维投影至二维 projected = pca.fit_transform(digits.data) print(digits.data.shape) # (1797, 64) print(projected.shape) # (1797, 2)画出每个点的前两个主成分,更好地了解数据:
plt.scatter(projected[:, 0], projected[:, 1], c=digits.target, edgecolors='none', alpha=0.5, cmap=plt.cm.get_cmap('Spectral', 10)) plt.xlabel('component 1') plt.ylabel('component 2') plt.colorbar()这些成分的含义:整个数据是一个 64 维的点云,而且这些点还是每个数据点沿着最大方差方向的投影。我们找到了在 64 维空间中最优的延伸和旋转方案,使得我们可以看到这些点在二维平面的布局。
-
成分的含义
我们进一步提出问题:削减的维度有什么含义?可以从基向量的组合角度来理解这个问题。例如,训练集中的每幅图像都是由一组 64 像素值的集合定义的,将称其为向量 x:
x = [ x 1 , x 2 , x 3 , . . . , x 64 ] x=[x_1,x_2,x_3,...,x_{64}] x=[x1,x2,x3,...,x64]
我们可以用像素的概念来理解。也就是说,为了构建一幅图像,将向量的每个元素与对应描述的像素(单位列向量)相乘,然后将这些结果加和就是这幅图像:
i m a g e ( x ) = x 1 ⋅ ( p i x e l 1 ) + x 2 ⋅ ( p i x e l 2 ) + . . . + x 64 ⋅ ( p i x e l 64 ) image(x)=x_1 \cdot (pixel \quad 1)+x_2 \cdot (pixel \quad 2)+...+x_{64} \cdot (pixel \quad 64) image(x)=x1⋅(pixel1)+x2⋅(pixel2)+...+x64⋅(pixel64)
我们可以将数据的降维理解为删除大部分元素,仅保留少量元素的基向量。例如,如果仅使用前面 8 个像素,我们会得到数据的 8 维投影(如下图)。但是它并不能反映整幅图像,因为我们丢掉了几乎 90% 的像素信息:def plot_pca_components(x, coefficients=None, mean=0, components=None, imshape=(8, 8), n_components=8, fontsize=12, show_mean=True): if coefficients is None: coefficients = x if components is None: components = np.eye(len(coefficients), len(x)) mean = np.zeros_like(x) + mean fig = plt.figure(figsize=(1.2 * (5 + n_components), 1.2 * 2)) g = plt.GridSpec(2, 4 + bool(show_mean) + n_components, hspace=0.3) def show(i, j, x, title=None): ax = fig.add_subplot(g[i, j], xticks=[], yticks=[]) ax.imshow(x.reshape(imshape), interpolation='nearest') if title: ax.set_title(title, fontsize=fontsize) show(slice(2), slice(2), x, "True") approx = mean.copy() counter = 2 if show_mean: show(0, 2, np.zeros_like(x) + mean, r'$\mu$') show(1, 2, approx, r'$1 \cdot \mu$') counter += 1 for i in range(n_components): approx = approx + coefficients[i] * components[i] show(0, i + counter, components[i], r'$c_{0}$'.format(i + 1)) show(1, i + counter, approx, r"${0:.2f} \cdot c_{1}$".format(coefficients[i], i + 1)) if show_mean or i > 0: plt.gca().text(0, 1.05, '$+$', ha='right', va='bottom', transform=plt.gca().transAxes, fontsize=fontsize) show(slice(2), slice(-2, None), approx, "Approx") return figfrom sklearn.datasets import load_digits digits = load_digits() sns.set_style('white') fig = plot_pca_components(digits.data[10], show_mean=False)面板的上面一行是单独的像素信息,下面一行是这些像素值的累加,累加值最终构成这幅图像。如果仅使用 8 个像素成分,就仅能构成这个 64 像素图像的一小部分。只有使用该序列和全部的 64 像素,才能恢复原始图像。
但是逐像素表示方法并不是选择基向量的唯一方式。我们也可以使用其他基函数,这些基函数包含预定义的每个像素的贡献,如下:
i m a g e ( x ) = m e a n + x 1 ⋅ ( b a s i s 1 ) + x 2 ⋅ ( b a s i s 2 ) + x 3 ⋅ ( b a s i s 3 ) + . . . image(x)=mean+x_1 \cdot (basis \quad 1)+x_2 \cdot (basis \quad 2)+x_3 \cdot (basis \quad 3)+... image(x)=mean+x1⋅(basis1)+x2⋅(basis2)+x3⋅(basis3)+...
PCA 可以被认为是选择最优基函数的过程,这样将这些基函数中前几个加起来就足以重构数据集中的大部分元素。用低维形式表现数据的主成分,其实就是与序列每一个元素相乘的系数。下图就是用均值加上前 8 个 PCA 基函数重构数字的效果:pca = PCA(n_components=8) Xproj = pca.fit_transform(digits.data) sns.set_style('white') fig = plot_pca_components(digits.data[10], Xproj[10], pca.mean_, pca.components_)与像素基不同,PCA 基可以通过为一个均值加上 8 个成分,来恢复输入图像最显著的特征。每个成分中像素的数量必然是二维数据示例中向量的方向。这就是 PCA 提供数据的低维表示的原理:它发现一组比原始的像素基向量更能有效的表示输入数据的基函数。
-
选择成分的数量
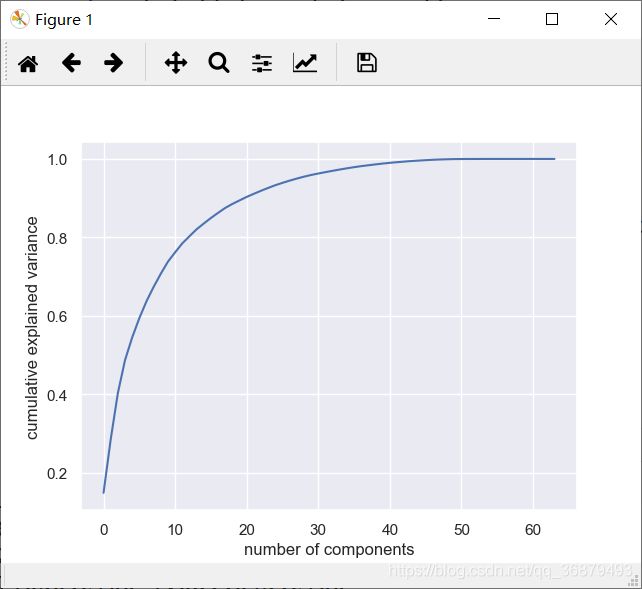
在实际使用 PCA 的过程中,正确估计用于描述数据的成分的数量是非常重要的环节。我们可以将累计方差贡献率看作是关于成分数量的函数,从而确定所需成分的数量:
pca = PCA().fit(digits.data) print(pca.explained_variance_) plt.plot(np.cumsum(pca.explained_variance_ratio_)) plt.xlabel('number of components') plt.ylabel('cumulative explained variance')这个曲线量化了前 N 个主成分中包含多少总的 64 维的方差。例如,可以看到前 10 个成分包含了几乎 75% 的方差。因此,如果你希望描述接近 100% 的方差,那么就需要大约 50 个成分。
5.2、用 PCA 作噪音过滤
PCA 也可以用作噪音数据的过滤方法——任何成分的方差都远大于噪音的方差,所以相比于噪音,成分应该相对不受影响。因此,如果你仅用主成分的最大子集重构该数据,那么应该可以实现选择性保留信号并且丢弃噪音。
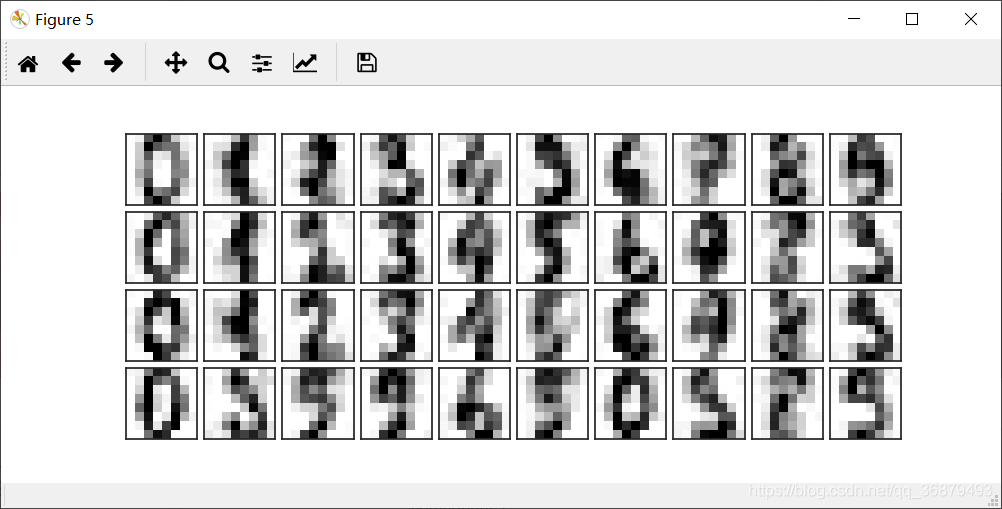
用手写数字数据看看如何实现噪音过滤。首先画出几个无噪音的输入数据:
def plot_digits(data):
fig, axes = plt.subplots(4, 10, figsize=(10, 4),
subplot_kw={
'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(data[i].reshape(8, 8),
cmap='binary', interpolation='nearest',
clim=(0, 16))
plot_digits(digits.data)
现在添加一些随机噪音并创建一个噪音数据集,重新画图:
np.random.seed(42)
noisy = np.random.normal(digits.data, 4)
plot_digits(noisy)
用噪音数据训练一个 PCA,要求投影后保存 50% 的方差:
pca = PCA(0.50).fit(noisy)
print(pca.n_components_) # 12
这里 50% 的方差对应 12 个主成分。现在来计算这些成分,然后利用逆变换重构过滤后的手写数字:
components = pca.transform(noisy)
filtered = pca.inverse_transform(components)
plot_digits(filtered)
这个信号保留 / 噪音过滤的性质使 PCA 成为一种非常有用的特征选择方式。例如,与其在很高的维度上训练分类器,你可以选择在一个低维表示中训练分类器,该分类器将自动过滤输入数据中的随机噪音。
5.3、主成分分析总结
这一节讨论了主成分分析进行降维、高维数据的可视化、噪音过滤,以及高维数据的特征选择。对于任意高维的数据集,我倾向于以 PCA 分析开始,可视化点间的关系,理解数据中的主要方差,理解固有的维度(通过画解释方差比)。
经常受数据集的异常点影响是 PCA 的主要弱点。
6、流形学习
前面介绍过如何使用主成分分析降维——它可以在减少数据集特征的同时,保留数据点间的必要性。但是主成分分析对存在非线性关系的数据集的处理效果并不好。为了弥补这个缺陷,我们选择另外一个方法——流形学习。流形学习是一种无监督评估器,它试图将一个低维度流形嵌入到一个高维度空间来描述数据集。
这里将深入介绍几种流形学习的技巧,包括多维标度法(MDS)、局部线性嵌入法(LLE)和保距映射法(Isomap)。首先还是导入标准程序库:
import matplotlib.pyplot as plt
import seaborn as sns;sns.set()
import numpy as np
6.1、流形学习:“HELLO”
先生成一些二维数据来定义一个流行。下面用函数创建一组数据,构成单词 “HELLO” 的形状:
def make_hello(N=1000, rseed=42):
# 画出 “HELLO” 文字形状的图像,并保存为 PNG
fig, ax = plt.subplots(figsize=(4, 1))
fig.subplots_adjust(left=0, right=1, bottom=0, top=1)
ax.axis('off')
ax.text(0.5, 0.4, 'HELLO', va='center', ha='center', weight='bold', size=85)
fig.savefig('hello.png')
plt.close()
# 打开这个 PNG,并将一些随机点画进去
from matplotlib.pyplot import imread
data = imread('hello.png')[::-1, :, 0].T
rng = np.random.RandomState(rseed)
X = rng.rand(4 * N, 2)
i, j = (X * data.shape).astype(int).T
mask = (data[i, j] < 1)
X = X[mask]
X[:, 0] *= (data.shape[0] / data.shape[1])
X = X[:N]
return X[np.argsort(X[:, 0])]
调用该函数并且画出结果数据:
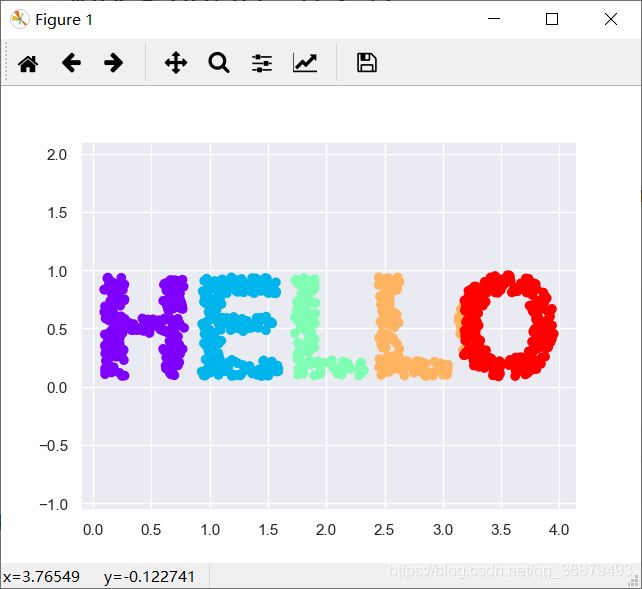
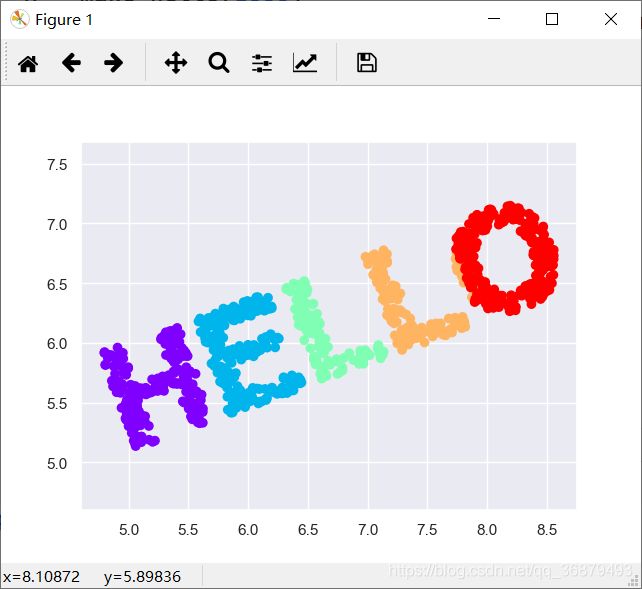
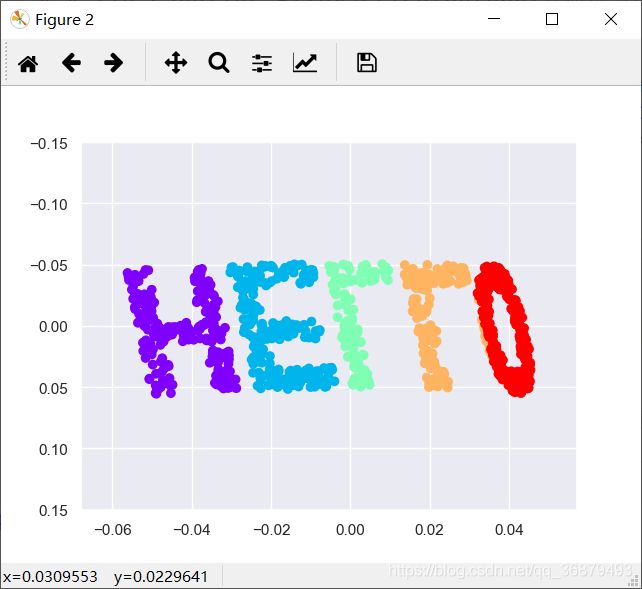
X = make_hello(1000)
colorize = dict(c=X[:, 0], cmap=plt.cm.get_cmap('rainbow', 5))
plt.scatter(X[:, 0], X[:, 1], **colorize)
plt.axis('equal')
6.2、多维标度法(MDS)
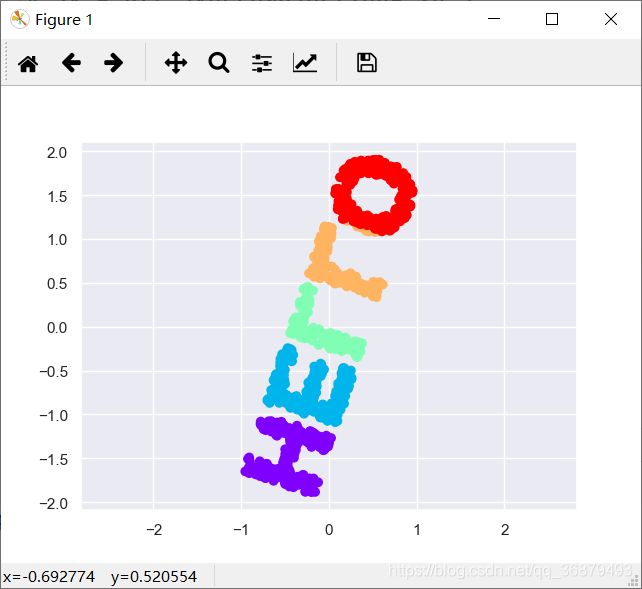
通过观察这个数据集,可以看到数据集中选中的 x 值和 y 值并不是对数据的最基本描述:即使放大、缩小或旋转数据,“HELLO” 仍然会很明显。例如,如果用一个旋转矩阵来旋转数据,x 和 y 的值将会改变,但是数据形状基本还是一样的:
def rotate(X, angle):
theta = np.deg2rad(angle)
R = [[np.cos(theta), np.sin(theta)],
[-np.sin(theta), np.cos(theta)]]
return np.dot(X, R)
X2 = rotate(X, 20) + 5
plt.scatter(X2[:, 0], X2[:, 1], **colorize)
plt.axis('equal')
这说明 x 和 y 的值并不是数据间关系的必要基础特征。这个例子中真正的基础特征是每个点与数据集中其他点的距离。表示这种关系的常用方法是关系(距离)矩阵:对于 N 个点,构建一个 N × N 的矩阵,元素(i,j)是点 i 和点 j 之间的距离。我们用 Scikit-Learn 中的 pairwise_distances 函数来计算原始数据的关系矩阵:
from sklearn.metrics import pairwise_distances
D = pairwise_distances(X)
print(D.shape) # (1000, 1000)
正如前面所说的,对于 N = 1000 个点,获得了一个 1000 × 1000 的矩阵。画出该矩阵,如下图:
plt.imshow(D, zorder=2, cmap='Blues', interpolation='nearest')
plt.colorbar()
如果用类似方法为已经做过旋转和平移变换的数据构建一个距离矩阵,将看到同样的结果:
D2 = pairwise_distances(X2)
print(np.allclose(D, D2)) # True
这个距离矩阵给出了一个数据集内部关系的变现形式,这种形式与数据集的旋转和投影无关。但距离矩阵的可视化效果却显得不够直观。
虽然从(x,y)坐标计算这个距离矩阵很简单,但是从距离矩阵转换回 x 坐标值和 y 坐标值却非常困难。这就是多维标度法可以解决的问题:它可以将一个数据集的距离矩阵还原成一个 D 维坐标来表示数据集。下面来看看多维标度法是如何还原距离矩阵的——MDS 模型将非相似性参数设置为 precomputed 来处理距离矩阵:
from sklearn.manifold import MDS
model = MDS(n_components=2, dissimilarity='precomputed', random_state=1)
out = model.fit_transform(D)
plt.scatter(out[:, 0], out[:, 1], **colorize)
plt.axis('equal')
仅仅依靠描述数据点间关系的 N × N 距离矩阵,MDS 算法就可以为数据还原出一种可行的二维坐标。
6.3、将 MDS 用于流行学习
既然距离矩阵可以从数据的任意维度进行计算,那么这种方法绝对非常实用。既然可以在一个二维平面中简单地旋转数据,那么也可以用以下函数将其投影到三维空间(特别是前面介绍过的三维旋转矩阵):
def random_projection(X, dimension=3, rseed=42):
assert dimension >= X.shape[1]
rng = np.random.RandomState(rseed)
C = rng.randn(dimension, dimension)
e, V = np.linalg.eigh(np.dot(C, C.T))
return np.dot(X, V[:X.shape[1]])
X3 = random_projection(X, 3)
print(X3.shape) # (1000, 3)
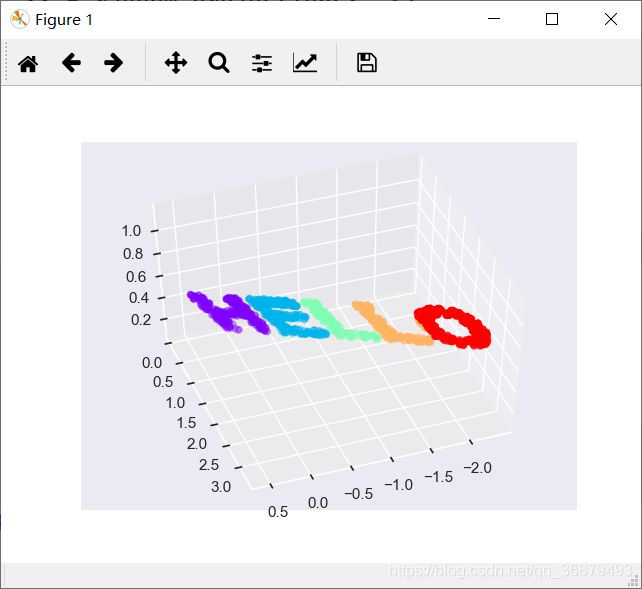
将这些点画出来,看看可视化效果:
from mpl_toolkits import mplot3d
ax = plt.axes(projection='3d')
ax.scatter(X3[:, 0], X3[:, 1], X3[:, 2],
**colorize)
ax.view_init(azim=70, elev=50)
现在可以通过 MDS 评估器输入这个三维数据,计算距离矩阵,然后得出距离矩阵的最优二维嵌入结果。结果还原了原始数据的形状:
from sklearn.manifold import MDS
model = MDS(n_components=2, random_state=1)
out3 = model.fit_transform(X3)
plt.scatter(out3[:, 0], out3[:, 1], **colorize)
plt.axis('equal')
以上就是使用流形学习评估器希望达成的基本目的:给定一个高维嵌入数据,寻找数据的一个低维表示,并保留数据间的特定关系。在 MDS 的示例中,保留的数据是每对数据点之间的距离。
6.4、非线性嵌入:当 MDS 失败时
前面介绍了线性嵌入模型,它包括将数据旋转、平移和缩放到一个高维空间的操作。但是当嵌入为非线性时,即超越简单的操作集合时,MDS 算法就会失效。现在来看看下面这个将输入数据在三维空间中扭曲成 “S” 形状的示例:
def make_hello_s_curve(X):
t = (X[:, 0] - 2) * 0.75 * np.pi
x = np.sin(t)
y = X[:, 1]
z = np.sign(t) * (np.cos(t) - 1)
return np.vstack((x, y, z)).T
XS = make_hello_s_curve(X)
from mpl_toolkits import mplot3d
ax = plt.axes(projection='3d')
ax.scatter(XS[:, 0], XS[:, 1], XS[:, 2],
**colorize)
虽然数据点间的基本关系仍然存在,但是这次数据以非线性的方式进行了变换:它被包裹成了 “S” 形。
如果尝试用一个简单的 MDS 算法来处理这个数据,就无法展示数据非线性嵌入的特征,进而导致我们丢失了这个嵌入式流形的内部基本关系特性:
from sklearn.manifold import MDS
model = MDS(n_components=2, random_state=2)
outS = model.fit_transform(XS)
plt.scatter(outS[:, 0], outS[:, 1], **colorize)
plt.axis('equal')
无法还原其内部结构。
6.5、非线性流形:局部线性嵌入
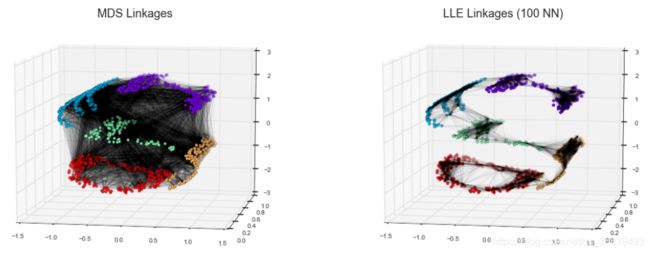
那么如何改进呢?在学习新的内容之前,先来回顾一下问题的源头:MDS 算法构建嵌入时,总是期望保留相距很远的数据点之间的距离。但是如果修改算法,让它只保留比较接近的点之间的距离呢?嵌入的结果可能会与我们的期望更接近。
我们可以将这两种思路想象成下图所示的情况:
from sklearn.manifold import LocallyLinearEmbedding
model = LocallyLinearEmbedding(n_neighbors=100, n_components=2,method='modified',
eigen_solver='dense')
out = model.fit_transform(XS)
fig, ax = plt.subplots()
ax.scatter(out[:, 0], out[:, 1], **colorize)
ax.set_ylim(0.15, -0.15)