递归算法总结

概念

递归算法是一种从上到下的算法，简单理解：不停直接或间接调用自身函数，每次调用会改变一个或者多个变量，直到变量到达边界，结束调用。

借用知乎上Memoria的回答：

假设你在一个电影院，你想知道自己坐在哪一排，但是前面人很多，你懒得去数了，于是你问前一排的人「你坐在哪一排？」，这样前面的人 (代号 A) 回答你以后，你就知道自己在哪一排了——只要把 A 的答案加一，就是自己所在的排了。不料 A 比你还懒，他也不想数，于是他也问他前面的人 B「你坐在哪一排？」，这样 A 可以用和你一模一样的步骤知道自己所在的排。然后 B 也如法炮制。直到他们这一串人问到了最前面的一排，第一排的人告诉问问题的人「我在第一排」。最后大家就都知道自己在哪一排了。

递归的核心思想是分治策略，也就是将一个规模大的问题分解成一些规模小的同类问题，然后通过这些小问题求得大问题的解。

递归算法和分治法的区别：递归是算法的实现方式，分治是算法的设计思想。 这跟你吃饭可以用筷子吃，也用手吃一样。也就是我使用的是分治法的思想，但不一定使用递归算法来实现该实现。

递归：先递，也就是从上到下计算，然后再归，也就是从下到上返回结果。

递归算法的设计

1. 函数的功能。
2. 递归部分（递推公式）：题目有可能直接给出公式，不然只能自己推出来，利用将大问题不断分成小问题。
3. 找出递归的终止条件：比如上面电影院例子，当第一排时就结束，并返回一个结果。一般结合递推公式。

递归算法的优缺点

递归算法的时间复杂度是O(n^2)，所以也是比较暴力破解算法。

优点：只需要几条代码就可以解决问题。

缺点：

1. 有时因为太过简洁而难理解过程。
2. 递归会保存大量临时数据和重复的数据，太多的话，会造成栈溢出，程序崩溃。
3. 数据规模大时，运行时间可能会超时。

经典例题

1.、求解Fibonacci数列的第n个位置的值？（斐波纳契数列（Fibonacci Sequence），又称黄金分割数列，指的是这样一个数列：1、1、2、3、5、8、13、21、
……在数学上，斐波纳契数列以如下被以递归的方法定义：F1=1,F2=1,Fn=F（n-1）+F（n-2）（n>2,n∈N*））。

设计步骤：

1.函数功能：设计f(n)表示的是返回第n个位置的值。
2.递归部分：Fn=F（n-1）+F（n-2）（n>2,n∈N*）），也就是一个数会等于前两个数相加的结果。
3.找出终止条件：当n=1时，F1=1；当n=2时，F2=1。

代码：

public class Fibonacci {
    public static int fib(int n){
        // 1. 终止条件
        if(n == 1 || n == 2){
            // 2.终止完要返回什么
            return 1;
        }
        // 3.递归部分
        return fib(n-1) + fib(n-2);
    }
    public static void main(String[] args) {
        System.out.println(fib(10));
    }
}

可以试试你的n很大的话(n=100即可感受到)，这段代码会运行半天还没算出结果，这就是递归算法的缺点。用动态规划也可以做而且更好更快计算，不过现在这里是学递归算法。后面到动态规划会拿出来优化。

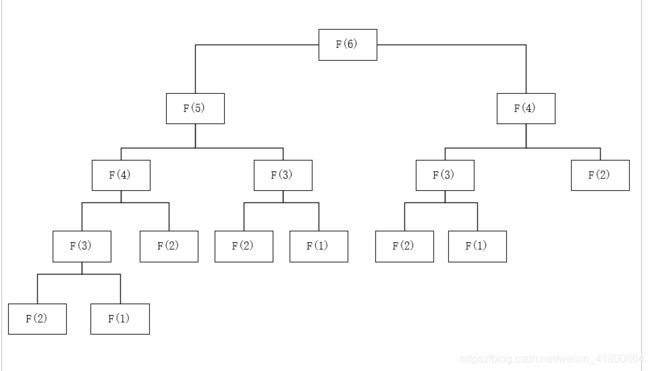
过程图：

如图可以看到，像F(4)和F(3)重复计算了几次，也就导致要多些运算时间和内存空间。

2、 假设你正在爬楼梯。需要n阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

这道题跟上面的题类似，但是没直接给公式，需要推导。

函数的设计：设计f(n)表示求出有多少种不同方法爬到n阶到楼顶。

求递推公式：每次你可以爬 1 或 2 个台阶，利用从上到下的思想，那么对于爬到第n阶可能是由第n-1阶爬上来，也可能是从第n-2阶爬上来。那么有多少种方法爬到第n阶可以变成 有多少种方法爬到第n-1阶 加上 有多少种方法爬到第n-2阶 的和。即递推公式为：f(n)=f(n-1)+f(n-2)。

终止条件：当我在第1阶时返回1，还有第2阶时返回2。必须要有第2阶的初始值，因为如果f(2)的话，公式为f(2)=f(1)+(0)，那f(0)又会递归调用，得f(0)=f(-1)+f(-2)，就造成死循环，当然，也可以加上f(0)的初始值。

public int climbStairs(int n) {
     
    if(n <= 2){
     
        return n;
    }
    return climbStairs(n-1)+climbStairs(n-2);
}

如果在leetcode上直接提交会超时，因为重复计算太多了。最下面再说优化。

3、 阶乘

1. 函数功能：设计f(n)表示求第n阶的阶乘数。
2. 递归部分：阶乘的原公式是：n!=n*(n-1)*(n-2)...3\*2\*1，根据将大问题分解成小问题，我们把它转换成这样：n!=n\*f(n-1)!。
3. 终止条件就是当n=1时返回1。

核心代码：

public static int factorial(int n){
     
    if(n == 1){
     
        return 1;
    }
    return n*factorial(n-1);
}

过程图：

4、 汉诺塔问题是一个经典的递归问题。汉诺塔（Hanoi Tower），又称河内塔，源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，
在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。假设我们需要这些盘片从A柱移动到C柱，应该如何操作？

解决：
主要是利用汉诺塔理解下递归的思想。

来分析它的步骤：（->表示移动）

现在假设只有一个盘片，那么直接就是：A->C

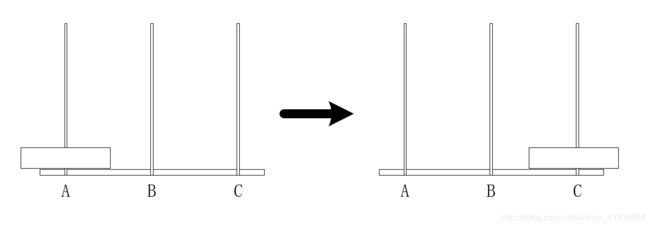
假设现在有两个盘片，那么就需要三步：

1. 从A柱最顶的盘片移动到B柱：A->B
2. 然后A柱现在只剩最底的盘片，也是最大的盘片，移动到C柱：A->C
3. 最后B柱上的盘片移动到C：B->C

对于此三步，我们再解析一下：

• 当第一步A->B完成后，其实问题就变回了当在A柱上只有一个盘片时怎么操作的问题，因为此时A柱就剩最底的一个盘片啊，所以跟上面只有一个盘片的解决方式一样，直接A->C。
• 那么第三步呢？第三步其实也是跟只有一个盘片的解决方式一样，只不过现在是在B柱，那么你可以看成，是B->A->C，也就是把B柱的盘片先移动到A柱，然后再从A柱移动到C柱，这样对结果并没有影响并且只是做个思想转换，而且当从A柱移动到C柱，又回到了只有一个盘片的解决方式一样。
  

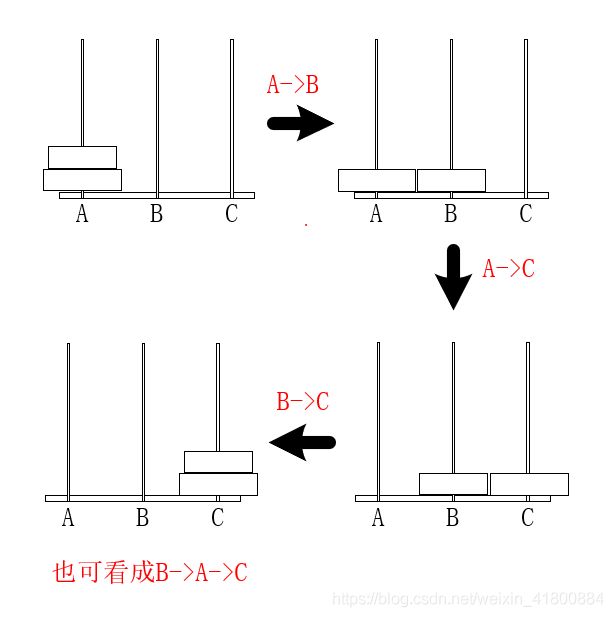
当有三个盘片时，我们把三个盘片从上到下编号1，2，3。想要让A柱编号3的盘片移动到C柱，必须先移开A柱前两个盘片，然后才可以把A柱编号3的盘片移动到C柱。我们可以直接把前两个当成一个整体直接移动到B柱，不在意怎么移的，然后把编号3的盘片移动到C柱。如图：

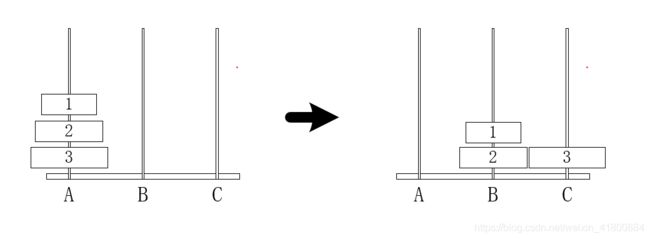
通过这张图可得，目前我们已经解决了移动编号3的盘片的问题，那么剩下的问题就是解决在B柱上的两个盘片该如何操作？这不就是转变成只有两个盘片时该如何移动的问题了吗？虽然现在是在B柱上，那么这跟刚刚有两个盘片的操作一样。

后面四个盘片五个盘片…n个盘片都是一样的递归思想，至此对于汉诺塔的递归思想应该是有头绪了。

总结：
对于有n个盘片的汉诺塔，我们把n-1个盘片当成一个整体移动到B柱（不用去管细节，怎么移动的，反正移到最后一步肯定是这样的结果，但是得知道，肯定是借助C柱来把这些盘片从A柱移动到B柱，也就是会将其中的柱作为辅助柱来辅助移动，这句等下可以理解代码），然后把第n个盘片移动到C柱，最后继续解决n-1个盘片如何移动的问题。一直到n=1时，直接A->C。

因为解决F(N)之前解决F(N-1),而解决F(N-1)之前解决F(N-2)，直到n=1，所以递归时首先打印的就是n=1时的移动，然后一直一直回退打印，直到最后打印F(N)。跟前两道的例题运行流程图一样。

代码实现：

public class HanoiTower {
    /**
     *
     * @param n 盘片数
     * @param a 柱子A
     * @param b 柱子B
     * @param c 柱子C
     * @return 移动步骤
     */
    public static void hanoi(int n, char a, char b, char c){
        // 终止条件
        if(n == 1){
            // 剩最后一个盘片时直接从A移动到C
            System.out.println(a + "->" + c);
        } else {
            // 第一步，把n-1当成整体，从A移动到B，以C柱作为辅助柱来辅助移动，但我们只需要移动后的结果。
            hanoi(n-1, a, c, b);
            // 第二步，剩最后一个盘片时直接从A移动到C
            System.out.println(a + "->" + c);
            // 第三步，继续解决n-1的问题，此时的问题变成在B柱移动到C柱如何操作
            // 从B移动到C，以A柱作为辅助柱
            hanoi(n-1, b, a, c);
        }
    }

    public static void main(String[] args) {
        hanoi(3,'A','B','C');
    }

}

当n=3时，它的运行结果是：

A->C
A->B
C->B
A->C
B->A
B->C
A->C

会疑惑，第一步是A->C???而不是A->B???
正如前面所说，递归是解决F(N)之前解决F(N-1),而解决F(N-1)之前解决F(N-2)，并且我们是将前两片当成一个整体的思路移动到B柱，实际上是：编号1的盘片先从A移动到C，然后编号2的盘片从A移动到B，最后编号1的盘片从C移动到B。

所以在设计递归算法时是不需要去在意细节，我们把F(N-1)当作一个整体，去解决F(N)。

递归算法的优化

通过前面的例题和图片，可以发现到递归算法在计算过程中出现许多重复的计算，这就是导致时间复杂度高的地方。所以根据该缺点，我们可以做出优化：保存计算结果，当遇到要重复计算时直接拿出结果：在Java中可以使用Map或者数组来解决。

当然有些就不一定要使用Map或数组来保存计算结果，比如斐波那契数列的优化，可以使用从下到上的思想，借助一个临时数据来保存一个结果就够了：

public int climbStairs(int n) {
    if(n <= 2){
        return n;
    }
    int j = 1;
    int o = 2;
    // 利用一个临时变量
    int temp = 0;
    for(int i = 3; i <= n; i++){
        temp = j + o;
        // 交换
        j = o;
        o = temp;
    }
    return o;
}

参考：
乌枭的递归整理
汉诺塔