ACM Weekly 5(待修改)

涉及的知识点

第五周练习主要涉及string类、Kmp、manacher、字符串hash

拓展：BM、Sunday、

string类

string是C++相对于C特有的类型，将字符串单独封装作为类使用，其基本的操作不再赘述。

以下内容参考《C++STL基础及应用》

基本操作

插入

insert()：第一个参数表明插入源串的位置，第二个参数表明要插入的字符串；
append()：仅有一个输入参数，在源字符串尾部追加该字符串
size()：无参数，返回字符串长度值，即多少个字符

替换

replace()：三个输入参数，第一个用于指示从字符串什么位置开始改写，第二个用于指示从原字符串中删除多少个字符，第三个是替换字符串的值

查询

string::npos：string类的成员变量，一般与系统查询函数的返回值比较，若等于该值，表明没有符合查询条件的结果值

find：在一个字符串中查找指定的单个字符或字符组，找到返回首次匹配的开始位置，否则返回nops，一般为两参数，待查询字符串和起始位置（默认0）

find_first_of：在一个字符串中进行查找，返回第一个与指定字符串中任何字符匹配的字符位置，否则为npos，一般为两参数，待查询字符串和起始位置（默认0）

find_last_of：在一个字符串中进行查找，返回最后一个与指定字符串中任何字符匹配的字符位置，否则为npos，一般为两参数，待查询字符串和起始位置（默认0）

find_first_not_of：在一个字符串中进行查找，返回第一个与指定字符串中任何字符不匹配的字符位置，否则为npos，一般为两参数，待查询字符串和起始位置（默认0）

find_last_not_of：在一个字符串中进行查找，返回最后一个与指定字符串中任何字符不匹配的字符位置，否则为npos，一般为两参数，待查询字符串和起始位置（默认0）

rfind：对一个串从头到尾查找指定的单个字符或字符组，如果找到，返回首次匹配开始位置，否则返回npos，一般为两参数，待查询字符串和起始位置（默认串尾）

字符串输入输出流

头文件<sstream>

istringstream：字符串输入流，提供读string功能
ostringstream：字符串输出流，提供写string功能
stringstream：字符串输入输出流，提供读写string功能

此三类配合>>和<<使用，方向代表存入的对象

KMP

KMP原理

KMP算法应用于查找B串在A串中的出现位置，也可以通过修改来求得两个字符串的最大公共序列，初次理解总觉晦涩难懂，查找多方资料并细细品读后才得以理解，本文尽力将KMP算法论述清楚

参考了该篇博客，其详尽自愧不如

还有mooc上的网课数据结构-浙江大学

匹配机理

每次匹配，正在匹配的模式串的部分分为三个板块

该处对称的定义：最大的相同前缀与后缀

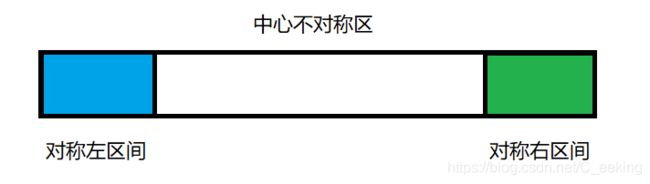
正常来讲是这样，但是为了简化操作，只取前三块

匹配如图（前提：匹配失败）

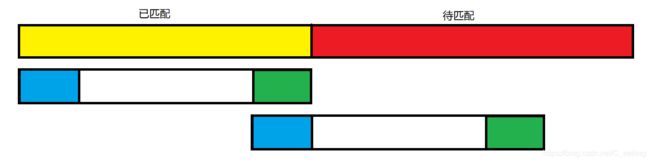
首先是直观的理解，在KMP中，每次失配后，串移动的参照物为文本串，也就是每次都是移动模式串，即更改模式串的匹配位置，由图可知，每次失配后，为了减少再次匹配的次数，我们由对称进行移动，将左对称区间移动到右区间位置，中间的元素必定不能匹配，由上一张图可知，模式串中已匹配部分有三个板块，若按照暴力的思想右移一位，如图

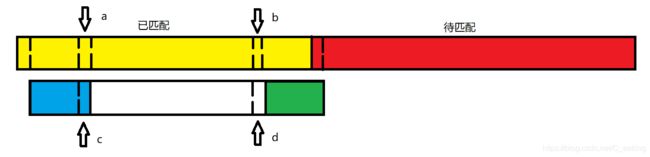
可以看到，右移之后a与c匹配判断，b与d匹配判断，看下面的例子

$AACDAAF$
$AACDAA$
→
$AACDAAF$
$\ast AACDAA$
如果需要对称部分匹配成功，则C=A，D=A，模式串变为AAAAAA，显然与设定的条件矛盾

如果没有对称区间，那么就直接右移一位
设两个区间左端相隔m位

易证，右移一位，则串各元素全相等，右移两位，则奇数相等，偶数相等，由不完全归纳可得右移m位，则以m为模的对应位数元素相等

那么，接下来的问题就是如何进行移动操作，以及求对称长度的大小

next/match数组的构建

如图

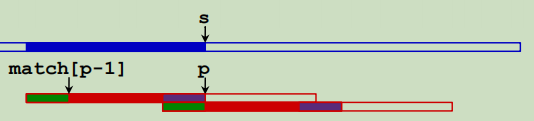
当s与p指向的元素相同时，两者都自增，当发生匹配失败时，p=match[p-1]+1，进行回溯，即将左对称移到右对称，或者说重新从左对称的最大下标的下一个开始匹配，这里的match的定义是

简单来说，match记录的是当模式串到下标j（是下标，也就是j+1个元素）时，满足下标0~j的字符串中有最大相等的前缀后缀的下标i

那么，在match已经构造好的前提下，代码如下

int KMP(char*text,char*pattern)
{
     
	int n = strlen(string);
	int m = strlen(pattern);
	int s=0, p=0;
	if ( n < m ) return -1;
	while ( s<n && p<m ) {
     
		if ( text[s]==pattern[p] ) 
		{
     
			s++; 
			p++;
		}
		else if(p>0)//p=0代表第一个元素不匹配 
			p = match[p-1]+1;
		else s++;//第一个元素不匹配，则进行text的下一位匹配
	}
	return ( p==m )? (s-m) : -1;//判断p是否到达结尾，是，则说明已经找到，否则说明匹配失败
}

现在来讨论一下match的构造

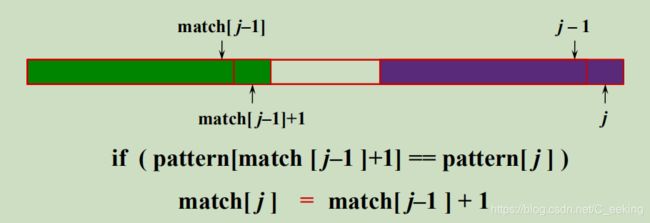
我们用递归的方式来思考，对j-1来言，与其相等的字符下标为match[j-1]，当我们讨论j的值时，有两种情况

1. pattern[j]的存在能使pattern的最大相同前缀与后缀值增加
   由图可知，绿色部分到match[j-1]与紫色部分到j-1两部分相等，如果pattern[j]与pattern[match[j-1]+1]相等，那么相同前缀后缀的长度便可以增加，增加的长度为1

2. pattern[j]的存在不能使pattern的最大相同前缀与后缀值增加
   此时就要思考如何利用先前的结果了，此时已经知道pattern[match[j-1]+1]≠pattern[j]，如图，但是由于对称，绿1部分等于紫2部分，之后便又回到了上一点的判断，即判断pattern[match[match[j-1]]]是否等于pattern[j]，若不相等，则循环，如果到最后仍不相等，match[j]=-1

代码如下

void BuildMatch(char*pattern)
{
     
	memset(match,0,sizeof(match));//清空
	int i=0,len=strlen(pattern);//数值初始化
	match[0]=-1;//第一个为-1
	for(int j=1;j<=m;j++)//求每一个的match值
	{
     
		i=match[j-1];
		while(i>=0&&pattern[i]!=pattern[j])//递归过程，找到第一个前缀的后一个元素与pattern[j]相等
			i=match[i];//减小长度，有DP的意思
		if(i<0)
			match[j]=-1;//如果找不到
		else
			match[j]=match[j-1]+1;
	}
}

拓展KMP

Manacher

字符串哈希

字符串哈希可以简单理解为将字符串对应成整数来处理，用函数的思想（数学中的函数）将每个字符串对应到存储空间的各个位置上，即通过哈希函数尽量创造出一个一一对应的数组，方便进行后续操作

哈希方法

对于给定的字符串str，由字母组成，设置一个字母T对应映射$idx(T)=T{-}^{\prime }{a}^{\prime }+1(idx(T)=(int)T)$

自然溢出

$hash[i]=hash[i-1]\times p+id(str[i])$
hash[i]设置为unsighed long long，相当于默认对$2^{64}-1$取模

单哈希

$hash[i]=hash[i-1]\times p+id(str[i])\%mod$
其中p、mod为质数，mod>p，当mod、p很大时，冲突概率低

双哈希

将一个字符用不同mod进行两次哈希，哈希结果为一个二元组
$has{h}_1[i]=hash[i-1]\times p+id(str[i])\%mo{d}_1$
$has{h}_2[i]=hash[i-1]\times p+id(str[i])\%mo{d}_2$
结果为$<has{h}_1[n],has{h}_2[n]>$
由于进行了两次哈希，并且用的mod不同，冲突概率极低

获取子串哈希

已知一个字符串str的$hash[i],1\le i\le n$，其子串$st{r}_l\dots st{r}_r(1\le l\le r\le n)$的哈希值为
$hash[r]-hash[l-1]\times p^{r-l+1}$
又因为需要每次取模
$(hash[r]-hash[l-1]\times p^{r-l+1})\%mod$
再加上考虑负数的情况

难题解析

拓展

参考文献

1. 从头到尾彻底理解KMP
2. 本文部分图与代码来自数据结构 浙江大学 中国大学MOOC（慕课）
3. 《C++STL基础及应用》