ACM Weekly 6（待修改）

前言

学习ACM的知识已经到了第6周，之前所涉及的知识点还有许多地方需要裨补阙漏，还有几篇博客的材料计划后期重新将所有知识点与队里给出的题进行深化与再训练，学业繁忙，可能要到寒假才能实现，在此给自己以警示。

涉及的知识点

第六周的练习主要涉及树和图的存储、最短路迪杰斯特拉算法和其优化、最小生成树算法、并查集原理以及应用
拓展：LCA最近公共祖先、堆及其实现、Floyd-Warshall、Bellman-Ford、SPFA、基环树、负环判断、差分约束、树的直径

树与图的存储

树

根据老师的授课内容与数据结构方面的相关书籍，总结出树常用的存储方式有以下几种

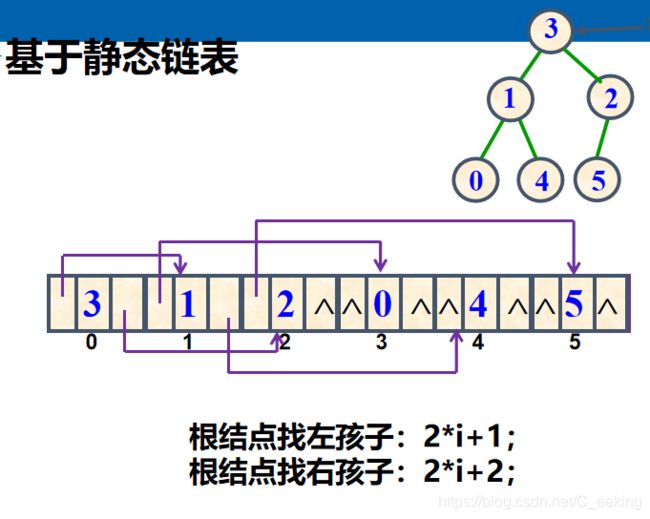
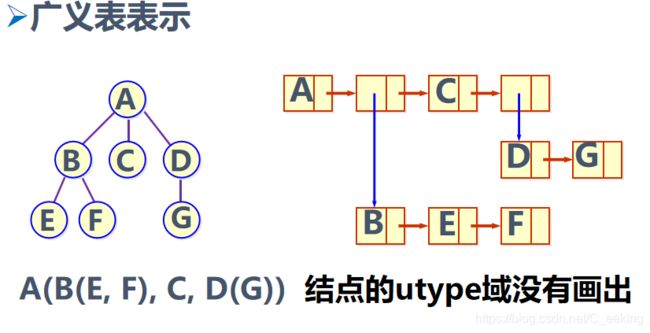
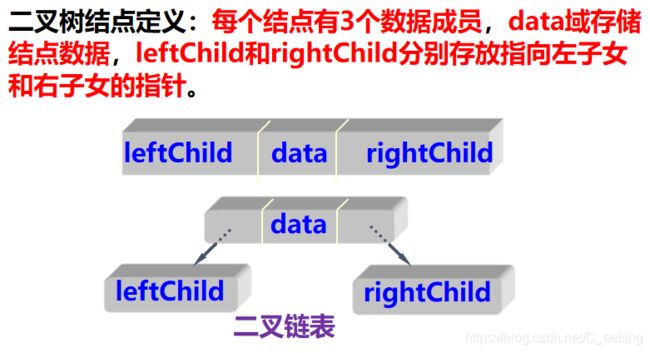
1. 静态链表（针对二叉树）

template<typename T>
struct TreeNode
{
     
      T data;
      TreeNode<T>*  lchild;
      TreeNode<T>*  rchild;
};
template<typename T>
struct TreeNode
{
     
      T data;
      int  lchild;
      int  rchild;
};

效果如图

2. 数组（针对二叉树）
   对于元素i(以0开始存储)，其左子树下标为2×i+1，右子树下标为2×i+2，一般用于完全二叉树、满二叉树
   效果如图
   

3. 广义表
   效果如图
   

4. 兄弟/二叉链表（非静态链表）

struct TreeNode
{
     
     T data;
     TreeNode<T>*  lchild;
     TreeNode<T>* rchild;
     TreeNode(TreeNode<T>* lc=NULL, TreeNode<T>* rc=NULL)
     {
     
           lchild=lc;
           rchild=rc;
     }
     TreeNode(const T& elem, TreeNode<T>* lc=NULL, TreeNode<T>* rc=NULL)
     {
     
           data=elem;
           lchild=lc;
           rchild=rc;
     }
};

效果如图

题目

图

根据课堂内容以及自己理解，总结出图所常用的存储结构，因为实现起来较易，所以不额外给出代码

1. 邻接矩阵
   如图
   

2. 邻接链表
   如图
   

Dijkstra算法

基本使用

Dijkstra算法是解决单源最短路径的常用办法，不过只适用于边的权重为正的情况，但是其拓展性较强，可以适应许多问题，并且与堆结合可以拥有更快的效率。

算法思想：每次找到距源点最短的顶点，以该顶点为中心进行拓展，最终得到源点到其余各点的最短路径。

基本步骤：

1、将所有顶点分为两部分：已知最短路径的顶点集合A和未知最短路径的B
2、设置源点到自己的最短路径长度为0，将源点的邻接点的最短路径设为与源点边的权重，其他点最短路径设置为正无穷
3、在B中所有顶点中选择一个离源点最近的顶点u加入到A中，并考察所有以点u为起点的边，对每一条边进行松弛操作，例如存在一条从u到v的边，那么可以将u->v添加到尾部来拓展从源点到v的路径，路径长度是dis[u]+Graph[u][v]，如果这个值比dis[v]小，用dis[u]+Graph[u][v]来代替
4、重复第3步直到B为空

代码实现

#include 
#define INF 99999
using namespace std;
bool visited[1212];//判断是否已经访问过
int Graph[1212][1212],Dis[1212],Start,End,N,M;
//Graph存储权重，Dis存储各点到源点的最小距离
//Start、End为起点终点，N为顶点数，M为边数
void Dijkstra()
{
     
    int m=INF,loc;
    for(int i=1; i<=N; i++)
        if(Dis[i]<m&&!visited[i])//找出离源点最近的未收录的顶点
        {
     
            m=Dis[i];
            loc=i;
        }
    visited[loc]=true;//收录
    for(int i=1; i<=N; i++)
        if(Graph[loc][i]<INF&&Dis[loc]+Graph[loc][i]<Dis[i])
        //进行松弛操作，判断这个已收录的顶点能否使其领接点到源点的距离变小
            Dis[i]=Dis[loc]+Graph[loc][i];
}
int main()
{
     
    freopen("test.txt","r",stdin);
    cin >>N>>M>>Start>>End;
    for(int i=1; i<=N; i++)
        for(int j=1; j<=N; j++)
            if(i!=j)
                Graph[i][j]=INF;//初始化
    while(M--)
    {
     
        int a,b,w;
        cin >>a>>b>>w;
        Graph[a][b]=w;//Dijkstra处理有向图
    }
    for(int i=1; i<=N; i++)
        Dis[i]=Graph[Start][i];//路径初始化
    visited[Start]=true;
    for(int i=1; i<N; i++)//每次收录一个顶点并以它为中心进行松弛
        Dijkstra();
    for(int i=1; i<=N; i++)
        cout <<Dis[i]<<" ";
    return 0;
}

优化

仔细分析可以发现，先前给出的代码其实可以进行优化，首先，使用邻接表来存储可以减少大量不必要的查找和空间开销

其次，如果采用堆/优先队列的数据结构来存储各点的最短路径，也可以简化不必要的查找

思想如图

代码优化

#include 
#include 
#include 
#include 
#include 
#define INF 99999
using namespace std;
bool visited[1212];//判断是否已经访问过
typedef struct PR
{
     
    int first,second;
    PR(int _id,int _w)
    {
     
        first=_id;
        second=_w;
    }
    bool operator>(const PR&b)const
    {
     
        return this->second>b.second;
    }
}PR;//设置变量，第一个是编号，第二个是权重
vector<PR>Graph[1212];//用vector来模拟链表
priority_queue<PR,vector<PR>,greater<PR> >Heap;//优先队列，堆
int Dis[1212];
int Start,End,N,M;
//Graph存储点的编号以及对应的权重，Dis存储各点到源点的最小距离
//Start、End为起点终点，N为顶点数，M为边数
void Dijkstra()
{
     
    while(!Heap.empty())
    {
     
        PR t=Heap.top();//离源点最近的点
        Heap.pop();
        if(visited[t.first])
            continue;
        visited[t.first]=true;
        for(unsigned int i=0;i<Graph[t.first].size();i++)//每次收录一个顶点并以它为中心进行松弛
            if(Graph[t.first][i].second<INF&&Dis[Graph[t.first][i].first]>Dis[t.first]+Graph[t.first][i].second)
            {
     
                Dis[Graph[t.first][i].first]=Dis[t.first]+Graph[t.first][i].second;
                Heap.push(PR(Graph[t.first][i].first,Dis[Graph[t.first][i].first]));
            }
            /*
            基本思想与先前的代码相同，在这里解释一下所写代码变量的含义
            Graph[t.first]:离源点最近点t的所有邻接点
            Graph[t.first][i].first:t的第i+1个邻接点的编号
            Graph[t.first][i].second:t的第i+1个邻接点与t的距离
            Dis[Graph[t.first][i].first]:t的第i+1个邻接点到源点的距离
            */
    }
}
int main()
{
     
    freopen("test.txt","r",stdin);
    cin >>N>>M>>Start>>End;
    while(M--)
    {
     
        int a,b,w;
        cin >>a>>b>>w;
        Graph[a].push_back(PR(b,w));//Dijkstra处理有向图
    }
    for(int i=1;i<=N;i++)
        Dis[i]=INF;
    for(unsigned int i=0;i<Graph[Start].size();i++)
        Dis[Graph[Start][i].first]=Graph[Start][i].second;
    Dis[Start]=0;
    for(int i=1;i<=N;i++)
        Heap.push(PR(i,Dis[i]));
        Dijkstra();
    for(int i=1; i<=N; i++)
        cout <<Dis[i]<<" ";
    return 0;
}

并查集

并查集基础

在并查集里，占有重要地位的便是对父节点的存储与路径压缩算法，在没有使用并查集进行合并之前，图上的点都是散乱的，或单独节点，或是成为一棵树，并不是连通的，并查集通过查找点之间的关系进行合并，最终使各节点合成了几棵逻辑清晰的树，整体为森林

具体理论实现请参考参考文献中的文章链接关于并查集的部分

代码

int Seek(int& x)//寻找源头
{
     
    if(Origin[x]==x)
        return x;
    else return Origin[x]=Seek(Origin[x]);//路径优化
}
bool Union(int&x,int&y)//判断是否已经在一个集合中
{
     
    int Ori_x=Seek(x),Ori_y=Seek(y);
    if(Ori_x!=Ori_y)//如果源头不等，说明不在一个集合中，所以需要合并
    {
     
        Origin[Ori_y]=Ori_x;
        return true;
    }
    return false;
}

进阶

并查集的进阶算法主要针对带权并查集，在上面的代码中，并查集中节点所涉及到的关系只有两种，即是否为祖先，而带权并查集所涉及的关系有多种，例如一个关系循环链：A->B、B->C、C->A，那么对每次输入的两个元素进行关系判断就不能用单纯的是否为祖先来判断了。

最小生成树算法

最小生成树在图中有着广泛的运用，总结起来就是在连通图中找到总共N个节点的N-1条边，边的总权重和最小，且这些边能生成一棵树将所有节点相连

Prim

Prim算法和Dijkstra算法在许多地方有类似之处，Prim算法是存储各顶点到已经生成的最小生成树的“树距”，Dijkstra算法是存储各顶点到源点的“点距”

算法思想：将顶点分为已入树顶点与未入树顶点，首先选择任意一个顶点加入生成树，之后找到在每一个树顶点到每一个非树顶点的边中找到最短边加入生成树，执行n-1次（通过枚举）

基本步骤：

1、从任意一个顶点开始构造生成树，设从一号顶点，将一号顶点加入生成树
2、最初生成树只有1号节点，初始化距离数组Dis
3、从Dis中选出离生成树最近的顶点j加入生成树中，以该点为中间点，更新生成树到每一个非树顶点的距离，即Dis[k]>e[j][k]时Dis[k]=e[j][k]
4、重复3，直到n个顶点都入树

代码实现

此代码直接使用领接表+堆来进行优化

#include 
#include 
#include 
#include 
#include 
#define INF 99999
using namespace std;
typedef struct PR
{
     
    int first,second;
    PR(int _id,int _w)
    {
     
        first=_id;
        second=_w;
    }
    bool operator>(const PR&b)const
    {
     
        return this->second>b.second;
    }
}PR;
priority_queue<PR,vector<PR>,greater<PR>>Heap;
int Dis[1212],ans,N,M;
bool visited[1212];
vector<PR>Graph[1212];
void Prim()
{
     
    int acc=0;
    Heap.push(PR(1,Dis[1]));
    while(!Heap.empty()&&acc!=N-1)
    {
     
        PR t=Heap.top();
        Heap.pop();
        if(visited[t.first])
            continue;
        visited[t.first]=true;
        ans+=t.second;
        for(unsigned int i=0; i<Graph[t.first].size(); i++)
            if(Dis[Graph[t.first][i].first]>Graph[t.first][i].second)//如果树距能被松弛
            {
     
                Dis[Graph[t.first][i].first]=Graph[t.first][i].second;
                Heap.push(PR(Graph[t.first][i].first,Dis[Graph[t.first][i].first]));
            }
    }
}
int main()
{
     
    freopen("test.txt","r",stdin);
    cin >>N>>M;
    while(M--)
    {
     
        int s,e,w;
        cin>>s>>e>>w;
        Graph[s].push_back(PR(e,w));
        Graph[e].push_back(PR(s,w));
    }
    for(int i=1; i<=N; i++)
        Dis[i]=INF;
    for(unsigned int i=0; i<Graph[1].size(); i++)
        Dis[Graph[1][i].first]=Graph[1][i].second;
    Dis[1]=0;
    for(int i=1; i<=N; i++)
        Heap.push(PR(i,Dis[i]));
    Prim();
    cout <<ans;
    return 0;
}

Kruskal

Kruskal算法对于最小生成树的构造符合我们的常用认知，即从边的集合中找出最小值、次小值、次次小值等来构成所需要的树，但是在拿取边的时候需要判断是否会构成连通域，使用并查集来判断，理论上能用BFS和DFS，但是效率低

算法思想：每次选取未使用的最短边进行构建

基本步骤：

按照边的权值进行从小到大进行排序，每次从剩余边中选择权值较小且不会产生回路的边加入到生成树中，直到加了n-1条边

代码实现

#include 
#include 
#include 
#include 
#include 
using namespace std;
typedef struct Edge
{
     
    int s,e,w;
    Edge(int&_s,int&_e,int&_w)
    {
     
        s=_s;
        e=_e;
        w=_w;
    }
    bool operator<(const Edge& b)const//重载符号，便于使用优先队列，这里故意重载相反的符号，用于构造最小堆
    {
     
        return this->w>b.w;
    }
} Edge;
priority_queue<Edge>Heap;
int Origin[1212],N,M,ans;
int Seek(int& x)//寻找源头
{
     
    if(Origin[x]==x)
        return x;
    else return Origin[x]=Seek(Origin[x]);//路径优化
}
bool Union(int&x,int&y)//判断是否已经在一个集合中
{
     
    int Ori_x=Seek(x),Ori_y=Seek(y);
    if(Ori_x!=Ori_y)//如果源头不等，说明不再一个集合中，所以需要合并
    {
     
        Origin[Ori_y]=Ori_x;
        return true;
    }
    return false;//否则不能取这条边
}
void Kruskal()
{
     
    int acc=0;
    while(!Heap.empty()&&acc!=N-1)
    {
     
        Edge t=Heap.top();
        Heap.pop();
        if(Union(t.s,t.e))
        {
     
            acc++;
            ans+=t.w;
        }
    }
}
int main()
{
     
    freopen("test.txt","r",stdin);
    cin >>N>>M;
    for(int i=1; i<=N; i++)//初始化
        Origin[i]=i;
    for(int i=0; i<M; i++)
    {
     
        int s,e,w;
        cin >>s>>e>>w;
        Heap.push(Edge(s,e,w));//构造堆
    }
    Kruskal();
    cout <<ans;//输出最小生成树权重和
    return 0;
}

例题

题目大意：给出n个点间m条边的有向路径的长度、方向，找出从1走到n路径中路径长度最小值的最大值

思路：构造一个最小生成树，每次找出最大边，等到1和n加入树的时候，输出所记录的最小值

代码

#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
typedef struct Edge
{
     
    int s,e,w;
    Edge(int&_s,int&_e,int&_w)
    {
     
        s=_s;
        e=_e;
        w=_w;
    }
    bool operator<(const Edge& b)const
    {
     
        return this->w<b.w;
    }
} Edge;
priority_queue<Edge>Heap;
int Origin[1212],N,M,ans=1000001;
int Seek(int x)
{
     
    if(Origin[x]==x)
        return x;
    else return Origin[x]=Seek(Origin[x]);
}
bool Union(int&x,int&y)
{
     
    int Ori_x=Seek(x),Ori_y=Seek(y);
    if(Ori_x!=Ori_y)
    {
     
        Origin[Ori_y]=Ori_x;
        return true;
    }
    return false;
}
void Kruskal()
{
     
    while(!Heap.empty())
    {
     
        Edge t=Heap.top();
        Heap.pop();
        if(Union(t.s,t.e))
        {
     
            ans=min(t.w,ans);
            if(Seek(1)==Seek(N))
                break;
        }
    }
}
int main()
{
     
    int K;
    cin >>K;
    for(int i=1; i<=K; i++)
    {
     
        cin >>N>>M;
        for(int i=1; i<=N; i++)
            Origin[i]=i;
        for(int i=0; i<M; i++)
        {
     
            int s,e,w;
            cin >>s>>e>>w;
            Heap.push(Edge(s,e,w));
        }
        Kruskal();
        cout <<"Scenario #"<<i<<":"<<endl;
        cout <<ans<<endl<<endl;
        ans=1000001;
        while(!Heap.empty())
            Heap.pop();
    }
    return 0;
}

难题解析

拓展

LCA最近公共祖先

堆

Floyd-Warshall

Bellman-Ford

SPFA

基环树

负环判断

差分约束

树的直径

参考文献

1. 《啊哈算法》
2. 数据结构4–并查集入门
3. 并查集（进阶）