C语言授课记录（二）

导语

本次授课内容如下浅谈递归、快速排序、指针和数组、常用做题技巧、常见错误规避

有时间则讲解：递归的优化、递归与递推

辅助教材为《C语言程序设计现代方法》

浅谈递归

教材p144（左上）

递归是程序设计中常用的技巧，它能简化代码量，并且获得片面的较为清晰的逻辑，但是随之而来的是整体逻辑的复杂性与程序的低效（未优化前提下），工作栈被多次使用，程序包含了大量重复的计算使得其效率低下。

教材上的讲解采用了最简单的几个例子，如阶乘的运算、幂函数的运算，这里给出几个不同的例子，理解起来比教材上的更复杂一些，但难度并不大。

例题1

给定一个整数序列，要求程序使用递归来求出该序列的和。

思路

题目要求使用递归来求和，经过思考我们可以得知，程序可以通过递归模拟一般的顺序累和或者先进行二分，再进行区间累和。

代码

#include 
#include 
int N,data[100],i;
int sum(int l,int r)
{
     
    if(l<r)
    {
     
//        printf("%d",sum(l,(l+r)/2));
//        printf("%d\n",sum((l+r)/2+1,r));
        return sum(l,(l+r)/2)+sum((l+r)/2+1,r);//思考一下为什么这里要+1，+1可以去掉吗？
//        return sum(l,(l+r)>>1)+sum(((l+r)>>1)+1,r);//位运算优化
    }
    else if(l==r)
        return data[l];
    return 0;
}
int sum_(int n)
{
     
    if(n==0)
        return data[0];
    return data[n]+sum_(n-1);
}
int main()
{
     
    scanf("%d",&N);
    for(i=0; i<N; i++)
        scanf("%d",&data[i]);
    printf("%d\n",sum(0,N-1));
    printf("%d",sum_(N-1));
    return 0;
}

例题2

汉诺塔问题

思路

将汉诺塔的盘子从上到下从1~n进行编号，每次进行操作时，类比只有两个盘的情况，即目标盘与非目标盘，柱子分为起始柱、辅助柱、目标柱，注意，在递归中，三者没有固定对应哪个柱子，对应关系是变化的，对每一次移动过程（把第n个盘从A移动到C上）时，将非目标盘从起始柱通过目标柱移动到辅助柱上，随后将目标盘从起始柱通过辅助柱移动到目标柱上。

当函数中有多层递归的时候，我们可以主观地认为先前的递归已经进行完成，等到该层已经结束后，再来看本层涉及到的其他递归。

代码

void Hanoi(int n,char a,char b,char c)
{
     
	if(n==1)
		printf("move %d %c->%c\n",n,a,c);//如果当前移动的是第1个圆盘，直接从将它从起始盘移动到目标盘
	else
	{
     
		Hanoi(n-1,a,c,b);//将非目标盘移动到辅助柱上
		printf("move %d %c->%c\n",n,a,c);//这个时候目标盘可以直接从起始到目标了
		Hanoi(n-1,b,a,c);//将非目标盘通过起始盘移动到目标盘上
	}
}

快速排序

教材P145（右上）

快速排序的核心思想便是递归与分治，每次以分割元素为基准，比它大的元素放在左（右）边，比它小的元素放在右（左）边，此时分割元素便位于正确的位置，之后再对分隔元素的左区间与右区间排序，直到整个序列有序。

每次排序时，给出所需要的排序区间，以序列中最左端的元素为分割元素，我们想要的是分割元素的左边都小于它，右边都大于它，也就是说我们需要把右边小于分割元素的值移到左边，左边大于分割元素的值移到右边，代码如下

void QuickSort(int left,int right)
{
     
    if(left>right)
        return;
    int i=left,j=right,temp=Data[left];
    while(i!=j)//相遇的时候代表满足左小右大
    {
     
        while(i<j&&Data[j]>=temp)j--;//先从右向左，思考一下为什么一定要遵循这样的顺序？
        while(i<j&&Data[i]<=temp)i++;//再从左向右
        if(i<j)
        	swap(Data[i],Data[j]);
    }
    Data[left]=Data[i];
    Data[i]=temp;
    QuickSort(left,i-1);
    QuickSort(i+1,right);
    return;
}

如果先从左向右，左标记会略过小于分割元素的值，如果此时从左标记到序列边界的区间无小于分割元素的值，右标记势必会与左标记相遇，交换后，分割元素的左边既有大于自身的值，又有小于自身的值

指针和数组

数组在内存中是一块连续开辟的内存空间，指针是用来存储地址的变量，两者有着千丝万缕的联系。

数组指针

在平常的编程当中，数组是这样申请的

int N=100;
int a[N],i;
for(i=0;i<100;i++)
	...

对于数组a来说，a是这个数组的名字，也是这个数组的首地址，使用字符数组可以更好理解这个问题。

char a[100]={
     '\0'};
scanf("%s",a);

这里的a不需要&来取地址，因为a本身就代表了数组的首地址。

接下来，有了前面的铺垫，让我们思考一下什么是数组指针。

数组是一块连续的内存空间，每个元素都有其对应的地址，首个元素的地址与整个数组的首地址相同，如果设置一个指针变量指向数组的首地址，那么这个指针变量便是数组指针。

int a[100]={
     0},*p=NULL;
p=a;//p=&a[0];
for(int i=0;i<100;i++)
{
     
	scanf("%d",p++);
}
p=a;
for(int i=0;i<100;i++)
{
     
	printf("%d",*p);
	p++;
}

数组指针本质上还是一个指针变量，只不过因为它被用于数组，才得以命名，使用的时候以指针与所指变量的关系来理解。

指针数组

指针数组，顾名思义，即元素类型为指针的数组，该数组存储的是指针所对应变量的地址，类比整型数组等概念可以更好地理解。

如图

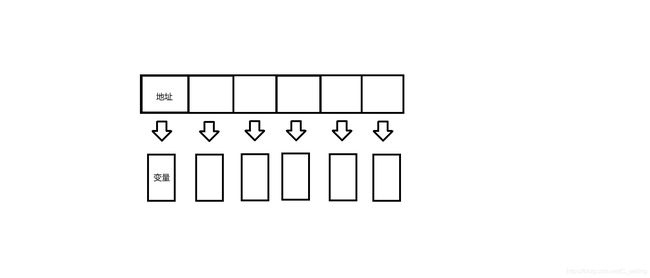
对于指针数组来说，数组为容器，指针不过是里面装的东西罢了，而对于数组元素的操作，对于指针数组即是对指针的操作。

常用做题技巧

在编程过程中，有许多的技巧能为我们提供方便，可以简化代码量、减少手动输入、更清晰地观察运行过程等。

初始设定

1. 尽量使用全局变量
2. 尽量申请较大的内存空间
3. 尽量把调用函数写在main函数之前
4. 初始化和清空

利用库函数

1. atoi
   
2. qsort

int compare(const void* a,const void* b)
{
     
	int*a_=(int*)a;
	int*b_=(int*)b;
	return *a>*b;
}
qsort(data,100,sizeof(int),compare);

3. sqrt

4. strstr

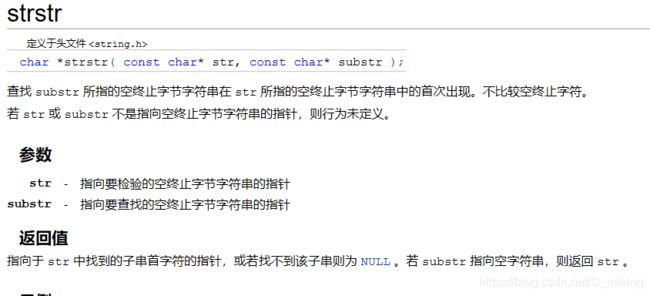
5. pow

6. freopen

freopen("test.txt","r",stdin);

7. memset

8. isdigit/isalpha


9. floor

输出步骤

每当遇到错误时，如果debug不熟练或者涉及到递归，可以考虑在程序运行的时候添加输出函数，将每次运行的结果展示出来，再来判断哪里出现了问题。

常见错误规避

符号

1. &
2. %f、%d、%lf、%ld、%lld
3. ;
5. \n

变量

1. i、j
2. 全局还是局部
3. 是否进行了清空

逻辑错误

杀器——Debug。

拓展

递归的优化

求斐波那契数列是递归中常用的例子，一般来讲，最简单的写法如下

int Fibonacci(int n)
{
     
    if(n==1||n==2)
        return 1;
    return Fibonacci(n-1)+Fibonacci(n-2);
}

这样的写法包含了大量的重复运算（如n=3的斐波那契值已经算出，但是求n=5的斐波那契值又会重新算一次n=3的斐波那契值），效率并不高。

我们可以改进这种写法，对于这个函数，效率最低的地方便是每次都要计算重复的数值，如果我们能够存储已经计算出的数值，该算法的效率将会大大提高，代码如下

int F[121212]={
     1,1};
int Fibonacci_optimized(int n)
{
     
    if(F[n])
        return F[n];
    return F[n]=Fibonacci_optimized(n-1)+Fibonacci_optimized(n-2);
    //思考一下，这里实现了什么？
}

像这种使用先前的推导来推出现在的结果的方法是动态规划算法的思想，有兴趣可以自行了解。

递归与递推

递归和递推可以相互转换，一般来讲，递推的效率高于递归，但是代码量大于递归，还是以斐波那契数列为例，求出某一项的斐波那契值，代码如下

int Fibonacci_recursion(int n)
{
     
    if(n<3)
        return 1;
    int i=0,tmp=0,a=1,b=1;
    for(i=0;i>n-3;i++)
    {
     
        tmp=a+b;
        a=b;
        b=tmp;
    }
    return tmp;
}

总结

本次课程针对递归、快速排序、数组指针与指针数组进行了讲解，并且针对考试介绍了一些应试技巧。

参考文献

1. 《C语言程序设计现代方法》
2. 《啊哈算法》
3. 图解汉诺塔问题（递归求解）
4. C语言指针数组和数组指针–精讲
5. 快速排序法为什么一定要从右边开始的原因