详述Deep Learning中的各种卷积(一)
作者:Redflashing
本文梳理举例总结深度学习中所遇到的各种卷积,帮助大家更为深刻理解和构建卷积神经网络。
本文将详细介绍以下卷积概念:
- 2D卷积(2D Convolution)
- 3D卷积(3D Convolution)
- 1 ∗ 1 1*1 1∗1卷积( 1 ∗ 1 1*1 1∗1 Convolution)
- 反卷积(转置卷积)(Transposed Convolution)
- 扩张卷积(Dilated Convolution / Atrous Convolution)
- 空间可分卷积(Spatially Separable Convolution)
- 深度可分卷积(Depthwise Separable Convolution)
- 平展卷积(Flattened Convolution)
- 分组卷积(Grouped Convolution)
- 混洗分组卷积(Shuffled Grouped Convolution)
- 逐点分组卷积(Pointwise Grouped Convolution)
1. 首先,什么是卷积?
在数学(特别是数学分析)中,卷积是一种重要的运算。卷积应用广泛于信号和图像处理以及其他工程科学领域中。深度学习中的卷积神经网络(CNN)就得名于卷积概念。深度学习中卷积的本质是信号和图像处理中的互相关(Cross-correlation)。在信号/图像处理中,卷积定义如下:
连续情况下:
( f ∗ g ) ( t ) = d e f ∫ − ∞ ∞ f ( τ ) g ( t − τ ) d τ (f * g)(t) \ \ \stackrel{\mathrm{def}}{=}\ \int_{-\infty}^\infty f(\tau) g(t - \tau) \, d\tau (f∗g)(t) =def ∫−∞∞f(τ)g(t−τ)dτ
离散情况下:
( f ∗ g ) [ n ] = d e f ∑ m = − ∞ ∞ f [ m ] g [ n − m ] = ∑ m = − ∞ ∞ f [ n − m ] g [ m ] (f * g)[n]\ \ \stackrel{\mathrm{def}} {=}\ \sum_{m=-\infty}^{\infty} {f[m] g[n-m]} = \sum_{m=-\infty}^\infty f[n-m]\, g[m] (f∗g)[n] =def ∑m=−∞∞f[m]g[n−m]=∑m=−∞∞f[n−m]g[m]
1.1. 卷积和互相关(Cross-correlation)的关系
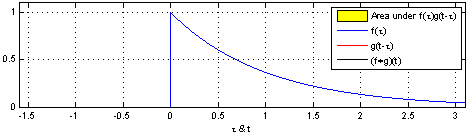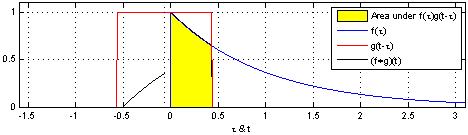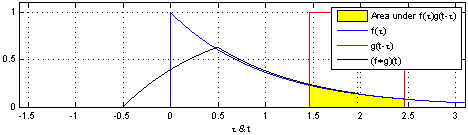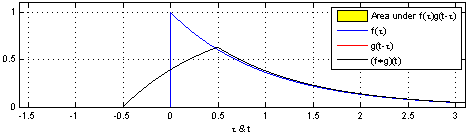
卷积是透过两个函数 f f f和 g g g生成第三个函数的一种数学算子,表征函数 f f f与经过翻转和平移的 g g g的乘积函数所围成曲边梯形的面积。
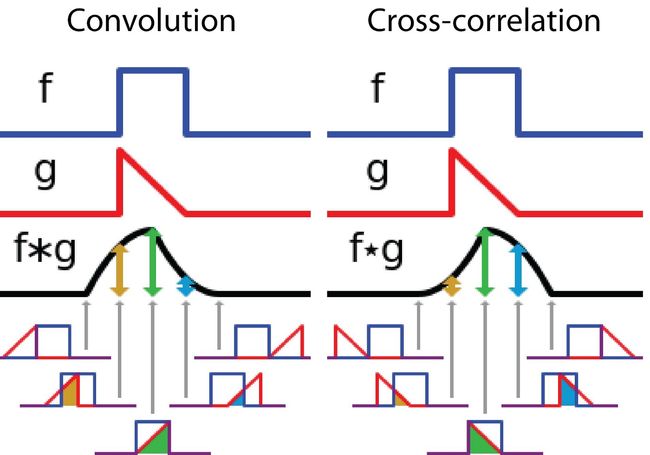
上图(来源:维基百科)为RC电路中的方形脉冲波 g g g(过滤器)和指数衰减 f f f的脉冲波的卷积 ,同样地重叠部分的面积就相当于 t t t处的卷积值。
而互相关是两个函数之间的滑动点积或滑动内积。互相关中的过滤不经过反转,而是直接滑过函数 f f f。 f f f与 g g g之间的交叉区域即是互相关。下图(来源:维基百科)显示了相关性和互相关性的区别。
由此可见,互相关性中的过滤器不会反转。严格意义上来说,深度学习中的“卷积”是互相关(Cross-correlation)运算,本质上执行逐元素乘法和加法。但在之所以习惯性上将其称为卷积,是因为过滤器的权值是在训练过程中学习得到的。如果上面例子中的反转函数 g g g是正确的函数,那么经过训练后,学习得到的过滤器看起来就会像是反转后的函数 g g g。因此在训练之前,没必要像真正的卷积那样首先反转过滤器。
1.2. 深度学习中的卷积
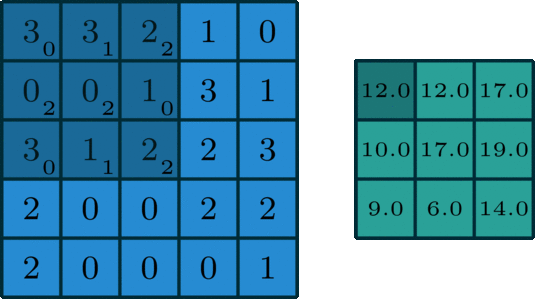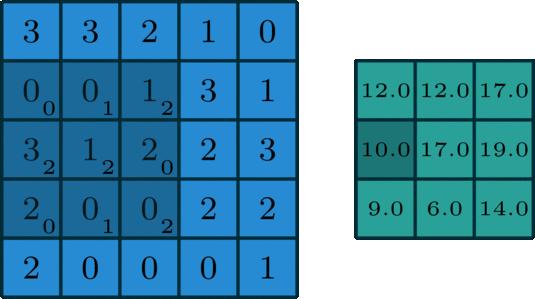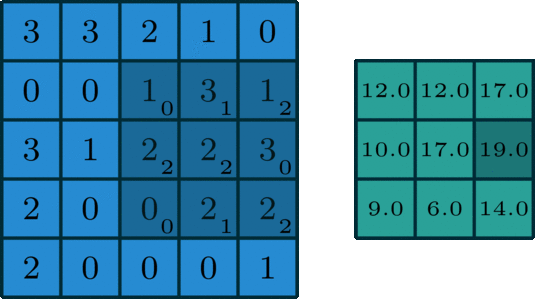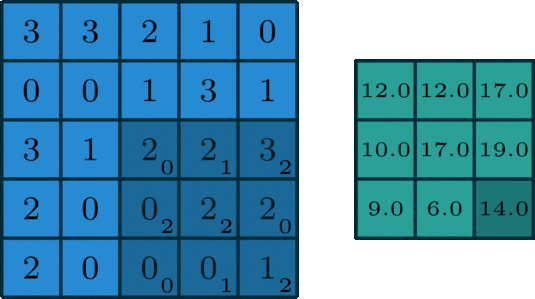
执行卷积的目的是从输入中提取出有用的特征。在图像处理中,有多种过滤器可供选择。不同的滤波器可以提取中不同的特征。如水平、垂直、对角线边缘特征等。在卷积神经网络(CNN)中,通过卷积提取不同的特征,滤波器的权值在训练期间进行学习。然后将提取到的特征复合得到最后的结果。之所以采用卷积的原因在于卷积运算具有权重共享和平移不变形并且卷积还考虑到了像素空间的联系,卷积的这些特性使得其在计算机视觉任务中具有出色的表现。下图(来源:Towards Data Science)展示了单通道图下卷积(也称为标准卷积)的计算过程。
上图输入为 5 ∗ 5 5*5 5∗5的矩阵,滤波器为 3 ∗ 3 3*3 3∗3的矩阵[[0,1,2],[2,2,0],[0,1,2]],滑动步长Stride=1,填充值Padding=0,输出为 3 ∗ 3 3*3 3∗3的矩阵。
在大多数应用中,我们一般需要处理多通道图片。最典型的就是RGB图像。如下图(来源:Andre Mouton)为RGB图像分解的单通道图。
另一个多通道数据的例子是CNN中的层。卷积层通常由多个甚至上百个通道组成。每个通道描述上层的不同特征。如何将通道数不同的层之间进行转换?即如何将通道数为 n n n的层转换为通道数为 m m m的层?
在描述上述问题我们需要先介绍一些术语:Layers(层)、Channels(通道)、Feature Maps(特征图)、Filters(滤波器)、Kernels(卷积核)。从层次结构的角度来看,层和滤波器的概念处于同一水平,而通道和卷积核在下一级结构中。通道和特征图是同一个概念。一层可以有多个通道(或者说特征图)。如果输入的为一个RGB图像,那么就会有3个通道。通道(Channel)通常被用来描述层(Layer)的结构。相似地,卷积核(Kernel)是被用来描述滤波器(Filter)的结构。下图可直观体现层和通道的关系。
滤波器和卷积核的区别有点难以理解。两者在某些情况下可以互换,故可能造成我们的混淆。那两者之间的不同之处在于那些因素呢?卷积核更倾向于2D的权重矩阵。而滤波器则多指的是多个卷积核堆叠的3D结构。若是一个2D的滤波器,那么两者指的是同一个概念。但对于3D滤波器,在大多数深度学习的卷积中,它是包含卷积核的。每个卷积核都是独一无二的,主要在于强调输入的通道的不同部分。
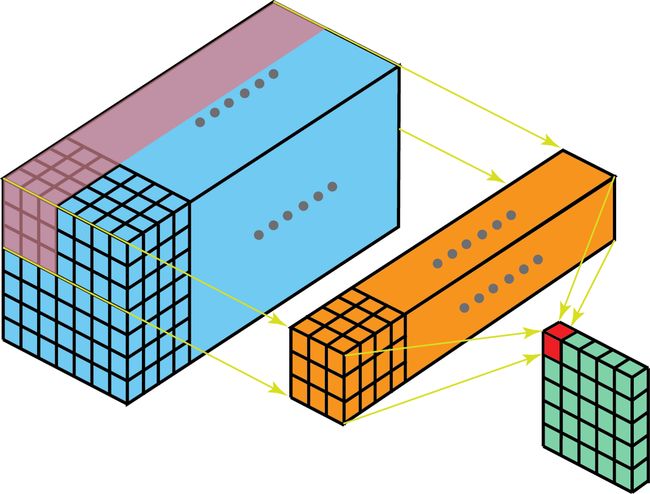
有了以上概念,下面我们继续讲解多通道卷积。每个卷积核都应用于上一层的输入通道,以生成一个输出通道。所有输出通道组合在一起组成输出层。如下图所示:
输入层为 5 ∗ 5 ∗ 3 5*5*3 5∗5∗3的矩阵(即为三通道)。滤波器为 3 ∗ 3 ∗ 3 3*3*3 3∗3∗3的矩阵(即含有3个卷积核)。首先滤波器中的每个卷积核分别应用于输入层的三个通道。执行上次卷积计算,输出3个 3 ∗ 3 3*3 3∗3的通道。
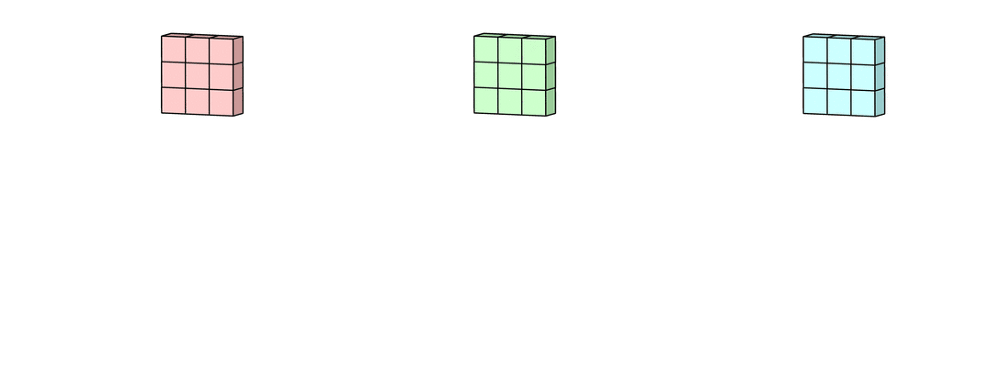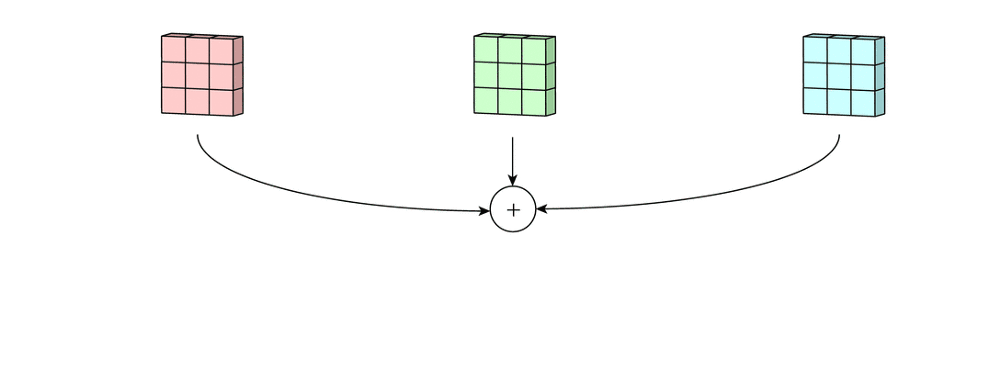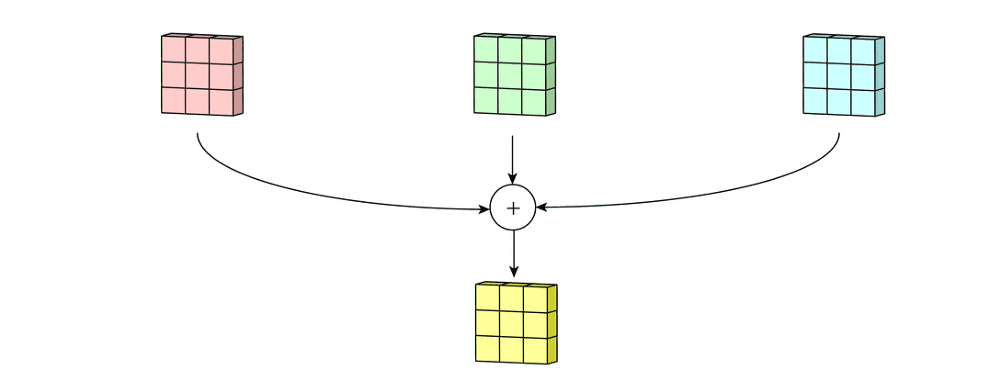
然后对这三通道相加即进行矩阵加法,得到一个 3 ∗ 3 ∗ 1 3*3*1 3∗3∗1的单通道。这个通道就是在输入层( 5 ∗ 5 ∗ 3 5*5*3 5∗5∗3)应用单个滤波器( 3 ∗ 3 ∗ 3 3*3*3 3∗3∗3)的结果。
同样地,以上过程可以更为统一地看成一个3D的滤波器对输入层进行处理。其中输入层和滤波器有着相同的深度,即输入层的通道数量与滤波器中卷积核数量相同。3D滤波器即只需要在输入层(如图像)的2个维度高和宽滑动(这也是为什么3D滤波器用于处理3D矩阵时,该运算过程称为2D卷积的原因)。在每个滑动位置,执行乘法和加法运算得到一个运算结果(单个数字)。在下面的例子中,滑动在 5 ∗ 5 ∗ x 5*5*x 5∗5∗x的输入层( x x x为任意值),最后得到的输出层仅含一个输出通道。
进一步地,我们就能非常轻易地理解如何在不同深度的层(Layer)进行转换。假设输入层有 X i n X_{in} Xin个通道,而输出层需要得到 D o u t D_{out} Dout个通道。只需要将 D o u t D_{out} Dout个过滤器对输入层进行处理,而每一个过滤器有 D i n D_{in} Din个卷积核。每个过滤器提供一个输出通道。完成该过程,将得到 D o u t D_{out} Dout个通道组成输出层。
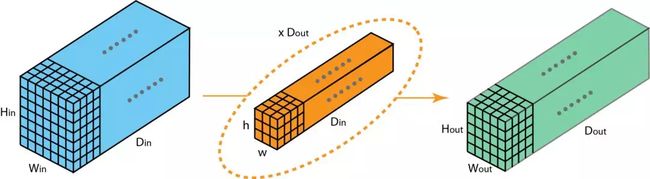
1.3. 2D卷积的计算
输入层: W i n ∗ H i n ∗ D i n W_{in}*H_{in}*D_{in} Win∗Hin∗Din
超参数:
- 过滤器个数: k k k
- 过滤器中卷积核维度: w ∗ h w*h w∗h
- 滑动步长(Stride): s s s
- 填充值(Padding): p p p
输出层: W o u t ∗ H o u t ∗ D o u t W_{out}*H_{out}*D_{out} Wout∗Hout∗Dout
其中输出层和输入层之间的参数关系为,
{ W o u t = ( W i n + 2 p − w ) / s + 1 , H o u t = ( H i n + 2 p − h ) / s + 1 , D o u t = k \begin{cases} W_{out} = (W_{in} +2p - w)/s + 1 ,\\ H_{out} = (H_{in} +2p - h)/s + 1, \\ D_{out} = k \end{cases} ⎩⎪⎨⎪⎧Wout=(Win+2p−w)/s+1,Hout=(Hin+2p−h)/s+1,Dout=k
参数量为: ( w ∗ h ∗ D i n + 1 ) ∗ k (w*h*D_{in} + 1)*k (w∗h∗Din+1)∗k
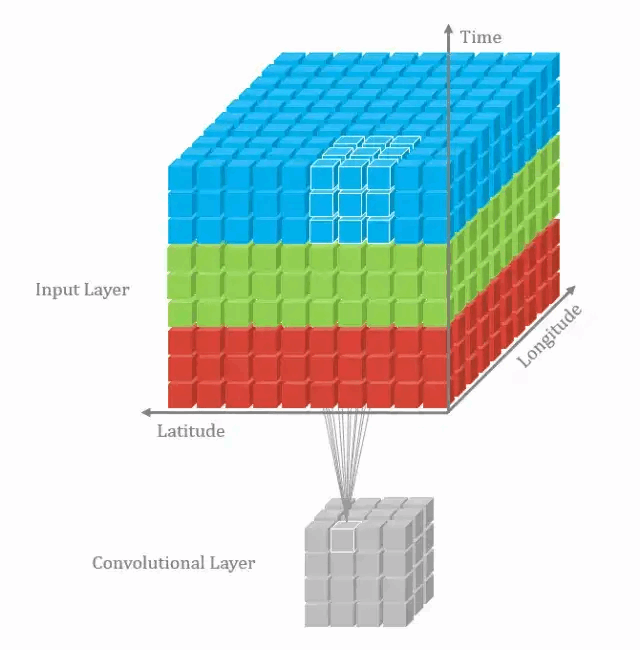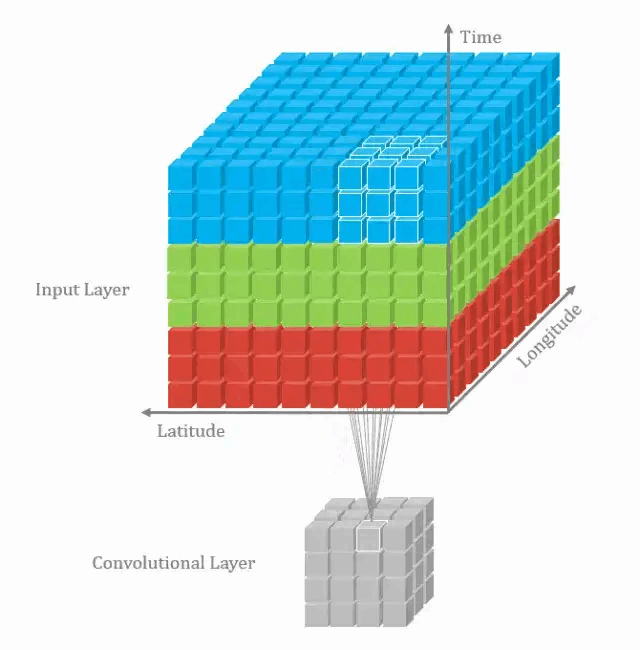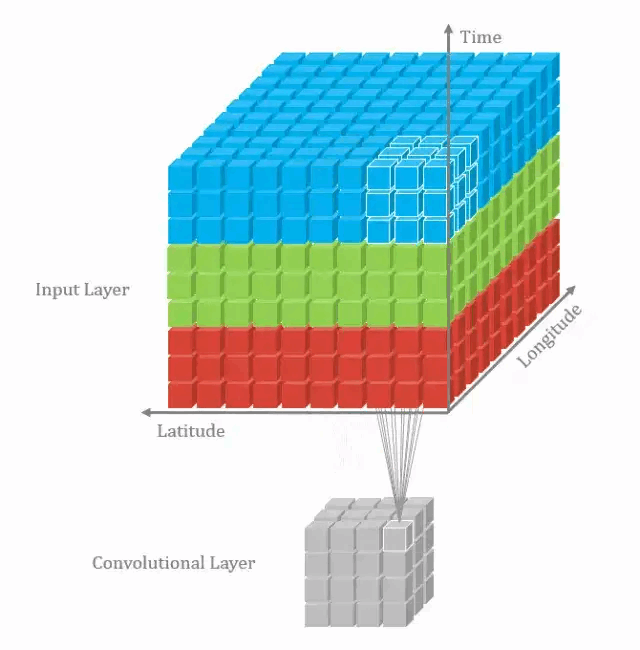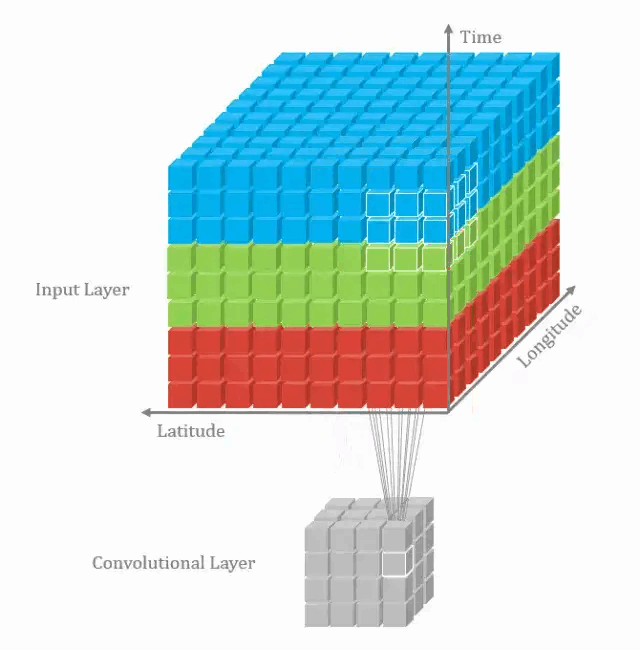
2. 3D卷积
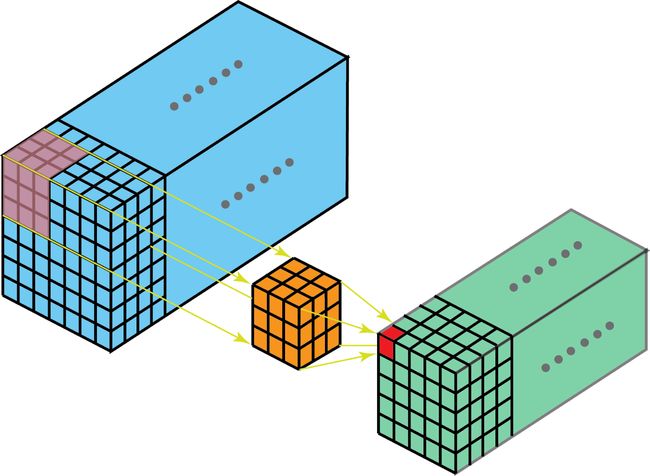
在上一个插图中,可以看出,这实际上是在完成3D卷积。但通常意义上,仍然称之为深度学习的2D卷积。因为将滤波器深度和输入层深度相同,3D滤波器仅在2个维度上移动(例如图像的高度和宽度),得到的结果为单通道。
通过将2D卷积的推广,在3D卷积定义为滤波器的深度小于输入层的深度(即卷积核的个数小于输入层通道数),故3D滤波器需要在三个维度上滑动(输入层的长、宽、高)。在滤波器滑动的每个位置执行一次卷积操作,得到一个数值。当滤波器滑过整个3D空间,输出的结构也是3D的。
2D卷积和3D卷积的主要区别为滤波器滑动的空间维度。3D卷积的优势在于描述3D空间中的对象关系。3D关系在某一些应用中十分重要,如3D对象的分割以及医学图像的重构等。
2.1. 3D卷积的计算
输入层: W i n ∗ H i n ∗ D i n ∗ C i n W_{in}*H_{in}*D_{in}*C_{in} Win∗Hin∗Din∗Cin
超参数:
- 过滤器个数: k k k
- 过滤器中卷积核维度: w ∗ h ∗ d w*h*d w∗h∗d
- 滑动步长(Stride): s s s
- 填充值(Padding): p p p
输出层: W o u t ∗ H o u t ∗ D o u t ∗ C o u t W_{out}*H_{out}*D_{out}*C_{out} Wout∗Hout∗Dout∗Cout
其中输出层和输入层之间的参数关系为,
{ W o u t = ( W i n + 2 p − w ) / s + 1 , H o u t = ( H i n + 2 p − h ) / s + 1 , D o u t = ( D i n + 2 p − d ) / s + 1 , C o u t = k \begin{cases} W_{out} = (W_{in} +2p - w)/s + 1 ,\\ H_{out} = (H_{in} +2p - h)/s + 1, \\ D_{out} = (D_{in} +2p - d)/s + 1, \\ C_{out} = k \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧Wout=(Win+2p−w)/s+1,Hout=(Hin+2p−h)/s+1,Dout=(Din+2p−d)/s+1,Cout=k
参数量为: ( w ∗ h ∗ d + 1 ) ∗ k (w*h*d + 1)*k (w∗h∗d+1)∗k
3. 1 ∗ 1 1*1 1∗1卷积
1 ∗ 1 1*1 1∗1卷积十分有趣。咋一看 1 ∗ 1 1*1 1∗1卷积对于单通道而言仅仅是每个元素乘以一个数字,但如果输入层为多通道,情况就变为有趣了。
上图解释了 1 ∗ 1 1*1 1∗1卷积如何适用于尺寸为 H ∗ W ∗ D H*W*D H∗W∗D的输入层,滤波器大小为 1 ∗ 1 ∗ D 1*1*D 1∗1∗D,输出通道的尺寸为 H ∗ W ∗ 1 H*W*1 H∗W∗1。如果应用 n n n个这样的滤波器,然后组合在一起,得到的输出层大小为 H ∗ W ∗ n H*W*n H∗W∗n。
3.1. 1 ∗ 1 1*1 1∗1卷积的作用
-
调节通道数
由于 1 × 1 1×1 1×1 卷积并不会改变 height 和 width,改变通道的第一个最直观的结果,就是可以将原本的数据量进行增加或者减少。这里看其他文章或者博客中都称之为升维、降维。但实际情况维度并没有改变,改变的只是 h e i g h t × w i d t h × c h a n n e l s height × width × channels height×width×channels 中的 c h a n n e l s channels channels这一个维度的大小而已。
-
增加非线性
1 ∗ 1 1*1 1∗1卷积核,可以在保持特征图尺度不变的(即不改变)的前提下大幅增加非线性特性(利用后接的非线性激活函数如ReLU)。非线性允许网络学习更复杂的功能,并且使得整个网络能够进一步加深。
-
跨通道信息
使用 1 ∗ 1 1*1 1∗1卷积核,实现降维和升维的操作其实就是间通道信息的线性组合变化。例如:在卷积核大小为 3 ∗ 3 3*3 3∗3,卷积核个数为64的滤波器与卷积核大小为 1 ∗ 1 1*1 1∗1,卷积核个数为28的滤波器组合,其输出层大小等于通过卷积核大小为 3 ∗ 3 3*3 3∗3,卷积核个数为28的滤波器所得到的输出层的大小,原来的64个通道就可以理解为跨通道线性组合变成了28通道,这就是通道间的信息交互。
-
减少参数
前面所说的降维,其实也是减少了参数,因为特征图少了,参数也自然跟着就减少,相当于在特征图的通道数上进行卷积,压缩特征图,二次提取特征,使得新特征图的特征表达更佳。
关于 1 ∗ 1 1 * 1 1∗1卷积的一个有趣的观点来自 Yann LeCun, “在卷积神经网络中, 没有‘全连接层(fully-connected layers)’的概念。只有卷积层具有 1 ∗ 1 1*1 1∗1卷积核和全连接表。”
3.2. 1 ∗ 1 1*1 1∗1卷积的应用
1 ∗ 1 1*1 1∗1卷积在多个经典网络中发挥了重要作用,以下简要介绍几个 1 ∗ 1 1*1 1∗1卷积重要的应用。
-
Network in Network(NIN)
NIN提出了MLP卷积层,MLP卷积层通过叠加"Micro Network"网络,提高非线性表达,而其中的"Micro Network"基本组成单元是 1 ∗ 1 1*1 1∗1卷积网路,说到这,就要解释一下 1 ∗ 1 1*1 1∗1卷积了,该篇论文是首次提出 1 ∗ 1 1*1 1∗1卷积,具有划时代的意义,之后的GoogleNet借鉴了 1 ∗ 1 1*1 1∗1卷积,还专门致谢过这篇论文。
-
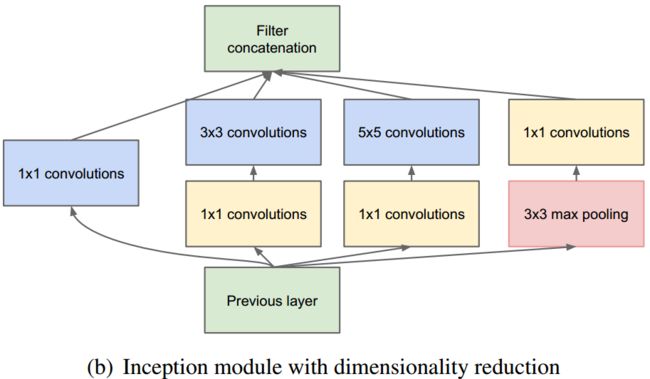
Inception
GoogleNet首次提出Inception模块,Inception一共有V1、V2、V3、V4四个版本(这里就不详述了)。下图为Inception V1的结构如下图两个图所示。
在充分引入 1 ∗ 1 1*1 1∗1卷积进行降维后如图(b)所示,总体而言相比于图(a)其卷积参数量已经减少了近4倍。
在inception结构中,大量采用了 1 ∗ 1 1*1 1∗1卷积,主要是两点作用:a.对数据进行降维;b.引入更多的非线性,提高泛化能力,因为卷积后要经过ReLU激活函数;
-
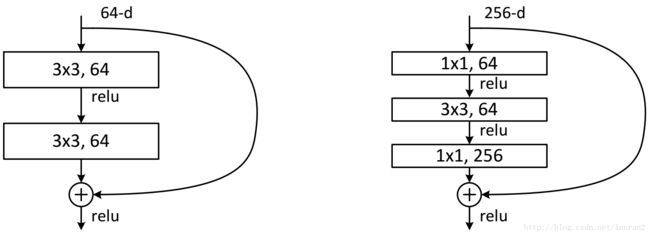
ResNet
ResNet同样也利用了 1 ∗ 1 1*1 1∗1卷积,并且是在 3 ∗ 3 3*3 3∗3卷积层的前后都使用了,不仅进行了降维,还进行了升维,参数数量进一步减少。其中右图又称为Bottleneck Design,目的一目了然,就是为了降低参数的数目,第一个 1 ∗ 1 1*1 1∗1的卷积把通道量从256降到64,然后在最后通过 1 ∗ 1 1*1 1∗1卷积恢复,整体上用的参数数目差了近16.94倍。
对于常规ResNet,可以用于34层或者更少的网络中,对于Bottleneck Design的ResNet通常用于更深的如101这样的网络中,目的是减少计算和参数量。
3.3. 1 ∗ 1 1*1 1∗1卷积的计算
1 ∗ 1 1*1 1∗1卷积实际上看做2D卷积的特殊情况,计算的过程可参考2D卷积的计算过程。
4. Convolution Arithmetic
现在我们知道了Depth维度的卷积。我们继续学习另外两个方向(Height&Width),同样重要的卷积算法。一些术语:
-
Kernel size(卷积核尺寸):卷积核在上面的部分已有提到,卷积核大小定义了卷积的视图。
-
Stride(步长):定义了卷积核在图像中移动的每一步的大小。比如Stride=1,那么卷积核就是按一个像素大小移动。Stride=2,那么卷积核在图像中就是按2个像素移动(即,会跳过一个像素)。我们可以用stride>=2,来对图像进行下采样。
-
Padding:可以将Padding理解为在图像外围补充一些像素点。padding可以保持空间输出维度等于输入图像,必要的话,可以在输入外围填充0。另一方面,unpadded卷积只对输入图像的像素执行卷积,没有填充0。输出的尺寸将小于输入。
参考资料
-
A Comprehensive Introduction to Different Types of Convolutions in Deep Learning | by Kunlun Bai | Towards Data Science
-
Convolutional neural network - Wikipedia
-
Convolution - Wikipedia
-
一文读懂卷积神经网络中的1x1卷积核 - 知乎 (zhihu.com)
-
[1312.4400] Network In Network (arxiv.org)
-
Inception网络模型 - 啊顺 - 博客园 (cnblogs.com)
-
ResNet解析_lanran2的博客-CSDN博客
-
一文带你了解深度学习中的各种卷积(上) | 机器之心 (jiqizhixin.com)
-
Intuitively Understanding Convolutions for Deep Learning | by Irhum Shafkat | Towards Data Science
- An Introduction to different Types of Convolutions in Deep Learning
- Review: DilatedNet — Dilated Convolution (Semantic Segmentation)
- ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices
- Separable convolutions “A Basic Introduction to Separable Convolutions
- Inception network “A Simple Guide to the Versions of the Inception Network”
- A Tutorial on Filter Groups (Grouped Convolution)
- Convolution arithmetic animation
- Up-sampling with Transposed Convolution
oup-tutorial/) - Convolution arithmetic animation
- Up-sampling with Transposed Convolution
- Intuitively Understanding Convolutions for Deep Learning