详述Deep Learning中的各种卷积（三）
作者：Redflashing
本文梳理举例总结深度学习中所遇到的各种卷积，帮助大家更为深刻理解和构建卷积神经网络。
本文将详细介绍以下卷积概念：
- 2D卷积（2D Convolution）
- 3D卷积（3D Convolution）
- 1 ∗ 1 1*1 1∗1卷积（ 1 ∗ 1 1*1 1∗1 Convolution）
- 反卷积（转置卷积）(Transposed Convolution）
- 扩张卷积（Dilated Convolution / Atrous Convolution)
- 空间可分卷积（Spatially Separable Convolution）
- 深度可分卷积（Depthwise Separable Convolution）
- 平展卷积（Flattened Convolution）
- 分组卷积（Grouped Convolution）
- 混洗分组卷积（Shuffled Grouped Convolution）
- 逐点分组卷积（Pointwise Grouped Convolution）
7. 可分卷积（Separable Convolution）
在一些经典网络架构中可分卷积发挥了重要的作用，比如MobileNets。可分卷积又可分为空间可分卷积核深度可分卷积。
7.1. 空间可分卷积（Spatially Separable Convolution）
空间可分卷积根据图像宽核高的2D空间尺寸进行操作。从概念上来讲，空间可分卷积将卷积分解为两个独立的操作。我们拿数字图像处理中常见的 3 ∗ 3 3*3 3∗3索贝尔算子（Sobel operator，主要用于边缘检测）分解为 3 ∗ 1 3*1 3∗1和 1 ∗ 3 1*3 1∗3卷积核。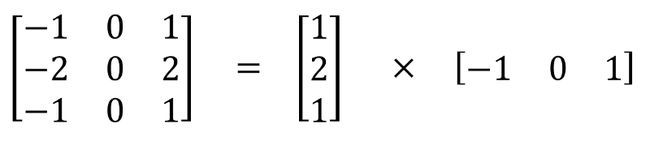
在卷积中， 3 ∗ 3 3*3 3∗3卷积核直接与图像卷积进行卷积运算（具体过程可参考转置卷积中计算机中如何处理卷积运算）。在空间可分卷积中， 3 ∗ 1 3*1 3∗1卷积核先于图像进行卷积再应用 1 ∗ 3 1*3 1∗3卷积核。执行相同的操作时，相比于直接卷积运算需要9个参数这样仅需要6个参数。
此外，在空间可分卷积中相比于正常卷积所进行的矩阵乘法次数也更少。下面给出一个具体的例子， 5 ∗ 5 5*5 5∗5图像经过 3 ∗ 3 3*3 3∗3卷积核（步长为1，填充为0），水平滑动3个位置，垂直滑动3个位置。一共滑动9个位置，在每个位置9个元素进行逐个乘法。所以总共要执行 9 ∗ 9 = 81 9*9=81 9∗9=81乘法运算。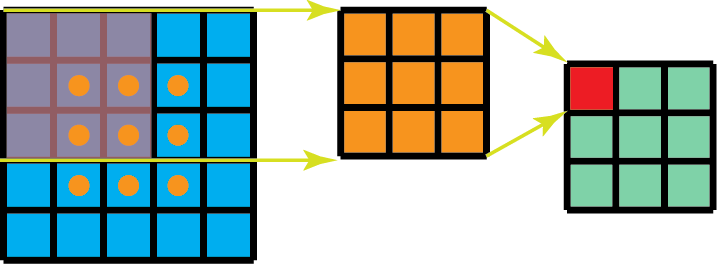
另一方面，对于空间可分卷积，我们首先对 5 ∗ 5 5*5 5∗5的图像应用 3 ∗ 1 3*1 3∗1卷积核。在水平滑动5个位置以及垂直滑动3个位置即 5 ∗ 3 = 15 5*3=15 5∗3=15个位置，在每个位置完成3次乘法运算，总共是 15 ∗ 3 = 45 15*3=45 15∗3=45次乘法运算。再将得到的 3 ∗ 5 3*5 3∗5的输出应用 1 ∗ 3 1*3 1∗3卷积核。那么需要水平滑动3个位置和垂直扫描3个位置，总共9个位置，每个位置完成3次乘法运算，那么总共要执行 9 ∗ 3 = 27 9*3=27 9∗3=27次乘法运算，所以上述空间可分卷积一共完成 45 + 27 = 72 45+27=72 45+27=72次乘法运算，相比于正常卷积乘法运算减少了。
这里我们来归纳一下上面的例子。现在我们应用卷积在一共 n ∗ n n*n n∗n图像上，卷积核为 m ∗ m m*m m∗m，步长为1，填充为0。
-
标准卷积计算成本：
( n − 2 ) ∗ ( n − 2 ) ∗ m ∗ m (n-2)*(n-2)*m*m (n−2)∗(n−2)∗m∗m
-
空间可分卷积计算成本：
n ∗ ( n − 2 ) ∗ m + ( n − 2 ) ∗ ( n − 2 ) ∗ m = ( 2 n − 2 ) ∗ ( n − 2 ) ∗ m n*(n-2)*m+(n-2)*(n-2)*m\\=(2n-2)*(n-2)*m n∗(n−2)∗m+(n−2)∗(n−2)∗m=(2n−2)∗(n−2)∗m
-
空间可分卷积与标准卷积的计算成本之比为：
2 m + 2 m ∗ ( n − 2 ) \dfrac{2}{m} + \dfrac{2}{m*(n-2)} m2+m∗(n−2)2
对于图像大小 n n n大于卷积核大小的情况（ n > > m n>>m n>>m）,此时比值变为 2 m \frac{2}{m} m2。这意味着在这种渐进的情况下，当卷积核为 3 ∗ 3 3*3 3∗3，空间可分卷积的卷积计算成本是标准卷积的 2 3 \frac{2}{3} 32。如果为 5 ∗ 5 5*5 5∗5卷积其值为 2 5 \frac{2}{5} 52，如果为 7 ∗ 7 7*7 7∗7卷积其值为 2 7 \frac{2}{7} 72等等。
虽然空间可分卷积可节省成本，但很少用于深度学习。其中一个主要的原因是：并非所有卷积核都可以分成两个较小的卷积核。如果我们用空间可分卷积取代所有传统的卷积，则有可能我们限制自己在训练期间搜索所有可能的内核，导致模型训练结果不尽如人意。
7.2. 深度可分卷积
相比于空间可分卷积，深度可分卷积在深度学习中要常用得多（比如MobileNet和Xception）。深度可分卷积包含两个步骤：深度卷积和 1 ∗ 1 1*1 1∗1卷积。
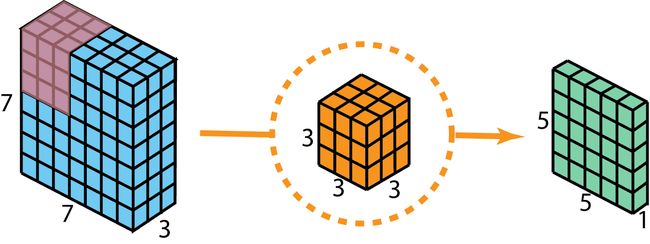
在描述这些步骤前，值得再复习2D卷积和 1 ∗ 1 1*1 1∗1卷积。现在快速回顾一下标准2D卷积。这里举一个具体示例，假设输入为 7 ∗ 7 ∗ 3 7*7*3 7∗7∗3,滤波器为 3 ∗ 3 ∗ 3 3*3*3 3∗3∗3。使用一个滤波器进行2D卷积后，输出层的大小为 5 ∗ 5 ∗ 1 5*5*1 5∗5∗1（只有1个通道）。
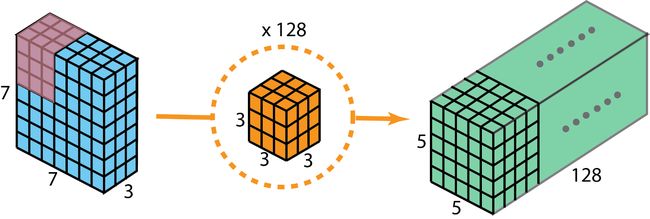
通常，在两个神经网络层之间应用多个过滤器。假设我们这里有128个过滤器。在应用这128个过滤器后得到输出为128个 5 ∗ 5 ∗ 1 5*5*1 5∗5∗1矩阵。堆叠成 5 ∗ 5 ∗ 128 5*5*128 5∗5∗128。这样做，我们将输入层（ 7 ∗ 7 ∗ 3 7*7*3 7∗7∗3）转换为输出层（ 5 ∗ 5 ∗ 128 5*5*128 5∗5∗128）。空间尺寸（即高度和宽度）收缩，而深度则扩展。
现在，通过深度可分卷积实现相同的转换。
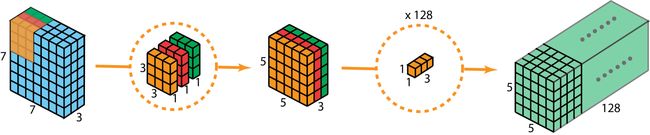
首先，我们将深度卷积应用于输入层。但不是使用大小 3 ∗ 3 ∗ 3 3*3*3 3∗3∗3的2D卷积单个滤波器，我们将单其中3个卷积核分别单独使用。每个卷积核与对应输入层的单个通道进行卷积操作（即省略单个滤波器将输入处理当中的多通道对应位置相加为单通道的过程），则得到一个 5 ∗ 5 ∗ 3 5*5*3 5∗5∗3的输出。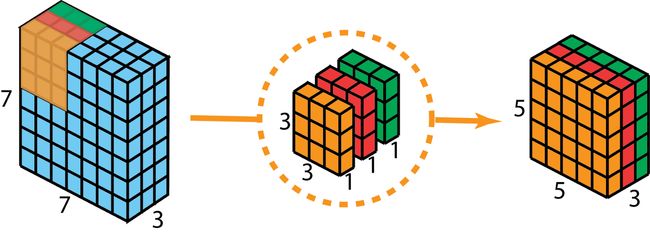
接下来，使用大小为 1 ∗ 1 ∗ 3 1*1*3 1∗1∗3的卷积核，完成 1 ∗ 1 1*1 1∗1卷积。最后得到 5 ∗ 5 ∗ 1 5*5*1 5∗5∗1的输出。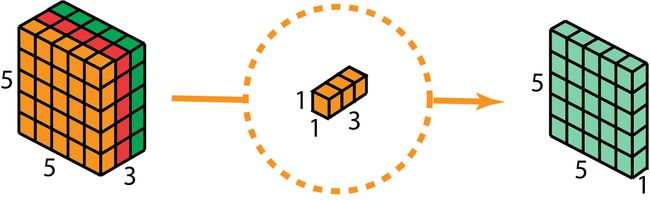
于是我们可以应用128个 1 ∗ 1 1*1 1∗1卷积核，这样我们同样得到一个 5 ∗ 5 ∗ 128 5*5*128 5∗5∗128的输出。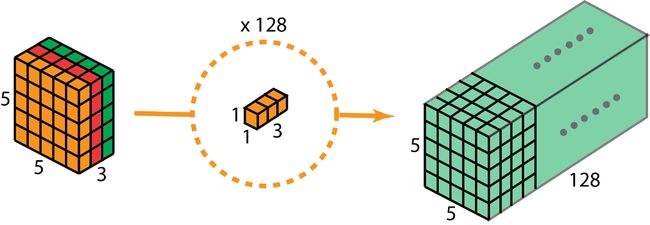
深度可分卷积的操作流程可如下图所示：
那么深度可分卷积相比于普通2D卷积的优势是什么？
深度可分卷积和空间可分卷积的优势一样也是减少了计算成本。与2D卷积相比，深度可分卷积所需的操作要少得多。这里我们以上面的例子来计算。有128个 3 ∗ 3 ∗ 3 3*3*3 3∗3∗3卷积核滑动 5 ∗ 5 5*5 5∗5个位置。即 128 ∗ 3 ∗ 3 ∗ 3 ∗ 5 ∗ 5 = 86400 128*3*3*3*5*5=86400 128∗3∗3∗3∗5∗5=86400次乘法运算。而在可分离卷积中，在步骤一中，有3个 3 ∗ 3 ∗ 1 3*3*1 3∗3∗1卷积核滑动 5 ∗ 5 5*5 5∗5个位置一共进行了 3 ∗ 3 ∗ 3 ∗ 1 ∗ 5 ∗ 5 = 675 3*3*3*1*5*5=675 3∗3∗3∗1∗5∗5=675次乘法运算。在步骤二中，有128个 1 ∗ 1 ∗ 3 1*1*3 1∗1∗3卷积核滑动 5 ∗ 5 5*5 5∗5次一共 128 ∗ 1 ∗ 1 ∗ 3 ∗ 5 ∗ 5 = 9600 128*1*1*3*5*5=9600 128∗1∗1∗3∗5∗5=9600次乘法运算，总体而言深度可分卷积仅需要 675 ∗ 9600 = 10275 675*9600=10275 675∗9600=10275次乘法运算。其计算成本仅仅是2D卷积的 12 % 12\% 12%左右。
同样，我们对深度可分卷积进行归纳。假设输入为 h ∗ w ∗ d h*w*d h∗w∗d，应用 n n n个 h 0 ∗ h 0 ∗ d h_0*h_0*d h0∗h0∗d的滤波器（步长为1，填充为0， h h h为偶数）,同时输出层为 ( h − h 0 + 1 ) ∗ ( w − h 0 + 1 ) ∗ n (h-h_0+1)*(w-h_0+1)*n (h−h0+1)∗(w−h0+1)∗n。
-
2D卷积的计算成本：
n ∗ h 0 ∗ h 0 ∗ d ∗ ( h − h 0 + 1 ) ∗ ( w − h 0 + 1 ) n*h_0*h_0*d*(h-h_0+1)*(w-h_0+1) n∗h0∗h0∗d∗(h−h0+1)∗(w−h0+1)
-
深度可分卷积的计算成本：
d ∗ h 0 ∗ h 0 ∗ 1 ∗ ( h − h 0 + 1 ) ∗ ( w − h 0 + 1 ) + n ∗ 1 ∗ 1 ∗ d ∗ ( h − h 0 + 1 ) ∗ ( w − h 0 + 1 ) = ( h 0 ∗ h 0 + n ) ∗ d ∗ ( h − h 0 + 1 ) ∗ ( w − h 0 + 1 ) d*h_0*h_0*1*(h-h_0+1)*(w-h_0+1) +\\ n*1*1*d*(h-h_0+1)*(w-h_0+1)\\=(h_0*h_0+n)*d*(h-h_0+1)*(w-h_0+1) d∗h0∗h0∗1∗(h−h0+1)∗(w−h0+1)+n∗1∗1∗d∗(h−h0+1)∗(w−h0+1)=(h0∗h0+n)∗d∗(h−h0+1)∗(w−h0+1)
-
深度可分卷积和2D卷积所需的计算成本比值为:
1 n + 1 h 0 2 \frac{1}{n}+\frac{1}{h_0^2} n1+h021
目前大多数网络结构的输出层通常都有很多通道，可达数百个甚至上千个。该情况下（ n > > h 0 n>>h_0 n>>h0），则上式可简写为 1 h 0 2 \frac{1}{h_0^2} h021。基于此，如果使用 3 ∗ 3 3*3 3∗3的滤波器，则2D卷积的乘法计算次数比深度可分卷积多9倍。对于 5 ∗ 5 5*5 5∗5的滤波器，2D卷积的乘法次数可能是其25倍。
**使用深度可分卷积有什么缺点吗？**当然有。深度可分卷积可大幅度减少卷积的参数。因此对于规模较小的模型，如果将2D卷积替换为深度可分卷积，其模型大小可能会显著降低，模型的能力可能会变得不太理想，因此得到的模型可能是次优的。但如果使用得当，深度可分卷积能在不牺牲模型性能的前提下显著提高效率。
8.平展卷积（Flattened convolutions）
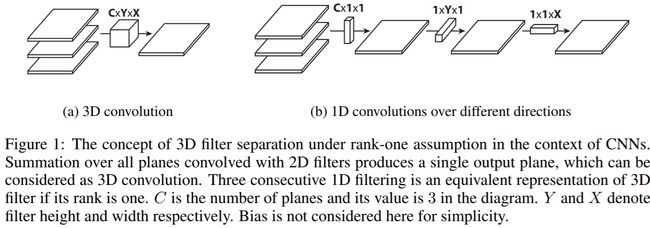
在论文《Flattened convolutional neural networks for feedforward acceleration》中介绍了平展卷积。从直觉上看，平展卷积的理念是滤波器分离。我们不应用一个标准的滤波器将输入映射到输出，而是将此标准的滤波器分解为3个1D滤波器。这种想法与上述空间可分卷积类似，其中的一个空间滤波器近似于两个 rank-1 过滤器（秩1矩阵），而秩1矩阵可表示为一列基乘以一行基的形式 A = U V T A=UV^T A=UVT，最后分解得到3个1D滤波器。
应该注意的是，如果标准滤波器是rank-1滤波器，则此类滤波器就可分为3个1D滤波器的向量积。实际情况中标准滤波器的秩通常大于1。论文中也提到，随着分类问题难度的增加，将平展卷积直接应用于滤波器会导致显著的信息丢失。
为了缓解此类问题，论文对感受野的连接进行限制，以便模型在训练时可以学习分解后的1D滤波器。这篇论文提到，通过使用由连续的 1D 过滤器组成的扁平化网络在 3D 空间的所有方向上训练模型，能够提供的性能与标准卷积网络相当，不过由于学习参数的显著减少，其计算成本要更低得多。
参考资料
-
A Comprehensive Introduction to Different Types of Convolutions in Deep Learning | by Kunlun Bai | Towards Data Science
-
Convolutional neural network - Wikipedia
-
Convolution - Wikipedia
-
一文读懂卷积神经网络中的1x1卷积核 - 知乎 (zhihu.com)
-
[1312.4400] Network In Network (arxiv.org)
-
Inception网络模型 - 啊顺 - 博客园 (cnblogs.com)
-
ResNet解析_lanran2的博客-CSDN博客
-
一文带你了解深度学习中的各种卷积（上） | 机器之心 (jiqizhixin.com)
-
Intuitively Understanding Convolutions for Deep Learning | by Irhum Shafkat | Towards Data Science
-
An Introduction to different Types of Convolutions in Deep Learning
-
Review: DilatedNet — Dilated Convolution (Semantic Segmentation)
-
ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices
-
Separable convolutions “A Basic Introduction to Separable Convolutions
-
Inception network “A Simple Guide to the Versions of the Inception Network”
-
A Tutorial on Filter Groups (Grouped Convolution)
-
Convolution arithmetic animation
-
Up-sampling with Transposed Convolution
-
Intuitively Understanding Convolutions for Deep Learning