LeetCode 547. 省份数量 | Python

547. 省份数量

---

题目来源：力扣（LeetCode）https://leetcode-cn.com/problems/number-of-provinces/

题目

---

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

示例 1：

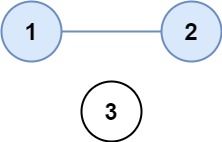
输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例 2：

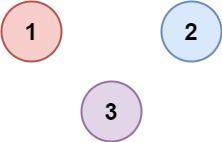
输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

提示：

• 1 <= n <= 200
• n == isConnected.length
• n == isConnected[i].length
• isConnected[i][j] 为 1 或 0
• isConnected[i][i] == 1
• isConnected[i][j] == isConnected[j][i]

解题思路

---

思路：深度优先搜索、广度优先搜索、并查集

先审题，题目中给定 $n$ 个城市，一些彼此相连，一些没有相连。其中有个 省会 的概念，由一组直接或间接相连的城市组成，组内不存在其他没有相连的城市。现在题目要求，省会 的数量？

在这里，我们可以将城市之间的相连关系看成是图，矩阵 $isConnected$ 是图的邻接矩阵，城市是图的节点，相连关系是图中相连的边，而要求的省会即是图中的连通分量，那么问题就变成求图中连通分量的数量。

那么我们可以考虑使用深度优先搜索、广度优先搜索、并查集。

深度优先搜索

先说下深度优先搜索的做法：

• 先声明变量 $visited$ 用以标记城市是否被遍历访问过；
• 遍历所有的城市，若遍历的城市未被访问，那么以此开始深度优先搜索，同时进行标记，直到同一个连通分量中的点都被访问，那表示存在一个省份。
• 若此时还有其他城市未被访问，那么表示有新的连通分量，用 $count$ 存储。继续搜索，直到所有的城市都被访问。最终返回 $count$。

具体的代码实现如下。

class Solution:
    def findCircleNum(self, isConnected: List[List[int]]) -> int:
        def dfs(i):
            """以 i 为起点开始深度优先搜索
            """
            # 先进行标记
            visited[i] = 1
            # 继续搜索与 i 相连的城市
            for j in range(n):
                if isConnected[i][j] == 1 and not visited[j]:
                    dfs(j)


        # 城市数量
        n = len(isConnected)
        # visited 用以标记城市是否被访问
        visited = [0] * n
        # 用以存储省会的数量
        count = 0
        # 开始遍历城市进行搜索
        for i in range(n):
            # 城市未被访问时，开始搜索
            if not visited[i]:
                count += 1
                dfs(i)
        
        return count
            

广度优先搜索

广度优先搜索的思路，与上面深度优先搜索的思路类似。用 $visited$ 标记城市是否曾被访问，遍历城市，若城市未被访问，那么就由该城市开始进行广度优先搜索，知道同一分量的所有城市都被访问，可得到一个省会的数量，用 $count$ 存储。直到所有的城市都被访问，可得省会的总数，返回 $count$。

具体的代码实现如下。

class Solution:
    def findCircleNum(self, isConnected: List[List[int]]) -> int:
        n = len(isConnected)
        # 标记
        visited = [0] * n

        count = 0
        queue = collections.deque()

        # 遍历城市，开始搜索
        for i in range(n):
            if not visited[i]:
                # 更新变量
                visited[i] = 1
                count += 1
                queue.append(i)

                while queue:
                    # 出队开始搜索
                    u = queue.popleft()
                    # 搜索与 u 相连且未被访问的城市
                    for v in range(n):
                        if isConnected[u][v] == 1 and not visited[v]:
                            visited[v] = 1
                            queue.append(v)
            
        return count

并查集

现在问题变成求图中连通分量的数量，我们可以使用并查集的方法。

$n$ 个城市表示图的 $n$ 个点，初始时，令所有的点都指向自身，自成一个连通分量。

遍历矩阵 $isConnected$，如果点与点之间存在相连的关系，那么它们属于同一个连通分量，将点与其邻接点进行合并。

当所有点都遍历后，计算合并后连通分量的总数，返回。

具体的代码实现如下。

class UnionFind:
    """并查集
    """
    def __init__(self, n):
        self.parent = [i for i in range(n)]
        # 初始连通分量数为 n 个
        self.count = n
    
    def find(self, x):
        if x != self.parent[x]:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]
    
    def union(self, u, v):
        u_root = self.find(u)
        v_root = self.find(v)
        # 合并，连通分量数减少
        if u_root != v_root:
            self.parent[u_root] = v_root
            self.count -= 1

class Solution:
    def findCircleNum(self, isConnected: List[List[int]]) -> int:
        n = len(isConnected)
        uf = UnionFind(n)
        for i in range(n):
            for j in range(i+1, n):
                if isConnected[i][j] == 1:
                    # 有相连关系，则进行合并
                    uf.union(i, j)
        return uf.count

欢迎关注

---

公众号 【书所集录】

---

如有错误，烦请指正，欢迎指点交流。若觉得写得还不错，麻烦点个赞，谢谢。