PRAML学习笔记-信息论
PRAML学习笔记-信息论
概述
对<<pattern recognition and machine learning>> 一书关于信息论简介的学习笔记,
对于一个随机变量x,它携带有多少信息量呢?
当我们观察到了x的一个特定值的时候,我们获得了多少信息量呢?
信息量可以表示为“惊讶度”(degree of surprise)。
如果我们观察到了一个不常见的事情发生显然惊讶度高,获得信息量大,极端的如果我们知道一个事件百分百发生那么我们没有任何信息获得。
我们考虑与概率分布p(x)相关联的h(x),表示观测到x值时的信息量,当我们认为x,y无关的时候我们可以认为我们同事观测到它们所得到的信息量与分别观测到它们的信息量相同。对应到p(x),p(y)
h(x,y) = h(x) + h(y) ó p(x,y) = p(x)p(y)
这个关系暗示我们h(x)是对应p(x)的取log
Log的底数是随意的,这里取2,这意味着信息量用bit来度量。
考虑一个发送方希望传输随机变量的值到接收方,那么平均而言传递的信息量就是:
假如一个随机变量x,有8种状态且每种等可能则H[X]=3,如果是(1/2,1/4,1/8,1/16,1/64,1/64,1/64,1/64),则计算得H[X]=2,不均匀分布整体信息量少,3可以表示我们用3个bit表示,如果有的状态概率小我们可以分配较长的编码,对于概率大的分配较短的编码,从而获得最短的平均编码,huffman编码的原理就是基于信息量。
书中提到信息量的另一种物理解释disorder程度,即考虑N各相同的问题分配到一系列的桶里,每个桶有![]() 个,的概率,如果取log再除以N,当N趋向无穷证明等同上面公式。
个,的概率,如果取log再除以N,当N趋向无穷证明等同上面公式。
推广到连续变量
后面用自然对数,思路类似离散连续情况下积分证明见p52,得到下面公式
那么对于高斯分布,利用上式推到可得
于是方差![]() 越大即高斯分布对应的高度越低分布越均匀则信息量越大。
越大即高斯分布对应的高度越低分布越均匀则信息量越大。
高的信息量对应平缓的boring分布,低的信息量对应多变化的(peaks and valledys)分布
条件信息量(conditional entropy)
考虑联合概率分布![]() ,如果我们已经知道了x,那么另外的确定y的信息量就变成了
,如果我们已经知道了x,那么另外的确定y的信息量就变成了![]() ,那么平均情况下另外的(additional)信息量就是:
,那么平均情况下另外的(additional)信息量就是:
可以由此得出:
即观测x的平均信息量加上知道x后观测y的评价信息量就是同时观测到x,y的平均信息。
对应
另外由
考虑离散的情况
一个离散的例子:
![]() //math,yes 1/4, history,no 1/4, cs,yes 1/4, math,no 1/4
//math,yes 1/4, history,no 1/4, cs,yes 1/4, math,no 1/4
相对信息量,互信息(relative entropy, mutual information)
回到随机变量传输问题,假设传输中我们不知道具体![]() 分布情况(unknown),我们用一个已知的分布
分布情况(unknown),我们用一个已知的分布![]() ,来模拟它,那么在这种情况下如果我们利用
,来模拟它,那么在这种情况下如果我们利用![]() 尽可能高效的编码,那么我们平均需要多少额外的信息量来描述x呢。这称为相对熵,或者kl divergence。
尽可能高效的编码,那么我们平均需要多少额外的信息量来描述x呢。这称为相对熵,或者kl divergence。
利用凸函数的不等式性质(也利用了离散求和推广到连续积分)可以证明
因此KL表征了两个分布之间的关系,a measure of dissimilariy of p and q表示两个分布不相同的程度。(感觉这个公式也表明H[X]得到的编码长度是最优的其他编码长度只能更长。)
Mutal info:
考虑如果两个随机变量无关,![]() ,我们可以利用
,我们可以利用![]() 的值来表示p(x),p(y)的相关程度,如果是0则它们无关,KL值越大则相关程度越高。
的值来表示p(x),p(y)的相关程度,如果是0则它们无关,KL值越大则相关程度越高。
TODO(mutal info and correlation ?correlation=0只表示线性不相关是不是就是这个区别?)
![]() 即x,y无关,也即观测到y的情况下观测x的信息量等于直接观测到x的信息量(y不提供额外的信息帮助),
即x,y无关,也即观测到y的情况下观测x的信息量等于直接观测到x的信息量(y不提供额外的信息帮助),
这种情况H[x]=H[x|y]
互信息Mutual information的具体应用
1. 特征选取: (本部分来源<<信息检索导论>>第13章 文本分类和朴素贝叶斯)
对于文本分类应用,如果考虑所有的词汇都作为特征训练,那么可能数据量太大了,而且不具代表性的词汇会作为噪音影响分类精确程度。那么怎么选取一部分有代表性的特征词呢?比如对于类别c,选取k个词作为特征,比如类别“china”-> china,Chinese,Beijing,yuan,shanghai,hong,kong,xinhua…。书中介绍了两种方案,互信息和卡方检验(关于卡方检验)这里仅介绍前者。
思路是利用互信息来表征一个词包含多少表征这个类别的信息量,我们现在训练集合中有的信息只是每个文本里有哪些词,每个文本属于哪个类。c
如果一个词在整个文本集合collection中的分布和在这个类别中的分布是相同的,那么我们认为互信息量为0,相反的互信息为最大,如果一个词在某个文本中出现当且仅当这个文本在这个类别中出现。
举个例子:假设有个4个doc: C1,C2,B1,B2,前2个是C类,后2个非C类
假如case1:
词 c++ 在并且只在C1,B1中出现,那么c++和C类的互信息量为0,
而如果case2:
c++在并且只在C1,C2中出现那么c++与C类达到最大互信息量1(![]() ,两种状态H[X]最大是1)。
,两种状态H[X]最大是1)。
如果case3:
c++在且只在C1中出现。那么互信息量是介于0-1中间的一个值。
互信息具体定义如下:
按照最大似然概率,上面公式可以表示如下,其中N表示所有文本的数目,![]() 表示包含词t并且不属于类别C的文本数目。
表示包含词t并且不属于类别C的文本数目。
对于上面的例子
case1:
case2:
个人认为上面log里面出现了0,可以平滑处理或者假定log里出现0值就是0,因为
n->0取极限的话nlogn=0也可以按照下面计算
I[U]=1 //两种状态均为0.5可能性
I[C|U]=0.5*H[C|U=et=1]+0.5*H[C|U=et=0]=0+0=0 //每个都是只有1个确定状态了
所以I(U;C)=I[U]-I[C|U]=1
case3:
注意如果类似的c++在且并且只在B1中出现
即也是0.5和C类的相关性也是0.5,但是这其实是说明c++的不属于C类的程度!即如果一个doc如果出现了 c++表明它很大概率上不属于C类。(?question有些特定时候会带来问题?副作用词?)
该方法的一个应用推广,我觉得可以在B2C,C2C网站利用用户搜索点击日志,通过利用产品看做doc,搜索词作为term,可以类似的计算term与各个类别的关联程度,从而定位用户搜索类别意图。下一步我会尝试做个试验并贴出效果看看与简单的余弦相似计算比较是否效果更靠谱。(TODO 感觉副作用词应该不太会有影响~)
另外感觉其实tf,idf是有点类似的思想的在本类中倾向出现,在整体中则不是排除那些停用词本类和整体出现的都多。但是上面的互信息量模型没有考虑词在doc中出现次数的因素。
2. 在新词发现中的应用
http://www.cnblogs.com/TtTiCk/archive/2008/06/25/1229480.html
其它资料
l 关于卡方检验
http://www.cnblogs.com/finallyliuyu/archive/2010/09/06/1819643.html
l 关于互信息和相关系数
http://controls.engin.umich.edu/wiki/index.php/Correlation_and_Mutual_Information#Sample_Correlation_Coefficient
![clip_image028[8] clip_image028[8]](http://img.e-com-net.com/image/product/956f0a8862d04b4bbda42d4696f0d85f.jpg)
![clip_image032[7] clip_image032[7]](http://img.e-com-net.com/image/product/35fa2374d71d427291a9e76c4a353c92.jpg)
![clip_image040[4] clip_image040[4]](http://img.e-com-net.com/image/product/24c96c4ebfb64ad5a8a431ba6a0b495d.jpg)
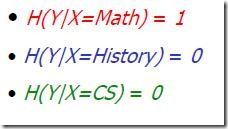

![clip_image056[4] clip_image056[4]](http://img.e-com-net.com/image/product/e02051581e214a37a7a3d430a2aeac2e.png)

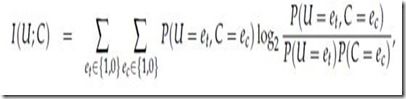

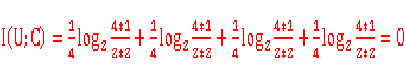
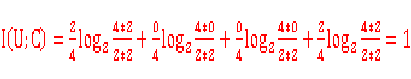
![clip_image002[6] clip_image002[6]](http://img.e-com-net.com/image/product/c2e96f1dc62d4df799b15239ec2b5825.png)
![clip_image004[6] clip_image004[6]](http://img.e-com-net.com/image/product/8ef5ea34d598456abaaad1e6f143c575.png)