基于二分查找实现sqrt函数

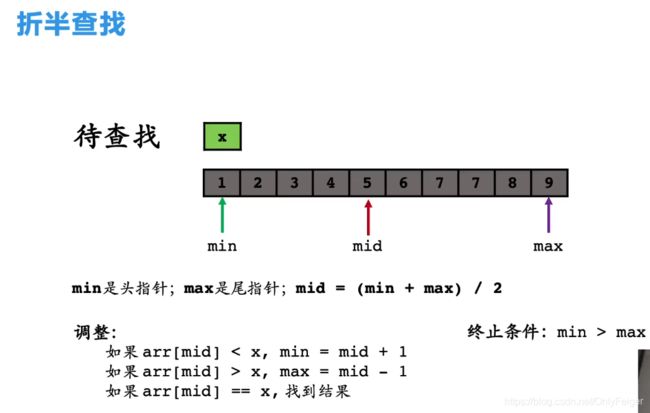
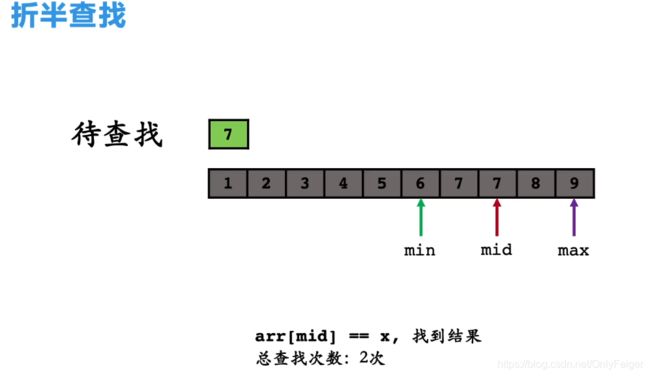
折半查找(又名二分查找)

算法思路:

注意: (当前查找序列必须满足有序序列)
只能确定一个是否存在的值,如过有多个查找值,只会返回其中的一个.

代码实现

int binary_search(int *arr, int x, int n){
     
    int low = 0; high = n -1;//数组长度为n,最后一个元素下标为n-1.
    while (low <= high) {
     
        int mid = (low + high)>>1;//位运算等价于 (low +high)/2;
        if (arr[mid] == x) return mid;
        if (arr[mid] > x) high = mid - 1; 
        if (arr[mid] < x) low = mid + 1;
    }
    return -1;
}

递归版本二分

int binary_search(int *arr, int head, int tail, int value ){
     
    if (head > tail) return -1;
    int mid = (head + tail)>>1;
    if (arr[mid] == value) return mid;
    if (arr[mid] < value) return binary_search(arr,mid+1,tail,value);
    else {
     
        return binary(arr,head,mid-1,value);
    }    
}

进阶(基于二分查找实现开平方根函数)

#include 

int func(int x) {
     
    return x*x;
}
int binary_search(int (*arr)(int), int n, int x){
     
    int head = 1, tail = n, mid;
    while (head <= tail) {
     
        mid = (head + tail) >> 1;
        if (arr(mid) == x) return mid;
        if (arr(mid) < x) head = mid + 1;
        else tail = mid -1;
    }
    return -1;
}

int main() {
     
 	int n;
    while (~scanf("%d", &n)) {
     
        printf("Sqrt(n) = %d\n", binary_search(func, n, n));
    }
    
    return 0;
}

​ 此时我们可以用自己的二分去查找4,9, 16 …的平方根

但是无法查找查找连续问题的平方根

改进程序

#include 
#include 
#define Epsl 1e-6

double func(double x) {
     
        return x*x;
}
double binary_search(double (*arr)(double), double x){
     
   double head = 1, tail = x, mid;
    while (head <= tail) {
     
                mid = (head + tail) / 2.0;
                if (fabs(arr(mid)-x) < Epsl) return mid;
                if (arr(mid) < x) head = mid;
                else tail = mid;
            
    }
        return -1;

}

int main() {
     
        double n;
    while (~scanf("%lf", &n)) {
     
                printf("Sqrt(%g) = %g\n",n, binary_search(func, n));
            
    }
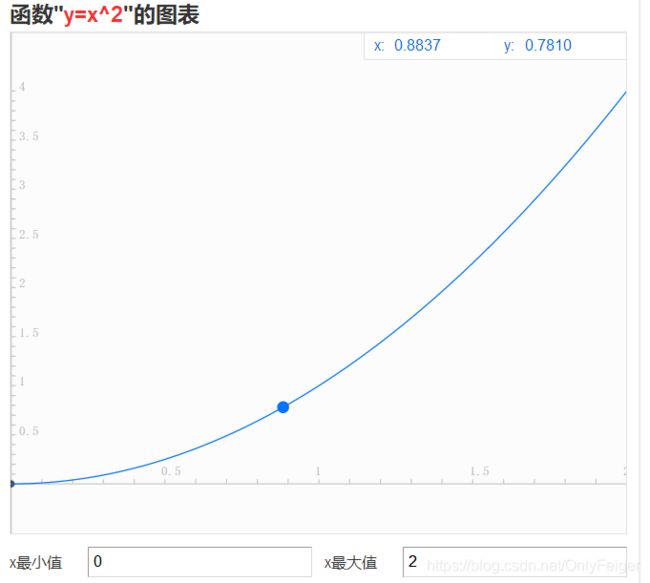
        return 0;

}

---

(思考对于(0,1)区间的数查找不出结果)注意(0,1)区间的数开平方根

小数开平方即使从 0 开始查找 ,结果任然为 -1;在(0,1)区间上x数的增长速度比Y要快,因此X->Y的关系的X大于对应的Y,而在区间(1,+OO),Y大于对应的X,所以在二分后比如(0,0.5)区间内去找X的平方等于0.5是永远找不到的…相反在(1,2)区间内去找X的平方等于2是一定存在的

优化思路:我们可以在查找数小于1时更新查找区间为(0,1)

#include 
#include 
#define Epsl 1e-7

double func(double x) {
     
    return x*x;
}
double binary_search(double (*arr)(double), double x){
     
   double head = 0, tail = x, mid = 0;
    if (x < 1.0) tail = 1.0;
    while (fabs(arr(mid)-x) > Epsl) {
     
        mid = (head + tail) / 2.0;
        if (arr(mid) < x) head = mid;
        else tail = mid;    
    }
    return mid;

}
#undef Epsl
int main() {
     
    double n;
    while (~scanf("%lf", &n)) {
     
    printf("sqrt(%g) = %g\n", n ,sqrt(n));
    printf("my_Sqrt(%g) = %g\n",n, binary_search(func, n));        
    }
    return 0;

}