基于粒子群和改进萤火虫(PGSO)算法的无线传感器网络的覆盖优化

一、理论基础

1、粒子群(PSO)算法

请参考这里。

2、改进萤火虫(GSO)算法

标准萤火虫算法请参考这里。
本文结合无线传感器网络的具体应用场景提出了改进萤火虫算法，具体改进的地方有以下几点：

（1）适应度值

在运用到 WSN 覆盖优化中，每个萤火虫就认为是一个传感器节点。每次迭代仍然由荧光素更新阶段、移动概率更新阶段、位置更新阶段、邻域范围更新阶段组成。传感器节点所具有的荧光素就是代表他周围节点的密集程度，其中，荧光素的大小不仅取决于决策半径内节点的数目，也要考虑节点之间的距离。因此，$J(x_i(t))$计算采用如下公式：$$J(x_i(t))=\sum _{j=1}^k\frac{l_j(t)}{d_{ij}(t)}\text{\hspace{1em}(1)}$$其中，$j\in N_i(t)=\{j:d_{ij}(t)<r_d^j(t),||x_j(t)-x_i(t)||>0\}$，表示节点$i$的邻居节点集合，$d_{ij}$表示节点$i$和节点$j$之间的欧氏距离，$r_d^j(t)$为算法第$t$次迭代下节点$j$的决策半径。

（2）移动概率

在概率计算阶段，为防止荧光素过界，同时避免概率计算负值的产生，本文采用下式来计算移动概率：$$p=\frac{|l_j(t)-l_i(t)|}{\left|2\sum _{k\in N_i(t)}{l}_k(t)-l_i(t)\right|}\text{\hspace{1em}(2)}$$

（3）位置更新

在传感器节点移动的阶段，本部分也做了一定的改进。即采用具有荧光素低
的节点远离它决策半径内具有最大荧光素的节点。这样会使具有较大荧光素的节点附近的节点密集分布的状况降低，进而均匀分布局部范围内节点的部署情况。其计算公式如下：$$x_i(t+1)=x_i(t)-s\times \frac{x_j(t)-x_i(t)}{||x_j(t)-x_i(t)||}\text{\hspace{1em}(3)}$$其中，$s$为移动步长，取$s=\sqrt{3}r-d_{ij}$较为合理。文献[2]证明了$d=\sqrt{3}r$是传感器节点之间可以达到无缝覆盖的最佳节点间距离，在本文中它减去两个节点之间的欧式距离得到步长后再经过公式(3)的计算，就可以得到节点$i$和$j$之间的最佳节点距离。

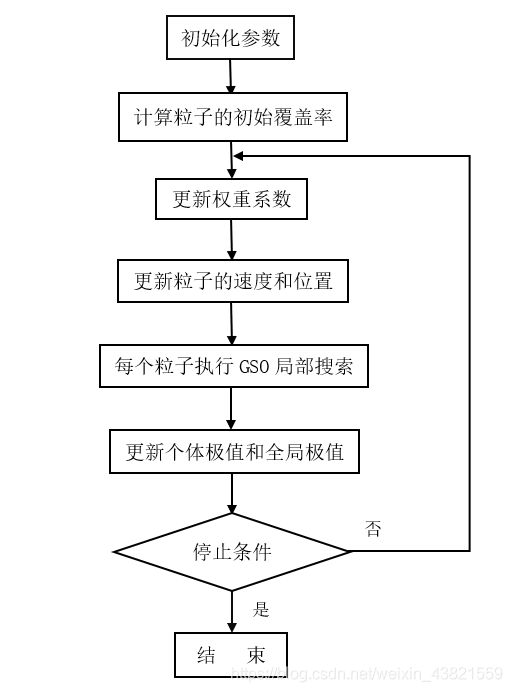
二、算法流程

PGSO算法流程图如图1所示。

图1 PGSO算法流程图

三、MATLAB程序实现

1、参数设置

实验部分参数设置如下：部署区域为$50\times 50$，迭代次数为$500$，传感器感知半径$r_s=5$，通信半径为$r_c=10$，种群规模为$20$，学习因子$c1=c2=2$，惯性权重$wmax=0.9,wmin=0.4$，最大速度设置为$2$，荧光素初始浓度$iot0=400$，邻域阈值$n_t=6$，荧光素挥发因子$rho=0.9$，适应度提取比例$gamma=0.1$，邻域变化率$beta=0.58$。
节点数目设置为$35$。

2、计算覆盖率函数

计算覆盖率函数fun.m代码如下：

function z = fun(x, y, L, R, data)
%% 适应度函数：WSN的覆盖率
% input：
% x        圆心横坐标
% y        圆心纵坐标
% L        区域边长
% R        通信半径
% data     离散粒度
% output:
% z        覆盖率
N = length(x);                  % 节点总个数
[m, n] = meshgrid(1:data:L);    % 离散化区域内的点
[row, col] = size(m);
for i = 1:N
    D = sqrt((m-x(i)).^2+(n-y(i)).^2);  % 计算坐标点到圆心的距离
    [m0, n0] = find(D <= R);            % 检测出圆覆盖点的坐标
    Ind = (m0-1).*col+n0;               % 坐标与索引转化
    M(Ind) = 1;                         % 改变覆盖状态
end
scale = sum(M(1:end))/(row*col);        % 计算覆盖比例
z = scale;

3、改进GSO适应度函数

改进萤火虫算法适应度函数J.m代码如下：

function Jx = J(ioti, rdi, gaddress, d)
%% 改进萤火虫算法适应度值
n = size(gaddress, 1);  % 节点个数
Jx = zeros(n, 1);       % 改进的适应度值
% 计算邻居节点
for i = 1:n
    for j = 1:n
        if j ~= i && d(i, j) < rdi(j)
            Jx(i) = Jx(i) + ioti(j)/d(i, j);
        end   
    end
end

4、主函数

%% 清空环境变量
clc
clear
%% 网络参数
L = 50;              % 区域边长
n = 35;              % 节点个数
rc = 10;             % 通信半径
rs = 5;              % 感知半径
data = 1;            % 离散粒度
%% PGSO参数
maxgen = 500;        % 迭代次数
% PSO参数
sizepop = 20;        % 粒子规模
Wmax = 0.9;
Wmin = 0.5;
c1 = 2;              % 社会认知参数
c2 = 2;              % 自我认知参数
Vmax = 2;            % 最大速度
Vmin = -2;           % 最小速度
popmax = 50;         % 位置最大值
popmin = 0;          % 位置最小值
gbest = zeros(sizepop, 2);   % 最优解
% GSO参数
rho = 0.9;             % 荧光素挥发因子
gamma = 0.1;           % 适应度提取比例
beta = 0.58;           % 邻域变化率
nt = 6;                % 邻域阀值(邻域萤火虫数)
iot0 = 400;            % 荧光素初始浓度
ioti = zeros(n, 1);    % 分配荧光素存放空间
rdi = zeros(n, 1);     % 分配萤火虫决策半径存放空间
gaddress = zeros(n, 2);  % 记录每个节点的位置

%% 随机生成群体位置、速度和对应的适应度值
empty_pop.Position = [];
empty_pop.V = [];
pop = repmat(empty_pop, sizepop, 1);
for i=1:sizepop
    pop(i).Position = rand(n, 2).*[L, L];  % 初始种群位置
    pop(i).V = rands(n, 2)*2;              % 初始化速度
    fitness(i) = fun(pop(i).Position(:, 1), pop(i).Position(:, 2), L, rs, data);      % 粒子群的适应度
end
[bestfitness, bestindex] = max(fitness);
gbest = pop(bestindex).Position;  % 群体最优极值
pbest = pop;                      % 个体最优极值
fitnessgbest = bestfitness;       % 种群最优适应度值
fitnesspbest = fitness;           % 个体最优适应度值
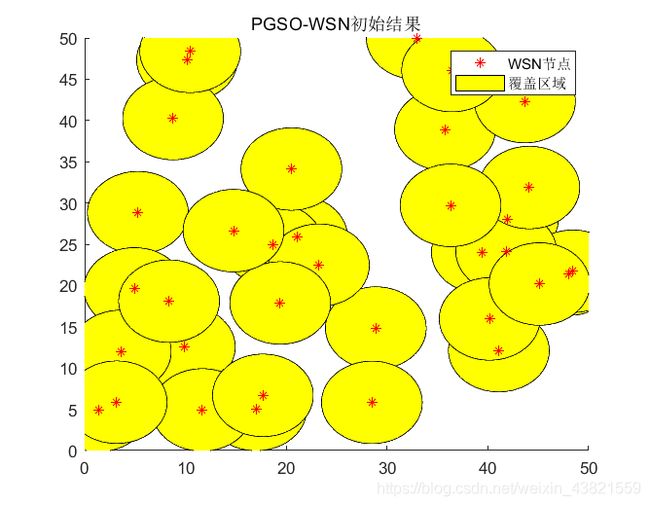
%% 初始结果显示
disp('初始位置：' );
disp([num2str(gbest)]);
disp(['初始覆盖率：', num2str(fitnessgbest)]);
% 初始覆盖图
figure
for i = 1:n
    axis([0 L 0 L]);            % 限制坐标范围
    x = gbest(:, 1);
    y = gbest(:, 2);
    sita = 0:pi/100:2*pi;   % 角度[0, 2*pi]
    hold on;
    p2 = fill(x(i)+rs*cos(sita), y(i)+rs*sin(sita), 'y');
end
p1 = plot(gbest(:, 1), gbest(:, 2), 'r*');
legend([p1, p2], {
     'WSN节点', '覆盖区域'});
title 'PGSO-WSN初始结果';
%% 迭代寻优
for gen = 1:maxgen
    W = Wmax-((Wmax-Wmin)/maxgen)*gen;
    for j = 1:sizepop
        j1 = j;
        %%%%%%%%%%%%%%%PSO搜索%%%%%%%%%%%%%%%%
        %% 速度更新
        pop(j).V = W*pop(j).V + c1*rand*(pbest(j).Position - pop(j).Position) + c2*rand*(gbest - pop(j).Position);
        % 边界处理
        pop(j).V = max(pop(j).V, Vmin);
        pop(j).V = min(pop(j).V, Vmax);
        %% 位置更新
        pop(j).Position = pop(j).Position+pop(j).V;
        % 边界处理
        pop(j).Position = max(pop(j).Position, popmin);
        pop(j).Position = min(pop(j).Position, popmax);
        %%%%%%%%%%%%%GSO局部搜索%%%%%%%%%%%%%
        % 初始化荧光素浓度
        ioti(:, 1) = iot0;
        % 初始化决策半径
        rdi(:, 1) = rc;
        % 记录每个节点的位置
        for k = 1:n
            gaddress(k, :) = pop(j1).Position(k, :);
        end
        d = zeros(n, n);          % 各节点间距离
        % 计算各节点之间的距离
        for i = 1:n-1
            for j = i+1:n
                d(i, j) = sqrt(sum((gaddress(i, :)-gaddress(j, :)).^2));
                d(j, i) = d(i, j);
            end
        end
        % 更新荧光素浓度
        ioti = (1-rho)*ioti+gamma*J(ioti, rdi, gaddress, d);
        % 各萤火虫移动过程开始
        for i = 1:n
            % 决策半径内找更优点
            Nit = [];                 % 存放萤火虫序号
            for j = 1:n
                if norm(gaddress(j, :)-gaddress(i, :)) < rdi(i) && ioti(i, 1) < ioti(j, 1)
                    Nit(numel(Nit)+1) = j;
                end
            end
            % 找下一步移动的点开始
            if ~isempty(Nit)
                Nitioti = ioti(Nit, 1);          % 选出Nit荧光素
                SumNitioti = sum(Nitioti);       % Nit荧光素和
                Molecular = Nitioti-ioti(i, 1);          % 分子
                Denominator = 2*SumNitioti-ioti(i, 1);   % 分母
                Pij = abs(Molecular./Denominator);  % 计算Nit各元素被选择概率
                Pij = cumsum(Pij);                  % 累计
                Pij = Pij./Pij(end);                                 % 归一化
                Pos = find(rand < Pij);             % 确定位置
                j = Nit(Pos(1));                                     % 确定j的位置
                % 萤火虫i向j移动一小步
                s = rs*sqrt(3)-d(i, j);             % 步长
                gaddress(i, :) = gaddress(i, :)-s*(gaddress(j, :)-gaddress(i, :))/norm(gaddress(j, :)-gaddress(i, :));
                % 边界处理(限制范围)
                gaddress(i, :) = min(gaddress(i, :), popmax);
                gaddress(i, :) = max(gaddress(i, :), popmin);
                % 更新决策半径
                rdi(i) = rdi(i)+beta*(nt-length(Nit));
                if rdi(i) < 0
                    rdi(i) = 0;
                end
                if rdi(i) > rs
                    rdi(i) = rs;
                end
                % 更新节点位置
                pop(j1).Position(i, :) =  gaddress(i, :);
            end
        end
        %% 适应度值更新
        fitness(j1) = fun(pop(j1).Position(:, 1), pop(j1).Position(:, 2), L, rs, data);
    end
    %% 个体和群体极值更新
    for j = 1:sizepop
        % 个体极值更新
        if fitness(j) > fitnesspbest(j)
            pbest(j).Position = pop(j).Position;
            fitnesspbest(j) = fitness(j);
        end
        % 群体极值更新
        if fitness(j) > fitnessgbest
            gbest = pop(j).Position;
            fitnessgbest = fitness(j);
        end
    end
    %% 每一代群体最优值存入zz数组
    zz(gen) = fitnessgbest;
end
%% 结果显示
disp('最优位置：' );
disp([num2str(gbest)]);
disp(['最优覆盖率：', num2str(zz(end))]);
%% 绘图
figure;
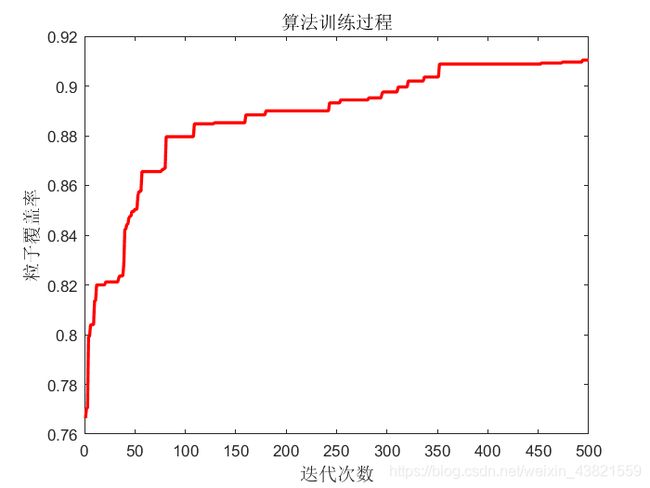
plot(zz, 'r', 'lineWidth', 2);          %  画出迭代图
title('算法训练过程', 'fontsize', 12);
xlabel('迭代次数', 'fontsize', 12);
ylabel('粒子覆盖率', 'fontsize', 12);
figure
for i = 1:n
    axis([0 L 0 L]);            % 限制坐标范围
    x = gbest(:, 1);
    y = gbest(:, 2);
    sita = 0:pi/100:2*pi;   % 角度[0, 2*pi]
    hold on;
    p2 = fill(x(i)+rs*cos(sita), y(i)+rs*sin(sita), 'g');
end
p1 = plot(gbest(:, 1), gbest(:, 2), 'r*');
legend([p1, p2], {
     'WSN节点', '覆盖区域'});
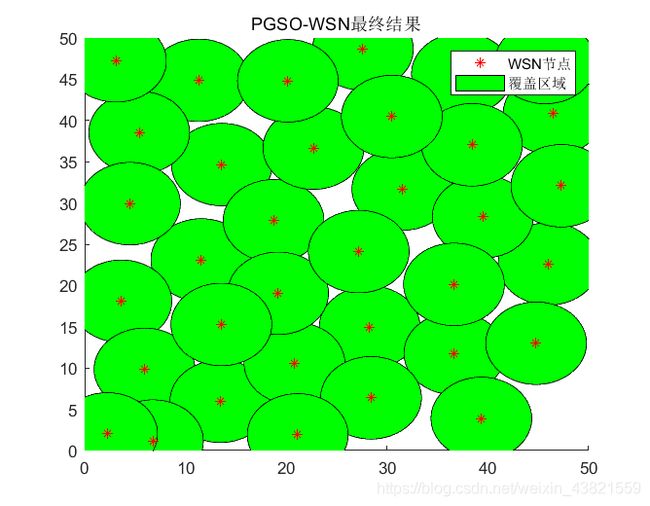
title 'PGSO-WSN最终结果';

5、结果分析

初始随机值和最终的最优解如下：

初始位置：
21.0759       25.902
5.27626      28.8253
4.92733      19.5884
9.94047      12.5639
41.9846      28.0161
47.9877      21.3713
39.3994      24.0353
35.7474      38.9131
17.0146      4.98059
11.6609      4.92432
28.8865      14.8362
48.4209      21.7253
41.8234      24.1026
44.1068      31.8759
28.4959      5.83048
 17.683      6.68695
1.35264      4.84874
18.6595      24.9597
3.58379      12.0164
32.9459      49.9723
41.0889      12.1086
10.1586      47.3247
23.2443      22.4604
8.37579      18.1051
36.3014       29.713
3.17772      5.85677
 8.7676      40.2358
40.1753      15.9451
45.1209      20.1792
20.5095      34.1187
43.6749      42.2925
10.4714      48.3743
36.4452      46.0494
19.3994      17.8842
14.7694      26.6455
初始覆盖率：0.6664
最优位置：
28.2739      14.9477
31.5154      31.6836
11.5724      23.0967
13.6099      34.6611
27.6003      48.6516
36.6767      11.7658
46.0225      22.6248
37.4228      45.6376
46.5163      40.8165
18.7423      27.8411
39.4933      28.3142
3.63829      18.0848
  11.32      44.8635
5.93782      9.83762
13.4634      5.96969
20.8136      10.5496
6.77651      1.14224
28.4094      6.39002
5.41421      38.5294
4.49462      29.9181
19.1844      19.0553
3.10731      47.2256
21.1289      1.89513
22.6951      36.6574
39.3538      3.88901
13.5611      15.2828
38.4195      37.0519
2.23423      2.01141
20.1536      44.8054
44.7852      13.0047
45.6873      47.0253
30.4664      40.4794
47.2873      32.0895
36.6349      20.1393
27.1894      24.1156
最优覆盖率：0.9104

对应的覆盖图如图2、图3所示。

图2 PGSO-WSN初始覆盖效果

图3 PSO-WSN最终覆盖效果

覆盖率变化如图4所示。

图4 WSN节点覆盖率变化

四、算法对比

改进GSO、PSO和PGSO的最终覆盖效果如图5、6、7所示。

图5 改进GSO

图6 PSO

图7 PGSO

三种算法的覆盖率进化曲线图如图8所示。

图8 35个节点下改进GSO、PSO和PGSO的覆盖率进化曲线

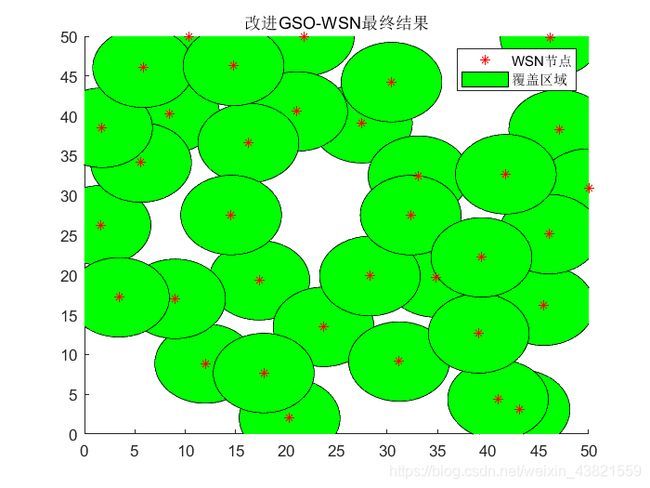
结果表明，所提出的混合算法有更快的收敛速度和更高的覆盖率，提高了寻找全局极值的能力，因此本文提出的混合算法中能够优势互补，达到很好的优化效果，能很好的运用于传感器节点的部署。

五、参考文献

[1] 张谦. 基于群智能算法的无线传感器网络覆盖优化研究[D].湖南大学,2015.
[2] Aziz N, Mohemmed A W, Sagar B S D. Particle swarm optimization and Voronoi diagram for wireless sensor networks coverage optimization. Intelligent and Advanced Systems, 2007. ICIAS 2007. International Conference on. IEEE, 2007:961-965.
[3] ~心升明月~. 基于粒子群优化算法的函数寻优算法. CSDN博客.
[4] ~心升明月~. 基于人工萤火虫优化(GSO)算法的函数寻优算法. CSDN博客.