计算几何总结点、线段、直线
叉积
老是搞不清楚,叉积怎么判断方向的,后来发现就是右手定则的事,看大拇指的方向指向纸面外还是纸面里:
指 向 纸 面 外 ⇔ 叉 积 大 于 0 ⇔ 逆 时 针 \footnotesize 指向纸面外\Leftrightarrow叉积大于0\Leftrightarrow逆时针 指向纸面外⇔叉积大于0⇔逆时针
指 向 纸 面 里 ⇔ 叉 积 小 于 0 ⇔ 顺 时 针 \footnotesize 指向纸面里\Leftrightarrow叉积小于0\Leftrightarrow顺时针 指向纸面里⇔叉积小于0⇔顺时针
x ⃗ × y ⃗ > 0 : \vec{x}\times \vec{y}>0: x×y>0:

x ⃗ × y ⃗ < 0 : \vec{x}\times \vec{y}<0: x×y<0:

应用
x ⃗ × y ⃗ = 0 : x ⃗ 和 y ⃗ 共 线 \vec{x}\times \vec{y}=0: \vec{x}和\vec{y} 共线 x×y=0:x和y共线
判断点与直线的位置关系
题目
TOYS
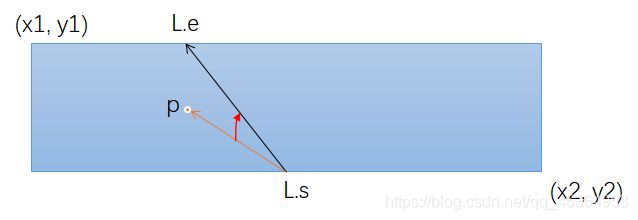
遇到第一个L[i].s P × L[i].s L[i].s < 0 时,i - 1所在的格子玩具个数+1
#include 直线与线段相交
跨立实验:
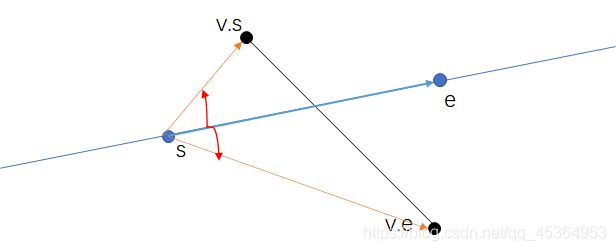
e − s → × v . s − s → \overrightarrow{e-s}\times\overrightarrow{v.s-s} e−s×v.s−s :大于0(小于0),右手定则指向纸面外(内),逆(顺)时针
e − s → × v . s − s → \overrightarrow{e-s}\times\overrightarrow{v.s-s} e−s×v.s−s :小于0(大于0),右手定则指向纸面内(外),顺(逆)时针
e − s → × v . s − s → \overrightarrow{e-s}\times\overrightarrow{v.s-s} e−s×v.s−s与 e − s → × v . e − s → \overrightarrow{e-s}\times\overrightarrow{v.e-s} e−s×v.e−s 异号,所以它们的叉积小于零:
e − s → × v . s − s → ⋅ e − s → × v . e − s → < 0 \overrightarrow{e-s}\times\overrightarrow{v.s-s} \cdot \overrightarrow{e-s}\times\overrightarrow{v.e-s} < 0 e−s×v.s−s⋅e−s×v.e−s<0
题目
Segments
#include 直线与直线相交
1)判断是否平行:叉积判断
2)平行判断是否重合:通过叉积判断一个直线上一点是否在另一个直线上
3)不平行且不重合求交点
题目
Intersecting Lines
#include 线段与线段相交
两次跨立实验判断
题目
The Doors
线段是否是规范相交判断+求最短路
建图:

算法
存储所有墙的端点(除了和周围墙的交点),存储所有墙的线段
选取任意两个不同的端点,判断和所有线段是否存在规范相交,如果不存在则建图,权值为两点之间的距离。
建完图之后跑最短路算法(Floyd或者Dijkstra算法)
#include Pick-up sticks
寻找最上面的木棍编号。
一不小心就会TLE,需要先存储所有线段,然后判断当前线段有没有被之后的线段覆盖,如果覆盖就break,然后记录线段编号用于优化常数
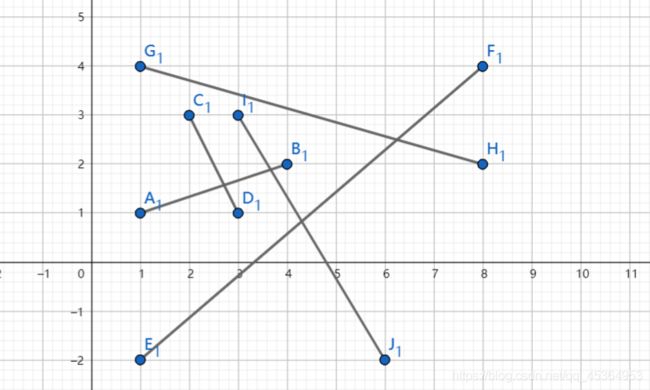
#include 极角排序
确定极点后,利用叉积按照顺时针或逆时针的方向对点进行排序
题目
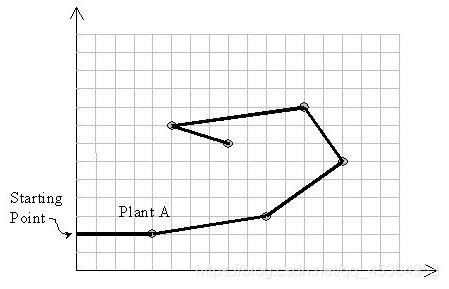
Space Ant
蚂蚁的行动有三个限制:
1)不能右转
2)走过的路会留下红色的标记
3)不会经过之前走过的留下红色标记的路
#include 写在最后的一点感想
可能这是最后一篇关于ACM算法的博客了、明天就是ICPC济南站了,500多个队伍只有200多个牌子。写一点感想吧,还记得大一完的暑假,因为是转专业的,之前从没学过程序设计,想着暑假提前学点东西,看到ACM有暑期训练就加入了,第一次的测试赛,我连一道求和的签到题都写不出来,但是暑期训练结束的比赛好歹可以写三道题了,还拿了一个最快解题奖。后来厚着脸皮加了ACM队,找了wq和yzl组队,不得不说我是真的菜,也很感谢队友不嫌弃。但是训练的经历对于课程的学习帮助很大,短时间内提高一个人的程序设计能力,自学能力,debug能力等等,对于一个人的影响很长远。
打ACM一年半了,第一年太菜了,只有这半年参加了CCPC一次,ICPC一次都打铁了,还有明天的最后一场退役赛,我们能拿牌吗?我不知道(或许我知道,但还是想有希望)。常常怀疑我是不是选错了路,ACM是不是不适合我,也许是沉没成本,也许是学习算法的新知识,也许是和队友一起学习训练的感觉,让我一直坚持到了现在。
最近一直在想没有了ACM我应该做些什么呢?大二和大三上的课余时间大多都用来刷题了,不用刷题之后,我有什么事情可以做呢。搞科研项目?做数学建模?准备考研?准备保研(又很悬)?学习英语?重拾吉他?我不知道,感觉自己一直在忙碌又没有成果,只有看得过去的可怜绩点和没有含金量的几个比赛奖项。
